蘇茹燕, 楊文生②③

(①福建師范大學數(shù)學與統(tǒng)計學院;②福建省分析數(shù)學及應用重點實驗室;③福建省應用數(shù)學中心(福建師范大學),350117,福建省福州市)

0 引 言

在自然界中,獵物會通過不同方式保護自己免于被捕食者獵殺[1,2]. 環(huán)境的異質(zhì)性能為獵物提供避難所,如枯葉蝶會偽裝成枯葉混在落葉中躲避敵害,兔子遇到獵物會伺機找狹小地方隱蔽等. 避難所在一定程度上減少了獵物與捕食者之間的相互作用,增加獵物的數(shù)量[3-6].

具有避難所的生態(tài)種群模型是種群動力學研究的熱點問題之一,目前所研究的具有避難所的生態(tài)種群模型大體上可分為兩類[7-13]. 一類是避難所保護恒定比例的獵物,如Kar等人[14]研究的以下具有避難所的獵物-捕食者模型

(1)

其中x(t),y(t)分別表示獵物種群和捕食者種群的密度,m∈[0,1)表示避難系數(shù),mx表示被避難所保護的獵物數(shù)量. 在此模型中增加避難所的數(shù)量會增加獵物的密度. 另一種類型是避難所保護恒定數(shù)量的獵物,如Mukherjee[15]研究的以下避難所對3種群食物鏈影響的模型

(2)

其中x(t),y(t),z(t)分別表示資源生物量,獵物種群和捕食者種群的密度,m是避難所保護的恒定數(shù)量的獵物. 在此模型中獵物使用的避難所增加了獵物種群的數(shù)量,就捕食者種群而言,當處于平衡水平的獵物密度保持在一定閾值以下時,增加避難所的數(shù)量可以降低捕食者的密度.

然而在自然界中,獵物的避難形式多種多樣,獵物不僅能依靠環(huán)境的異質(zhì)性躲避獵殺還能依靠捕食者對其天敵的恐懼避難,如在“花→蜂鳥→ 藍鴉→老鷹”這條食物鏈中,蜂鳥會選擇在老鷹的勢力范圍內(nèi)筑巢,由于蜂鳥體格小且靈活,老鷹得消耗很多的能量去捕捉蜂鳥,得到的回報卻很少,所以老鷹一般不會捕捉蜂鳥,因此老鷹的勢力范圍對蜂鳥來說就是避難所. 在這種避難形式下中層捕食者的食餌的避難數(shù)量與頂層捕食者的數(shù)量成正比. 基于以上例子,本文研究頂層捕食者對中層捕食者的食餌具有保護作用的食物鏈模型,即

(3)

其中x(t),y(t),z(t)分別代表中層捕食者的食餌,中層捕食者和頂層捕食者的密度,r,k,a1,a2,m,d1,d2,μ,σ均為正數(shù),r表示內(nèi)稟增長率,k表示環(huán)境容納量,a1為中層捕食者對食餌的捕食系數(shù),a2為頂層捕食者對中層捕食者的捕食系數(shù),m為避難系數(shù),d1,d2分別表示中層捕食者和頂層捕食者的死亡率,μ為食餌的生物量到中層捕食者的生物量的轉(zhuǎn)化系數(shù),σ是中層捕食者的生物量到頂層捕食者的生物量的轉(zhuǎn)化系數(shù).

1 平衡點的存在性和局部穩(wěn)定性

本節(jié)討論系統(tǒng)(3)的平衡解的存在性和局部穩(wěn)定性.

首先考慮系統(tǒng)(3)的平衡點的存在性.

(ⅰ)顯然系統(tǒng)(3)存在平凡平衡點(0,0,0).

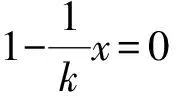
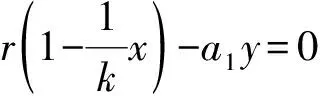
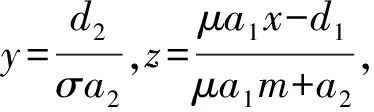
根據(jù)韋達定理,方程的兩根之和與兩根之積分別為

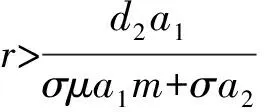
均為正根,其中

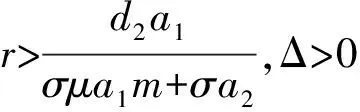
系統(tǒng)(3)的Jacobian矩陣為

(4)

下面證明系統(tǒng)(3)平衡點的局部穩(wěn)定性.

定理2.1 在系統(tǒng)(3)中

(ⅰ)平凡平衡點E0=(0,0,0)是不穩(wěn)定的.

(ⅱ)當系統(tǒng)(3)滿足(H1):d1>μa1k時,邊界平衡點E1=(k,0,0)是局部漸近穩(wěn)定的.

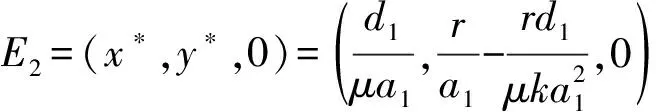
證明(ⅰ)由(4)式知系統(tǒng)(3)在E0處的Jacobian矩陣為

3特征根為λ1=r,λ2=-d1,λ3=-d2,有一個特征根是正根,因此E0是不穩(wěn)定的.

(ⅱ)由(4)式知系統(tǒng)(3)在E1處的Jacobian矩陣為

3特征根為λ1=-r<0,λ2=μa1k-d1,λ3=-d2<0. 由假設條件(H1)得λ2<0,因此E1是局部漸近穩(wěn)定的.

(ⅲ)由(4)式知系統(tǒng)(3)在E2處的Jacobian矩陣為

特征多項式為

其中B,C>0,由假設條件(H2)可得A<0,因此3特征根均有負實部,所以E2是局部漸近穩(wěn)定的.

(ⅳ)由(4)式知系統(tǒng)(3)在E3處的Jacobian矩陣為

特征多項式為

其中

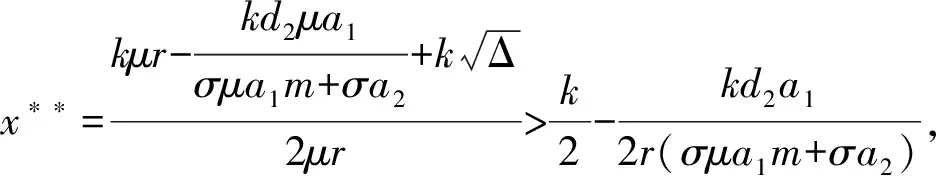
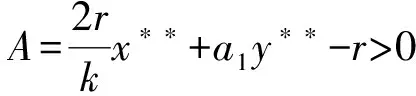
(ⅴ)由(4)式知系統(tǒng)(3)在E4處的Jacobian矩陣為

特征多項式為

其中

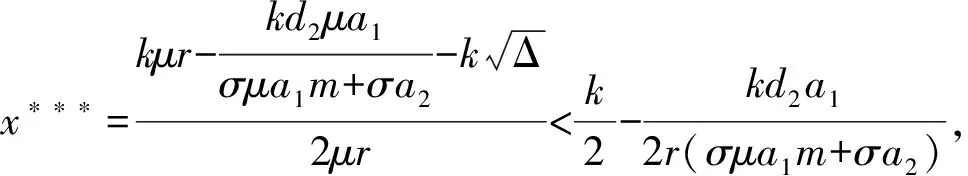
由Routh-Hurwitz條件可知,3特征根不全具有負實部,因此E4是不穩(wěn)定的.

2 平衡點的全局穩(wěn)定性

本節(jié)將通過構(gòu)造的Lyapunov函數(shù)的方法,討論平衡點的全局穩(wěn)定性.

定理3.1

(ⅰ)若系統(tǒng)(3)滿足(H1),則E1是全局漸近穩(wěn)定的.

(ⅱ)若系統(tǒng)(3)滿足(H2)和(H5):d2>σμa1my*+σa2y*時,邊界平衡點E2是全局漸近穩(wěn)定的.

證明(ⅰ)構(gòu)造Lyapunov函數(shù)

(5)

可知,除了E1外,對任意x,y,z>0,有V1>0,對任意的t>0有

(6)

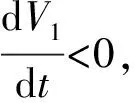
(ⅱ)構(gòu)造Lyapunov函數(shù)

(7)

可知,除了E2外,對任意x,y,z>0,有V2>0. 對任意的t>0有

(8)

(ⅲ)構(gòu)造Lyapunov函數(shù)

(9)

可知,除了E3外,對任意x,y,z>0,有V3>0,對任意的t>0有

(10)

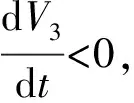
3 數(shù)值模擬

本節(jié)將通過數(shù)值模擬驗證前面得到的理論結(jié)果,并說明避難系數(shù)的變化對物種數(shù)量的影響.

下面先驗證前面的理論結(jié)果,以下數(shù)值模擬的初始條件分別取為:(x(0),y(0),z(0))=(2.5,2,1.5);(2,1.5,1);(1.5,1,0.5).

(ⅰ)當r=2,k=2,a1=2,m=1,μ=0.5,a2=2,d1=4,σ=0.5,d2=1時,系統(tǒng)(3)滿足(H1),存在全局吸引的點E1=(2,0,0) 即y種群和z種群滅絕,x種群存活,如圖1.

(ⅱ)當r=3,k=4,a1=2,m=0.5,μ=0.5,a2=2,d1=2,σ=0.5,d2=1時,系統(tǒng)(3)滿足(H2)和(H5),存在全局吸引的點E2=(2,0.75,0)即z種群滅絕,x種群和y種群穩(wěn)定共存,如圖2.

(ⅲ)當r=2,k=2.5,a1=3,m=1,μ=0.5,a2=2,d1=0.2,σ=0.75,d2=1時,系統(tǒng)(3)滿足(H3),存在局部吸引的點E3=(0.9154,0.6667,0.3352) 即3種群共存,如圖3.

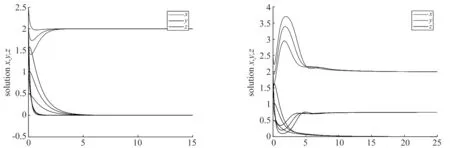
圖1 圖2

圖1：x種群,y種群,z種群如圖中所指.r=2,k=2,a1=2,m=1,μ=0.5,a2=2,d1=4,σ=0.5,d2=1, 初始條件分別為:(x(0),y(0),z(0))=(2.5,2,1.5),(2,1.5,1),(1.5,1,0.5).

圖2：x種群,y種群,z種群如圖中所指.r=3,k=4,a1=2,m=0.5,μ=0.5,a2=2,d1=2,σ=0.5,d2=1,初始條件分別為:(x(0),y(0),z(0))=(2.5,2,1.5),(2,1.5,1),(1.5,1,0.5).

圖3：x種群,y種群,z種群如圖中所指.r=2,k=2.5,a1=3,m=1,μ=0.5,a2=2,d1=0.2,σ=0.75,d2=1,初始條件分別為:(x(0),y(0),z(0))=(2.5,2,1.5),(2,1.5,1),(1.5,1,0.5).

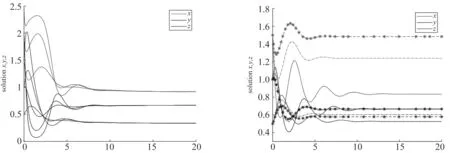
圖3 圖4

下面舉例說明避難所對物種數(shù)量的影響,考慮系統(tǒng)

(11)

以下均取初始條件為：(x(0),y(0),z(0))=(1.5,1,0.5).

(1)當m=0時,系統(tǒng)(11)存在唯一穩(wěn)定的正平衡點(0.8333,0.6667,0.5250),如圖4實線.

(2)當m=0.5時,系統(tǒng)(11)存在唯一穩(wěn)定的正平衡點(1.2390,0.6667,0.6031),如圖4點線.

(3)當m=1時,系統(tǒng)(11)存在唯一穩(wěn)定的正平衡點(1.4834,0.6667,0.5786),如圖4星線.

圖4：x種群,y種群,z種群如圖中所指.m=0時用實線表示,m=0.5 時用點線表示,m=1.5時用星線表示,r=3,k=2.5,a1=3,μ=0.5,a2=2,d1=0.2,σ=0.75,d2=1,(x(0),y(0),z(0))=(1.5,1,0.5).

由圖4可以看出保護力度適當?shù)谋茈y所可以促進獵物的生長且避難系數(shù)變化對x物種的數(shù)量影響較大,當避難系數(shù)增大時,x物種的數(shù)量增加. 對z物種的數(shù)量影響較小,對y物種的最終數(shù)量沒有影響.