Simulation of detection and scattering of sound waves by the lateral line of a fish
V M Adamyan I Y Popov I V Blinova and V V Zavalniuk
1Odessa I.I.Mechnikov National University,Dvoryanskaya Str. 2,Odesa,65082,Ukraine
2ITMO University,Kronverkskiy,49,Saint Petersburg,197101,Russia
3Odessa Military Academy,10 Fontanska Road,Odesa 65009,Ukraine
A solvable model of lateral line of a fish based on a wave equation with additional boundary conditions on a set of isolated points is proposed. Within the framework of this model it is shown that the ratio of pressures on lateral lines on different fish flanks, as well as the cross section of sound scattering on both the lines, strongly depends on angles of incidence of incoming sound waves. The strong angular dependence of the pressure ratio seems to be sufficient for the fish to determine the directions from which the sound is coming.
Keywords: acoustic equation,point self-adjoint perturbations of Laplace operator,scattering,lateral line
1. Introduction
Sound detection capabilities of fishes are mainly based on two sensory systems,the inner ears and small receptor organs called “neuromasts” with sizes in order of 100 μm; in some fish species a gas filled swim bladder is also involved in sound detection.[1,2]There are two types of neuromasts,i.e.,superficial and canal. Superficial neuromasts are scattered on surface of a fish and mainly responsible for detection of surrounding flows,while the canal neuromasts are found in special subdermal canals and percept a pressure gradient of the flow.[3–6]It was shown that fishes are able to localize the direction to the sound source and that the amount of data gathered by the auditory organs is quite sufficient for some species to navigate and hunt in complex dark environments.[7–11]However,full understanding of exact mechanisms of fish sound-based navigation and the details of interactions between fish auditory systems have not been achieved yet.
Sound perception is a multi-stage event that requires four components to occur: a source of vibration, a transmitting medium,a receiving detector,and an interpreting nervous system. Sound energy is carried by motion of the particles that make up the transmitting medium. For inhabitants of aquatic environment,the carrier of sound is water in which they are located. Most fish species and amphibians,among other natural tools,have a special organ known as the lateral line that detects and interprets water vibrations.Visually,as a rule,it represents two dark or light stripes, one on each side of the body trunk of the fish, stretching from the head to the end of the caudal peduncle. In fact, each of the stripes is a single fluid-filled longitudinal canal buried in the skin which contains arrays of equidistant neuromasts (this structure is shown in Fig. 1).The canal is connected to the external environment via secondary fluid-filled tubules that branch off from the main tube and penetrate the skin at regular intervals. Water vibrations are transmitted from the secondary tubules to the canal by sequential compression and expansion of fluid. These vibrations then jiggle the gelatinous domes of hair cells lining the canal.The neuromasts usually alternate with external openings of the canal.
Various aspects of fish hearing(acoustical parameters of lateral line and swim bladder, description of sound receiver,etc.) are described in Refs.[12–19].
In Refs.[20,21]a physical explanation(based on the resonance scattering of incoming sound wave)is given for a mechanism of the detection of a sound source by means of the lateral line organ. In a few words, a system of neuromasts can be approximately considered as a periodic system of identical acoustic resonators with small opening. It was shown that a monochromatic wave falling on such a system can excite edge waves in the vicinity of resonators. The intensity of such a wave drastically depends on the angle between the directions of the incident wave and the lateral line. The fish picks up incoming waves(through neuromasts due to pressure surges)and tunes in to them, changing the orientation of their body in order to achieve the maximum tactile sensation, and thus somehow determines the direction to the sound source.
In this paper, using these considerations as a starting point, we develop a simplified solvable model of the acoustic field in the vicinity of the lateral line, which allows us to compare the overpressure on opposite sides of the fish caused by a distant sound source and to describe the angular distribution of the resulting scattered sound waves.
The proposed approach is based on the perturbation theory for the wave equation in the form of the system of additional boundary conditions at the points of location of neuromasts. In other words, we model the influence of the lateral line on the wave field in the immediate vicinity of the line as a perturbation induced by a system of identical zero-radius potentials[22]sitting in the places of neuromasts. In this way,one can easily supplement recent studies,[23–28]which have used physical instrumentation and mathematical modeling to show that the lateral line of fish is a subtle analyzer of the gradients of the surrounding hydrodynamic fields.
In Section 2, we briefly outline the proposed model and find the explicit expression of Green’s function for the associated Helmholtz equation. Using the obtained expression for Green’s function, in Section 3 we calculate the pressure on each neuromast in the field of a plane monochromatic wave.Meanwhile, considering the neuromasts of the lateral line as a scattering system,we determine the scattering amplitude of a plane monochromatic sound wave incident on this system at an arbitrary angle. Finally, in Section 4, the results obtained are illustrated by calculations based on them,which show that at certain not very low frequencies the ratio of pressures on mirror-symmetric neuromasts from both sides of the fish body,due to phase delay, can vary by many orders of magnitude,depending on the direction of the sound source and the body orientation of the fish. In this case,the resonance dependence of the total and differential scattering cross sections on the incidence angle of the incoming plane monochromatic wave and the orientation of the fish body is also manifested.

Fig. 1. The structure of the lateral line: (a) lateral line position, (b)lateral line structure,(c)neuromast structure.
2. Model description and Green’s function
To construct a model to be solved, we replace small resonators (neuromasts) with point potentials and consider two parallel periodic chains of such potentials as a model of lateral lines on the sides of a fish. The mathematical basis for the development of such models is the theory of extensions of selfadjoint operators(see,e.g.,Refs.[22,29–33]).
To explain the concept of an extension,let us consider the wave equation

for the velocity potentialψ(r,t). Here,Ais the Laplace differential operator?c2Δandcis the speed of sound. To add correctly a single zero-range potential located at the pointr0into Eq.(1)one can start from the standard defined self-adjoint Laplace operator?c2Δ inL2(R3) with the domainH2(R3),whereH2is the Sobolev spaceand we restrict this operator on the set of smooth functions vanishing together with its derivatives at the pointr0=0. The closure of this restricted operator is a symmetric operatorA0with the deficiency indices(1,1). The domain of the corresponding adjoint operatorconsists,for any fixedIms>0,of all the functions in the form of sum
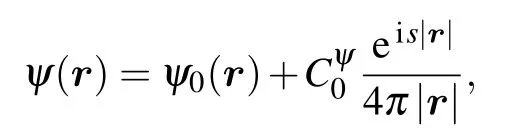
whereψ0∈H2(R3), andis any complex number. The boundary form for anyψ,υfrom the domain ofadmits the representation
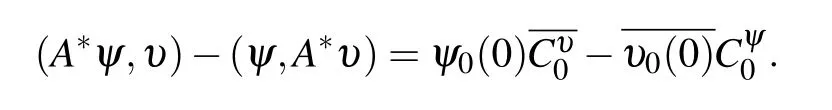
All selfadjoint extensions ofA0are minimal restrictions ofon linear subsets of functions from the domain of,for which the above boundary form equals zero. Each such restriction has the form of an additional linear relation
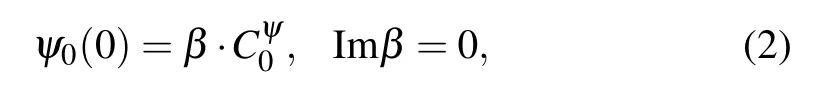
with a certain real parameterβ, ?∞<β ≤∞, which is superimposed on the functions from the domain ofA?0.
The linear relation(2)takes the form of a boundary condition at the origin:
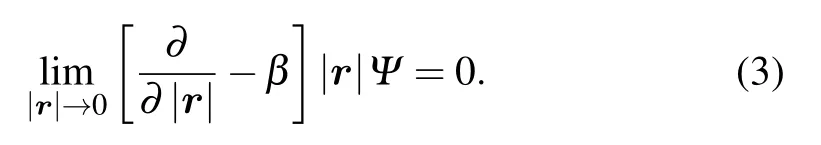
It is worth mentioning that the indicated self-adjoint operators,which are formally defined as Laplace differential operators on the set of functions satisfying the boundary condition (3), in three-dimensional problems legalize the heuristic expressions(see Ref.[22])

From now on we will assume thatβ ≥0,since the selfadjoint extensions ofA0related to the acoustic problems should be non-negative operators.
Further, for simplicity, we will neglect the curvature of the lateral canals on the sides of the fish, and as a model of these canals,together with their openings and neuromasts,wewill consider two parallel chains of equal equidistant potentials of zero radius of the form (3) with the distance between the nearest neighbors in each of the chains equal toa. We will assume that the second chain is shifted relative to the first by the vectorg=g1e1+g2e2,wheree1ande2are unit vectors along the axesXandY, respectively, and that the indicated zero-range potentials are located along the first and second chains at points=na=nae1and=na+g,n= 0,±1,±2,...,±[N/2] (Fig. 2). HereNais the length of each chain and [x] is the integer part ofx. Accepting that the length of the fish body trunk is much greater than the distance between the nearest canal neuromasts and for many fish speciesNreaches and even exceeds 100,[34]in what follows we will assume thatN ?1. It worth mentioning that results of calculations using deduced below explicit asymptotic expression and corresponding numerical calculation cease to differ significantly forN ≥100.
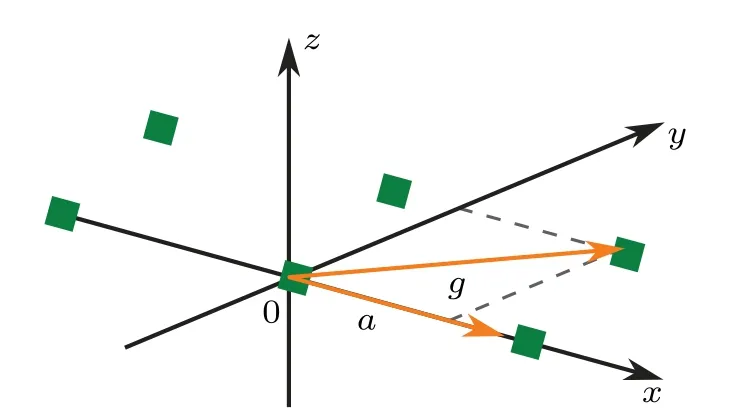
Fig. 2. Schematic of the model setup. Neuromasts (green squares) of the lateral line are on both sides of the fish’s body.
As in the previous case, starting from the selfadjoint Laplacian inL2(R3)with the domainH2(R3),one can restrict this operator on the set of smooth functions vanishing at the indicated points of two chains. The closure of this restricted operator is a symmetric operator with infinite deficiency indices.It has rich family of self-adjoint extensions. To construct a suitable self-adjoint extension,one can take the corresponding adjoint operator. An element from its domain has the following form:

whereψ0belongs to the domain of the initial selfadjoint Laplacian,are some constants,such that the series (4)converges to aL2(R3)function and Ims>0. Choosing the extension corresponding to the sum of the same zerorange potentials,as described above,at pointsna,na+g,n=0,±1,±2,...,that is,the extension determined by the boundary conditions
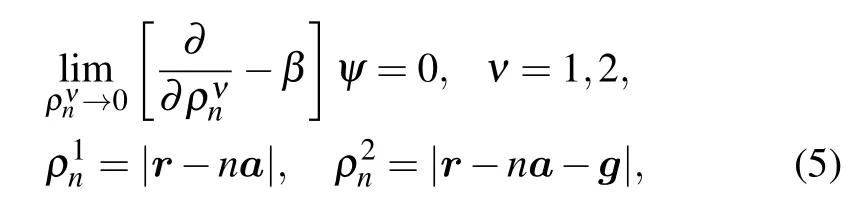
yields a self-adjoint operatorA, as required for the model in question. For simplicity,we set furtherg=ge2.
Green’s function forA(the kernel of the integral operator(A?s2·I)?1,Ims>0, I-unity operator) in general has the form

The system of boundary conditions (5) gives us a sufficient number of equations to uniquely determine the numerical values of the coefficients. At the same time forN ?1,repeating the same considerations that are used in solid state theory to describe vibrational or electronic excitations of crystal structures, one can easily obtain approximate expressions for the same coefficients, the more accurate the moreN. To obtain in this way an explicit expression for Green’s functionG(r,r′,s)we put

Using the boundary conditions (5) one can easily check that the functionssatisfy the following system of algebraic equations:
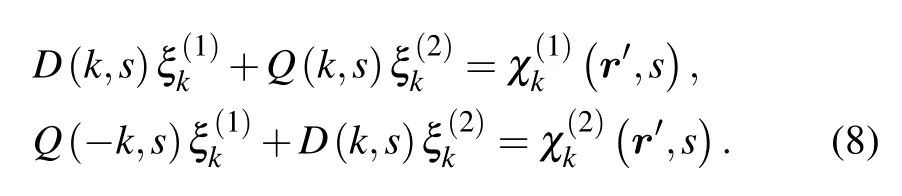
Taking into account expressions (7), Eq. (8) and the inversion formula yields
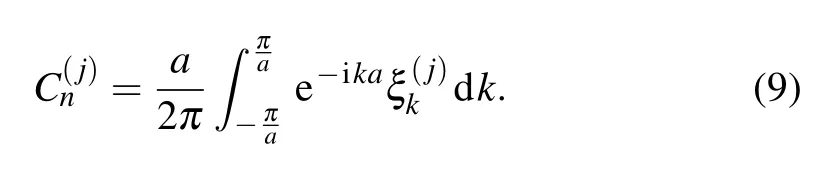
We can conclude that the following version of Krein’s formula for Green’s function forAis valid:
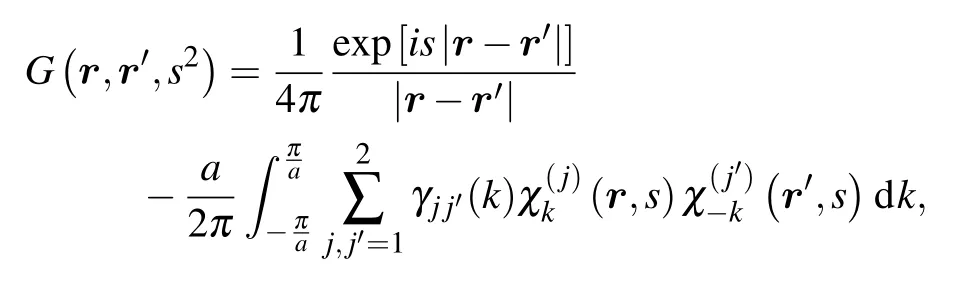
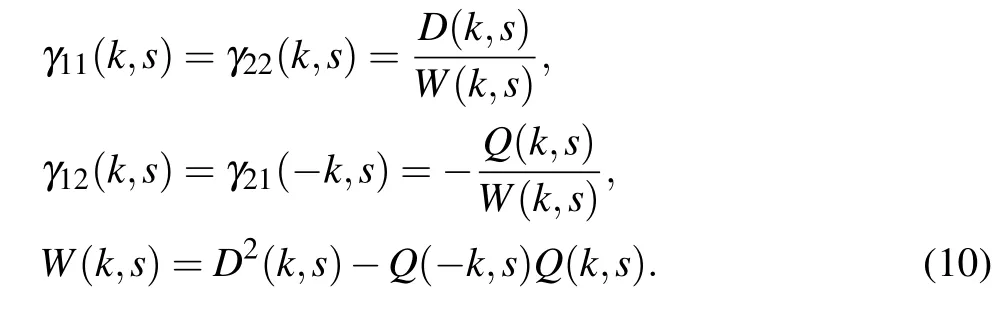
3. Remote source detection and sound scattering
If the complex amplitude of steady-state sound vibrations caused by a point source

at a pointRcreates an excess variable pressurep0e?iωtat a short distancer0, qr0?1 from the source, then at arbitrary pointrthe complex amplitude of the excess pressurep(r)e?iωtwill be determined by the expression
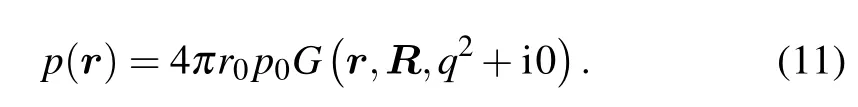
From now on we will assume that the distance from the origin to the remote source reads|R|=R ?Na.
Within the framework of the model under consideration,the expression(11)is singular at the points mimicking neuromasts’ positions on the lateral line. To get around this difficulty, assuming thatr0in(11) is significantly smaller thana,we will define the pressure at pointsn=0,±1,±2,...as the average

Krein’s formula (10) and explicit expressions (7) and (8) for its entries yield
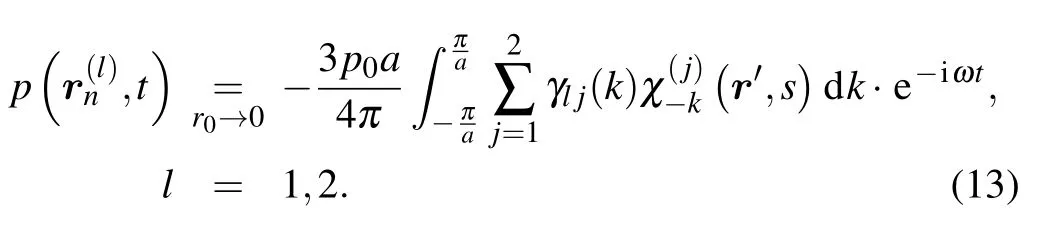
Taking into account that the sound absorption in water increases with frequency, we restrict ourselves also to cases in which the frequency of incoming sound satisfies the condition

Remember that
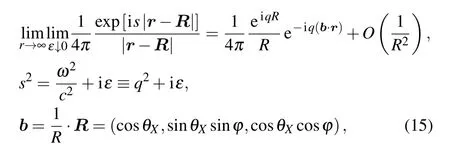
whereθXandφare polar and azimuthal angles, respectively(see Fig.3),and
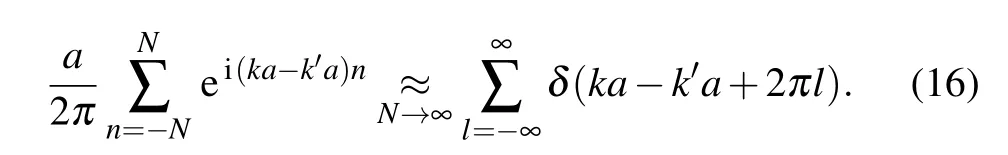
The expressions for excess pressuresP(1)(t) andP(2)(t)on two parallel parts of the lateral line can be deduced from Eq. (13) with the account of the asymptotic expression (15),formula (16) and the restriction (13). Assuming thatR ?L,i.e., the distance between the fish and a remote point source significantly exceeds the length of the lateral line,the expressions forP(1)(t),P(2)(t)can be written in the following form:

These expressions make it possible in principle to determine the direction of the radius vector drawn from the fish to a remote source.
For the scattering of a plane sound wave
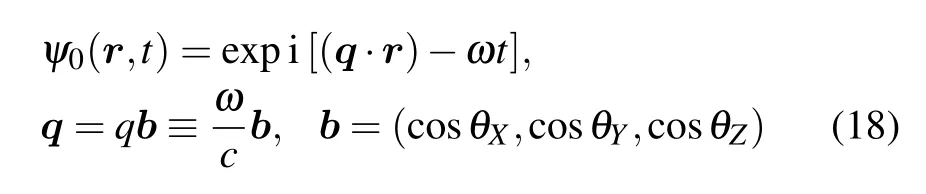
by the considered system of point potentials the corresponding solution of the wave equation (1) is determined according to the Lippmann–Schwinger equation
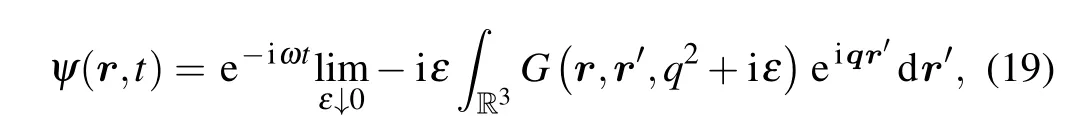
(details can be found in Ref.[35]).
Note that
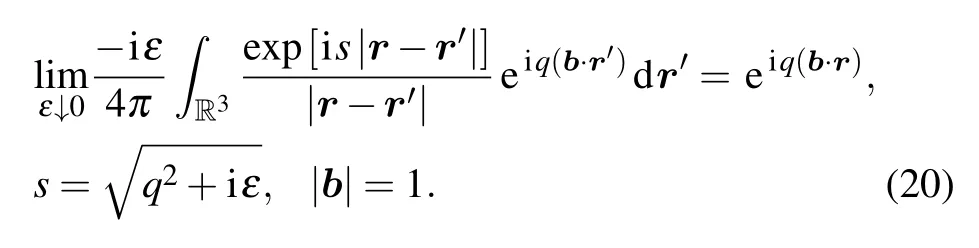
Therefore,referring to the functions in(7),in the limitN →∞we have
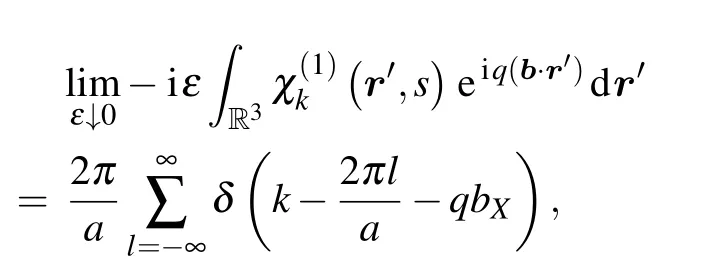
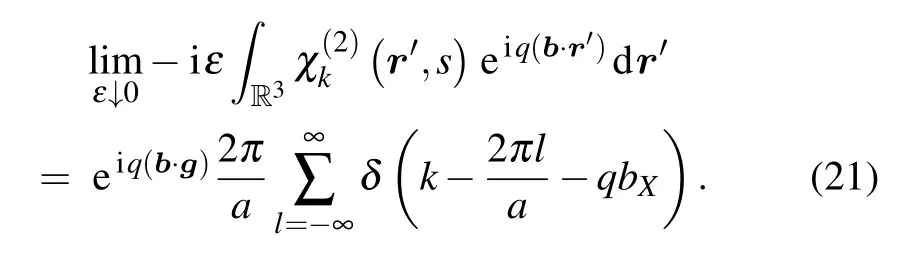
Hence,by virtue of Eqs.(10)and(19)–(21)we have
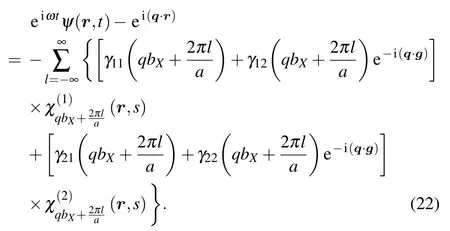
Remembering again the asymptotic expression (15) we also see that
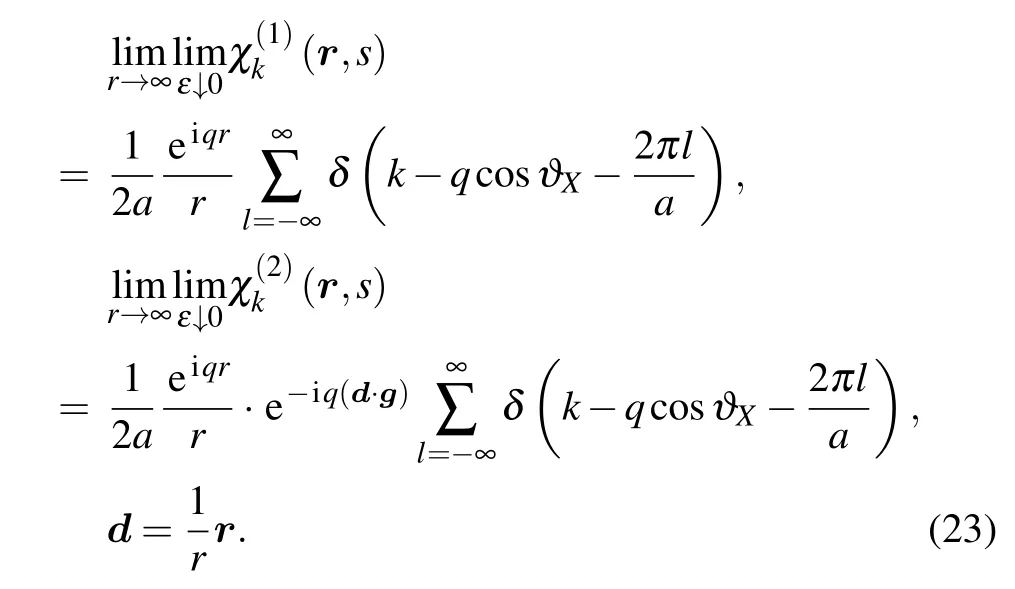
Using relations(22)and(23)we find that the scattering amplitudefω(d,b),
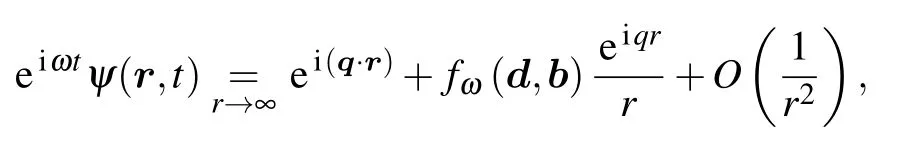
forN ?1 has the form
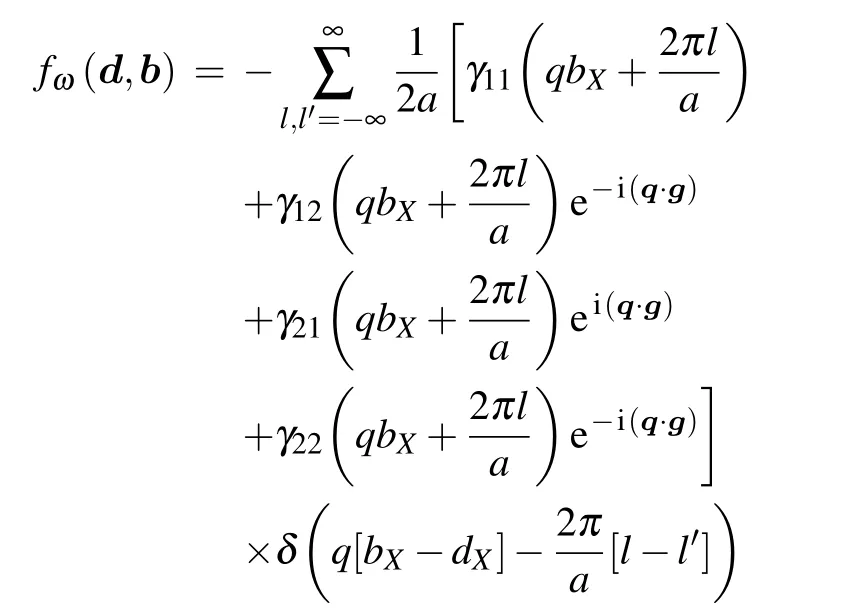
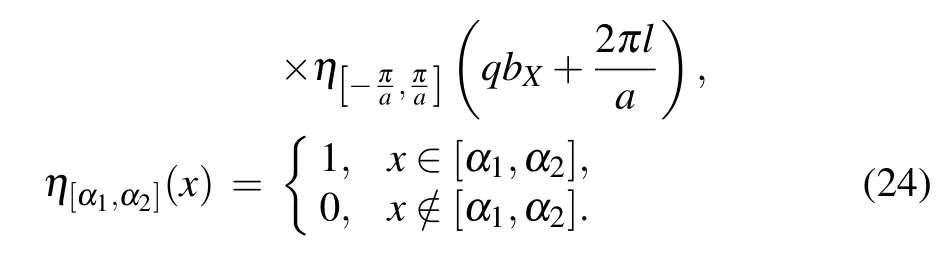
As followed from(24),scattering from the lateral line can be observed only when the projections of the wave vectors of the waves incident on this line and reflected from it satisfy the Bragg-type condition
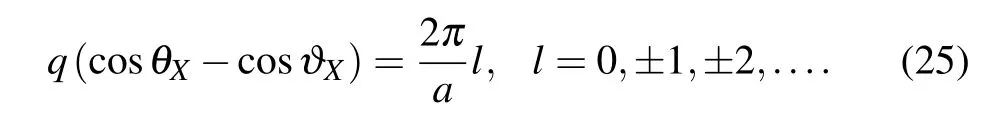
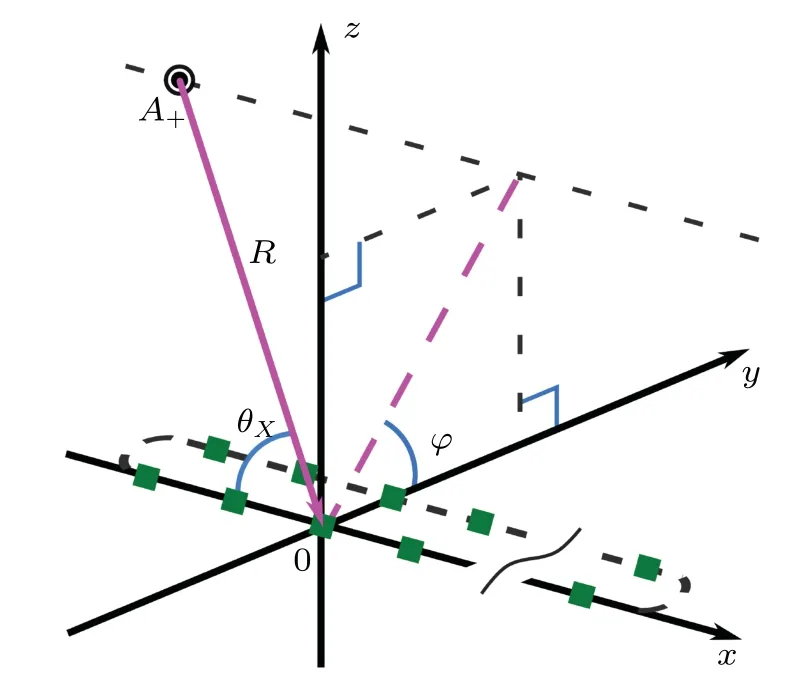
Fig. 3. Angles of incidence of the incoming sound wave on the fish body.
If the sound wavelength is larger than 2a, thenbX=dXand

Thus,for sound wavelengths greater than 2a,that is,if the condition(14)holds,sound scattering will occur while maintaining the projection of the wave vector on the direction parallel to the lateral line.Given the conservation of this component of the wave vector,the scattering amplitude in the plane perpendicular to the lateral line as a function of,angleθXand the scattering angleφin the plane perpendicular to the lateral line,
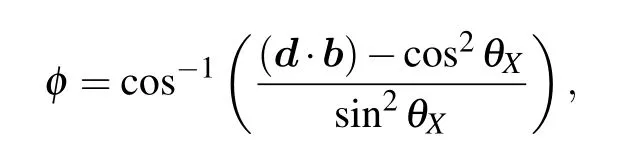
is determined by the expressions
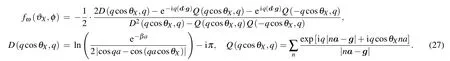
These expressions can be further simplified,given that thex-component of the vectorgis negligibly small or can be neglecteddue to other reasons(for example,ifa ?|g|andqa ?1). In such cases due to the equalityQ(k,s)=Q(?k,s)the expression(27)takes the form
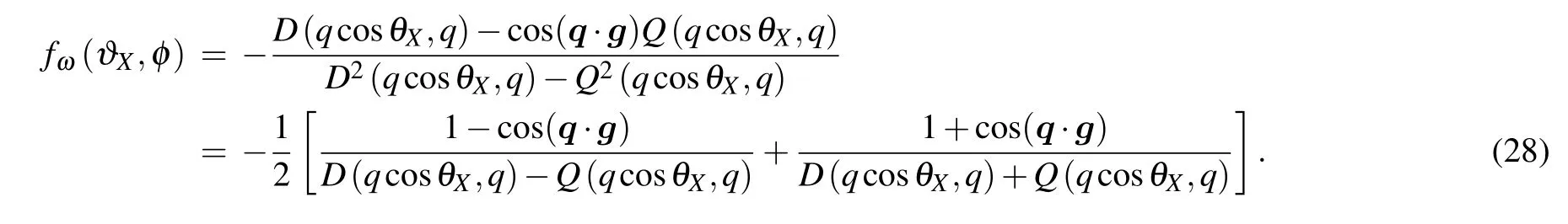
4. Discussion
The starting point for the development of the considered model was the mechanism of a sound detection by the lateral line of fishes proposed in Refs.[20,21],where the corresponding analysis was generally qualitative. In the present paper we develop a quantitative approach, which allows to distinguish the pressures caused by an external source on the lateral lines on the different sides of the fish body trunk and to calculate the differential cross section of sound scattering on the lateral line.
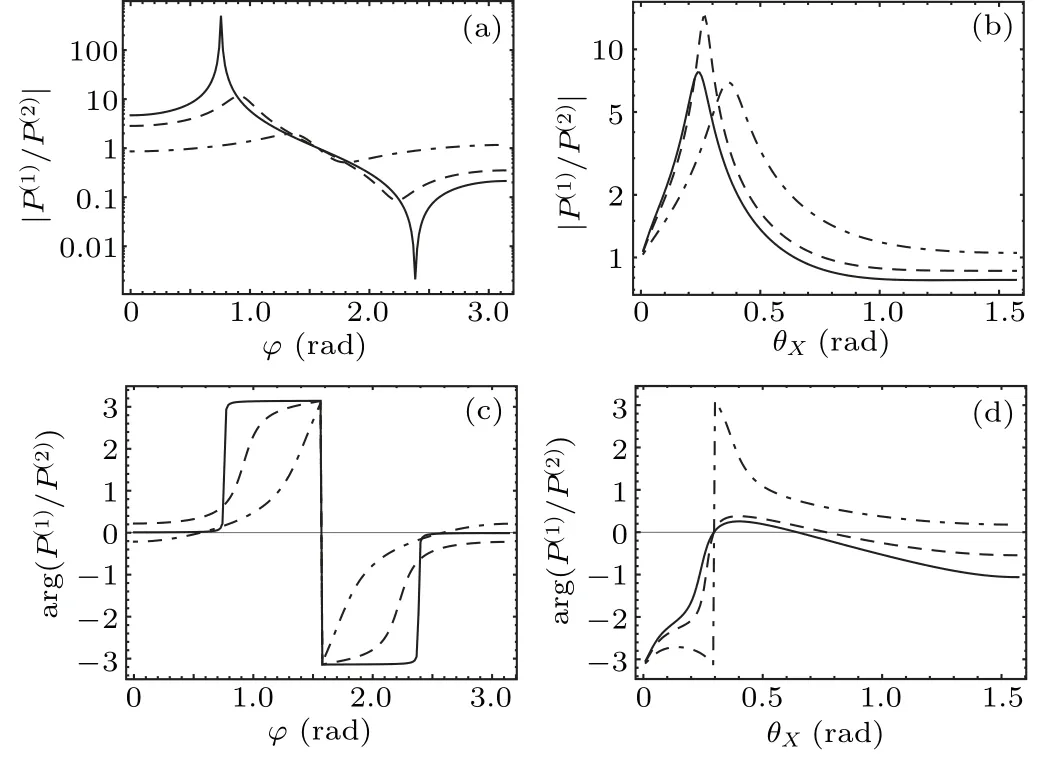
Fig. 4. The ratio of the pressure amplitudes and the phase difference for pressures P(1)(t),P(2)(t)on the flanks of the fish,calculated by formula(17)for the frequency corresponding to qa=π/6:(a)as a function of φ for different values of θX;(b)as a function of θX for different values of φ;(c)argas a function of φ for different values of θX;(d)arg as a function of θX for different values of φ.In images(a)and(c),solid,dashed and dash-dotted lines correspond to , respectively. In images(b)and(d), solid, dashed and dash-dotted lines correspond to φ =0, ,respectively.
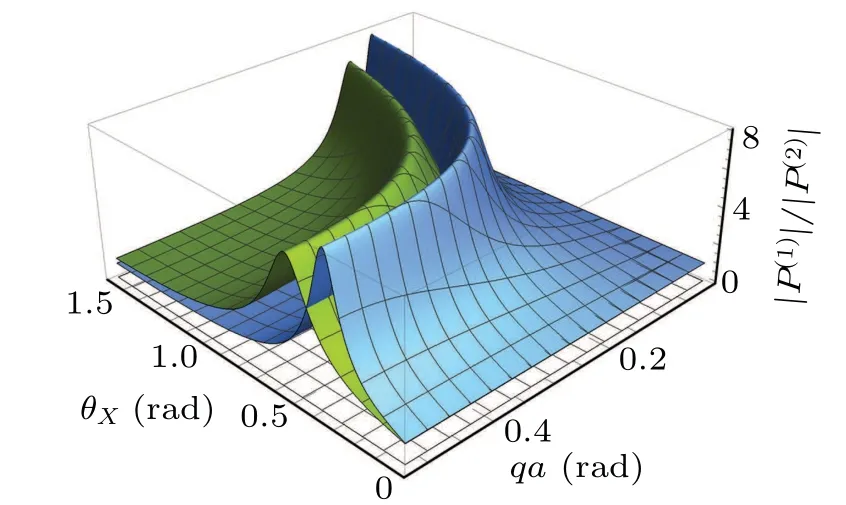
Fig. 5. The ratio for different qa and θX (φ =0 (blue) and φ = (green)).
The expressions obtained for the excess pressures on the lateral line on opposite flanks of the fish caused by a remote point source demonstrate a pronounced dependence of those pressures both on the sound frequency and source position relative to the fish body in terms of the anglesθXandφ(see Figs.4 and 5).
Dependence on the angles becomes stronger with increasing sound frequency and manifests itself strongly for the phase shift and amplitudes quotient for fluctuations of excess pressures on both sides of the lateral line along sides of the fish.
In the case of sound scattering on a lateral line within the framework of the considered model, the projections of wave vectors of the incident and scattered sound waves onto the lateral line,as expected from symmetry considerations,are preserved. Note that in this case the dependence of the scattering amplitude on anglesθXandφbecomes more pronounced with the increasing frequency(Fig.6).
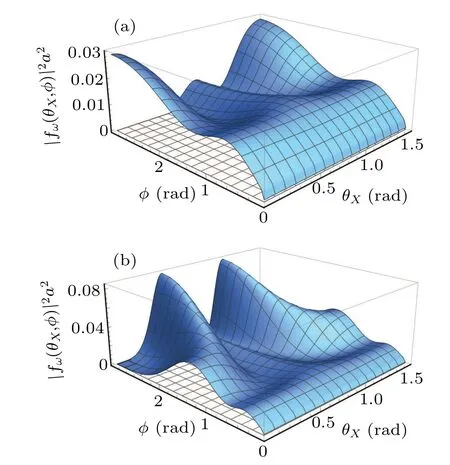
Fig.6. The differential scattering cross section|fω(θX,φ)|2 calculated by formula(28)for the frequency of the sound wave corresponding to qa= (a)and qa= (b).
Of course, due to the excessive sketchiness of the proposed model and insignificant simplifications in the calculations, the results obtained do not reveal the entire functionality of the lateral line of fishes. However, the model can be improved. Instead of point potentials, one can use resonators with a point window approximation(see Refs.[30,31])or point potentials with an internal structure.[36]For fisheswith lateral lines of the “surface” type, Green’s function for free space might be replaced by Green’s function for two halfspaces with different speeds of sound,[37,38]and for fishes with lateral lines of the“cannel type”,i.e.,by Green’s function for three-dimensional space with a potential with periodic internal structure,concentrated on two parallel lines.All these changes make it possible to expand the scope of the model under consideration. However,these improvements are unlikely to substantially change the pronounced binaural effect (see Figs. 4 and 5), which, in our opinion, allow fishes to determine the bearing of sound sources.
Note that even in the present form the model and its results can be useful for the rapidly developing field of the development and application of an artificial later line and different later-line-inspired sensors.[39,40]Such sensors find their use in aeroacoustic measurements,[41]hydrodynamic sensing,[42–45]as a navigational instrument for robotic fishes,[46–49]etc.
Acknowledgements
This work was supported by the Ministry of Education and Science of Ukraine (Grant No. 0115U003208). The authors thank Dr. R.Fricke for useful advice.
- Chinese Physics B的其它文章
- A broadband self-powered UV photodetector of a β-Ga2O3/γ-CuI p-n junction
- High-sensitive terahertz detection by parametric up-conversion using nanosecond pulsed laser
- High efficiency,small size,and large bandwidth vertical interlayer waveguide coupler
- High-fidelity resonant tunneling passage in three-waveguide system
- An analytical model for cross-Kerr nonlinearity in a four-level N-type atomic system with Doppler broadening
- Determine the physical mechanism and source region of beat wave modulation by changing the frequency of high-frequency waves