Xu-Dong Zhang,Sheng-Bang Qian,,4,Er-Gang Zhao,Qi-Jun Zhi,Ai-Jun Dong,and Bin Zhang

1 School of Physics and Electronic Science,Guizhou Normal University,550025 Guiyang,China;astronomy2015@foxmail.com

2 Guizhou Provincial Key Laboratory of Radio Astronomy and Data Processing,Guizhou Normal University,Guiyang 550025 Guiyang,China

3 Yunnan Observatories,Chinese Academy of Sciences(CAS),650216 Kunming,China

4 University of Chinese Academy of Sciences(UCAS),100049 Beijing,China

Received 2021 August 4;revised 2021 November 2;accepted 2021 November 9;published 2022 February 2

Abstract Multi-color light curves of CSS J075415.6+191052 and NW Leo are presented and the photometric solutions suggest that CSS J075415.6+191052 is an A-subtype contact binary with low mass ratio(q=0.178)while NW Leo has a high mass ratio(q=0.707).For CSS J075415.6+191052,the RI light curves show weakening around the left shoulder of the secondary minimum,which indicates that there may be a dark spot on the secondary component.However,the light curves of BV bands are totally symmetric.It is unreasonable if the dark spot is caused by magnetic activity or mass transfer between the two components.Therefore,weakening of the light curves in this contact binary is caused by something else.A possible explanation is mass transferring from the primary component to the common convective envelope through the inner Lagrangian point,and this part of the mass,for some reason,weakens the RI bands of light from the secondary component.O?C analysis of NW Leo reveals a cyclic period change with a modulation period of 4.7 yr,which may be caused by the light travel time effect of a third body.The positions of CSS J075415.6+191052 and NWLeo in the P–J′orb diagram indicate that CSS J075415.6+191052 mainly abides by the angular momentum loss theory while NW Leo is dominated by the thermal relaxation oscillation theory.

Key words:(stars:)binaries:eclipsing–stars:evolution–stars:individual(CSS J075415.6+191052,NW Leo)

1.Introduction

The light curves(LCs)of eclipsing binaries are divided into three types:EA,EB and EW.The time of entry and exit of an eclipse can be found easily in EA-type LCs,in other words,the EA-type LCs do not change continuously.The other two types of LCs both change continuously.EB-type LCs show big differences between the two minima,because the masses of the two components in a binary system are usually different,with the more massive component(primary)being hotter than the less massive one(secondary).However,an EW-type LC exhibits very similar depth between the two minima,which is very special.It means that the two components manifest almost the same effective temperature,even though they have different masses.In addition,many EB-and EW-type LCs display asymmetry[e.g.,LL Com(Hu et al.2019);V599 Aur(Hu et al.2020)].For EB-type LCs,mass transfer between the two components or magnetic activity spots is the explanation for LC asymmetry.But for EW-type LCs,the situation is much more complicated.The special properties of EW-type eclipsing binaries are described by Qian et al.(2017),which indicate that EW-type binaries are well worth investigating.The latest studies have improved the understanding of contact binaries(e.g.,Li et al.2019;Zhang et al.2020a;Zhang&Qian 2020b;Li et al.2020;Qian et al.2020;Latkovi?2021;Li et al.2021),however,the work is far from complete.

According to the Roche geometry,close binaries fall into three categories(Kopal 1955,1959).If neither component fills its Roche lobe then the binary system is called a detached binary,or else if only one component fills its Roche lobe then the binary is called a semi-detached binary.When both components fill their Roche lobes,the binary system is a contact binary.Due to the two components of a late-type contact binary sharing a common convective envelope in which energy transfer happens(Lucy 1968),their effective temperatures are very close even though they have different masses.For this reason,contact binaries usually exhibit EW-type LCs.Moreover,according to the classi fication(Binnendijk 1970),contact binaries are divided into two subtypes.If the primary component is eclipsed at the deeper minimum,then it is an A-subtype contact binary,while a W-subtype one is the opposite.A W-subtype contact binary is very unusual in that the secondary component is hotter than the primary one.The connection among energy-transfer,thermal relaxation oscillation(TRO,Flannery 1976;Lucy 1976)and W-subtype contact binaries has been discussed in a previous paper(Zhang et al.2020a).Liu et al.(2018b)proposed a new mechanism oflong-term period variations for contact binaries,which highlights the role of the common convective envelope in the evolution of contact binaries.Therefore,the effect of the common convective envelope on other properties in contact binaries has to be considered.Mass transfer is not the only process occurring between the two components,and the common convective envelope will also be involved.

In addition,several factors may lead contact binaries to merge,such as the mass ratio (Rasio 1995;Arbutina 2007,2009),the degree of contact(Rasio&Shapiro 1995)and angular momentum loss(AML,van’t Veer 1979;Rahunen 1981;van’t Veer&Maceroni 1989;Stepień&Gazeas 2012).So,it is very important to examine their current evolutionary state.Contact binaries have so many special properties(Qian et al.2017,2020),understanding these properties is important and meaningful.Recently,we devoted systematic research on the special properties of contact binaries.In this study,we take the contact binary CSS J075415.6+191052 as a good example to reveal a new type of LC asymmetry,which was seldom noticed before.In addition,the evolutionary stages of CSS J075415.6+191052 and NW Leo are discussed.

2.Photometric Solutions of CSS J075415.6+191052

CSS J075415.6+191052 was observed on three days(2016 December 29,30 and 2017 January 1)by using the Sino-Thai 70 cm telescope at Lijiang station of Yunnan Observatories.The charge-coupled device(CCD)system was the Andor DW-936N-BV and the filter was the Johnson–Cousin–Bessel system.The coordinates of the comparison star and check star are listed in Table 1.BVRI-four band LCs were obtained(see Figure 1)and the phases were computed with the following linear ephemeris,

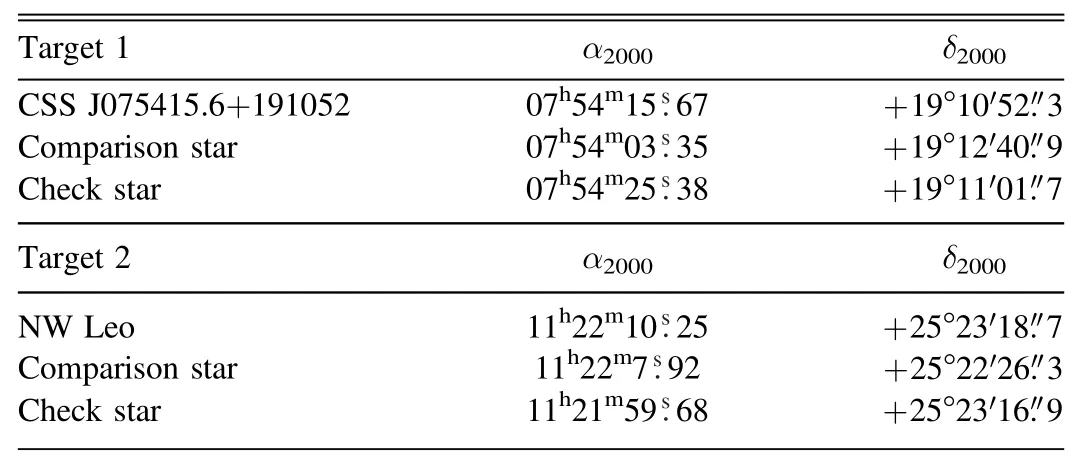
Table 1Coordinates of Targets

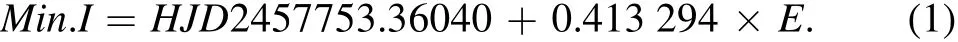
Figure 1.Bottom:Observed BVRI LCs of CSS J075415.6+191052.Top:The magnitude difference between the comparison star and the check star.

Photometric parameters are derived by utilizing the Wilson-Devinney(W-D)code(Wilson&Devinney 1971;Wilson 1979,1990,1994).Thanks to the Large Sky Area Multi-Object Fiber Spectroscopic Telescope(LAMOST,also called the Guoshoujing Telescope), a large number of spectral observation data were provided(Luo et al.2015).The spectral type of F7 is determined,so we set the effective temperature of the primary component asT1=6217 K.The bolometric and bandpass square-root limb-darkening parameters can be derived from van Hamme(1993).Because the temperature is less than 6500 K,the gravity-darkening and bolometric albedo coef ficients were assumed to beg1=g2=0.32(Lucy 1967)andA1=A2=0.5(Rucinski 1969)respectively.

The LCs of CSS J075415.6+191052 are typical EW-type,and Mode 3(contact mode)is applied.During the modeling,the adjustable parameters were orbital inclination(i),effective temperature of star 2(T2),monochromatic relative luminosity of star 1(L1B,L1V,L1R,L1I)and dimensionless potential of star 1(Ω1).Since there is no spectroscopic mass ratio,the mass ratio(q)is determined by comparing a series of solutions with assumed values ofq(called the q-search method).The photometric solutions listed in Table 2 indicate that CSS J075415.6+191052 is an A-subtype contact binary with a very low mass ratio.Theoretical LCs are plotted in Figure 2.

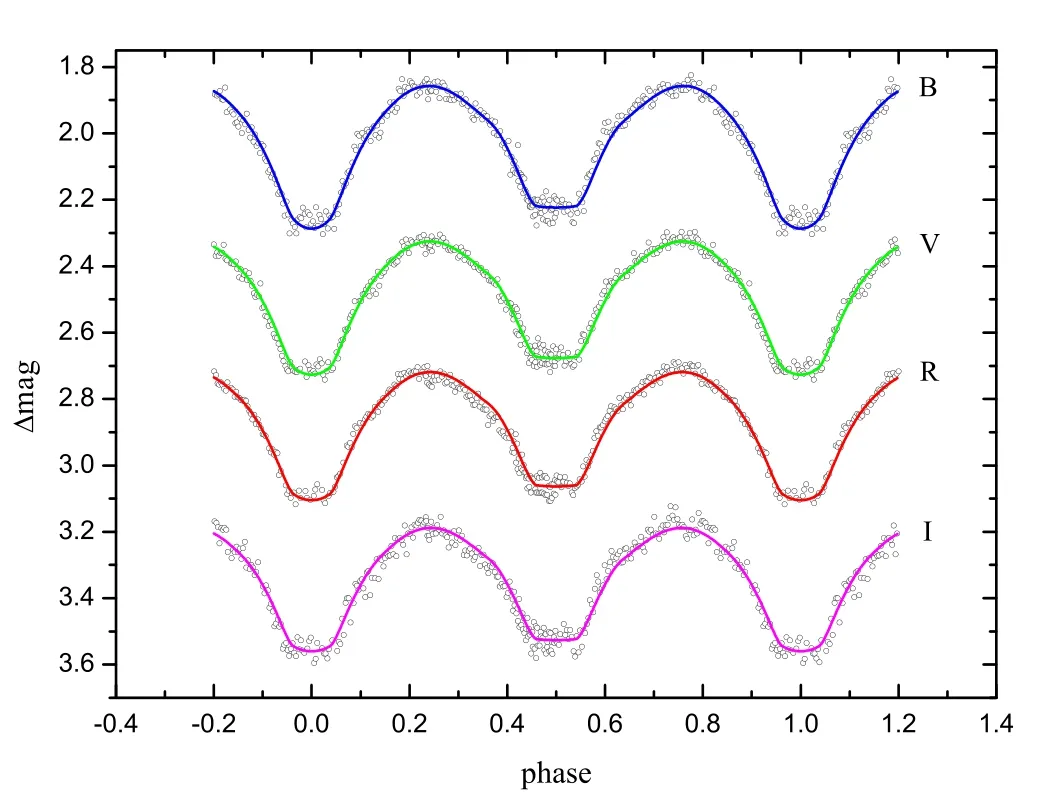
Figure 2.Comparison between observed and theoretical LCs of CSS J075415.6+191052.One can clearly see that the RI bands LCs weaken around phase 0.25–0.5.

Figure 3.LCs of NW Leo.The phases were computed with the old linear ephemeris.

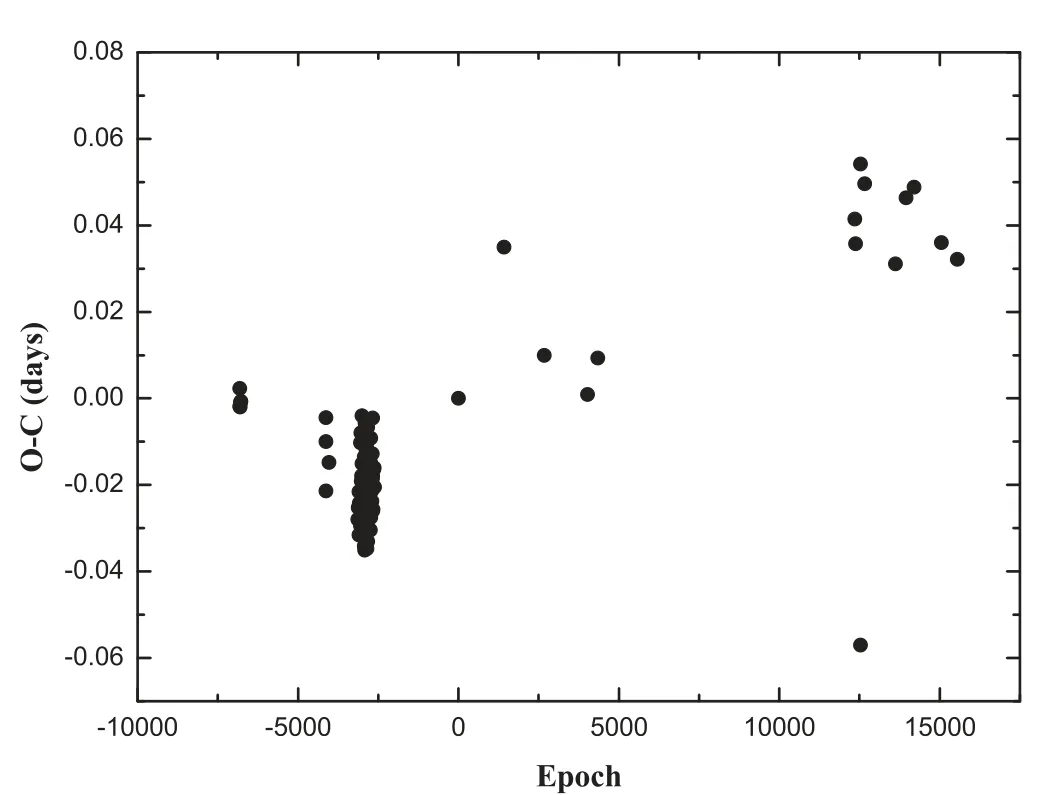
Figure 4.O?C diagram of NW Leo computed with the old linear ephemeris.

3.Orbital Period Changes and Photometric Solutions of NW Leo

3.1.Orbital Period Correction

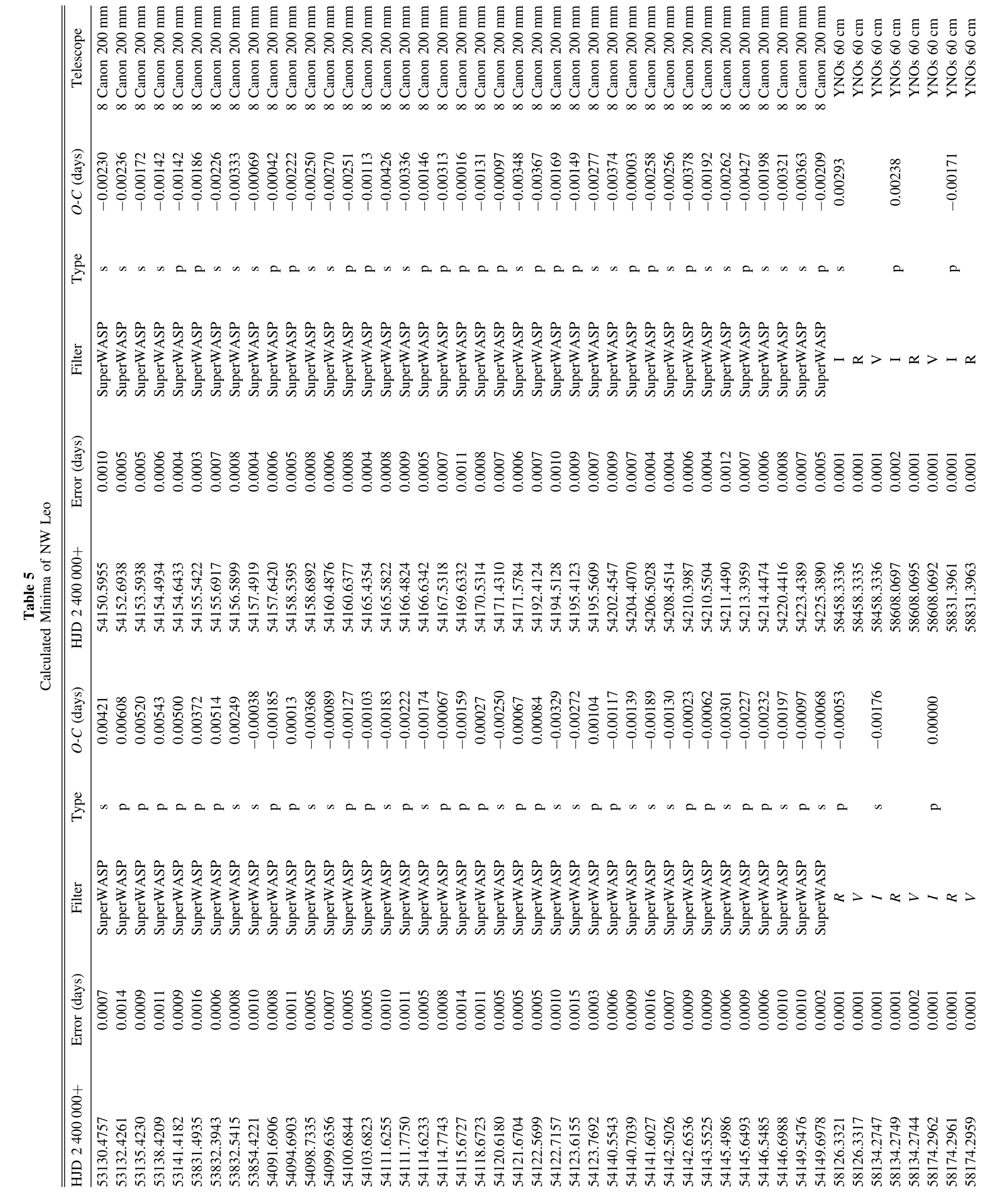
From 2018 to 2020,we observed NW Leo many times by using the 60 cm telescope administered by Yunnan Observatories.Several minima were obtained(see Table 5).The CCD is Andor DW436 and the filter system is Johnson–Cousin–Bessel.Coordinates of the comparison star and check star are listed in Table 1.VRIthree band LCs were obtained and the phases were computed with the linear ephemeris given by Diethelm(2010),

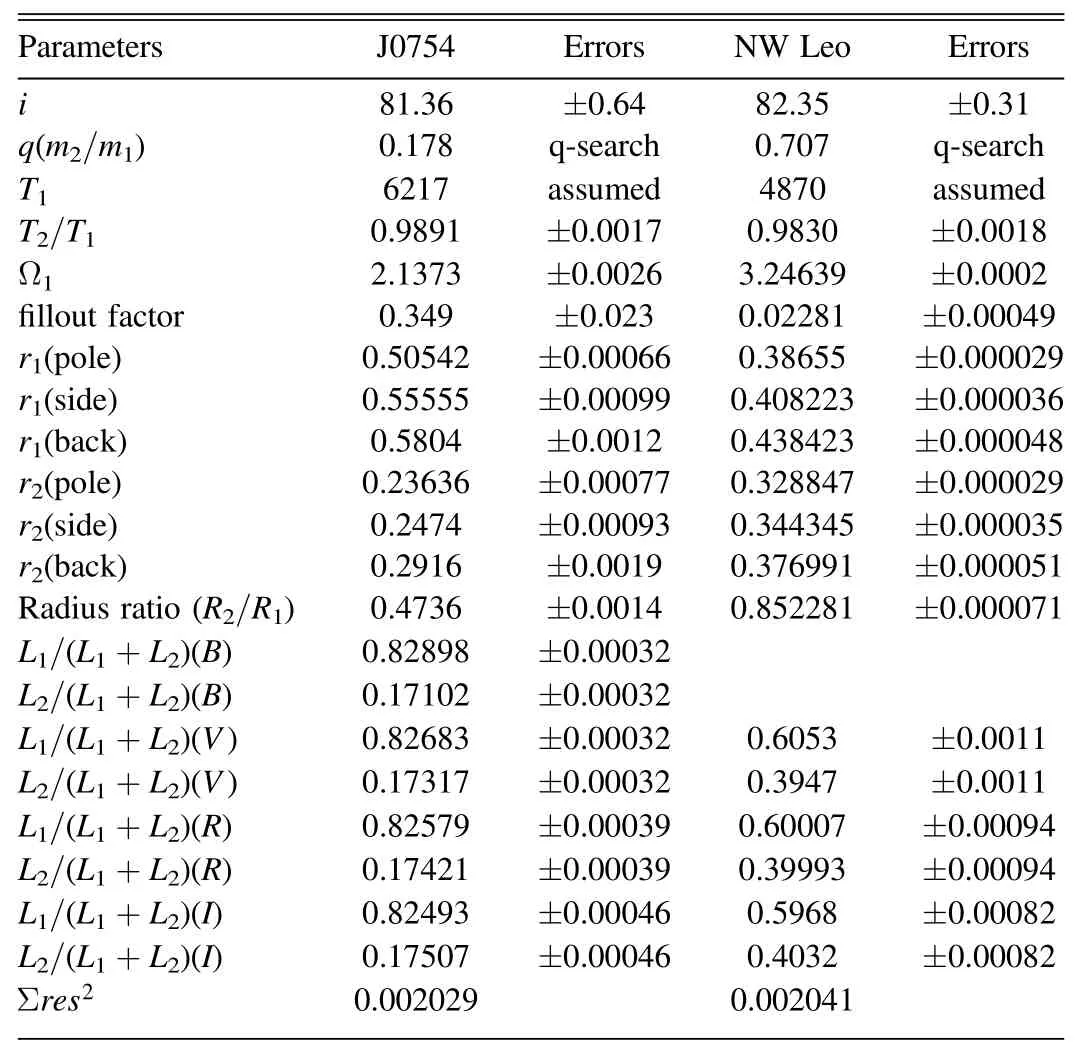
Table 2Photometric Solutions

However,the result suggests that the orbital period needs to be revised(see Figure 3).To correct the orbital period,all available minima from literature were collected(see Table 4),in addition,partial LCs of NW Leo were found from SuperWASP sky survey data(Butters et al.2010)and a group of minima were obtained(see Table 5).TheO?Cdiagram is displayed in Figure 4.TheO?Ctrend also indicates that the current orbital period of NW Leo is incorrect.If the orbital period in an ephemeris is wrong,due to the cumulative effect,one cannot calculate the values ofEandO?Ccorrectly.In this case,it is impossible to get a correctO?Ctrend and hence the correct period changes.This situation is similar to VW Boo(Qian&Zhu 2002)and Qian et al.(2005).

Figure 5.O?C diagram of NW Leo computed with the newly derived linear ephemeris.The red line represents the fitting curve,which suggests a cyclic period variation.

Based on all the minima,a revised linear ephemeris was derived,

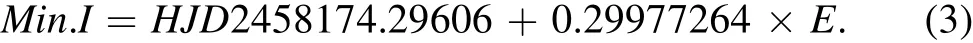
TheO?Cvalues of all minima from the revised linear ephemeris were calculated (see Tables 4 and 5).The correspondingO?Cdiagram is plotted in Figure 5,and a leastsquares solution leads to the following nonlinear ephemeris,

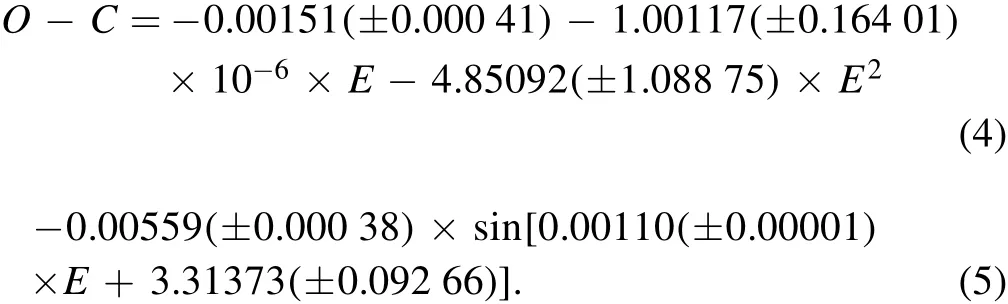
The fitting curve and the residuals ofO?Cfrom Equation(4)are displayed in Figure 5.

3.2.Photometric Solutions of NW Leo

Using the revised linear ephemeris(Equation(3)),we recalculated the phases ofVRILCs(see Figure 6).Then,the LCs were analyzed with the W-D code.The spectral type(K3)and the effective temperature of primary component(4870 K)were given by LAMOST.The gravity-darkening coef ficients were set asg1=g2=0.32 and bolometric albedo asA1=A2=0.5.

During the modeling,Mode 3 was utilized,and the adjustable parameters were orbital inclination(i),effective temperature of star 2(T2),monochromatic relative luminosity of star 1(L1V,L1R,L1I)and dimensionless potential of star 1(Ω1).Due to the LCs showing asymmetry(the O’Connell effect),we add a spot on the primary component.Since there is no spectroscopic mass ratio,the mass ratio(q)is determined by the q-search method.The photometric solutions are listed in Table 2,which indicate that NW Leo is an A-subtype contact binary with a high mass ratio.Theoretical LCs and the con figuration of NWLeo are plotted in Figures 7 and 8,respectively.

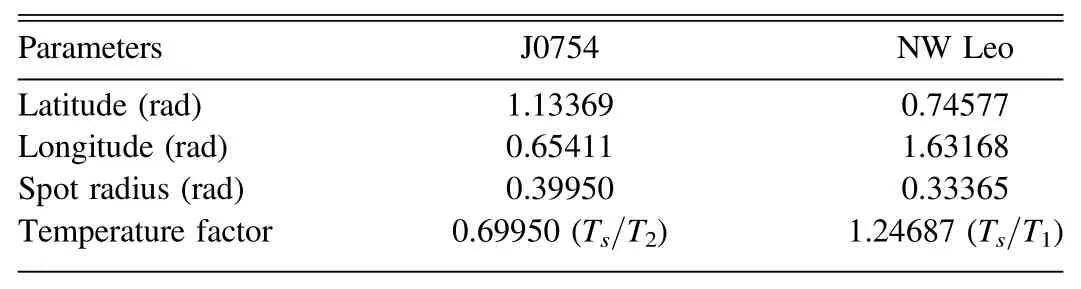
Table 3Parameters of Spots

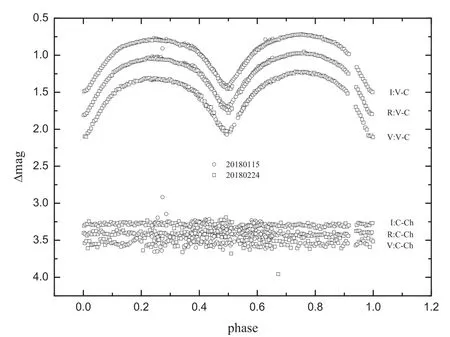
Figure 6.Top:Observed VRI LCs of NW Leo.Bottom:The magnitude difference between the comparison star and check star.

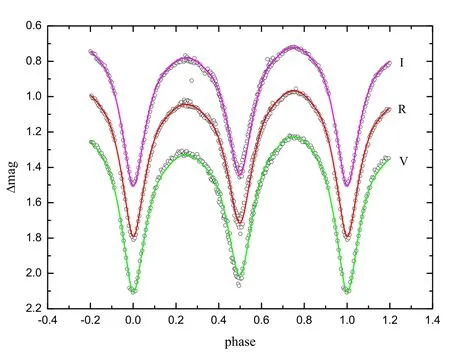
Figure 7.Observed VRI LCs of NW Leo and its theoretical LCs with a hot spot on the primary component.

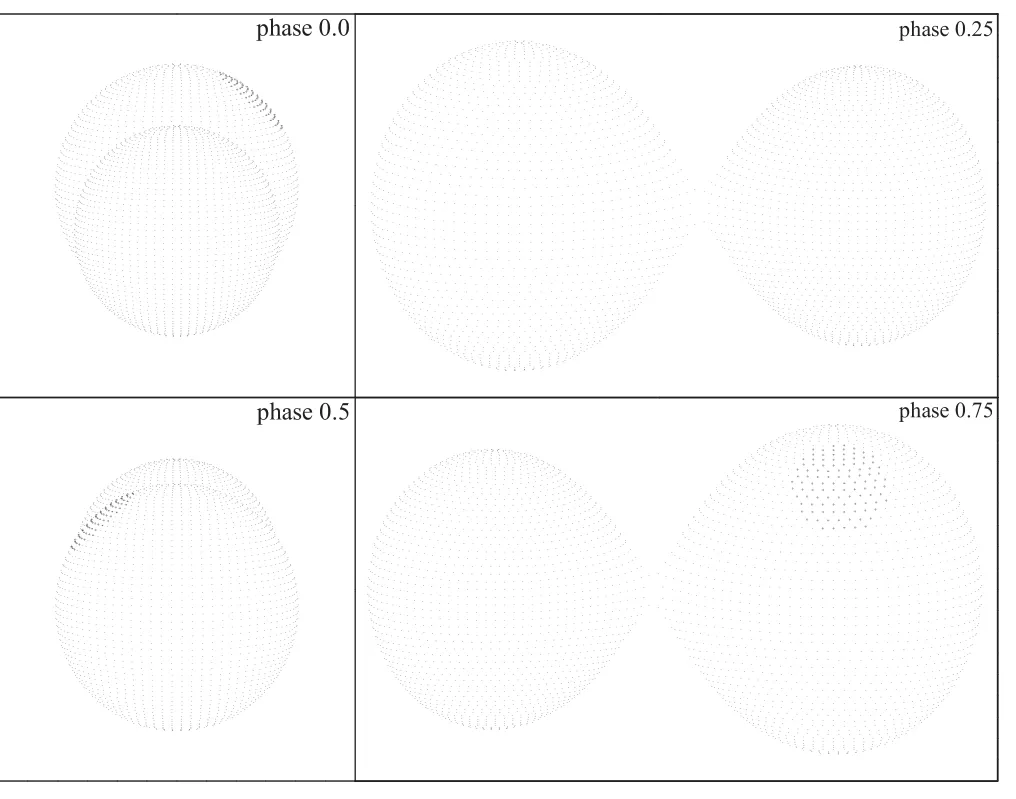
Figure 8.Con figuration of NW Leo and location of the spot.

4.Discussions

4.1.A Possible Explanation for the Asymmetry of Light Curves in CSS J075415.6+191052

Comparing the observed LCs with the theoretical ones,we found thatBVband LCs are totally symmetric butRIbands are not(see Figure 2).Usually,we use magnetic activity to explain the asymmetry of LCs in late type contact binaries.Due to both components of contact binaries filling their Roche lobes,an impact spot caused by mass transfer is also possible.However,for CSS J075415.6+191052,just theRILCs are a little weak(not enhanced)around the left shoulder of the secondary minimum,so we first exclude the first case because there is no reason that the magnetic activity spot only affectsRIband light.Now that the LCs become weak,it should be a dark spot(not a hot spot),according to the Wien displacement law,with the temperature decreasing,and long wavelength radiation becoming stronger.Some good examples of this effect can be found in previous studies[e.g.,V473 Cas(Zhu et al.2009);SuperWASP J015100.23-100524.2 (Qian et al.2015);1SWASP J030749.87-365201.7(Liu et al.2018a)].However,now the fact is that short wavelength LCs are unchanged while long wave ones are weakened,which means that a dark spot associated with magnetic activity cannot be the explanation for the asymmetry of LCs in this case.

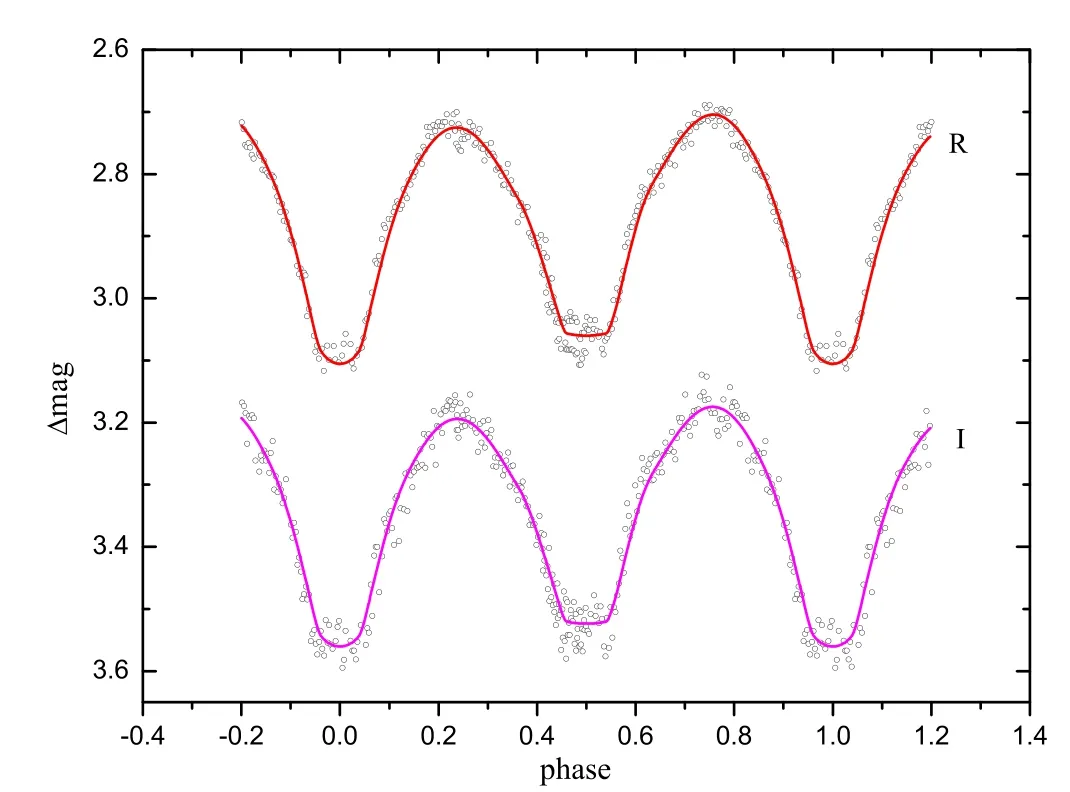
Figure 9.Observed RI LCs of CSS J075415.6+191052 and its theoretical LCs with a cool spot on the secondary component.

What if the asymmetry in LCs is the result of mass transfer?There are two scenarios:First,mass transfers from the primary component to the secondary.Because this target is an A-subtype contact binary,the primary component is the hotter one.In this case,the result should enhance the LCs,which contradicts the fact that the LCs become weak,so this is impossible.Second,mass transfers from the secondary component to the primary.As mentioned in Section 2,the spot should appear around phase 0.75–1.However,the weakening of LCs occurs at phase 0.25–0.5.Therefore,this is also unreasonable.In conclusion,the asymmetry of LCs in CSS J075415.6+191052 is not the result of mass transfer between the two components.

Liu et al.(2018b)proposed that the mass transfer between the two components should first go through a common convective envelope,and the common envelope will keep this part of the mass temporarily.With the accumulation of mass,it will eventually be released.In this case,when the mass stays in the common envelope,it probably absorbs certain wavelengths of light,which results in the weakening of certain LCs.As we discussed above,if mass transfers from the secondary component to the common envelope,the phase of the weakened LCs is not expected.So,the only possibility is that mass transfers from the primary component to the common envelope through the inner Lagrangian point.If so,when the transferring mass is moving out from the primary component,according to conservation of angular momentum,it will first appear at phase 0.25 and close to the neck of the binary system.Therefore,we added a dark spot on the secondary component near the inner Lagrangian point.Just as we expected,photometric solutions converged soon.TheoreticalRILCs with a dark spot on the secondary component can be seen in Figure 9.Obviously,this fitting result is better than before.The location of the spot is listed in Table 3 and its structure is depicted in Figure 10.

Figure 10.Con figuration of CSS J075415.6+191052 and the location of the spot.

Table 4Minima of NW Leo from Literature

4.2.Possible Explanations for the Orbital Period Changes of NW Leo

The quadratic term in Equation(4)reveals a long-term period decrease,which may be caused by the mass transfer from the primary to the secondary component.However,the long-term decreasing trend is not obvious,and more observations are needed to check this trend.The sine term suggests a periodic change with an amplitude of 0.005 59 days,and the modulation period is about 4.7 yr.The cyclic period variations of close binaries were often explained by magnetic activity ofcomponents(Applegate 1992)or light travel time effect of a third body(Liao&Qian 2010).

For the first case,the energy required to cause the cyclic period change can be estimated by a method described by Brinkworth et al.(2006),and the result is displayed in Figure 11.Since there is no radial velocity study of NW Leo,the masses of both components cannot be determined accurately.For contact binaries,we can estimate the parameters using empirical equations given by Gazeas(2009).Compared with the energy required to produce the cyclic period change,the total energy radiated by the primary component during the whole modulation period did not meet the requirement.Therefore,the Applegate mechanism cannot explain the cyclic oscillation.

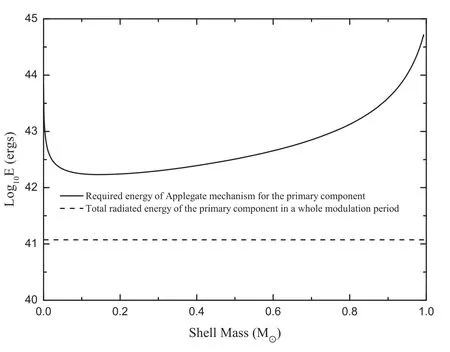
Figure 11.Energy required to cause the Applegate mechanism.

In this situation,the most plausible explanation of the cyclic period change in NW Leo is the light travel time effect of a third body.The mass function of the tertiary companion can be computed utilizing the following equation

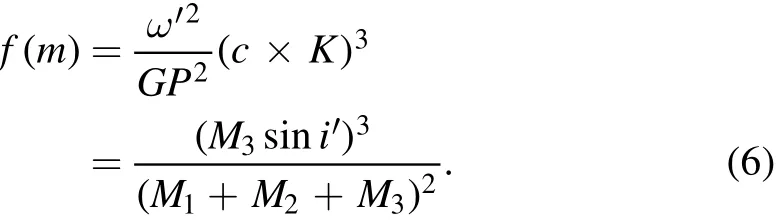
w′is the periodic angular frequency,Pis the orbital period of the binary,Kis the amplitude of the cyclic variation,cis the speed of light andi′is the orbital inclination of the third body.Because the periodic oscillation term is a standard sine function,it corresponds to the situation in which the third body is moving in a circle at a constant speed,soi′cannot be too small,which means sini≈1.In order to get accurate information about the additional companion,a radial velocity study is needed.

4.3.P–J′orb Diagram

S.B.Qian et al.(2021,in preparation)computed the speci fic angular momentaof binary systems for all the samples compiled by Zhang&Qian(2020b),and the relation between orbital period andis shown in Figure 12.With the evolution of contact binaries,the angular momentum remains constant or decreases but cannot increase.Therefore,the evolution direction of the contact binaries should be top-down in Figure 12.Samples near the upper boundary have greater speci fic angular momentum,which suggests that they are at the beginning of the contact phase.At this stage,contact binaries mainly follow the TRO theory.In contrast,samples near the lower boundary have lost much angular momentum,and they abide by the AML theory.This indicates that TRO and AML may play important roles in the evolution of contact binaries,and with AML gradually taking the dominant position,contact binaries will tend to merge.

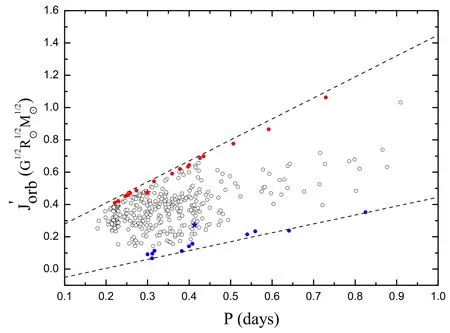
Figure 12.The relation between orbital period and speci fic angular momentum.The positions of CSS J075415.6+191052 and NW Leo in the diagram are marked with a blue star and red star,respectively.

For comparison,the positions of CSS J075415.6+191052 and NW Leo in Figure 12 are marked with a blue star and red star,respectively.One can clearly see that CSS J075415.6+191052 is near the lower boundary while NW Leo is close to the upper boundary.That is to say,CSS J075415.6+191052 is more evolved than NW Leo,which is in agreement with their photometric solutions.CSS J075415.6+191052 is now dominated by AML,and it has a low mass ratio and slightly deep degree of contact.However,NWLeo mainly follows TRO in the current stage,and it has a high mass ratio and shallow degree of contact.

5.Conclusions

LC asymmetry is very common in close binaries,especially in W UMa-type contact binaries.Because both components of a contact binary fill their Roche lobes and share a common convective envelope,mass and energy transfer are possible.Due to the frequent interactions between the two components,the evolution of contact binaries becomes very complicated.The new photometric analysis suggests that CSS J075415.6+191052 is a low mass ratio A-subtype contact binary with contact degree of 34.9%.Compared with the theoretical LCs,the observedRIband LCs seem to be a little weaker around the left shoulder of the secondary minimum,whereasBVwave band LCs are not.After detailed discussion,a dark spot that arises from mass transferring from the primary component to the common convective envelope results in this effect.This mechanism,dominated by the common convective envelope,is con firmed,which once again highlights its special role in the evolution of contact binaries.

Based on the photometric study of NW Leo,we conclude that it is a high mass ratio,shallow contact binary(f=2.3%).Furthermore,itsO?Ccurve features periodic changes and the modulation period is only about 4.7 yr.The total energy radiated from the primary component in the whole modulation period is less than the energy required to produce the cyclic period change,therefore,the cyclic oscillation is caused by the light travel time effect of a third body.TheO?Ctrend also indicates that there is a long-term decrease in its orbital period,which may be caused by mass transfer from the primary to the secondary component.However,the number of current minima is still limited,and the long-term decreasing trend is not obvious.Therefore,more observations are needed to check this trend.

Further study shows that NW Leo is dominated by TRO theory,while CSS J075415.6+191052 mainly follows AML theory.The relation between orbital period and speci fic angular momentum suggests that the evolution of contact binaries is TRO+AML.For low mass ratio contact binaries,AML will lead to the merger of the binary systems.

?

?

Acknowledgments

This study is supported by the National Natural Science Foundation of China(Grant Nos.11933008 and 11903076),the Science Foundation of Yunnan Province(202001AT070051),the Foundation of Science and Technology of Guizhou Province(Nos.(2016)4008,(2017)5726-37)and the Foundation of Guizhou Provincial Education Department(No.KY(2020)003).