K.Y.Roobiat and R.Pazhouhesh

Department of Physics,Faculty of Sciences,University of Birjand,Birjand,Iran;rpazhouhesh@birjand.ac.ir

Received 2021 October 13;revised 2021 November 21;accepted 2021 November 24;published 2022 February 2

Abstract Two eclipsing binary systems,UZ Lyr and BR Cyg,are semi-detached types whose secondary component fills its Roche lobe.Although radial velocity and light curves of these systems have already been investigated separately,both their radial velocity and light curves are analyzed simultaneously for the first time in the present study.Also,the orbital period changes of these systems are studied.Our results show that the mass transfers between components have negligible effects on the orbital period changes of these systems,but two light travel time effects are the reasons for the periodic behavior of the O?C curve for UZ Lyr.We could not remark more information about orbital period changes for BR Cyg,but we find a new orbital period for it.By radial velocity and light curve analysis,we find a cold spot on the secondary component of BR Cyg.The new geometrical and physical parameters of both systems are obtained and their positions on the H-R diagram are demonstrated.

Key words:(stars:)binaries(including multiple):close–(stars:)binaries:eclipsing–stars:individual(UZ Lyr,BR Cyg)

1.Introduction

UZ Lyr has been considered for a long time as an Algol-type eclipsing binary system(Nijland 1931).However,this system has not been targeted for photometry,and a detailed light curve analysis has not been available.In this regard,Koch et al.(1979)classi fied this system as“forgotten”.This system was included in the catalog of variable stars in the Kepler project in 2009(Pigulski et al.2009),and then it was included in the first Kepler eclipsing binary catalog.The speci fied temperature ratio ofand an effective temperature ofTeff=11,061Kwas reported in this catalog(Prsa et al.2011).This temperature ratio was changed to 0.51276 in the second Kepler eclipsing binary catalog(Slawson et al.2011).By combining data from the Kepler project with those from HESS,KIS,and 2MASS projects,the temperature of the primary and secondary components of the system has been reported as 15,058±515 K and 10,411±2484 K,respectively by Armstrong et al.(2013).

The radial velocity curve of UZ Lyr has been obtained by Matson et al.(2017),and the value of±0.01was reported as the spectroscopic mass ratio.The absolute masses of the primary and secondary components were calculated as 4.05±0.3M⊙a(bǔ)nd 0.92±0.07M⊙,respectively.Moreover,they usedT1=11,061 K for the primary component temperature which is known asTeffof the system in the Kepler eclipsing binary catalog (Slawson et al.2011)and the temperature of the secondary component was derived asT2=5671 K by using the ratioreported in this catalog.Furthermore,they concluded that these temperatures for UZ Lyr were probably approximated to be less than the real value due to the position of this system on the Hertzsprung-Russell(H-R)diagram(Matson et al.2017).In the LAMOST-Kepler project,the effective temperature was reported asTeff=11461±397 K with a spectral class A0IV(Frasca et al.2016).

Periodic changes of the orbital period of UZ Lyr were investigated by Rafert(1982)for the first time and a sinusoidal ephemeris was proposed for it.Hoffman et al.(2006)studied theO?Ccurve of the eclipse minima times of this system,but they were unable to con firm the assumption of the existence of a third body due to high scatter in the data.However,after publication of the Kepler project data,a large number of eclipse minima times were available for this system.Gies et al.(2012)calculated the value× 10-6yr-1based on these new data.Although they could not declare decisively about existence of a third body,Gies et al.(2015)re-examined theO?Ccurve of UZ Lyr by considering new data and found that periodic changes are most likely due to a third body or the movement of star spots.Borkovits et al.(2016)published theO?Ccurve and suggested the third body of UZ Lyr has a period of about 15 yr and a minimum mass of 0.18M⊙.

The second system,BR Cyg,was introduced as an eclipsing binary in 1924 for the first time(Wehinger 1968).In a study conducted by Kukarkin et al.(1958),the spectral type of the primary component was found to be B9.The first photoelectric light curves of BR Cyg were obtained in twoBandVJohnson filters and then were analyzed by Wehinger(1968).Kukarkin et al.(1971)re-studied the BR Cyg system and suggested spectral types of A5V and F0V for the primary and secondary components of this system respectively.Giuricin&Mardirossian(1981)analyzed the Wehinger and Harmanec photometric data and concluded that this spectral classi fication was probably incorrect.Also,they demonstrated that BR Cyg is a semi-detached system and fills the secondary component of its Roche lobe.Terrell&Gross(2005)performed CCD photometry on this system in four filters,B,V,RcandIc,and analyzed its light curves.They selectedT1=8900 K based on theB?Vcolor index and obtainedq=0.532 for the mass ratio.Liakos&Niarchos(2009)investigated the possibility of pulsation,but they could not find any evidence of pulsation.In 2009,BR Cyg was included in the catalog of variable stars of the Kepler project(Pigulski et al.2009),and also in the Kepler eclipsing binary catalog in 2011(Prsa et al.2011).In the latest edition of this catalog,the effective temperature and temperature ratio of this system have been published asTeff=8608 K andrespectively(Kirk et al.2016).However,Armstrong et al.(2013)reported the temperatures of 11,056±603 K and 6278±1228 K for the primary and secondary components,respectively and also the effective temperature was obtained as 10,849 K based on spectroscopy performed in the LAMOST-Kepler project(Frasca et al.2016).Matson et al.(2017)arrived atq=0.516 by applying the radial velocity curve of BR Cyg and calculatedM1=3M⊙a(bǔ)ndM2=1.55M⊙for the mass of the primary and secondary components respectively.Harmanec et al.(1973)analyzed the orbital period changes for the first time,but no regular behavior was observed in theO?Ccurve due to high scatter in the data.After publication of the Kepler project data and obtaining a large number of minima data for this system,Gies et al.(2012)examined the orbital period changes and reported the value ofThey attributed the reason for these changes to be either the movement of star spots or systematic changes in seasons.Moreover,they did not observe any sign of the existence of a third body for BR Cyg.These results were also con firmed by Gies et al.(2015)and Zasche et al.(2015).Zhang et al.(2019)combined the Kepler eclipsing binary catalog with the LAMOST data(for 1320 binaries)and found some parameters of this systems(e.g.,period,Teff,logg,M1,R1,...)but they did not analyze light curves of these systems.They assumed that the provided LAMOST spectra for each system depended on the brighter component.Therefore,the atmospheric parameters measured from these spectra were obtained by using a single star model.

2.Period Study

The minima times of both UZ Lyr and BR Cyg are collected from theO?Cgateway,1http://var.astro.cz/ocgate/AAVSO2www.aavso.orgdatabase and also all minima times are extracted from the Kepler eclipsing binary stars database.3http://keplerebs.villanova.eduIn total,968 primary eclipse minima times including 292 visual(vis),13 photographic(pg)and 663 CCD or photoelectric(PE)minima times have been compiled for UZ Lyr.Furthermore,1345 Min I,including 268 vis,9 pg and 1068 CCD or PE have been obtained for BR Cyg.These minima times have various validities,because they were determined with different types of observations and by using different instruments.Also,some authors may have used different numerical methods for extracting minima times from observational data.Therefore,we choose weights 1,3 and 10 for the whole group of observations obtained by vis,pg and PE or CCD techniques,respectively.This weighting method has been implemented by many authors(e.g.,Zasche et al.2008;Hanna&Amin 2013;Ulas et al.2020).

UZ Lyr system:The epoch andO?Cvalue of this system are determined by utilizing the linear ephemeris as follows(Kirk et al.2016)

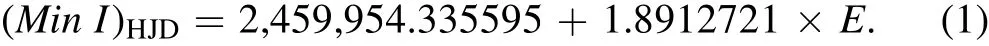
TheO?Ccurve is displayed in Figure 1.

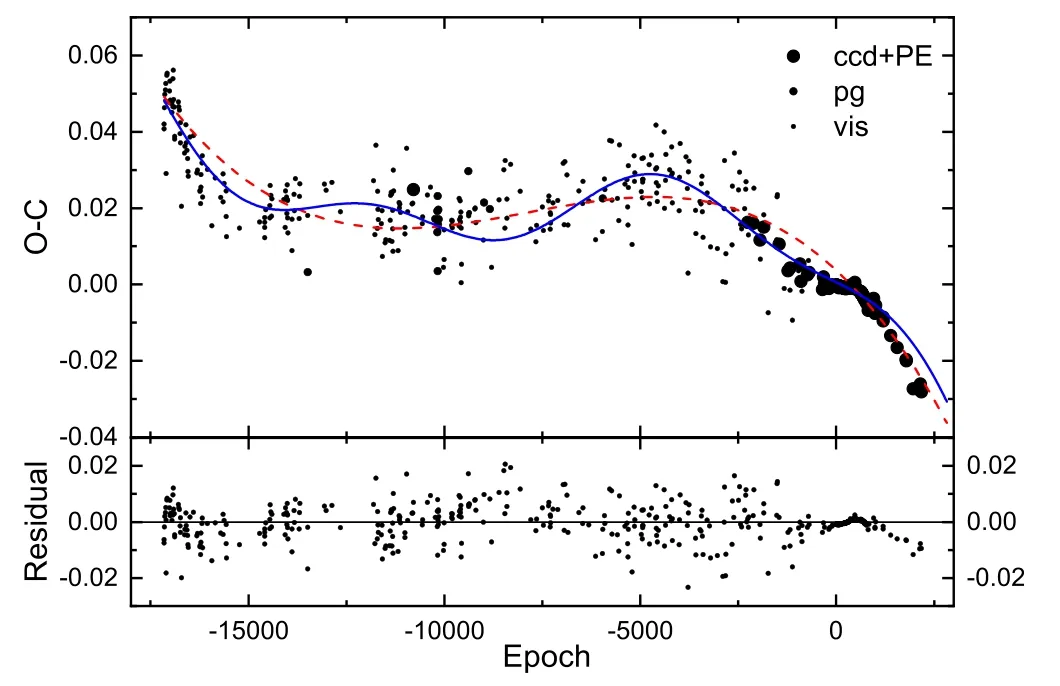
Figure 1.The O?C curve of the UZ Lyr system.The dashed line shows a fourth body and linear fit,and the solid line indicates the LTEs of both a third and fourth body and a linear function.The final residuals after removing the linear function and third and fourth body LTEs are displayed in the bottom.

We applied linear,parabolic and cubic functions in addition to one or two light travel time effects(LTE)for theO?Ccurve of this system.We concluded that a linear function with two LTEs is the best choice for this diagram,after comparing the final fitting residuals.The coef ficients of the linear function determined by employing the least squares method are as follows By using the slope of this linear function,the corrected orbital period of the binary system can be found as

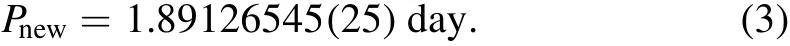
After removing the linear function from theO?Ccurve,periodic behavior is apparent in the residuals in which these changes may be due to the LTE and existence of one or more components in the system.To analyze the LTE in theO?Ccurve,the following equation has been utilized(Irwin 1959)

whereK,e,ωandνare the amplitude of changes,eccentricity,the longitude of periastron and the true anomaly of the third or fourth body,respectively.We use the Period04 program(Lenz&Breger 2005)to determine the initial values for orbital period of the third and fourth bodies.Orbital and physical parameters obtained by fitting Equation(4)to theO?Cresiduals are shown in Table 1.Figure 1 illustrates the final simulated curve and residuals.After removing the LTEs of the third and fourth bodies and the linear function,it is obvious that the final residuals are randomly scattered around the zero line with no systematic behavior.

Table 1Orbital and Physical Parameters of the Third and Fourth Bodies in UZ Lyr

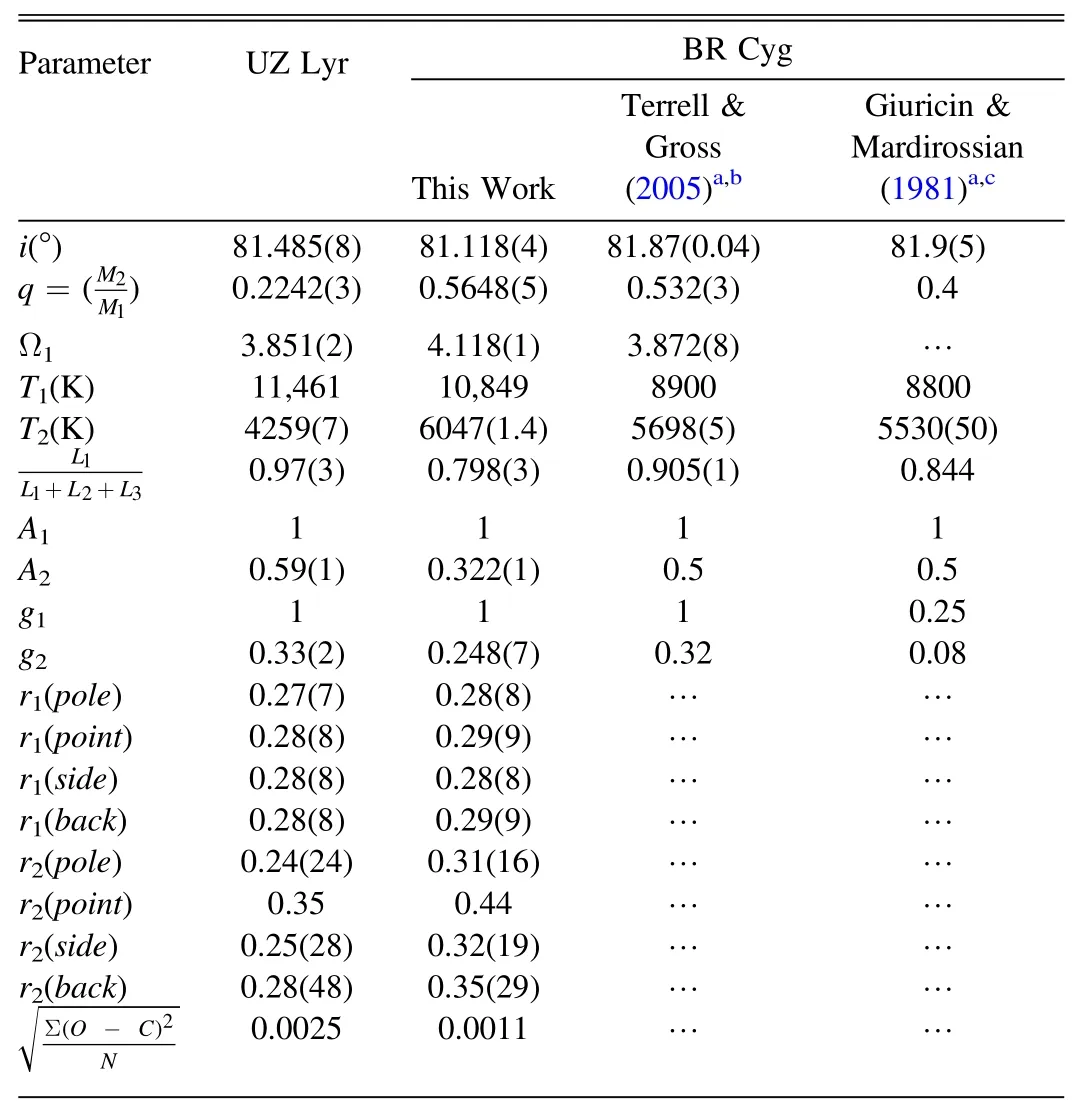
Table 2 Results from Simultaneous Analysis of the Radial Velocity and Light Curves of Both the UZ Lyr and BR Cyg Systems

BR Cyg:The epoch andO?Cvalue of this system are determined by using the linear ephemeris(Kirk et al.2016)

The obtainedO?Ccurve is depicted in Figure 2.

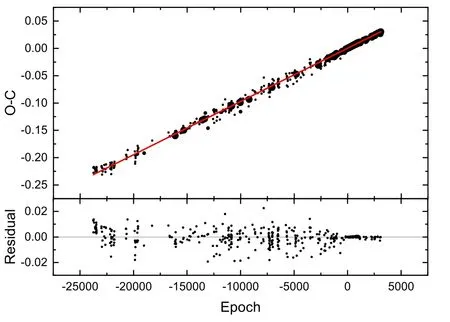
Figure 2.The O?C curve of BR Cyg.The solid line indicates the fit of a linear function to the data points.The final residuals are displayed in the lower part of the figure.

At first sight,theO?Ccurve resembles a linear function and its coef ficients are determined by applying the least squares method as follows

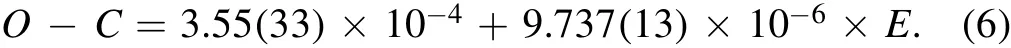
The linear changes of theO?Ccurve mean that the orbital period of the system has not been reported correctly in the initial ephemeris Equation(5).With regard to the slope of the fitted line on theO?Ccurve,it is possible to obtain the following value as the new orbital period of this system

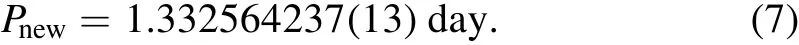
After removing the linear function from theO?Ccurve,the final residuals are randomly scattered around the zero line with no systematic or periodic behaviors.Therefore,there is no evidence of the existence of a third body or mass transfer in this system.Owing to the high scatter inO?Cdata,effects with short periodicity and low amplitude are not observable in this diagram.

3.Light Curve Analysis

The light curve data of both UZ Lyr and BR Cyg are extracted from the Kepler eclipsing binary stars database.We have used only Short Cadence(SC)data for plotting the light curves due to the high accuracy.Also,radial velocity data for these binary systems are adopted from Matson et al.(2017)and we have utilized the PHOEBE Legacy4http://phoebe-project.orgProgram(Prsa&Zwitter 2005).The light curve analysis was performed in“detached”mode first,but we could not find a good agreement between the theoretical and observational light curves,so the“semi-detached”mode was chosen,with the secondary component filling it Roche lobe for both systems.

UZ Lyr:Orbital phases were calculated by using the following linear ephemeris

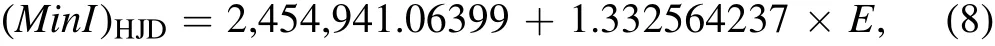
where the eclipse minima times were referenced from Kirk et al.(2016)and the period was obtained in this study.We useT1=11,461 K(Frasca et al.2016)for the temperature of the primary component as a constant parameter in the program.The initial mass ratio chosen isq=0.23,which is based on the radial velocity data provided by Matson et al.(2017),then this parameter was de fined as a free parameter in the program.BecauseT1＞7200 K,the values ofA1=1(Milne 1926)andg1=1(Zeipel 1924)are used as constant parameters for the bolometric albedo and gravity darkening coef ficients,respectively.These two parameters are considered as free parameters for the secondary component.We apply the logarithmic law for limb darkening coef ficients,which was automatically calculated by the program(Castelli&Kurucz 2003).Finally,radial velocity and light curve data are analyzed simultaneously,and the results are given in Table 2.Figures 3 and 4 feature the theoretical and observational light and radial velocity curves of UZ Lyr,respectively.

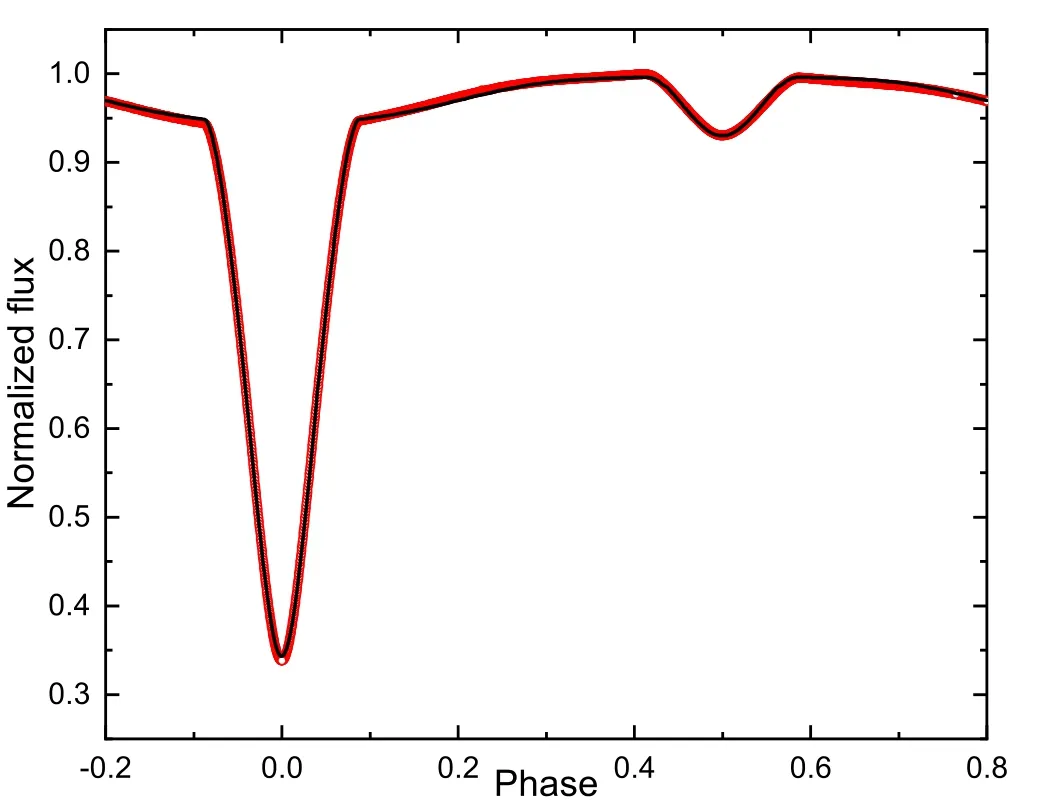
Figure 3.Theoretical(solid black line)and observational(red dots)light curves of the UZ Lyr system.

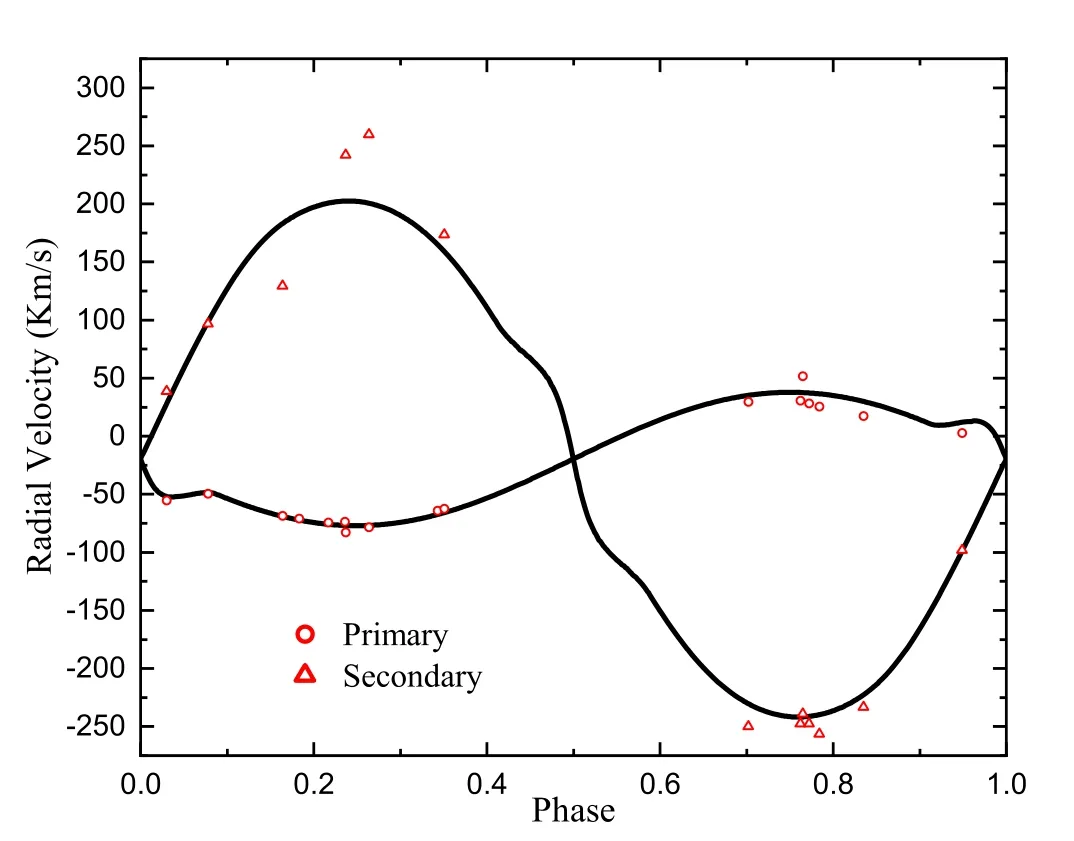
Figure 4.Theoretical and observational radial velocity curves of the UZ Lyr system.

In Figure 5,the three-dimensional geometry of system is displayed.Accordingly,the values ofK1andK2are determined as 57.4±4.5 km s?1and 222±7 km s?1,respectively,which can be used for calculation of the absolute parameters of UZ Lyr.Table 3 lists the absolute physical and geometrical parameters for this system.

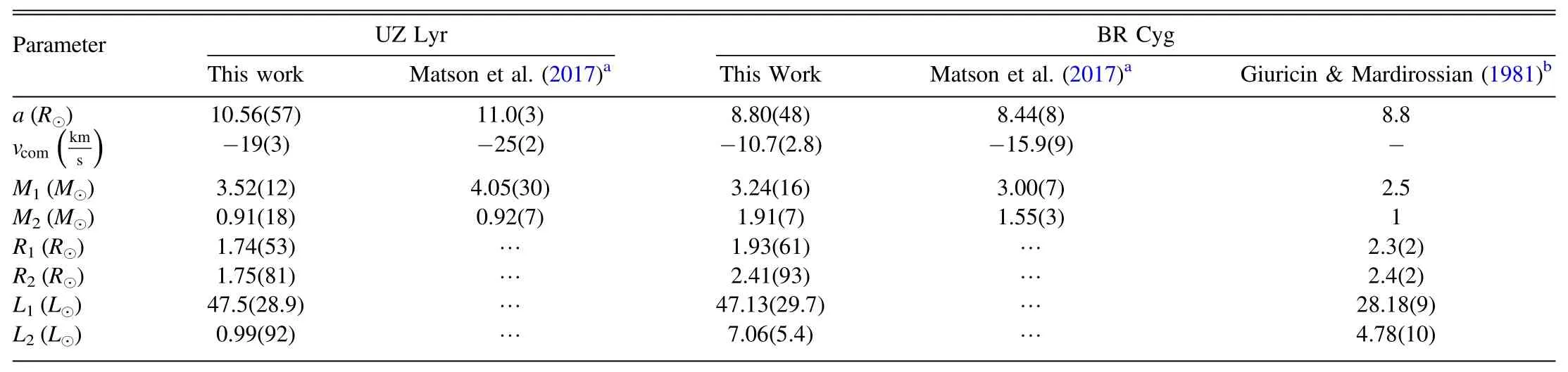
Table 3Absolute Physical and Geometrical Parameters of the UZ Lyr and BR Cyg Systems

Table 4Characteristics of a Spot on the Secondary Component of BR Cyg

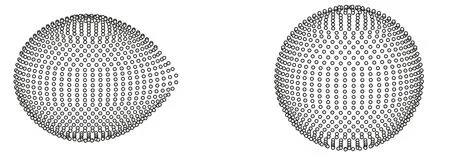
Figure 5.Three-dimensional geometry of UZ Lyr at phase 0.75.The secondary component fills its Roche lobe,while the primary component retains a nearly spherical shape.

BR Cyg:The following linear ephemeris was used

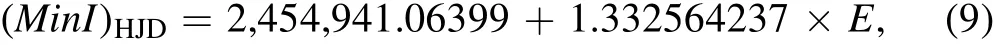
where the obtained period in this study and the eclipse minima time reported in Kirk et al.(2016)are used.T1=10,849 K was chosen based on spectroscopy performed in the LAMOSTKepler project(Frasca et al.2016).The mass ratio was considered as a free parameter with the initial value of 0.516 based on the radial velocity curve presented by Matson et al.(2017).Because the primary temperature isT1＞7200 K,the bolometric albedo,gravity and limb darkening coef ficients of the primary and secondary components were treated similarly to the above section.The asymmetry of the light curve at phases 0.25 and 0.75 can be attributed to the existence of cold or hot spots on one of the components(O’Connell 1951).So,we consider a cold spot on the secondary star and change its position,temperature ratio and radius to achieve the best fit between the theoretical and observational light curves.Table 4 gives the characteristics of this spot.Data on radial velocity and light curves are analyzed simultaneously,and the results are provided in Table 2.Figures 6 and 7 feature the theoretical and observational light and radial velocity curves of BR Cyg,respectively.Figure 8 depicts the three-dimensional geometry of this system with the position of a cold spot on the secondary component.

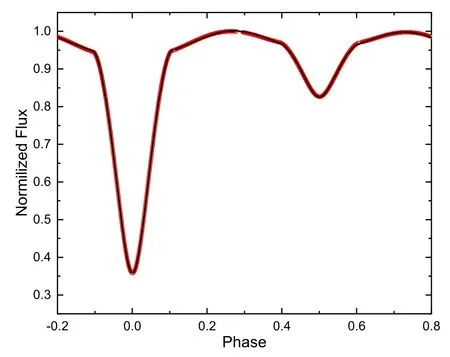
Figure 6.Theoretical(solid black line)and observational(red dots)light curves of BR Cyg.

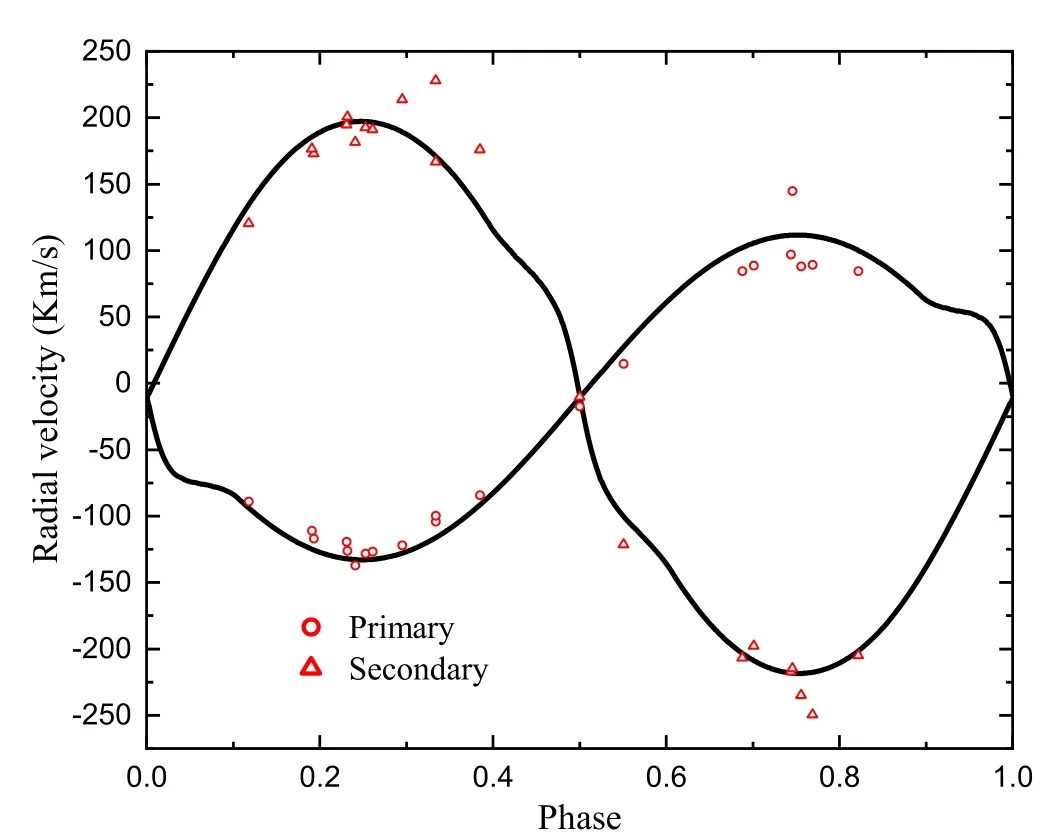
Figure 7.Theoretical and observational radial velocity curves of BR Cyg.

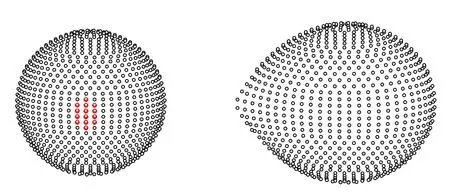
Figure 8.Three-dimensional con figuration of BR Cyg at phase 0.25.The secondary component fills its Roche lobe,and the primary component retains a nearly spherical shape.The position of a cold spot on the secondary star is also displayed.

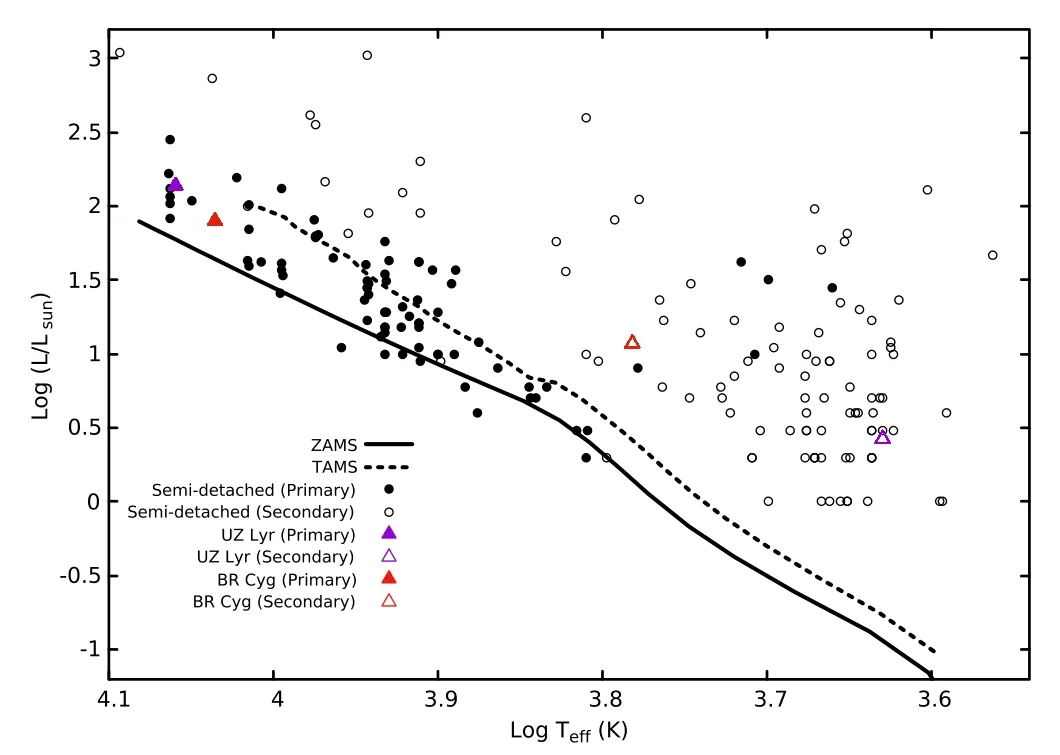
Figure 9.The positions of the primary and secondary components of UZ Lyr and BR Cyg in the H-R diagram.The examples of semi-detached binary systems were referenced from Malkov(2020).The zero age main sequence(ZAMS)and terminal age main sequence(TAMS)lines for metalisity like the Sun were obtained from MESA-Web.(http://mesa-web.asu.edu).

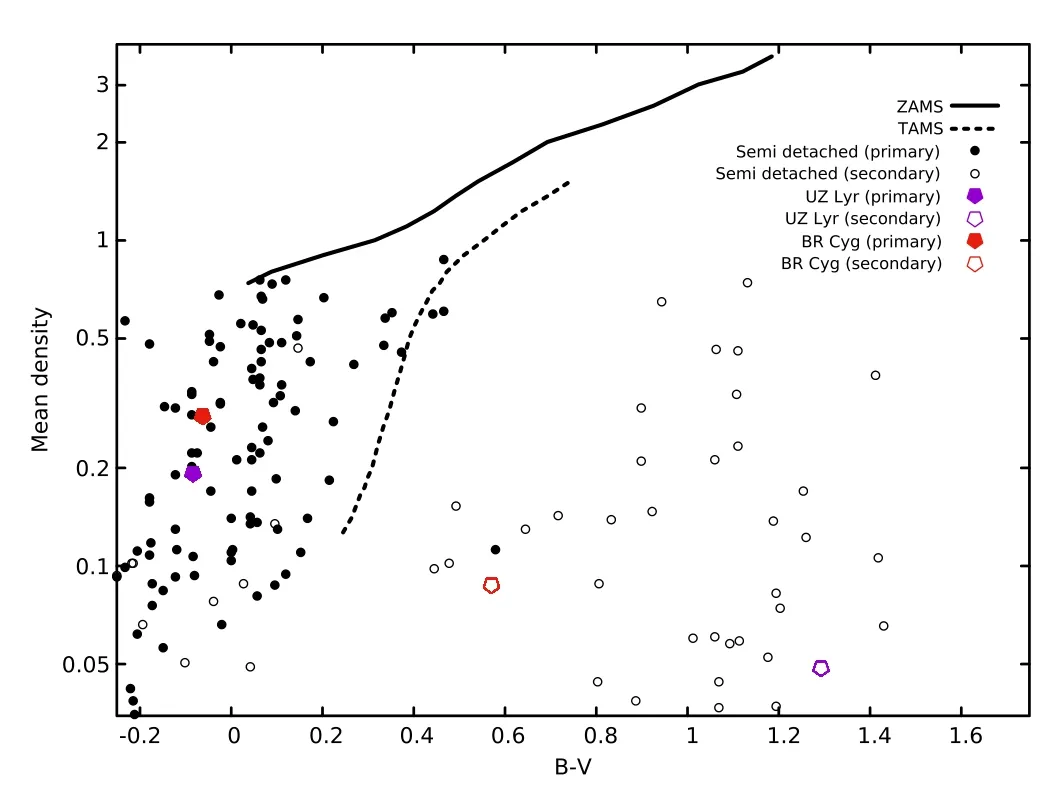
Figure 10.Color index vs.density diagram with the positions of the primary and secondary components of the UZ Lyr and BR Cyg systems.Examples of semi-detached binary systems were taken from Malkov(2020).The ZAMS and TAMS lines were adopted from Worthey&Lee(2011).

Accordingly,the values ofK1andK2are determined as 122.26±3.1 km s?1and 207.86±4.2 km s?1,respectively.The absolute physical parameters of BR Cyg are calculated and given in Table 3.

The H-R diagram is a useful tool for exploring a star’s evolutionary status.Figure 9 displays the position of the primary and secondary components of these systems in the H-R diagram based on the absolute parameters obtained for both the UZ Lyr and BR Cyg systems.For comparison,some other semi-detached binaries(Malkov 2020)are also shown in this figure.Accordingly,it is clear that in both systems,the secondary component left the main sequence toward the red giant phase,but the primary component still remains on the main sequence.The color index vs.density diagram also shows the evolutionary status of stars(Mochnacki 1981,1984,1985).Now by using the parameters in Table 3,we can calculate the average density of the primary components for the UZ Lyr and BR Cyg systems as 0.193 gr cm?3and 0.289 gr cm?3,and also the corresponding secondary components are 0.049 gr cm?3and 0.088 gr cm?3,respectively.Tables published in Worthey&Lee(2011)can be used for calculation of theB?Vcolor index for the primary and secondary components of these systems which result in?0.083 and 1.29 for UZ Lyr and?0.063 and 0.57 for BR Cyg,respectively.Finally,the speci fied positions of both systems in the color index vs.density diagram are displayed in Figure 10.

4.Discussion and Conclusion

The radial velocity and light curves of the eclipsing binary UZ Lyr were analyzed simultaneously for the first time,and the orbital and absolute parameters of this system were obtained.First,light curve analysis was performed in“detached”mode,but there was no good agreement between the theoretical and observational light curve in this mode.So,we applied the“semi-detached”mode and consequently found the secondary component filled its Roche lobe.Our study of orbital period changes indicated a linear and two periodic behaviors.So,the mass transfer does not have signi ficant effects on orbital period changes.Also,the third and fourth bodies have minimum masses of 0.31494M⊙a(bǔ)nd 0.55187M⊙respectively and are associated with LTEs which are caused by these periodic changes.Borkovits et al.(2016)assumed a cubic function and a third body with minimum mass of 0.17M⊙for this system,but we examined this possibility and we found our result(linear function and two LTEs effect)better matched the data.According to our analysis,the effect of the third body light on the light curve of UZ Lyr was less than 1%,which can be ignored due to the calculation errors.Thus,the third and fourth body lights were not observable in the light curve.Since the minimum masses achieved for these two additional components were within the mass range of white dwarfs,0.2＜MWD＜1.2M⊙(Kepler et al.2007;Kilic et al.2007),the third and fourth bodies would be either a white dwarf or a brown dwarf.This periodic behavior of theO?Ccurve also can be induced by other factors,such as magnetic activity(Applegate effect),but due to the absence of any spot on both of the components,this will be unlikely.After elimination of the effects of mass transfer and the third body of theO?Ccurve,no systematic behavior was observed in the residuals,which could be due to scatter in the data.Thus,it is impossible to make a statement about other factors which in fluence the orbital period changes.

The radial velocity and light curves of the BR Cyg binary were also analyzed simultaneously for the first time and the orbital and absolute parameters of this binary system were derived.First,the“detached”mode was used for the analysis of the light curve,but due to the absence of good results,the“semi-detached”mode was chosen.Study of the orbital period changes of BR Cyg revealed a linear behavior.Therefore,the period suggested by Zasche et al.(2015)(Equation(5))is not correct,so the new orbital period was found to be 1.332564237 day after determining the slope of the linear fit function to theO?Ccurve.After modi fication of the orbital period and redrawing theO?Ccurve,the final data points were scattered randomly around the zero line and no systematic behavior was observed.Thus,it is impossible to discuss more about orbital period changes with such available data.The positions of the primary and secondary components of both the UZ Lyr and BR Cyg systems were shown on the color index vs.density and H-R diagrams.As seen from Figures 9 and 10,the positions of components of both systems are in agreement with other well known semi-detached binary systems.So,the secondary components have left the main sequence position toward the red giant phase but the primary components are still on the main sequence position.According to Popper(1980),for semi-detached binary classi fication,both of those systems belong to the“hot semi-detached”class(because the primary component temperature is larger than 7500 K).These systems often will evolve with the scenario named“case A”and therefore the mass transfers to the less massive component or out of the system when the components are on the main sequence.At first,the more massive component will lose most of it mass in the non-conservative process of stellar winds and the secondary component will gain just a little mass.As a result,a non-evolved primary component will gain mass and usually it has smaller size and is also hotter and more massive than the secondary component,but an evolved secondary component is more luminous and will lose its mass(De Greve 1986).So,our results are in agreement with the above scenario and positions of both systems on the H-R diagram and color-index vs.density diagram are shown correctly.

ORCID iDs

R.Pazhouhesh https://orcid.org/0000-0002-9160-1666