一類(lèi)具有基爾霍夫型弱阻尼和對(duì)數(shù)非線性項(xiàng)的半線性波動(dòng)方程
楊怡, 方鐘波
( 中國(guó)海洋大學(xué)數(shù)學(xué)科學(xué)學(xué)院, 山東青島 266100)
1.引言
我們考慮一類(lèi)具有基爾霍夫型弱阻尼和對(duì)數(shù)非線性項(xiàng)的半線性波動(dòng)方程
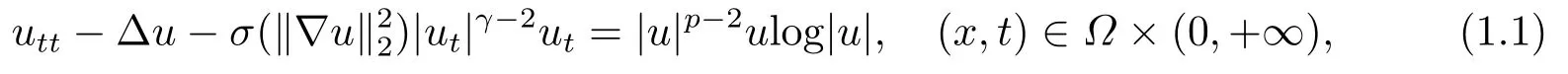
給出齊次Dirichlet邊界條件和初始條件
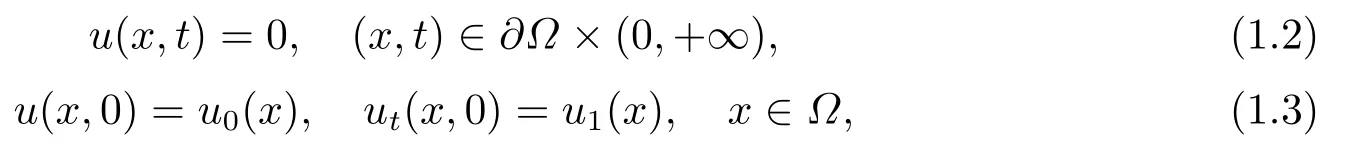
其中? ?RN(N≥1)為具有光滑邊界??的有界區(qū)域, 基爾霍夫型阻尼系數(shù)σ, 參數(shù)p和γ滿(mǎn)足

比如, Georgiev和Todorova[2]研究了方程(1.4)中g(shù)(ut) = a|ut|γ?2ut情形且在齊次Dirichlet邊界條件下, 證明了問(wèn)題解的整體存在性及有限時(shí)刻爆破現(xiàn)象.之后, 文[3]給出了具有任意負(fù)初始能量及正初始能量解的爆破現(xiàn)象.
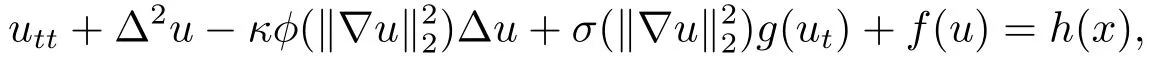
其中g(shù)(ut) ≈|ut|γut.他們?cè)贒irichlet邊界條件和鉸接邊界條件下建立了強(qiáng)解的適定性并給出了解的長(zhǎng)時(shí)間動(dòng)力行為.最近, ZHANG等[5]研究了具有退化非局部非線性阻尼項(xiàng)和乘冪型源項(xiàng)的半線性波動(dòng)方程Dirichlet初邊值問(wèn)題
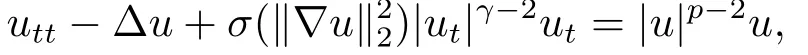
且利用位勢(shì)井理論得到了能量的衰減估計(jì)和有限時(shí)刻解的爆破現(xiàn)象.
另一方面, 關(guān)于具有常數(shù)阻尼系數(shù)和對(duì)數(shù)非線性項(xiàng)的半線性波動(dòng)方程研究也有一些新的進(jìn)展, 其主要難點(diǎn)在于對(duì)數(shù)非線性源項(xiàng)的單調(diào)性和符號(hào)無(wú)法確定.Cazenave和Haraux[6]首次考慮了具有對(duì)數(shù)非線性項(xiàng)的Schr?odinger方程及Klein-Gordon方程Cauchy問(wèn)題解的存在性與唯一性.之后, ZHANG等[7]考慮了具有弱阻尼的模型Dirichlet初邊值問(wèn)題并得到了問(wèn)題解的整體存在性及能量的指數(shù)衰減估計(jì)值.最近, 我們?cè)谖腫8]中研究了具有對(duì)數(shù)源和強(qiáng)阻尼的半線性波動(dòng)方程Dirichlet初邊值問(wèn)題

且利用位勢(shì)井理論和對(duì)數(shù)Sobolev不等式, 得到了問(wèn)題的整體可解性及能量衰減和無(wú)限爆破結(jié)果.文[9]的作者將方程(1.5)推廣到具有更一般形式對(duì)數(shù)非線性項(xiàng)情形.LIAN和XU[10]考慮了具有強(qiáng)弱阻尼和對(duì)數(shù)源項(xiàng)的非線性波動(dòng)方程Dirichlet初邊值問(wèn)題
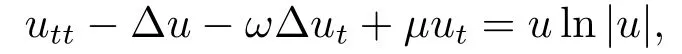
他們利用壓縮映射原理, 位勢(shì)井方法及微分不等式技巧, 證明了問(wèn)題的可解性, 能量衰減及解的無(wú)限爆破現(xiàn)象.此外, 關(guān)于具有時(shí)滯阻尼的板模型問(wèn)題的最新進(jìn)展, 我們閱讀了文[11].
綜上所述, 關(guān)于基爾霍夫型弱阻尼項(xiàng)和對(duì)數(shù)非線性項(xiàng)競(jìng)爭(zhēng)的半線性波動(dòng)方程初邊值問(wèn)題(1.1)-(1.3)的研究尚未得到完善.本文中, 我們考慮與文[12]中相同意思下的正則解與弱解且有以下主要難點(diǎn): 1) 當(dāng)p>2時(shí)無(wú)法利用對(duì)數(shù)-Sobolev不等式來(lái)估計(jì)對(duì)數(shù)所在的項(xiàng); 2)局部弱解的適定性無(wú)法直接導(dǎo)出, 需考慮更強(qiáng)的解的結(jié)果; 3)分析兩個(gè)非線性項(xiàng)之間的競(jìng)爭(zhēng)關(guān)系, 即基爾霍夫型非線性弱阻尼項(xiàng)與對(duì)數(shù)非線性項(xiàng)時(shí)遇到難度.為了克服這些困難, 啟發(fā)于文[2,13]的思想, 從問(wèn)題正則解的局部適定性出發(fā), 利用稠密性理論和緊性理論導(dǎo)出局部弱解的適定性.并通過(guò)修正能量泛函技巧將局部解推廣到了整體解.同時(shí)利用反證技巧, 得到具有負(fù)初始能量解的有限時(shí)刻爆破現(xiàn)象.
本文的剩余部分結(jié)構(gòu)如下: 第二節(jié), 我們將證明問(wèn)題(1.1)-(1.3)弱解的局部適定性; 第三節(jié)中, 給出當(dāng)p<γ時(shí)弱解的整體適定性.關(guān)于p>γ時(shí)具有負(fù)初始能量解在有限時(shí)刻發(fā)生爆破的結(jié)論, 在第四節(jié)中導(dǎo)出.
整文中, C及Ci(i = 1,···)在不同表達(dá)式中可能表示不同的正常數(shù).同時(shí), 記空間H :={u ∈(?):?u ∈L2(?)},且賦予內(nèi)積(u,v)H:=(?u,?v)+(?u,?v),其中(·,·)表示L2(?)的內(nèi)積.此外,(?)中的模取為∥?u∥2.
2.弱解的局部適定性
本節(jié)中, 我們將先證明問(wèn)題(1.1)-(1.3)正則解的存在唯一性, 之后, 通過(guò)稠密性理論得到局部弱解的存在唯一性.注意到, 得到弱解局部適定性之前, 先證明正則解的原因在于: 證明基爾霍夫型非局部阻尼項(xiàng)的收斂性時(shí), 需用正則解的一些結(jié)果.

由ODE標(biāo)準(zhǔn)理論可知, 上述Cauchy問(wèn)題(2.1)-(2.3)在區(qū)間[0,Tm),Tm> 0上存在唯一解bjm(t), 我們將通過(guò)接下來(lái)的先驗(yàn)估計(jì)將解延伸到[0,T].
第二步 先驗(yàn)估計(jì).


因此, 由(2.8)我們得到

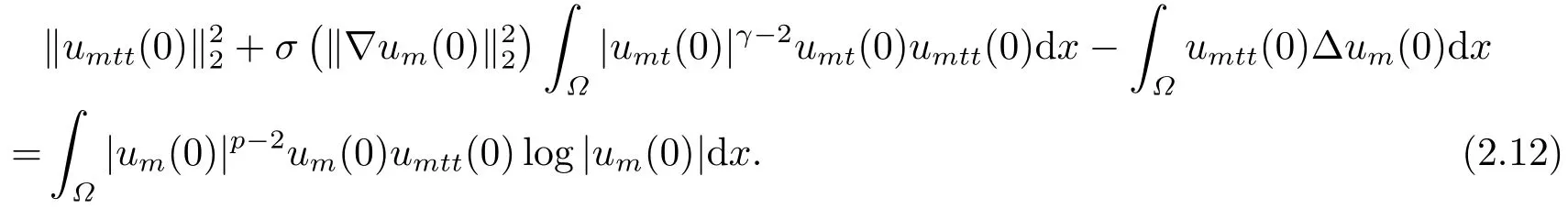
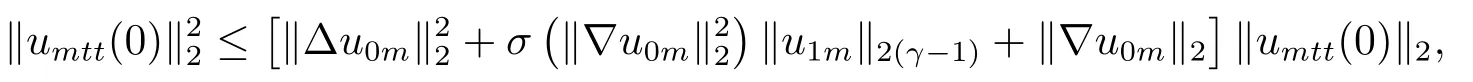
再由σ的連續(xù)性及(2.2), (2.3)可得

其中L2為與m無(wú)關(guān)的常數(shù).
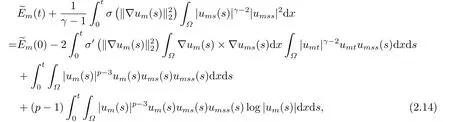
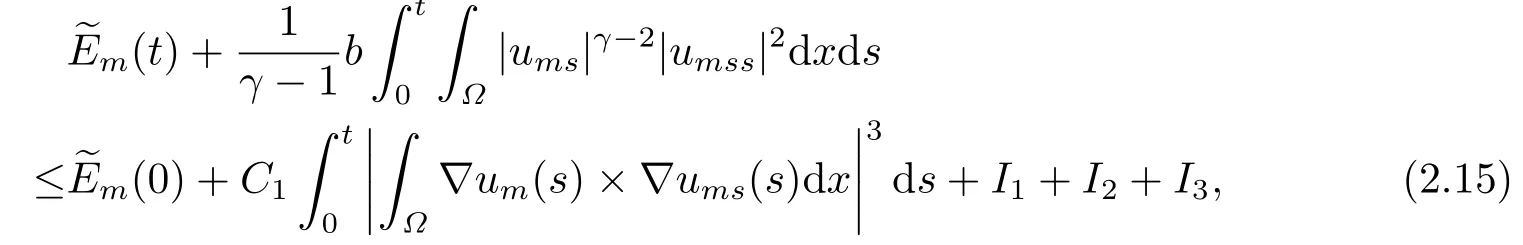
其中
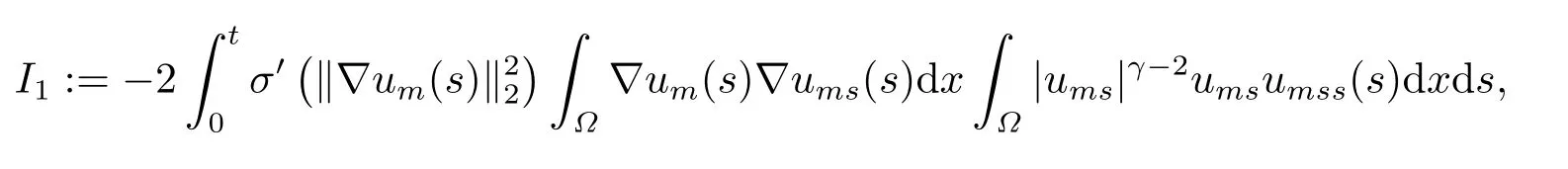

利用Young不等式, σ′的連續(xù)性及(2.9), 我們可以估計(jì)I1如下:


由(2.23), (2.24)及Aubin-Lions引理可得
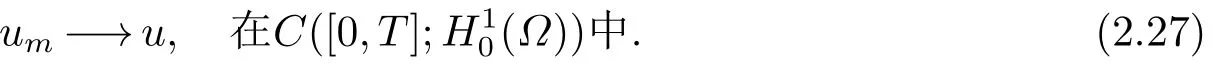
因此um?→u, a.e.(x,t)∈?×(0,T].這表明
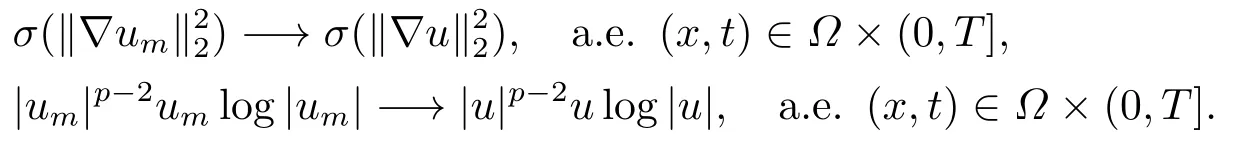
另一方面, 由(2.5), (2.9)及嵌入不等式, 我們導(dǎo)出
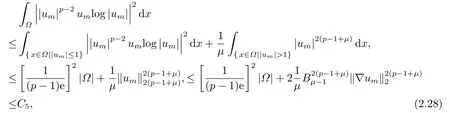
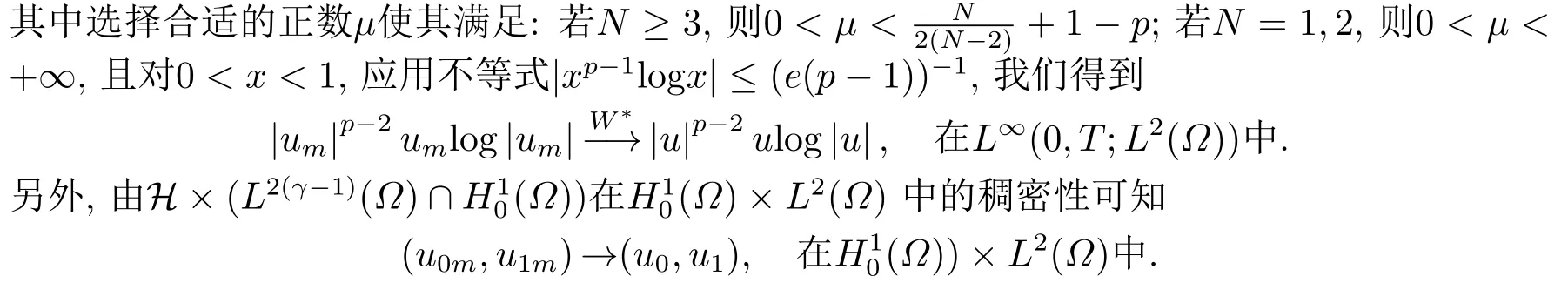
在(2.1)-(2.3)中取極限可得
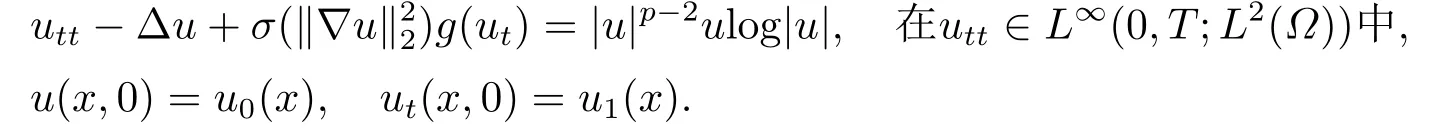
第四步 唯一性.令u1和u2是問(wèn)題(1.1)-(1.3)的解并記z :=u1?u2, 則由(1.1)我們可知z滿(mǎn)足如下的方程:
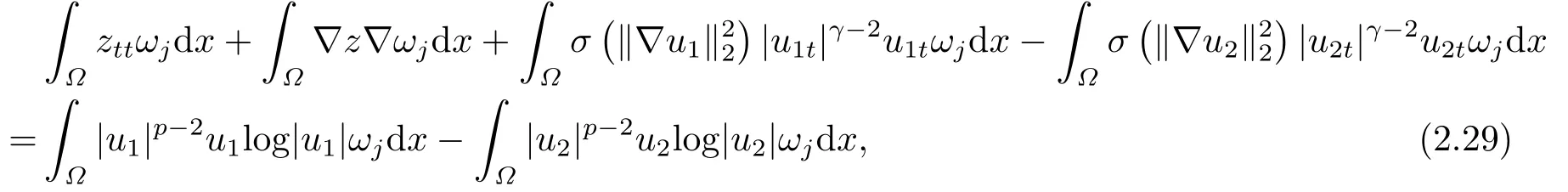
用zt代替上式中的ωj, 我們得到
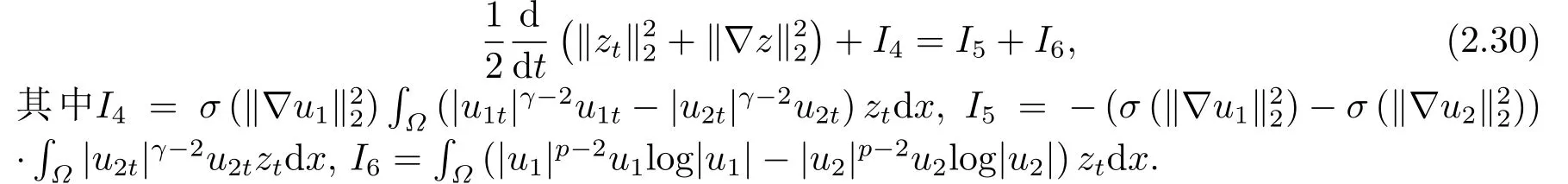
下面, 我們將估計(jì)I4~I(xiàn)6.首先, 應(yīng)用平均值定理, 存在θ ∈(0,1), 我們導(dǎo)出
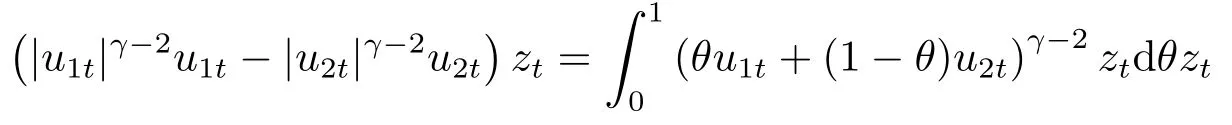
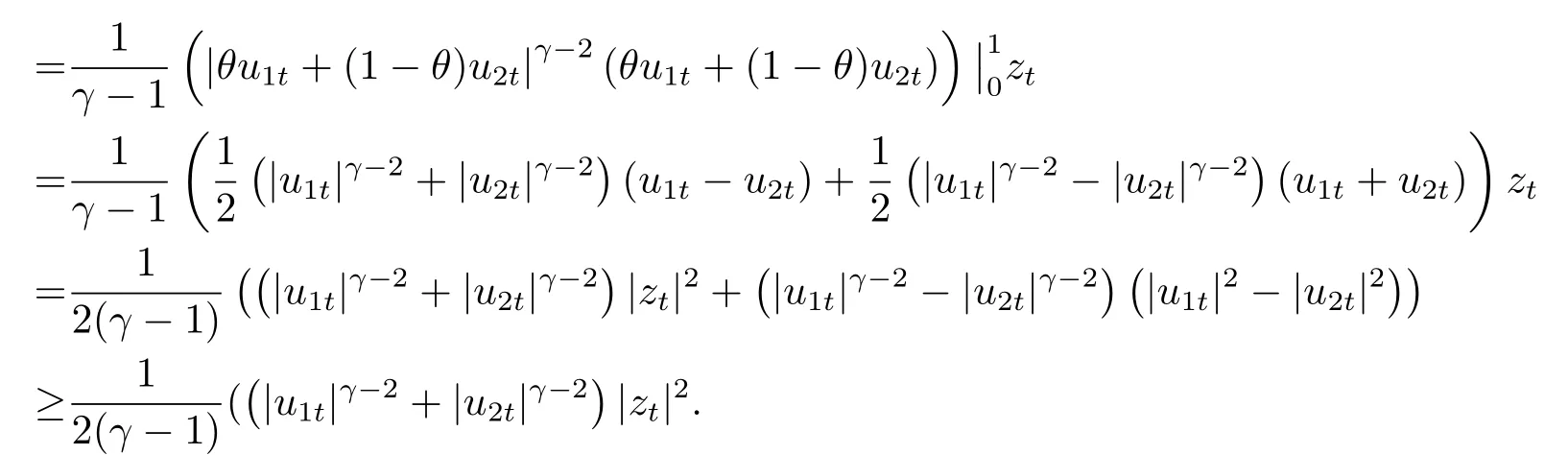
結(jié)合(H1), 我們可以對(duì)I4估計(jì)如下:
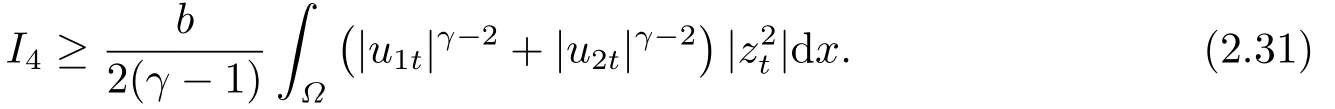
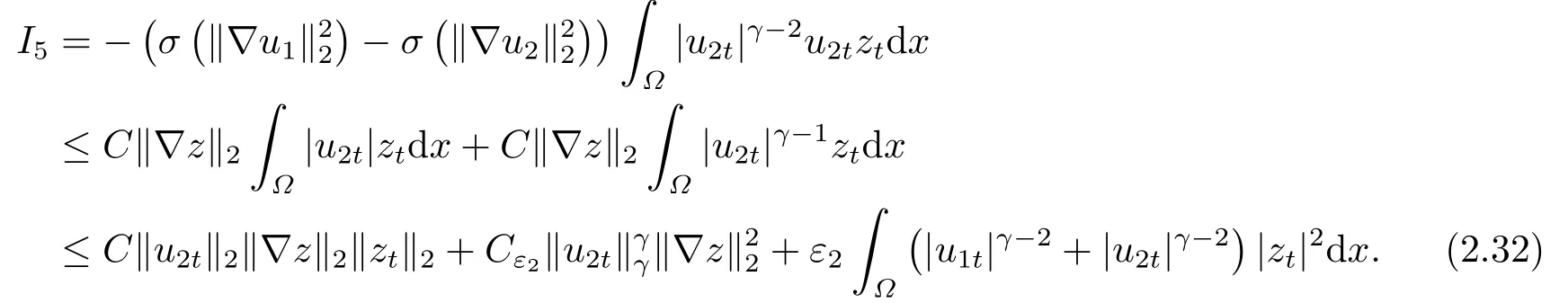
對(duì)I6, 用Hder不等式得到

其中G(s)=|s|p?2s log|s|.再由平均值定理及(2.5), 存在ξ ∈(0,1)使得
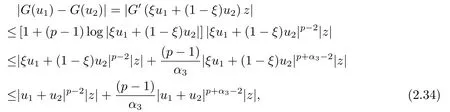

對(duì)上式從0到t上積分, 應(yīng)用(2.25)和Gronwall不等式, 可知存在正常數(shù)L4使得

且

因此, 以上收斂性并結(jié)合(2.28)允許我們對(duì)問(wèn)題(1.1)-(1.3)取極限, 且得到弱解滿(mǎn)足
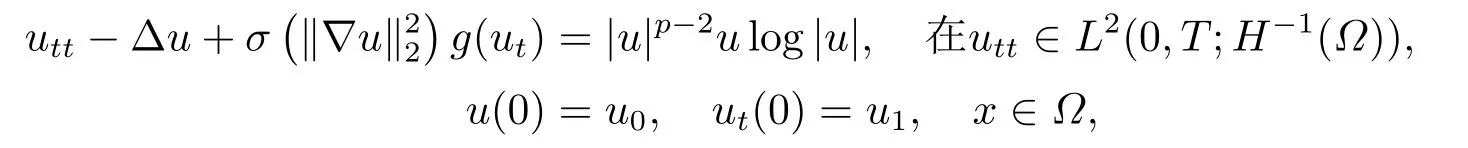
此外, 關(guān)于局部弱解的唯一性需要用正則化方法, 且可由Visik-Ladyzenskaya的標(biāo)準(zhǔn)方法來(lái)得到.[14]14?16綜上所述, 我們得到問(wèn)題(1.1)-(1.3)存在唯一的局部弱解.
注2.1局部弱解的唯一性不可用常見(jiàn)的唯一性證明方法的原因在于: 對(duì)偶積?H?1(?),L2(?)?沒(méi)有意義.
3.弱解的整體適定性
本節(jié)中, 當(dāng)p<γ時(shí), 結(jié)合連續(xù)性原理, 我們得到與第一節(jié)中的局部弱解相同正則性的意思下問(wèn)題(1.1)-(1.3)整體適定性.我們先給出下面引理, 將在證明中起到關(guān)鍵作用.


其中μ滿(mǎn)足適當(dāng)條件且我們只需證明F(t)滿(mǎn)足指數(shù)形式有界, 即通常的能量E(t)得到控制.

4.爆破現(xiàn)象
本節(jié)中, 我們利用反證技巧得到, 當(dāng)p > γ時(shí)問(wèn)題(1.1)-(1.3)具有負(fù)初始能量的解在有限時(shí)刻發(fā)生爆破.
引理4.1[11]若滿(mǎn)足則存在一個(gè)只依賴(lài)于?的正常數(shù)C使得下式成立
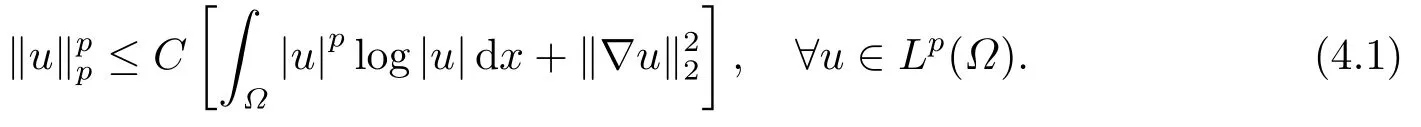
現(xiàn)在, 我們陳述有限時(shí)刻發(fā)生爆破結(jié)論.
定理4.1假設(shè)(H1), (H2)成立, p > γ且令(u0,u1) ∈?)×L2(?), E(0) < 0, 則問(wèn)題(1.1)-(1.3)的解在有限時(shí)刻發(fā)生爆破, 即Tmax<+∞.
證利用反證技巧, 假設(shè)問(wèn)題(1.1)-(1.3)解整體存在, 即Tmax=+∞.我們引入輔助函數(shù)
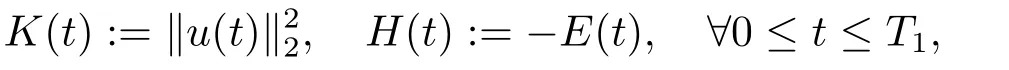
其中正常數(shù)T1將在之后給出.且由E(t)的單調(diào)性可知: H′(t)=?E′(t)≥0, 且
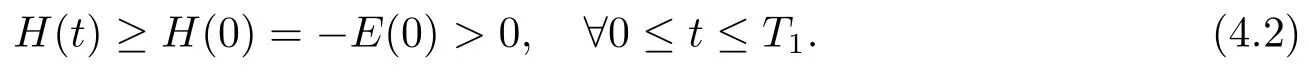
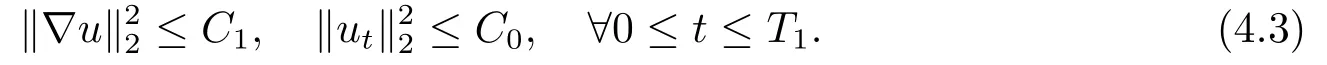
并由條件(H1)中σ(s)的連續(xù)性, 我們有
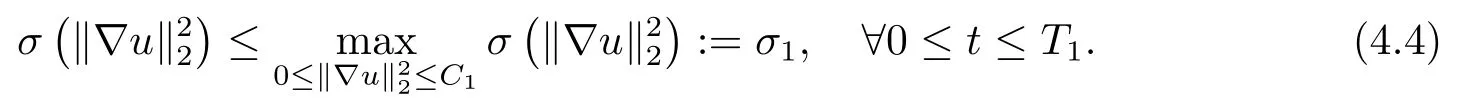

其中正常數(shù)η將在之后給出.
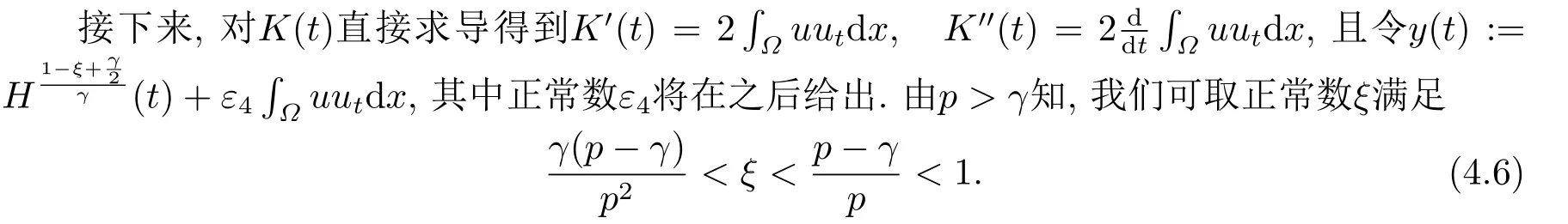
且對(duì)y(t)直接求導(dǎo), 并利用(4.5)式, 我們有
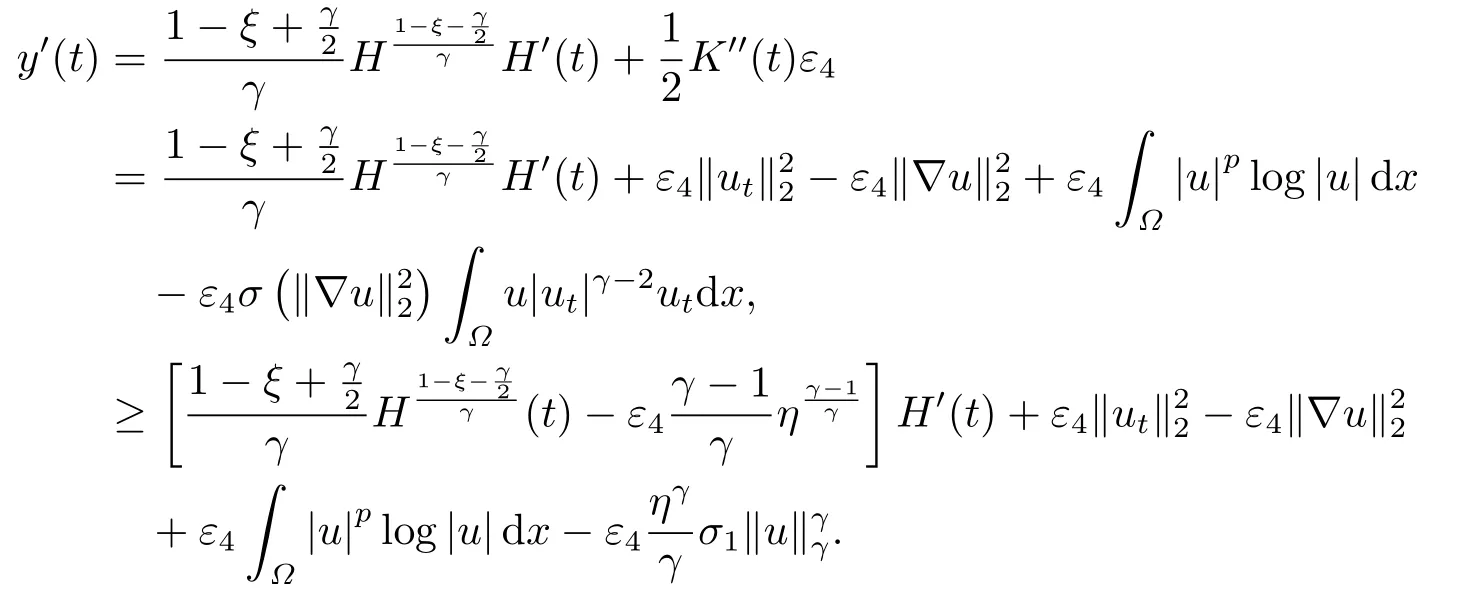
進(jìn)一步, 引入0 且引理4.1的條件成立. 下面, 我們估計(jì)(4.7)式右端最后一項(xiàng).由引理4.1可得 并結(jié)合(4.2)和Young不等式, 我們導(dǎo)出 將上式代入到(4.7)并整理得到 此外, 應(yīng)用(2.5), (4.3), H(t)的定義和嵌入不等式, 我們得到 且上式與(4.2)和(4.10)結(jié)合, 我們導(dǎo)出 其中最后一式由(4.12)得到.顯然, (4.17)與(4.18)產(chǎn)生矛盾且我們知Tmax<+∞.定理4.1證畢.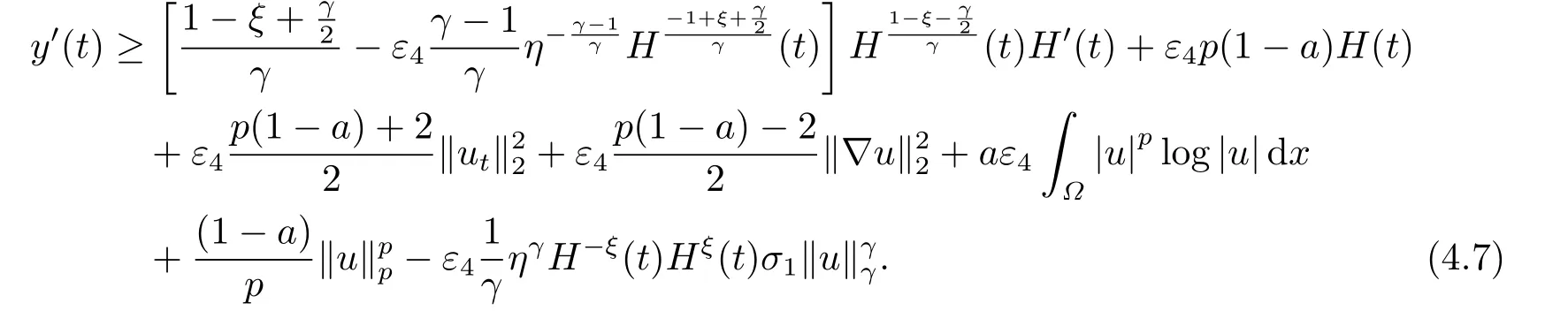

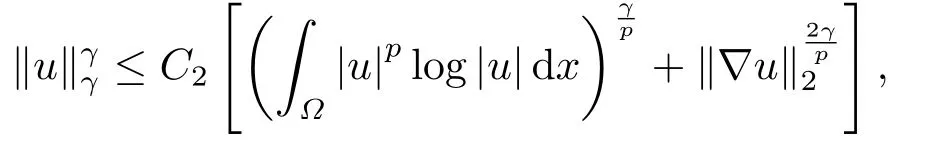
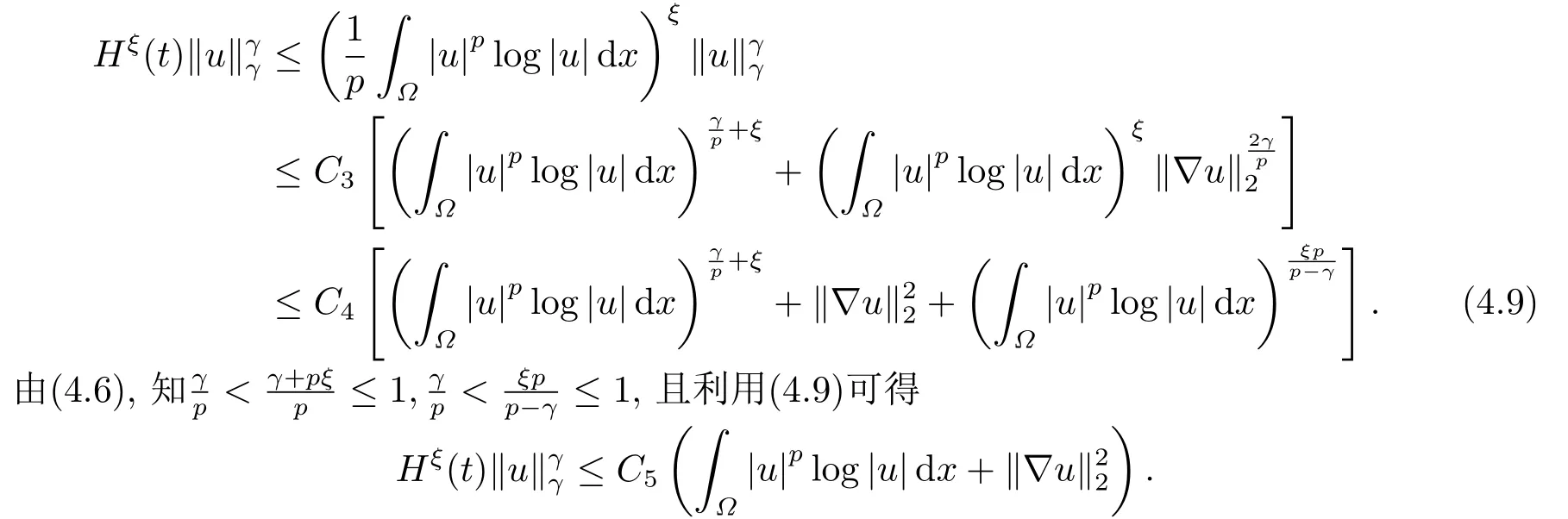

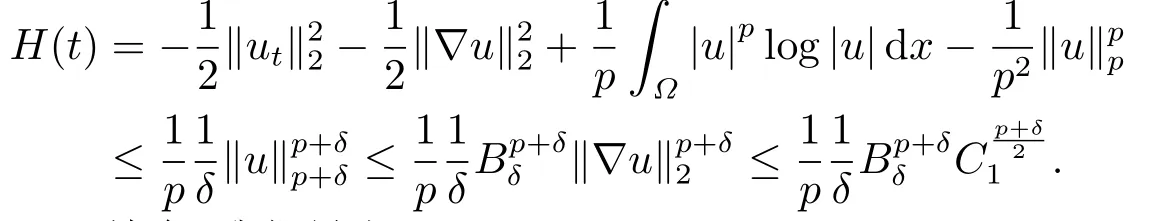


- 應(yīng)用數(shù)學(xué)的其它文章
- 一類(lèi)基于心理作用的隨機(jī)SIRS傳染病模型
- 一類(lèi)帶邏輯脈沖線性系統(tǒng)的最優(yōu)控制問(wèn)題
- 線性半向量二層規(guī)劃問(wèn)題的割平面方法
- Existence and Uniqueness Theorems of Almost Periodic Solution in Shifts δ±on Time Scales
- Higher Derivative Estimates for a Linear Elliptic Equation
- A Note on the Distance Signless Laplacian Spectral Radius

