Federated Reinforcement Learning with Adaptive Training Times for Edge Caching
Shaoshuai Fan,Liyun Hu,Hui Tian
State Key Laboratory of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China
Abstract: To relieve the backhaul link stress and reduce the content acquisition delay, mobile edge caching has become one of the promising approaches.In this paper, a novel federated reinforcement learning(FRL)method with adaptive training times is proposed for edge caching. Through a new federated learning process with the asynchronous model training process and synchronous global aggregation process,the proposed FRL-based edge caching algorithm mitigates the performance degradation brought by the non-identically and independently distributed (noni.i.d.)characteristics of content popularity among edge nodes. The theoretical bound of the loss function difference is analyzed in the paper, based on which the training times adaption mechanism is proposed to deal with the tradeoff between local training and global aggregation for each edge node in the federation. Numerical simulations have verified that the proposed FRL-based edge caching method outperforms other baseline methods in terms of the caching benefit, the cache hit ratio and the convergence speed.
Keywords: edge caching; federated reinforcement learning (FRL); non-identically and independently distributed(non-i.i.d.)
I. INTRODUCTION
With the augmentation of nascent services and user equipment(UE),the networks need enhanced service capabilities with the lower request response time. To tackle the massive data requests,mobile edge caching becomes one of the promising methods. In an edge caching system, the edge nodes are equipped with communication, computation, and storage capabilities, which predict and cache the potential popular content in advance. In this way, the UEs can directly obtain the requested content rapidly at the edge of the network. The edge caching method has been studied extensively in the literature.Traditional cache replacement strategies such as the least recently used (LRU)and the least frequently used (LFU) have been used by a lot of research work [1, 2]. However, due to the increasing data and the enhancing dynamic environment, it becomes more difficult for the traditional methods to adapt to the dynamic content popularity in time without exploiting any content popularity information[3].
In order to figure out the edge caching problem in a dynamic environment, using the reinforcement learning(RL)based edge caching method to track the content popularity trends becomes one of the promising research directions [4, 5]. Recently, studies have applied RL methods to a single BS in diverse edge caching scenarios to achieve different caching goals[6–9]. In[6],a Q-learning based edge caching method is proposed in the heterogeneous network with the purpose of minimizing the caching cost. In [7], the use of the natural actor-critic learning method is studied to tackle the joint caching,computing,and radio resource allocation problem in fog-enabled IoT networks. In a general mobile edge computing network with multiuser and multicast data,a hierarchical reinforcement learning method is proposed in [8]. The aim of the method is not only to maximize bandwidth utilization but also to decrease the total quantity of data transmitted. In[9],the authors consider the proactive caching problem in wireless networks with the aim of minimizing the long-term average energy cost of delivering content to the UE over a time-varying wireless link,and a reinforcement learning-based method is applied to solve the problem.
Although RL-based caching methods for a single BS can be applied to multiple scenarios and adapt to diverse goals, the learning efficiency can be further improved. The distributed caching model training between BSs is one of the effective directions [10–12].In [13], a multi-agent Q-learning based edge caching framework is proposed to find the optimal caching policy. Due to the large size of the state and action space,it is difficult to maintain the Q-value for each action.The researchers in[14]proposed a multi-agent actorcritic learning-based edge caching mechanism,where each actor(i.e., BS)makes its own decision independently while a critic node is applied to estimate the whole reward.In the distributed framework,the global critic node only evaluates the caching policies of each actor respectively without further cooperation.In[15],a multi-agent actor-critic learning-based cooperative edge caching framework is proposed. In the framework, a communication module is introduced to extract and share the variability of the actions and observations of all BSs.Besides,the global critic network is applied to evaluate the caching policies of BSs based on the global state, caching actions, local states, and rewards in BSs. Nevertheless,the interactive information among BSs increases the transmission burden and risks to the backhaul links,and it takes a long time for model learning process.
In this regard, the federated learning (FL) method emerges as a promising method,where BSs in the federation train local models with decentralized data samples without exchanging the actual data or state information [16, 17]. Besides, the model learning time is shortened due to the shared model information. Since first proposed in [18], the FL method has shown its effectiveness through experiments in a variety of applications, ranging from medical to IoT, transportation, defense, and mobile apps [16, 19]. In a federated framework,the edge BSs together with an aggregation node (AN) act as a federation to perform the learning processes. The AN updates the global model parameters based on the uploaded local models. In this way,the request data of users are kept in each BS,thus ensuring the data privacy[18,20,21]. Moreover,the encryption process of the model information transmission in the FL mechanism further ensures the data privacy [21]. However, since the encryption process has no impact on the research of the paper, it is not described in detail. Besides, the local model training makes the computation abilities of edge BSs effectively utilized [22]. The FL methods have already been applied to edge caching scenarios. In [23], a federated deep-reinforcement-learning-based cooperative edge caching(FADE)framework is proposed to cope with the challenge of offloading duplicated traffic. FADE federates all local UEs to collaboratively train the parameters and feed them back to the BS to accelerate the overall convergence speed [23]. In the Internet of Things(IoT)system,a blockchain-assisted Compressed algoRithm of fEderated leArning is applied for conTent caching(CREAT)to predict content popularity and make caching decisions [24]. However,these studies take a fixed training frequency and a common model for a federation based on the assumption that the training data for edge nodes are independently and identically distributed. Although the proximity in areas gives the similarities in content popularity characteristics(CPCs)of BSs,the diversity of user preferences in different coverage areas leads to different local CPCs of BSs. The non-identically and independently distributed (non-i.i.d.) characteristics of content popularity among edge BSs becomes a significant problem to be addressed.
In the paper,we focus on the problem of how to efficiently federate the edge nodes and perform caching control algorithms given the non-i.i.d. characteristics among edge BSs. A federated reinforcement learning (FRL) method with adaptive training times for edge caching is proposed. In the FRL-based edge caching method,the asynchronous model training process and synchronous global aggregation process are proposed to reform federated learning. Specifically,in the proposed FRL framework, each BS in the federation trains its local model for diverse times asynchronously, while each BS sends the latest model to the AN synchronously. Then all BSs in the federation wait for the global aggregation process to be performed, obtain the updated global model from AN,and select from the global and local model. Additionally, the RL method is applied to each BS to control local caching, while the FL framework is applied to an edge federation to share the learning experiences to speed up the converging process. The main contributions in the paper are as follows:
? In edge caching scenarios with non-i.i.d. content popularity,the caching control process is established by the Markov decision process(MDP)model. To solve the MDP problem, the FRLbased method is applied under the designed caching benefit considering the cache update cost and the fit between the cached content and the content popularity.
? To address the non-i.i.d. characteristics of content popularity between edge BSs,a novel FL algorithm is proposed. In the novel FL algorithm,each BS has a model selection process to choose the better caching model between the local updated model and the global aggregated model for satisfying the diverse content popularity users in its coverage area. Besides, the global model is aggregated based on the diverse characteristics of uploaded local model between BSs,including the data amount for local training,and the correlation between the global model and the local model,reflected by the latest time that the global model is locally adopted.
? Based on the comparison between synchronous and asynchronous method of distributed gradient descent in [25], it is analyzed in [18] that federated learning should use the synchronous update approach because it is more efficient than asynchronous approaches. In the proposed learning process, BSs in a federation keep the same FL model decision pace but different training pace.To some extent, more training leads to a higher model fitting accuracy, but shorter user requests collection intervals and less accurate content popularity. Both model fitting accuracy and data accuracy influence the convergence value of the caching benefit. To balance the tradeoff between model fitting accuracy and data accuracy, a solution to the adaptive number of training times per every model decision period is proposed,based on the derived theoretical bound of the loss function difference.
The rest of the paper is organized as follows. Section II introduces the general mobile edge system model of the caching problem. Section III formulates the edge caching problem including the caching control problem,learning problem,and the training times adaption problem. The FRL-based edge caching control algorithm is proposed in Section IV. The simulation results are included and analyzed in Section V followed by the conclusions in Section VI.
II. SYSTEM MODEL
In this section,we first introduce the edge caching system with sandbox subsystems. Next, the federated learning model for edge caching is presented. Some key parameters are listed in Table 1.

Table 1. Key parameters for FRL-based edge caching method.
2.1 Edge Caching System with Sandbox Subsystems
In the edge caching system, each BS collects the requests from user equipment in its coverage area and serves users directly through the local cache. Considering the limited caching capabilities of BSs, the caching storage denoted asMin each BS is much smaller than the amount of content denoted asFin the whole system, i.e.,M ? F. If the requested content is not stored locally, the BS uploads the requests to the core network and waits for the content to be sent back via backhaul links. Take the model selection interval as a round. For roundk(k ∈ {1,2,3,···}), the caching state in a BS is denoted as, where pg[k],pl[k] are the global and local content popularity characteristics respectively, and a[k] is the real caching action at roundk. pl[k] is aF ×1 vector of local content popularity profile for the coverage area of the BS. Thereinto, thef-th entry reflects the request frequency of contentfwithin local coverage area in roundk, as given by [pl[k]]f=. Likewise,pg[k] denotes content popularities in coverage areas of the whole federation. The action matrix for roundkis a[k]∈A, whereAis the set of all the feasible actions defined asA={a|a∈{0,1}F,aT1 =M}.af[k] = 1 indicates that contentfis cached at roundk. Otherwise,contentfis not cached at roundk. The caching action shows the state of the storage unit of the BS at the current round,namely the current stored and unstored requested content.Therefore,the caching action acts as part of the caching state. Each BS obtains the caching action for the next round based on the current caching state. The caching action at roundk+1 is acquired as a[k+1]=π(s[k]),whereπ(·):S →Ais the caching policy learned by the ML method. Considering the computing ability of each BS, the federated learning framework is deployed on multiple BSs to make the computing ability fully utilized. Based on the federated learning framework,each BS in the federation is able to perform the caching model training,thus improve the learning efficiency.
Note that the introduction of machine learning(ML)techniques to networks may raise concerns regarding transparency, reliability, and availability. Even if the performance of networking systems can be improved by ML techniques in the long term,it is safe to assume that the system will unavoidably experience certain performance degradation during a transitory regime.Out of the concern that ML methods may generate instabilities to networking systems,the sandbox subsystem is first proposed by ITU-T[26],in which the ML models are sent to the sandbox for training, testing,and evaluating before being deployed in real environments.In this paper,the idea of the sandbox is adopted in our considered caching system, where each edge node contains a sandbox. The sandbox performs the virtual training process before making the real caching decision,thus the model training and learning process can be accelerated.
In each BS, there is a caching control unit (CCU)and a storage unit (SU). The CCU stores the learning model and determines the caching policy based on the model. The SU stores the selected content based on the caching policy. To execute the virtual training based on the real-time data,the sandbox also includes a CCU and a SU. For convenience, the CCU in the sandbox is denoted as the virtual CCU (vCCU) and the SU is denoted as the virtual SU (vSU). Similarly,the vCCU is responsible for storing and updating the virtual training model obtained in the sandbox. Meanwhile,the vSU stores the selected content virtually according to the caching policy performed in the sandbox. In roundk, the sandbox completes the virtual training based on the content popularity distribution collected in the data acquisition interval for the virtual training process. After the virtual training process,the sandbox sends the newly updated training model in the vCCU to the CCU,which compares the model with the global model and decides whether to adopt the model later.Figure 1 depicts the training module architecture in a BS.
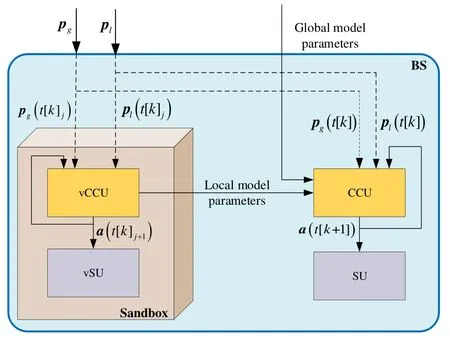
Figure 1. The architecture of the training module in a BS.
2.2 Federated Learning Model
In this paper,federated learning is adopted for the edge caching decision for multi-BS systems.The FL framework includes an AN and several BSs. The learning process of a federation is controlled by the AN,which is a logical component that can run on the remote cloud, or an edge node[19]. In each round, the federated learning process is mainly composed of four steps, namely, training times computation, local virtual training, global aggregation, and parameter decision. The duration of each round is denoted asT,therefore, the local virtual training interval is determined by the number of virtual training times computed at the beginning of each round.For BSi,the virtual training interval in roundkis represented byτi[k].Each virtual training process consists of data acquisition intervaland model training interval,i.e.,changes in pace withτi[k],whereasis determined by the computing abilities of the CPU. Due to the dynamic content requests, it is necessary to analyze the current content popularity based on request data in close time and make the learning caching mechanism adaptive to the dynamic changes of content requests. For roundk, a possible time scheduling is depicted in Figure 2. As Figure 2 shows, the beginning time of roundkis represented byt[k],followed by the virtual training intervals. The virtual training times of different BSs in the roundkare different, and the corresponding data acquisition intervals are diverse accordingly. For convenience,the beginning time of thej-th virtual training for BSiin roundkis denoted ast[k]j.

Figure 2. An example of the time scheduling for round k.
The federated learning process in a round is depicted in Figure 3. The four steps of the federated learning process are analyzed as follows.
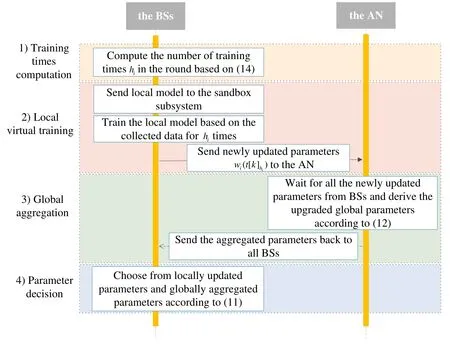
Figure 3. The federated learning process in a round.
1) Training times calculation:In the FRL-based edge caching algorithm,virtual training is implemented in the sandbox subsystem based on user requests accumulated in a virtual training interval. The number of virtual training in every local BS influences the convergence speed and the convergence value because of the tradeoff between model fitting accuracy and data accuracy. At the beginning of each round, the number of virtual traininghi[k]is calculated,which guides the following local virtual training. The duration of training times calculation is negligible compared with the duration of virtual training.
2) Local virtual training:Each BS sends its local caching model to the sandbox subsystem. Based on the training times calculation, the caching model ofi-th BS is trained forhi[k] times in the sandbox. In each virtual training,the BS collects the user requests and sends the content popularity characteristics to the sandbox subsystem. Based on the content popularity information the sandbox subsystem trains the local caching model and obtains the virtual caching action. The BS does not perform the cache deployment based on the virtual action, which is simply applied to optimize the caching model. The updated caching model parameter gradients are output to the BS, which updates its local parameters and uploads the parameters to the aggregation node.
3) Global aggregation:The AN maintains a global caching model for the federation.In the global aggregation step, the AN gathers the model parameters from all BSs,integrates the parameters,and upgrades the global model, which will be transmitted to all BSs in the federation later. Set the global parameters as wgand the local model parameters in BSias wi. The global aggregation process can be denoted as,whereξiis the weight of the model parameters in BSi.
4) Parameter decision:The upgraded parameters from AN are not meant to be better than local updated parameters due to the non-i.i.d. characteristics of BSs. BSs may choose the local model because the local model might be more suitable for local content requests. Therefore,the parameter decision is scheduled at the end of a round for each local BS to choose a more effective caching model. Then the chosen model will be applied to perform the real caching process and the learning process in the next rounds.
III. PROBLEM FORMULATION
In this section, we formulate the caching control process as a Markov decision process (MDP), aiming to maximize the caching benefit with the consideration of the caching cost and rewards. In this way,the FRL algorithm is able to be applied to the considered edge caching scenario. Considering that the tradeoff between model fitting accuracy and data accuracy influences the federated learning performance,the training times adaption problem is formulated.
Due to the temporal correlations,the content popularity dynamics can be modeled using Markov chains[27].The Markov chains are adopted to model content popularity dynamics at both global and local scales.For BSi,si(t[k]j)represents the caching state of thejth local virtual training in roundk,while si[k]denotes the caching state of roundk. For convenience,we use si(u)to refer to si(t[k]j)or si[k]due to the similarity of virtual training process and real caching process,in which state si(u)is only influenced by si(u?1)rather than any other previous states of BSi,and the real/virtual caching decision can be made according to si(u).In the caching control process, the caching action selected in time intervaluconstitutes part of the next state si(u+1). Hence, the above optimal sequential decision-making problem under a stochastic environment can be formulated as the Markov decision process(MDP).
To evaluate the benefit of caching action,we define the caching benefit asB. Similarly, we useBi(u) to refer toBi(t[k]j) orBi[k]. Considering the caching cost and the rewards for the fit between cached files and requested content,the caching benefitBi(u)is set as
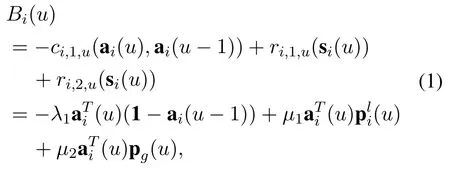
whereλ1,μ1,μ2denote the weights of three different summands and(u), pg(u) represents the local and global content popularity characteristics. Thereinto,ci,1,u(ai(u),ai(u ?1))denotes the cost of caching the contents which are not cached in time interval(u ?1)(roundk ?1 or the(j ?1)-th virtual training in roundk). Meanwhile,r1,u(si(u))andr2,u(si(u))denote the rewards for the match between the caching action and the local and global content popularities,respectively.
Note that the performance of the caching policy is evaluated by the state value function as
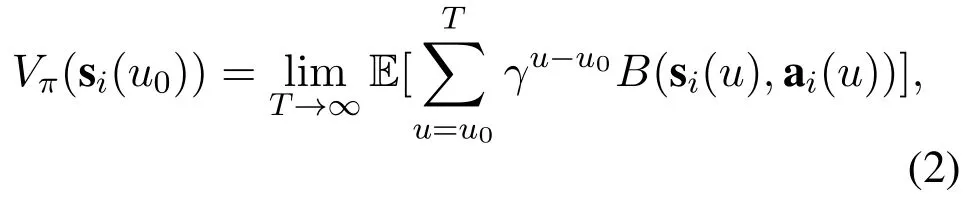
which shows the total reward from the current state to an infinite state,counted by the factorγ ∈(0,1).
Based on the state value function defined in Equation(2),the optimal caching policycan be defined as
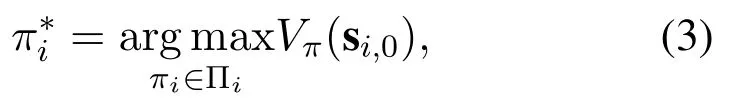
where si,0is the initial state of BSiin the edge system,and Πirepresents all feasible caching policies for BSi.
By Bellman equations,Equation(2)can be rewritten in a recursive form as

The goal of the MDP is to obtain the optimal caching policy as,under whose guidance the maximum of the caching benefit is attained in every caching state. Namely,the state value function is given by
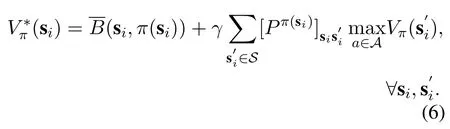
Clearly,the solution to Equation(6)depends on the state exchange probabilitywhich is not available in practice. Therefore, the federated reinforcement learning is applied to attainandV ?(si)without knowing the apriori.
While federated learning is applied to learn a common model for nodes in the federation, actor-critic learning is employed to train and learn a local model for each node in the federation. The actor-critic learning framework contains two different networks,i.e.,an actor network and a critic network.
On the one hand, the caching policy for BSi,denoted as, is derived in the actor system. For each time intervalu, the caching policyindicates the probability of taking action ai(u)at caching state si(u). The loss function of actor network is a cross-entropy function, as given by
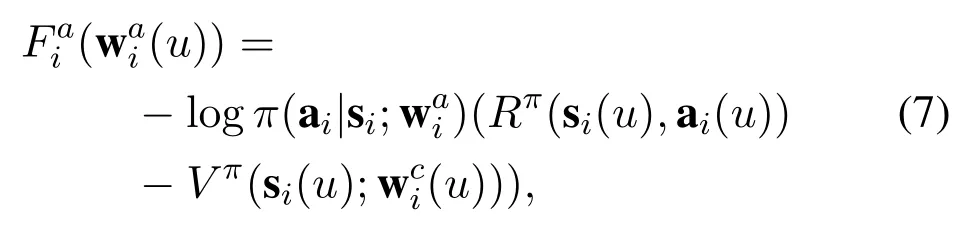
On the other hand, the critic network provides an assessment mechanism to evaluate the obtained policy. The learning objective of the critic network is to minimize its loss function,thus obtaining the pertinent state value function and guiding the optimization of policy in the actor network. The loss function of critic network is a mean squared error (MSE) function, as given by
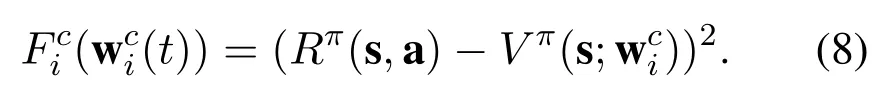
It can be seen from Equation(7)that the state value function acquired by critic network influences the loss function of actor network, thus the update of model parameters in actor network.For convenience,the loss function of critic network in thei-th BS is denoted asFi(wi). Hence, the learning objective of each edge node is to find
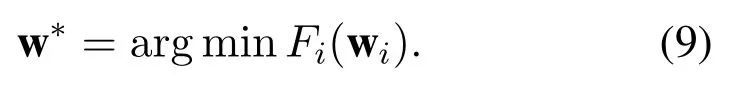
In the proposed edge federated learning framework,BSs collect the local and global content requests data and make caching decisions based on the proposed actor-critic learning-based edge caching method. The request data accuracy is judged by the arriving amount of request data in time instanceu, considering that a large amount of data depicts the content popularities more accurately. As Figure 2 shows, there is a tradeoff between virtual training and data accuracy. For machine learning, massive training based on accurate data tends to achieve good learning results.In a round,more virtual training times means shorter data acquisition periods, which restricts the amount of arriving data so that the data is more accidental and its statistical property is less accurate. Therefore, the problem of how to seek the tradeoff between model training and data collection in the edge caching scenarios is deserved to be studied.
Suppose there areNedge nodes in the federation.We define the arrival number of user requests in BSiduring all virtual training in roundkasDi[k] =represents the arrival number of user requests for thej-th virtual training. On the one hand,more training leads to a higher model fitting accuracy,i.e.,the model is more suitable for request data. On the other hand, for a model decision period, more training leads to shorter user requests collection intervals and less accurate request data. Taking both factors into consideration,the problem of training times adaptation is delineated as follows.

wherehmaxis the max number of training times per round. Besides, wi(t[k+ 1]) denotes the caching model parameters in thei-th edge node at the beginning of the(k+1)-th round,whiledenotes the optimal caching model parameters.Fi(w)is the loss function of critic network in thei-th node.is the difference between the loss function in thek+ 1 round and the optimal loss function value, which reflects the model fitting accuracy.Meanwhile, the data arrival numberDi[k] represents the data accuracy in roundk, which reflects the indirect influence between the number of training times and the convergence. Moreover,αis the weight parameter.
IV. FRL-BASED EDGE CACHING ALGORITHM
With the focus on the non-i.i.d. characteristic of BSs,the parameter selection & global aggregation processes are proposed in the section. Next, the solution to the training times adaptation problem is presented.Finally,the FRL-based edge caching algorithm is proposed and analyzed.
4.1 Parameter Selection & Global Aggregation
Federated learning is applied to excavate the commonness for the federation.However,the non-i.i.d.characteristics between BSs make the global model unable to fit the local user requests perfectly. To solve the problem, the model selection process is set at the end of each round. Each BS selects a set of parameters from the global aggregated model and local updated model to satisfy users in their coverage areas. After receiving the global parameters, each BS in the federation compares them with local parameters through the loss function. In other words, the model in each BS is selected separately by evaluating the performance of the two sets of parameters in the local user request data as
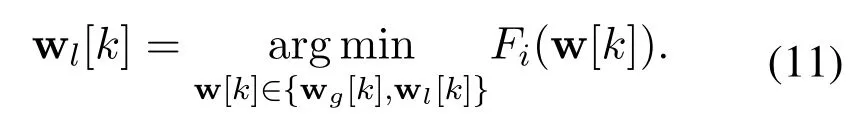
Besides, the federation exit mechanism is designed to further ensure the adaptation of the caching model to the local user requests. The federation exit mechanism means that the BSs will withdraw from the federation and perform the local model training independently when they do not choose the global model for a long certain period. In this way,each BS can finally obtains the convergence of the caching model based on the local requests.
Figure 4 illustrates an example of model selection and local model training process. The blue diamond represents the round that the BS selects the global aggregated model. The color of these blue diamonds delineates the number of virtual training for a local BS model in the round. The darker color indicates more virtual training for the BS in the round. The yellow arrow represents the duration from the latest round the global model was adopted to the current round. Note that,if a BS did not choose the global model for a long time,the model updated locally is more suitable for local user requests and is unable to provide other BSs in the federation with valuable experience. Hence, the BSs with the recently received global model tend to take a more significant role in the global model aggregation process. Consequently,considering the data amount and the latest time the global model is adopted,the global aggregation parameters can be designed as
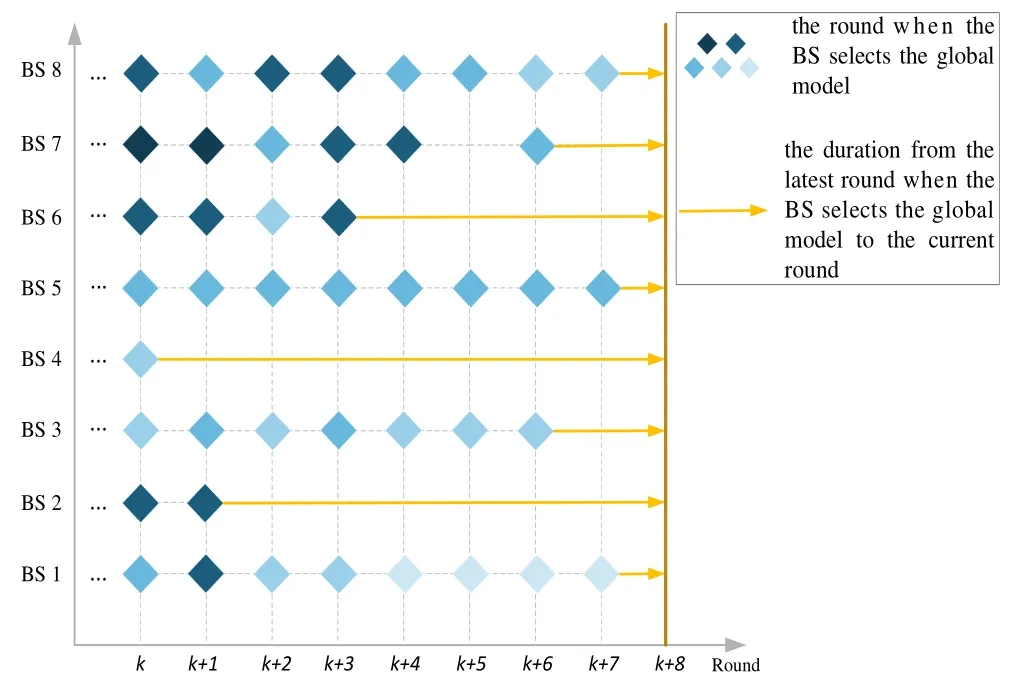
Figure 4. An example of model selection and local model training process.
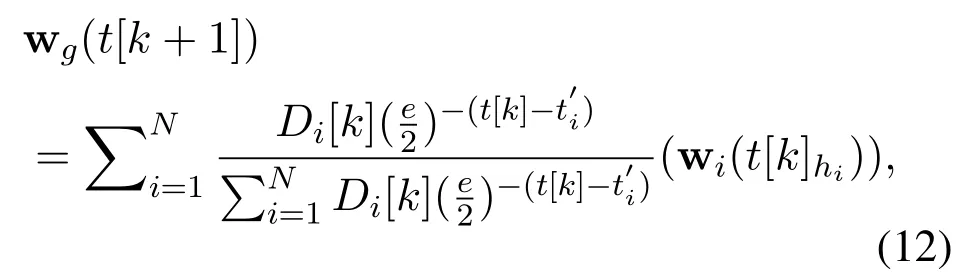
whereD[k]is the total user requests arrival number in the federation,eis the natural logarithm used to depict the time effect[29],andis the receiving tag,which shows beginning time of the latest round when BSiselected the global model parameters.
4.2 Derivation of Training Times in A Round
As mentioned in Section III, the adaptive number of training times in each round is a problem to be addressed, in order to balance the virtual training process and data collection. To prevent the invalid data problem caused by the small data acquisition period,the maximum number of training times in a round for the federation is set ashmax. For the analysis of the loss function, some assumptions have been made to the loss functionFi(w)in BSias follows[19].
Assumption 1.Fi(w)is convex.
Assumption 2.Fi(w)is β ? Smooth, i.e.,∥?Fi(w1)??Fi(w2)∥ ≤ β∥w1?w2∥for anyw1,w2.
Assumptions 1 and 2 are satisfied for the linear regression model, whose loss function is MSE function [19]. Based on the research in [19, 30–33], the derivation also works well for the neural network-based models. Additionally, for roundk ∈{1,2,··· ,K}, we define the loss function difference, whereindicates the optimal model parameters of BSi.
According to the convergence bound of gradient descent given in [34],θi[k]>0 is always satisfied.For the parameter selection process in a round, each node will choose model parameters from the local update and global aggregation parameters based on the loss function values. Therefore,there are two possible cases as Figure 5 shows.
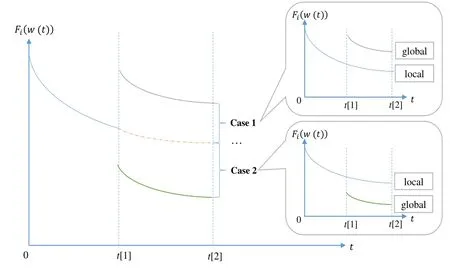
Figure 5. Illustration of parameter selection process.
Case 1.The local update model is better than global aggregation model. As shown by the curve 1) in Figure 5, the loss function of local update model is smaller than global model. Here the BS i employs the local update model parameters, i.e.,wi(t[k]) =And the loss function difference θi[k]satis-.
Case 2.The global aggregation model is better than local update model. As shown by the second curve 2) in Figure 5, the loss function of global distribution model is smaller than local model. Here the BS i employs the global integration model parameters,i.e.,wi(t[k])=wg(t[k]). And the loss function difference θi[k]satisfies θi[k] =Fi(wg(t[k]))?Fi()≤Fi((t[k]))?Fi().
Hence, conditionθi[k]≤Fi((t[k]))?Fi()is always satisfied. As a consequence, we have the following theorem.
Theorem 1.For any round k ∈ {1,2,··· ,K},we have, and? satisfies Fi(wi(t[k]))?Fi(wi(t[k+1]))≥?>0.Proof.We first obtain an upper bound ofFi(wi(t[k+1]))?Fi(wi(t[k])) for each nodei, based on which the final result is attained. For details, see Appendix A.
Based on Theorem 1,θi[k]satisfies
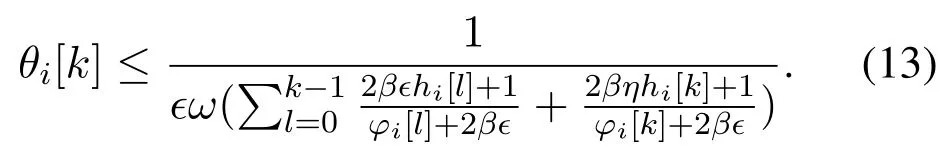
Substituting Equation(13)into Equation(10),we have
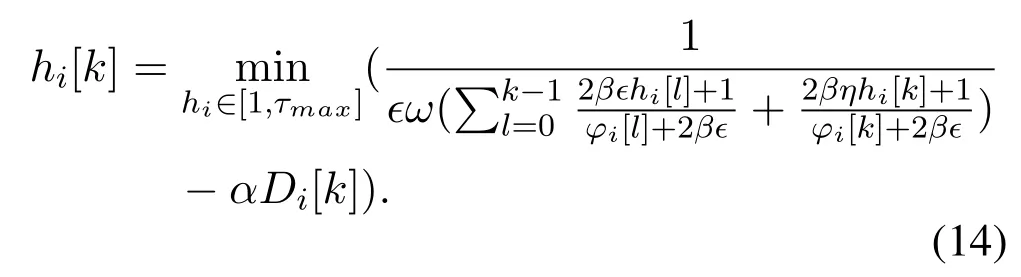
Thus each BS in the federation is able to adaptively obtain the number of training times for a round based on the arriving number of user requests as Eq.(14).
Algorithm 1 depicts the caching control process in BSi. In Algorithm 1, some steps such as global aggregation and adaptive virtual training times in each round are proposed for better learning performance.After the initialization steps,the algorithm repeats the four steps in the federated learning process, as described in Section II.B.At the beginning of roundk,BSicalculates the training times of roundk,see Lines 5-7. Then, the virtual model training is performed as Lines 8-16. The selected model is trained forhi[k]times,and the newly updated model is uploaded to the AN, which will perform the global aggregation process according to Eq.(12). At the end of roundk,BSicompares the global aggregated model and the local updated model and selects the model with a smaller loss function of critic net,see Lines 19-26.
V. SIMULATION RESULTS AND ANALYSIS
In this section,we evaluate the performance of the proposed FRL method with adaptive training times for edge caching through numerical simulations.The simulations are carried out in an edge caching scenario where 8 BSs are considered as a federation. Three sets of the parameters of the incurred benefits are considered as: (Z1)λ1= 500,μ1= 10,μ2= 1000; (Z2)λ1= 10,μ1= 10,μ2= 1000; (Z3)λ1= 10,μ1=500,μ2=1000. In each BS,the CCU contains an actor network and a critic network. The actor network is composed of two layers of neural networks,namely a softmax layer and a full connection layer. Meanwhile,the critic network is composed of two full connection layers.
The local content popularity distribution pl(u) is modeled with a two-state Markov chain to simulate the dynamics of content popularity [6], as shown in Figure 6. The two states of local popularity proflies areand. That is, theFcontents in the caching system are allocated with different popularity probabilities descendingly in Markov stateforj ∈{1,2}.Meanwhile,the Zipf distribution is applied to simulate the request frequencies of different content in the content popularity characteristic. Given the parameter, thef-th content of the caching system in Markov stateis assigned with the popularity probability as
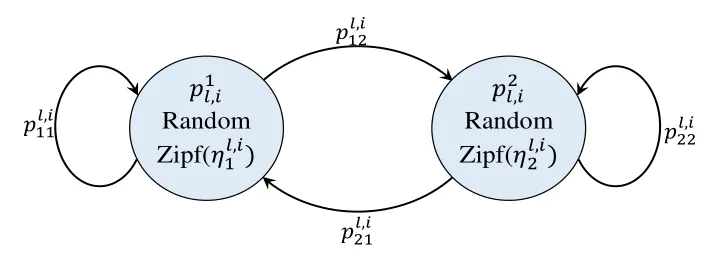
Figure 6. Local content popularity distributions.
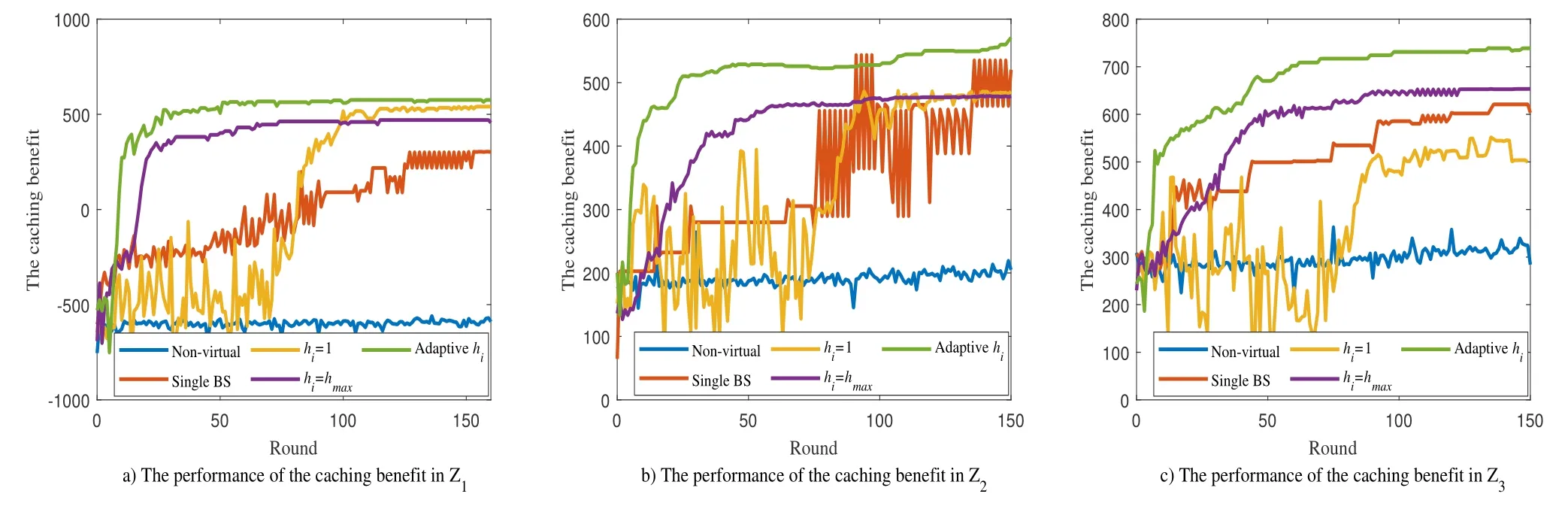
Figure 7. Comparison of the caching benefit under different schemes(M=2,F=10).
where0 controls the skewness of content popularities. A Zipf distribution with parameters, e.g.,= 1.5 is used to model the local content popularity distribution [19]. Formed by combining local content popularities,global content popularities are similar to local popularities.
Moreover, the Poisson flow process is applied to simulate the number of user request arrivals in a certain period. Assume that the arrival rate of BSiin the federation is. Hence, the probability of receivingNarequests for BSiin periodTais denoted as
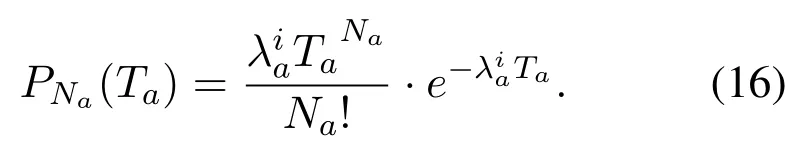
The arriving number of requests in a data acquisition interval[k] is generated based on the probability distribution. The BS counts the arriving user requests and acquires the local content popularity characteristics for the local virtual training.
To evaluate the caching performance of the proposed edge caching method, several simulations have been performed focused on the caching benefit and the cache hit ratio.The cache hit ratios in the edge caching system reflect the proportion of users’ requests satisfied by local BSs. For BSi, the cache hit ratio is denoted asrhit,i= ai(u)·pl,i(u), which can be calculated by the BS. We use the average of the cache hit ratios of BSs in the federation to represent the caching performance of the federation. Besides,some caching schemes are used as comparisons to the proposed caching method such as
? The FRL-based edge caching method with a fixed number of training times per roundhi=hmax.

Algorithm 1. The FRL-based algorithm with adaptive training times for edge caching.Require: The user request arrival rate λi, model parameter w, weight parameter α, max training times per round hmax and max training round K.Ensure: wfi 1: Initialize the caching state st ← s0, the round counter q ←0,and receiving tag t′i ←0.2: repeat 3: Get state st 4: q ←q+1 5: Estimate βi ← ∥?Fi(wli(t[k])) ??Fi(wg(t[k]))∥/∥wli(t[k]) ? wg(t[k])∥6: Estimate ?i ←∥Fi(wi(t[k]1))?Fi(wi(t[k]))∥7: Calculate hi[k]according to Eq.(14)8: R=images/BZ_76_428_1234_462_1279.png0 for terminal st V(st,wci) for non-terminal st 9: for l=0,1,2,...,(hi[k]?1)do 10: Perform virtual caching ation a(t[k]l)according to policy π(a|s;wai)11: Receive reward B(t[k]l)and new state st+1 12: R=B(t[k]l)+γR 13: Accumulate gradients w.r.t. wai: dwai ←dwa i +▽wai log π(ai|si;wai)A(si,ai)14: Accumulate gradients w.r.t. wci: dwci ←dwc i +?(Fci(wci))2/?wci 15: end for 16: Perform actual caching action a[k]according to policy π(a[k]|s[k];wai)17: Perform the update of wai using dwai and update of wc i using dwci 18: Send wli(t[k]hi[k])to the AN 19: Receive and store wg(t[k])from the AN 20: if q >1 then 21: Compare the loss functions of critic net Fi(wg(t[k]))and Fi(wli(t[k]))22: if Fi(wg(t[k]))≤Fi(wli(t[k]))then 23: wi(t[k])←wg(t[k])24: t′i ←t[k]25: else 26: wi(t[k])←wli(t[k])27: t′i ←t′i 28: end if 29: end if 30: until tr >K 31: wfi ←wi(t[k])
? The FRL-based edge caching method with a fixed number of training times per roundhi=1.
? The FRL-based edge caching method without virtual training(Non-virtual).
? The actor-critic learning-based edge caching method for a single BS without federation.
? The Least Recently Used (LRU) edge caching method[35].
Figure 7 depicts the comparison of the average caching benefit of BSs in the federation between the FRL-based edge caching method and the above comparison schemes under the parameter settings, i.e.,Z1,Z2andZ3. It is obvious that the proposed method obtains a higher convergence value with a faster convergence speed than other schemes in different scenarios. This finding verifies the effectiveness of the proposed federated process and the adaptive training times scheme in our FRL-based edge caching method. The proposed adaptive training times scheme improves the learning effect by seeking the tradeoff between the model fitting accuracy and data accuracy shown as Equation (14). Besides, the curves of the Non-virtual scheme and the proposed scheme show that the sandbox subsystem improves the availability of the caching model through proactive virtual training before making real caching decisions.
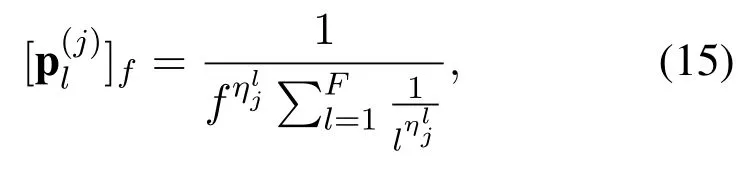
Moreover, the average cache hit ratio of BSs in the federation of the FRL-based caching method and the comparison schemes are shown in Figure 8. We can see that the proposed edge caching method outperforms other comparison schemes with a higher converged cache hit ratio and a more rapid convergence speed. Compared with the LRU method,the proposed scheme improves the cache hit ratio by 10%.

Figure 8. Comparison of the average cache hit ratio under different schemes(M=2,F=10).
To explore the performance of the proposed scheme in different environments,the caching benefit convergence value and convergence speed of the FRL-based method is evaluated with different local caching capacities, as shown in Figure 9. Thereinto, the RLbased method is the actor-critic learning-based edge caching method for a single BS without federation.The convergence speed is interpreted by the number of rounds required to reach the convergence value of the caching benefit. The smaller convergence round means the higher convergence speed. As shown in Figure 9, the FRL-based edge caching method outperforms the RL-based method for a single BS with a larger convergence value of the caching benefit and smaller convergence round.
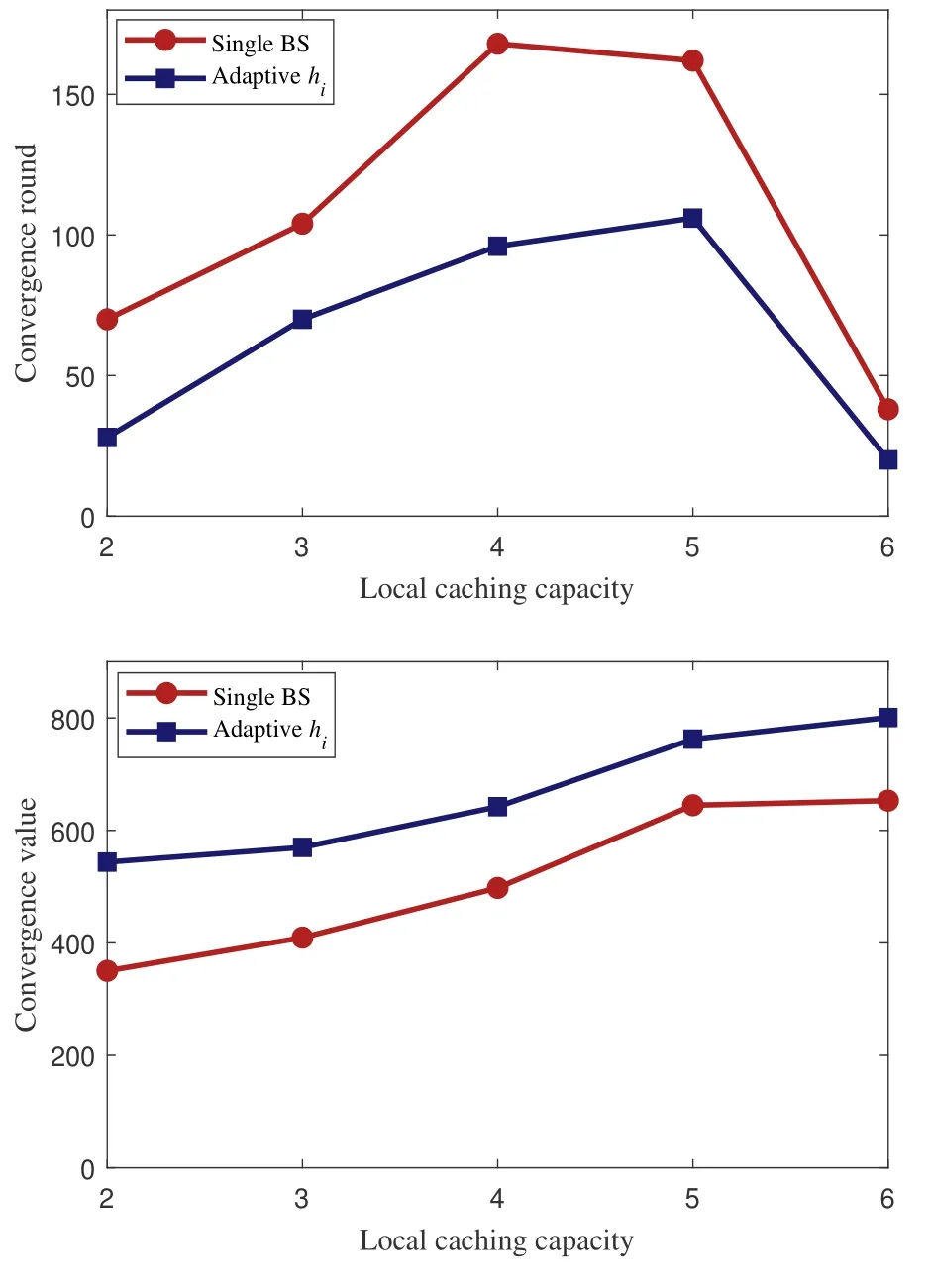
Figure 9. The convergence performance under different caching capacity.
In addition, with the increase in the local caching capacity,the converged benefit value increases gradually while the convergence speed becomes lower.Note that when the local caching capacityM=6,the number of rounds requires to reach the converged benefit value becomes lower.This is because the performance difference caused by different caching strategies is reduced when the cache capacity is large enough and most content requests can be satisfied locally. Especially,ifM=F,all the content in the edge system is cached locally,thus the convergence is reached at the beginning.
Considering the overall performance of the FRLbased caching method,we can conclude that the FRLbased edge caching scheme with adaptive training times shows its advantages in the edge caching control process, in terms of caching benefit, the hit ratio,and the convergence speed.
VI. CONCLUSION
In this paper, we have proposed the FRL-based algorithm with adaptive training times for multi-BS edge caching systems. Different from other federated learning-based methods,the proposed approach develops the parameter decision and training times calculation processes for purpose of mitigating the performance degradation brought by the non-i.i.d.characteristics of content popularity in BSs.Finally,the simulation results have verified that the proposed FRL-based method outperforms other baseline methods in terms of the caching benefit,the cache hit ratio and the convergence speed.
ACKNOWLEDGEMENT
This paper is supported by the National Key R&D Program of China(2020YFB1807800).
APPENDIX
A.Proof of Theorem 1
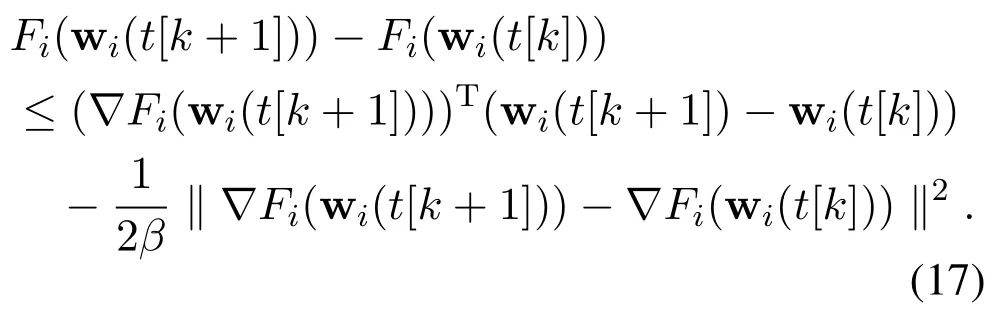
For BSithe local parameters update is performed by gradient descent method as wi(t+ 1) = wi(t)?η?Fi(wi(t)). Therefore, (wi(t[k+ 1])?wi(t[k]))can be rewritten as
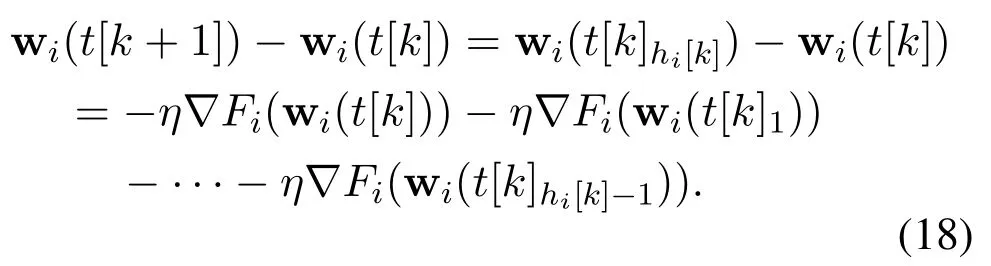
Thus,from Eq.(18)and gradient descent method,we get
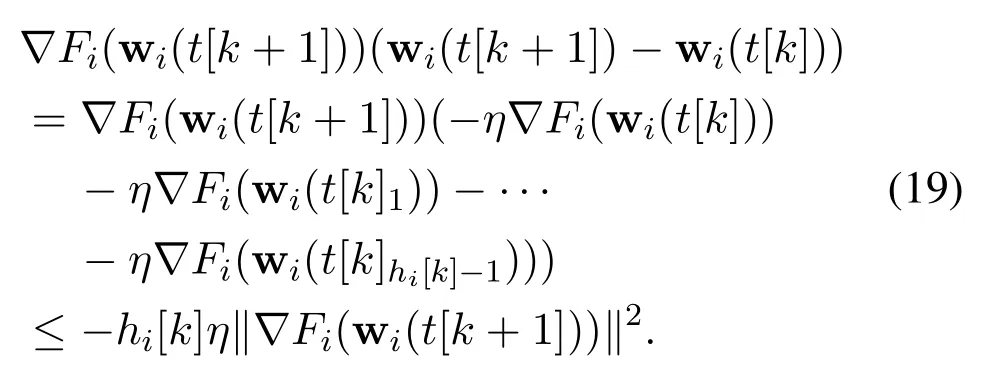
By substituting Eq.(19)back into Eq.(17),we have
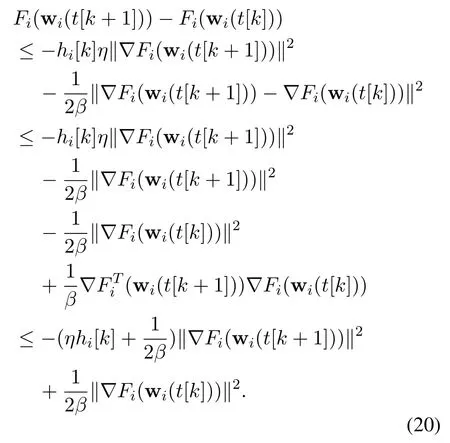
The convex condition gives
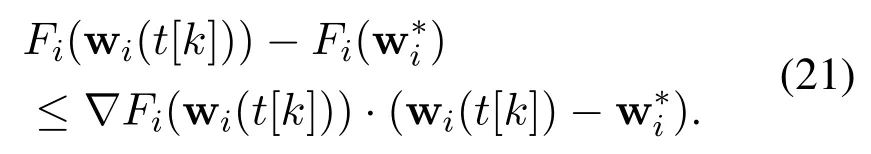
Through the Cauchy-Schwarz inequality, Equation(21)can be rewritten as
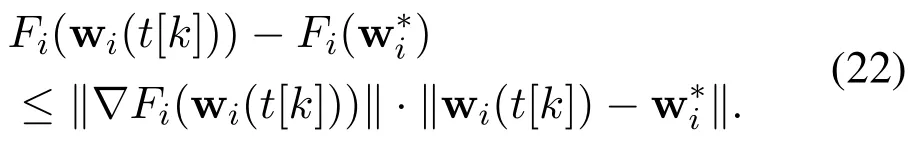
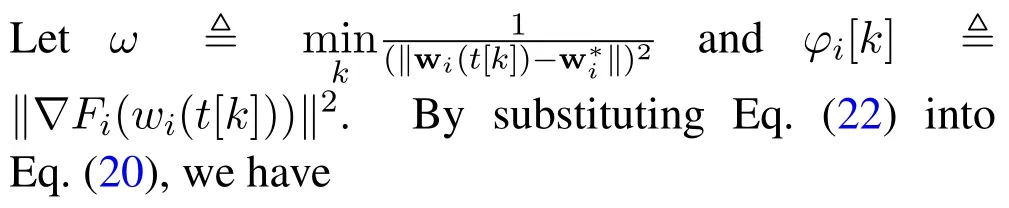
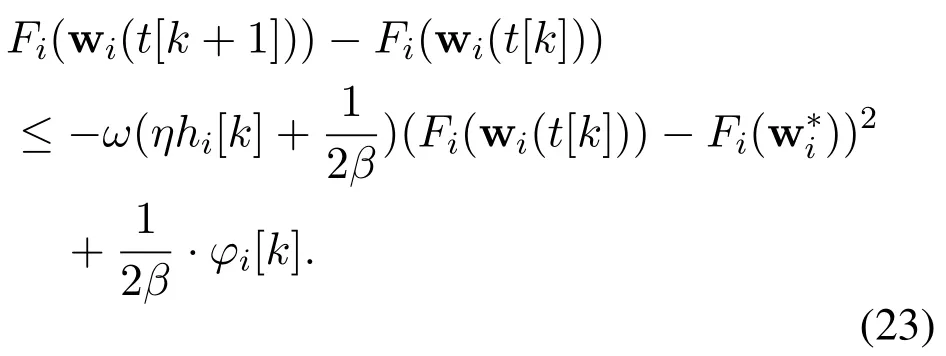
It is assumed that?satisfiesFi(wi(t[k]))?Fi(wi(t[k+1]))≥? >0 for allk. Consequently,Eq.(23)can be rewritten as
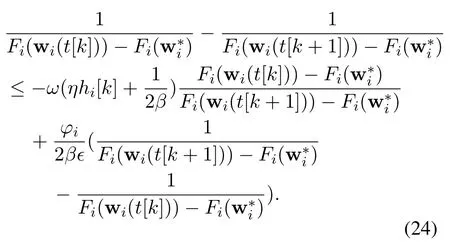
The gradient descent method gives
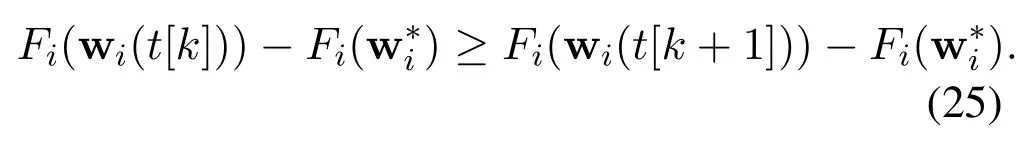
Hence,
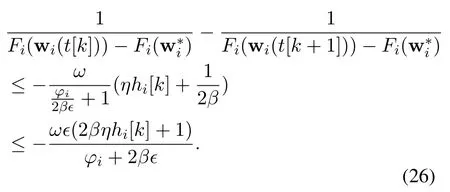
Accumulating the inequality Eq.(26)from round 1 to roundk,we get
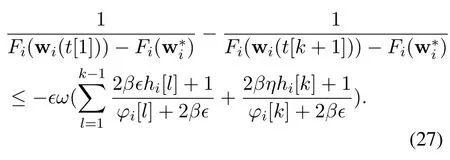
Since the condition 0< θi[k]≤ Fi(wi(t[k]))?Fi()is satisfied for allk,Eq.(27)yields
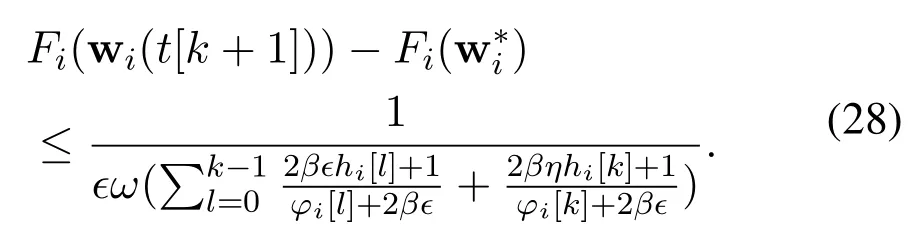
- China Communications的其它文章
- Edge Intelligence for 6G Networks
- Register Allocation Compilation Technique for ASIP in 5G Micro Base Stations
- Deep Reinforcement Learning Based Joint Partial Computation Offloading and Resource Allocation in Mobility-Aware MEC System
- Joint Computing and Communication Resource Allocation for Edge Computing towards Huge LEO Networks
- Paving the Way for Economically Accepted and Technically Pronounced Smart Radio Environment
- Arbitrary Scale Super Resolution Network for Satellite Imagery

