Joint Computing and Communication Resource Allocation for Edge Computing towards Huge LEO Networks
Min Jia,Liang Zhang,Jian Wu,Qing Guo,Xuemai Gu
Communication Research Center,School of Electronics and Information Engineering,Harbin Institute of Technology,Harbin 150080,China
Abstract: The satellite-terrestrial cooperative network is considered an emerging network architecture,which can adapt to various services and applications in the future communication network. In recent years,the combination of satellite communication and Mobile Edge Computing(MEC)has become an emerging research hotspot. Satellite edge computing can provide users with full coverage on-orbit computing services by deploying MEC servers on satellites. This paper studies the task offloading of multi-user and multi-edge computing satellites and proposes a novel algorithm that joint task offloading and communication computing resource optimization (JTO-CCRO).The JTO-CCRO is decoupled into task offloading and resource allocation sub-problems. After the mutual iteration of the two sub-problems, the system utility function can be further reduced. For the task offloading sub-problem,it is first confirmed that the offloading problem is a game problem. The offloading strategy can be obtained from the Nash equilibrium solution. We confirm resource optimization sub-problem is a convex optimization problem that can be solved by the Lagrange multiplier method. Simulation shows that the JTO-CCRO algorithm can converge quickly and effectively reduce the system utility function.
Keywords:satellite edge computing; task offloading;resource allocation;potential game;nash equilibrium
I. INTRODUCTION
The terrestrial communication network has transformed from 1G to 5G. However, the current terrestrial communication network cannot achieve full-area coverage around the world.On one hand,due to the influence of terrain factors such as deployment costs,the ground communication network cannot provide communication services for users in harsh environments because there is no base station deployment. On the other hand, the terrestrial communication network is easily affected by natural disasters, and the terrestrial communication network has a weak ability to resist natural disasters. The future development trend of 6G is to provide users around the world with full coverage in the true sense[1].Due to its coverage and strong resistance to natural disasters, the satellite network can be used as a powerful supplement and can achieve true seamless coverage in the whole area. The LEO satellite has a low orbital altitude and low transmission delay,which has become a research hotspot.
With the development of science and technology,more and more computing-intensive applications are required, such as AR, VR, and other applications requiring more computing resources. Generally speaking,the limited computing power on the device cannot meet the QoE requirements of computing-intensive applications. To solve this, the concept of cloud computing is proposed that users could offload their computing-intensive tasks to the cloud center. If too many users offload computing tasks to the cloud center, which will cause problems such as transmissionblocking and information leakage. MEC [2, 3] is a product that conforms to this development trend. By sinking the caching function and computing function in the cloud computing to the edge of the network,MEC enables users to satisfy the computing and transmission needs to a large extent at the network edge,making up for the lack of user computing power and the limited energy supply. The defects of high service delay and user energy consumption brought about by limitations and long-distance transmission of large amounts of data have improved.Compared with cloud computing, MEC makes user business processing no longer need to upload to the cloud center through multi-hop routing. The transmission distance of the link is short, which can better meet the user QoE.Literature [4] proposes computational offloading for constraint-based multi-objective optimization to minimizing the cost function. The authors design an evolutionary algorithm that makes a trade-off between energy and task delay to find the best sample. The application of game theory to wireless networks is proposed in[5],mainly introducing the application of game theory in MEC, focusing on the main challenges that MEC services impose on wireless resources. Includes model evaluation and how to optimize various tradeoffs in resource-constrained MEC scenarios. An EUA game problem is proposed in [6] for computing offloading.The authors prove that the EUA is a potential problem and exists Nash equilibrium solution.A novel decentralized algorithm is proposed to solve the EUA problem. Literature[7]studies computational offloading in a multi-carrier MEC system. Users are regarded as players and subcarriers as alliances for computational offloading. The Nash equilibrium solution is formulated with low algorithm complexity. Literature[8] proposes a low-complexity computation offloading strategy based on deep reinforcement learning to minimize user energy consumption. However,the impact of resource allocation on system utility functions is not considered. Literature[9]proposes a multi-user multi-server partial offloading strategy. Jointly optimize the user’s computing speed, transmission power and offload rate to minimize the user’s delay and energy consumption.
In recent years, some researchers have proposed combining LEO satellites and mobile edge computing to provide users with low-latency computing offloading services by deploying MEC servers on LEO satellites.The reference[10–12]mainly introduces the possible deployment methods and challenges of deploying MEC servers on LEO satellites. A three-layer offload architecture of the terrestrial cloud center and LEO computing platform to provide heterogeneous computing resources for terrestrial users is proposed in[13]. A low-complexity algorithm is proposed to minimize system energy consumption to obtain offloading decisions. Literature[14]proposes a novel architecture for LEO edge computing satellites, which decomposes the original problem into the minimization of the space part and ground part. The authors point out that there exist specific offloading bits that can minimize the system utility. An edge-cloud collaborative air-space-ground-assisted edge computing algorithm is proposed in [15], in which UAVs deployed MEC servers. Users can choose offload to UAVs for edge computing or access the terrestrial cloud data center through satellites. The authors propose a task offloading strategy based on deep reinforcement learning and an optimized resource allocation algorithm to minimize system cost. The authors in literature [16]believe that the request scheduling and service placement of different services are deeply coupled in terms of resource utilization. The optimization method for joint request scheduling and service placement under LEO edge computing satellites is proposed. Compared with the baseline model, the algorithm complexity is further reduced. Literature [17] proposes a multi-user single-server scenario where LEO satellites deploy MEC servers and proposes a joint computing offloading and resource allocation strategy based on game theory that minimizes user energy consumption within the coverage area. A game-based offloading framework under multi-user and multi-server is proposed in [18]. Based on the queuing theory to minimize the system utility and an iterative low complexity algorithm is proposed.
Inspired by the above reference, This paper proposes a multi-user and multi-server task offloading and resource optimization algorithm under the LEO edge computing satellite. Since the offloading variable is discrete and the resource variable is continuous, the problem is a mixed-integer nonlinear problem. In this paper,a joint task offloading and communication computing resource optimization (JTO-CCRO) algorithm is proposed,which considers the uplink bandwidth and computing resource allocation strategy, and the task offloading strategy. To reduce the complexity,we de-couple the JTO-CCRO into two sub-problems. One is computing offloading under the premise of optimal resource allocation. We have proved computing offloading problem is an exact potential game problem with a Nash equilibrium solution. Another is optimal bandwidth resources and computing resources allocation under the offloading strategy. The resources allocation problem is convex that can be solved by the Lagrange multipliers method. Experimental simulations show that the JTO-CCRO algorithm can effectively reduce the system utility function.
The main contributions are as follows:
(1) This paper studies the optimization strategy of computing offloading for multi-user and multi-edge computing satellites and propose a JTO-CCRO algorithm. By jointly optimizing the offloading strategy,the bandwidth,and computing resources of LEO satellites to minimize the system utility function.
(2) A game-based task offloading and resource optimization scheme which decouples the original problem into two subproblems is proposed. The task offloading subproblem is proved to be an exact potential game and exists Nash equilibrium solution. For the resource optimization subproblem, the optimal bandwidth and computing resources can be solved by the Lagrange multiplier method.
(3) According to the simulation experiments, the JTO-CCRO algorithm proposed in this paper converges quickly and can effectively reduce the system utility function.
The rest of this paper is organized as follows. Section II introduces the JTO-CCRO system model,communication model, computing model and problem formulation. Section III introduces task offloading model, resource allocation model and JTO-CCRO algorithm. In Section IV,the simulation results are presented. Finally,Section V conclude this paper.
II. SYSTEM MODEL
In this section, LEO satellites deployed MEC servers provide computing services to users within the coverage area to minimize the system utility function. The JTO-CCRO algorithm simulation scene is shown in Figure 1. In this scenario, users can offload tasks to LEO edge computing satellites or cloud centers through the GEO relay. In this paper, we just consider offloading tasks to LEO edge computing satellites. Consider the usersD={i:i= 1,2,...,k},wherekis the number of users. The edge computing satelliteM={s:s= 0,1,2,...,n},wherenis the number of edge computing satellites. Whens= 0,it means that user tasks are executed locally. Generally speaking,the capabilities of satellites are limited,and performing too many computing tasks on one satellite has a large impact on the battery and task completion time will be long. Therefore, this paper assumes that the processing capacity of each satellite is.That is to say,satellitescan execute concurrentlycomputing tasks at most.
Suppose each user has a computing task, denote as, wheredirepresents the data size,cirepresents the number of computing cycles required to complete the task, andrepresents the maximum tolerable delay. Computing tasks can compute locally or offload to edge computing satellites. For the sake of convenience, this paper adopts the Frequency Division Multiple Access (FDMA) to mitigate interference. Each satellite provides computing services to users in different frequency bands without considering inter-satellite interference. The notations mainly used are summarized in Table 1.

Table 1. Mainly notations.
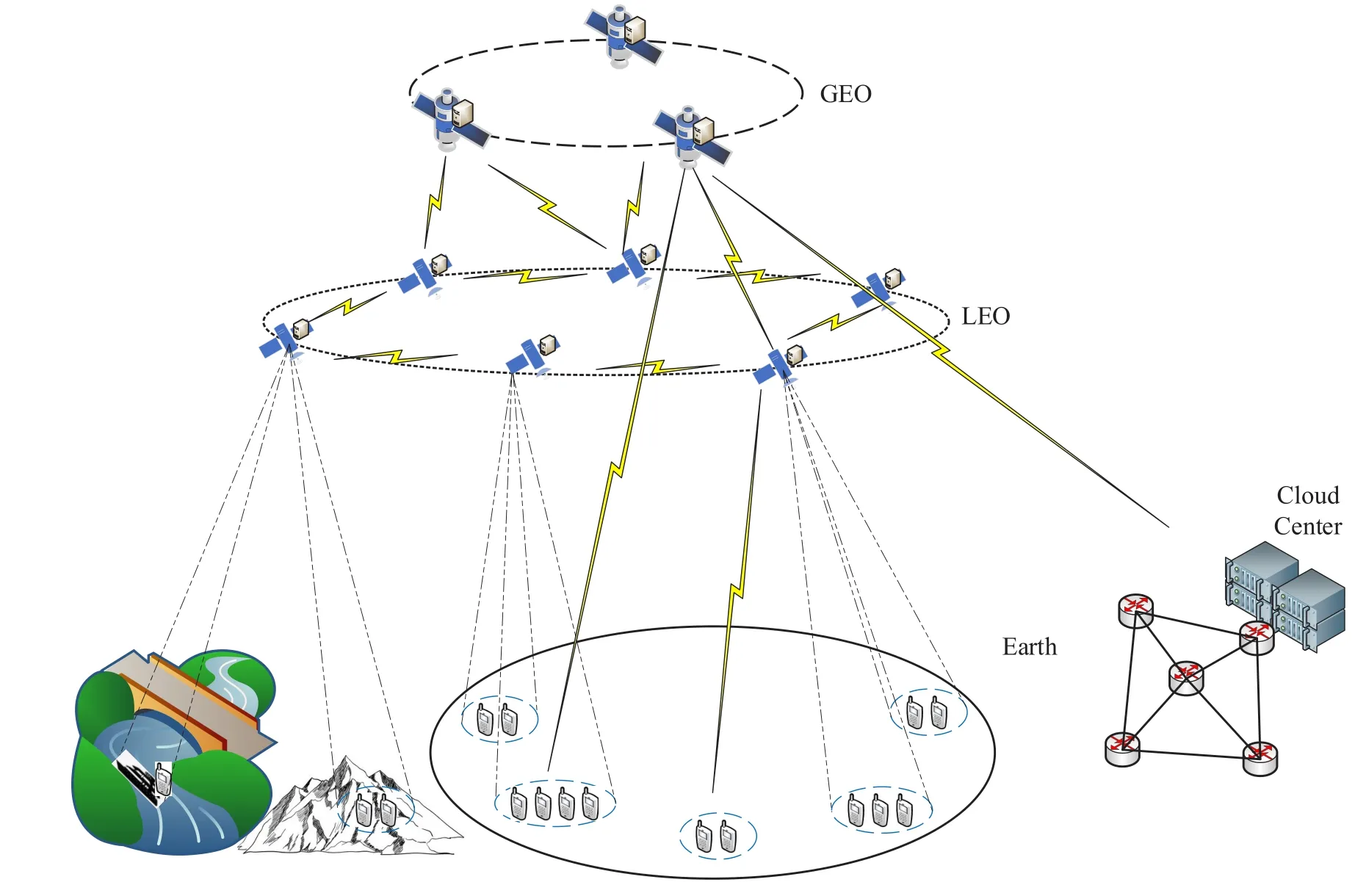
Figure 1. System model of satellite edge computing towards multi-server multi-user.
2.1 Communication Model
When the terrestrial user has a computing request,the user will choose local computing or offload computing tasks to edge computing satellites to satisfy their QoE.Once the user has an offload request and offloads computationally intensive tasks to the LEO satellite.Generally speaking,the computing result is relatively small compared to the original data. Therefore, the time of the result back can be ignored. The uplink data rate between useriand satellitesis:
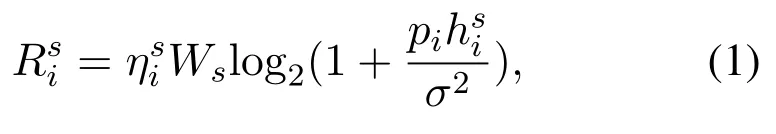
whereis the percentage of Bandwidth resource allocation,Wsis the bandwidth of satellites,pithe transmit power of useri,is the channel gain,σ2is the background noise power.
Different from terrestrial communication,the satellite channels loss mainly consists of free space loss,atmospheric loss, polarization loss, and antenna misalignment loss. Atmospheric loss is due to absorption and scattering by atmospheric particulate matter.Polarization loss occurs when the receiver does not match the polarization of the incident electromagnetic field, while antenna misalignment loss is caused by the misalignment of the transmit and receive antennas. Since atmospheric loss are predictable and polarization loss, as well as antenna misalignment loss,are usually small. Therefore, for the convenience of analysis,this paper only considers the free space loss,denoted as, whereλwavis the wavelength andHnis the distance.
2.2 Computational Model
For the computing model,we assume userihas a computing taskTi.The task can be calculated locally or offload to edge computing satellite to meet the user QoE requirements. For a given taskTi,its offloading strategy can be expressed0,1},?i ∈D,s ∈Mwhere

(1)Local Execution
When userichooses local execution,the task delay depends mainly on the computing power of the device.Given the computing frequencyof the device, the local execution time of useriis:
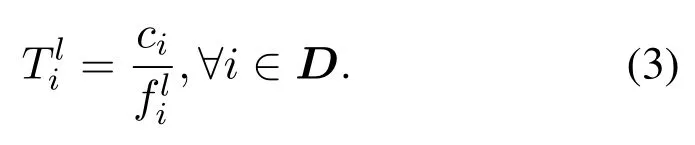
Once given the computing frequency,the local computing energy consumption can be written:
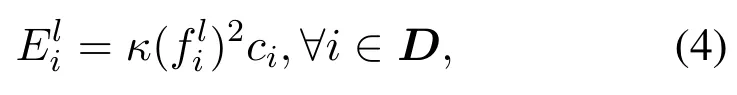
whereκis the chip coefficient, which depends mainly on the manufacturer. Based on local execution time and execution energy consumption,the local computation utility function can be expressed as:
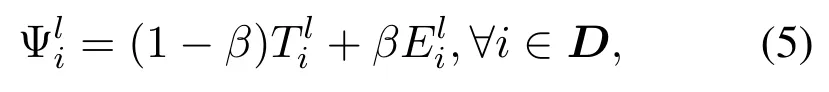
whereβis the weight factor of energy consumption and delay.
(2)LEO Offloading Computing
When userioffloads computing tasks to the edge computing satellites. Due to the large physical distance, the task offloading delay to the LEO satellite includes the task transmission delay, propagation delay,and edge computing satellite task execution delay.The offloading time for userioffload to satellitesis:
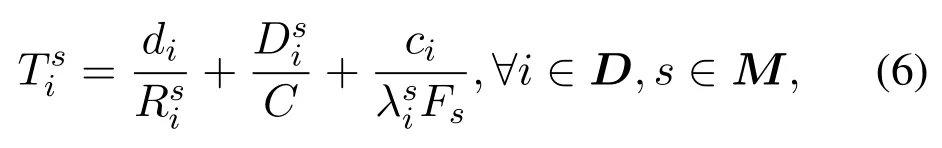
whererepresents the distance between useriand satellites,Cis the light speed, andFsrepresents the calculation frequency of LEO satellites.
For the offloading energy consumption,we only focus on user offloading energy consumption. The offloading energy consumption in user is the transmission energy consumption,which can be expressed as:
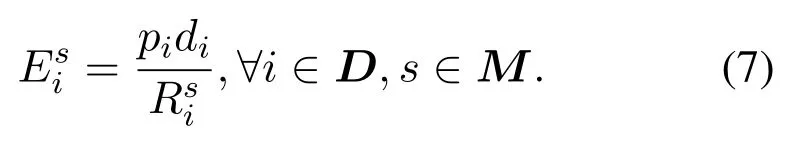
Based on the offloading delay and energy consumption, the task offloading utility function can be expressed as:
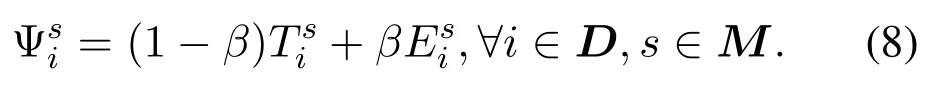
Based on the utility function of local computing and task offloading,we can get the utility function of taski,which can be expressed as:
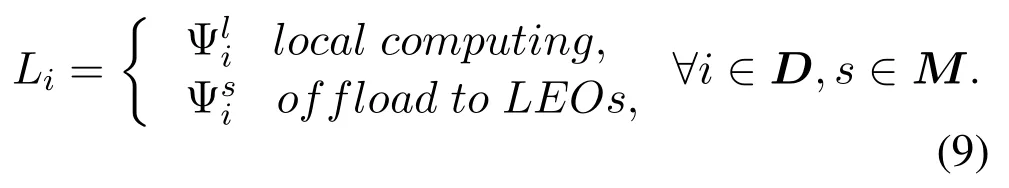
2.3 Problem Formulation
For local computing, the task completion time does not include data transmission and propagation delay.However, there will be a long execution delay due to limited computing power. When computing tasks offload to the edge computing satellite which produce an additional transmission and propagation delay. The execution time can reduce with the help of the edge computing server. Therefore, it is vital to perform reasonable scheduling optimization of tasks to meet different QoE. The system utility function can be expressed as:
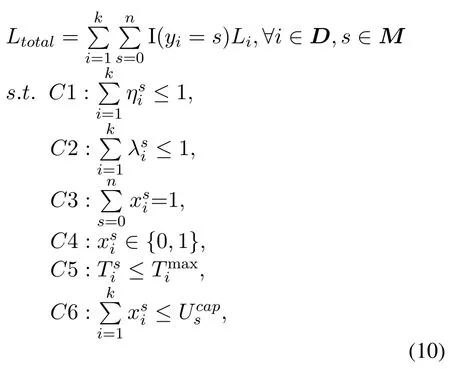
where I(yi=s))=1,if and only ifyi=s,that is to say= 1. C1 indicates the constraint of bandwidth resources for LEOs. C2 is the constraint of computing resources for LEOs. C3 indicates that task is either executed locally or offloaded. C4 indicates that the offload variable is a binary integer. C5 is the constraint of task maximum available tolerable time. C6 indicates that the number of tasks offloaded to LEOs cannot exceed their capacity.
III. JOINT OPTIMIZATION TASK OFFLOADING AND RESOURCE OPTIMIZATION
Since the offload variable is a binary integer variable,the bandwidth and computing resources are continuous variables, the system utility function is a nonlinear mixed integers optimization problem. The JTOCCRO algorithm proposed in this paper decouples the original problem into two sub-problems. For computational offloading problem under optimal bandwidth and computing resources allocation, we first prove the task offloading subproblem is an exact potential game problem. The offloading strategy can be obtained through game theory. While for resource allocation sub-problem, once the offloading strategy is fixed,the optimal bandwidth and computing resources allocation can be solved by the Lagrange multiplier method.
3.1 Offloading Game Establishment
Defineyi ∈{0,1,...,n}is the offloading policy for taski. Among them,yi=0 indicates that the task is executed locally,yi=s,indicates that taskioffloads to the edge computing satellites, and definesy?idenotes the offloading strategy of other tasks except for taski. The utility function for taskican be defined as:
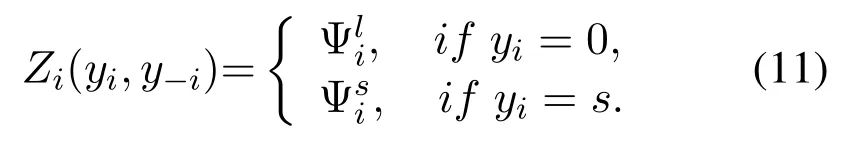
In this part,we analyze the optimal offloading strategy through game theory. In this game, the players are the user tasks and these tasks compete for communication and computing resources in the system to minimize the system utility function.
Definition 1.In the first, define game G={D,(yi){i∈D},(Zi(yi,y?i)){i∈D}} , where D represents all user tasks,(yi){i∈D} represents a set of offloading strategies,(Zi(yi,y?i)){i∈D} represents thesystem utility function. In game, each player aims to minimize its utility function, which can be expressed as:
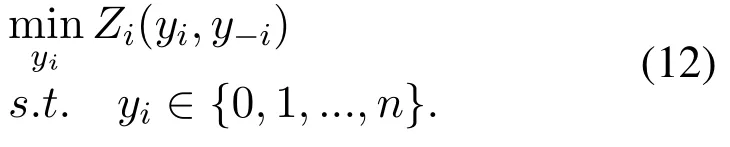
Definition 2.There is a set of offloading decisions that make the system reach the Nash equilibrium solution. Due to the self-stability of theNash equilibrium solution, there is no game player to break the balance, and all game players will converge to the Nash equilibrium solution, which can be expressed as:
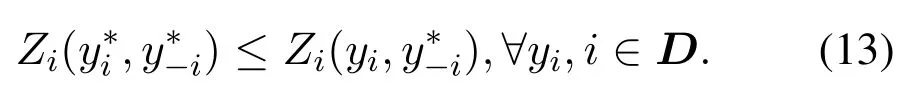
The purpose of game is to minimize the utility function of each player, that is, the change of each player strategy must be monotonic. Assuming that the utility function of each player can map to a potential function, then the potential function is also monotonic,such games are called potential games. To prove that there exists a Nash equilibrium solution, we need to prove thatGis an exact potential game by introducing a potential function Φ(y).
Definition 3.In the game, if there exists a functionΦ(y): y →R that satisfies the following relationship for all game players, the game is an exact potential game.

We first define the potential function as follows.
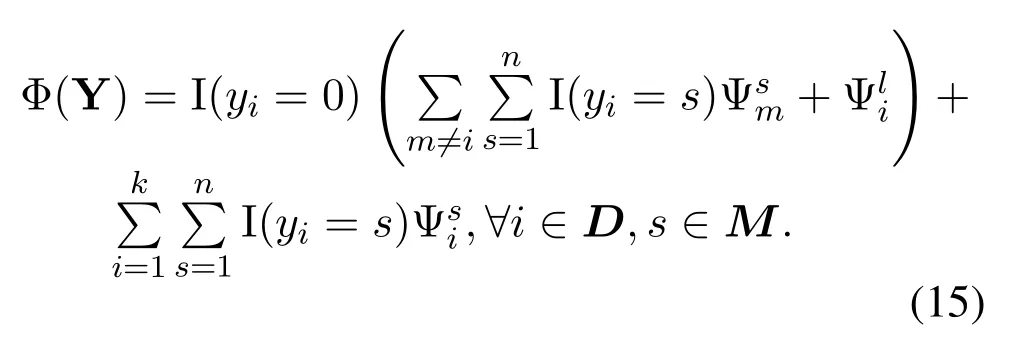
Theorem 1.G is an exact potential game under the potential functionΦ(y)defined in Eq.(15)(see APPENDIX A).
3.2 Resource Allocation
Local computing only involves task scheduling and does not involve resource allocation. After obtaining the offloading strategy from the game theory, Eq.(10)can be rewritten as:
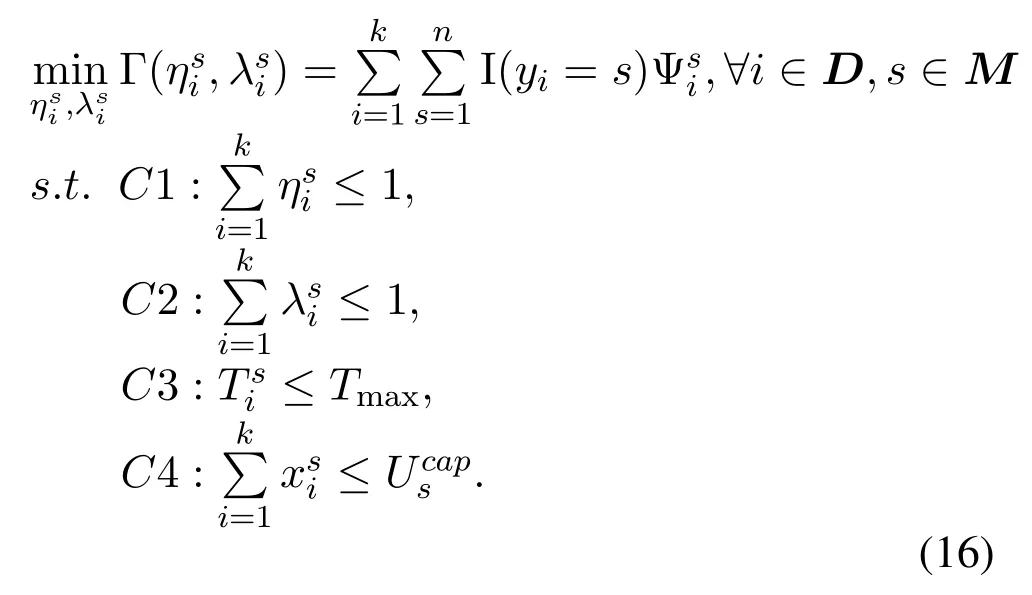
When taskioffloads to satellites, Eq.(16) can be rewritten as:
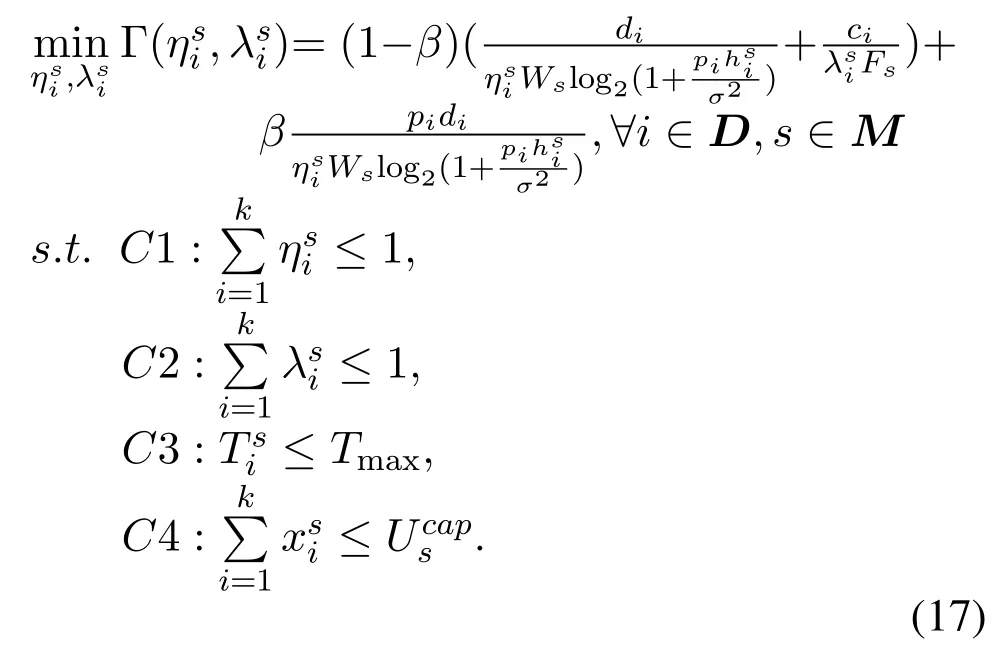
The constraint of the Eq.(17)is convex and the Hessian matrix can be expressed as:
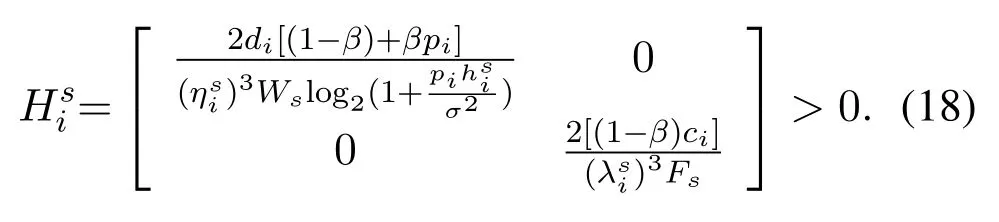
It can be seen from Eq.(18)that the Hessian matrix is positive definite. The problem Eq.(17) is a convex function that can be solved by lemma 1.
Lemma 1.The optimal bandwidth and computing resource optimization for the resource problem Eq.(17)can be expressed as(see APPENDIX B):
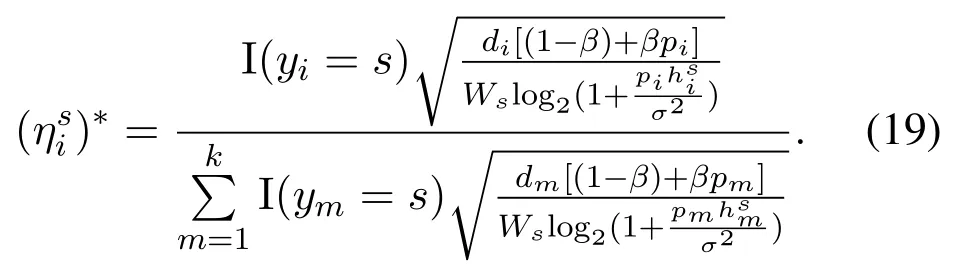

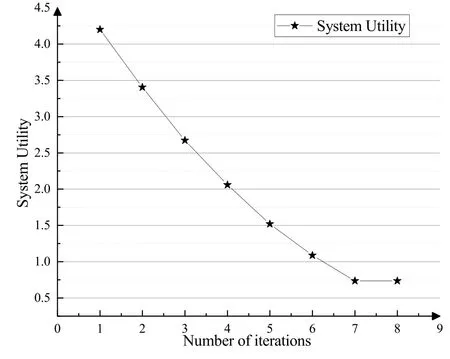
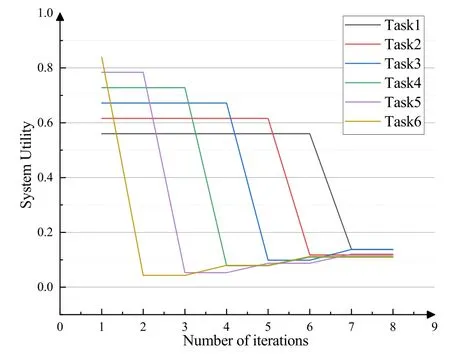
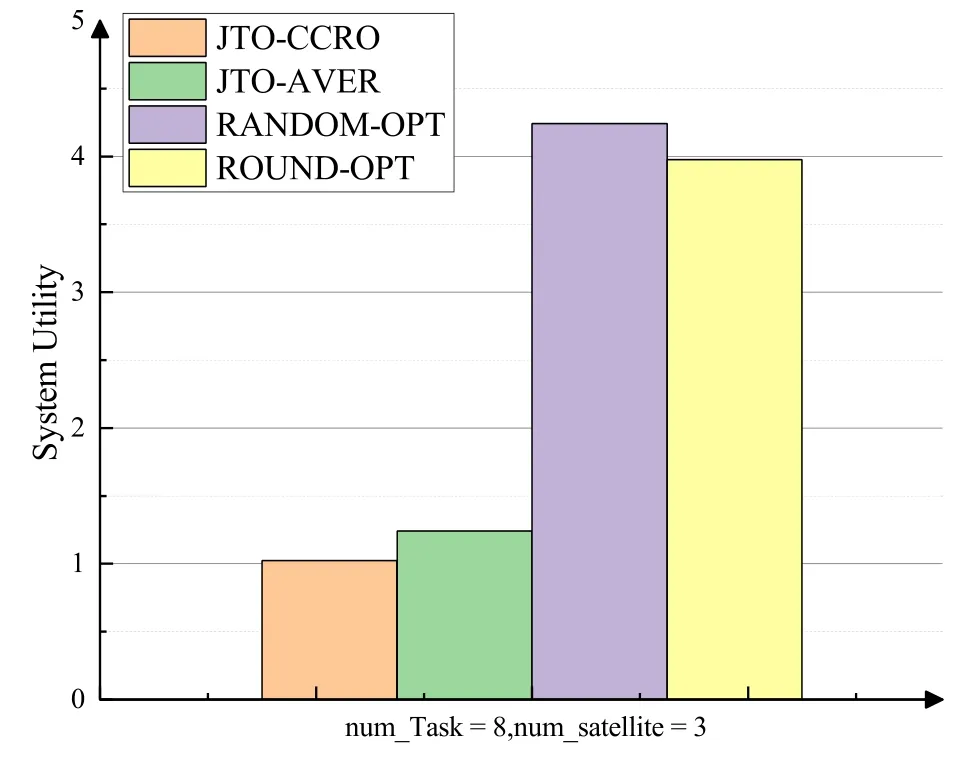
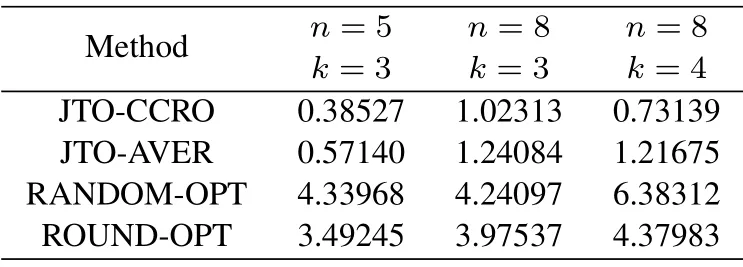
Algorithm 1. JTO-CCRO algorithm.Require: D,M,pi,σ2,Ws,Dsi,Ucaps ,di,ci,fli,Fs hsi,Tmax i ,C,κ Ensure: (ηsi)?,(λsi)?,y?1: initialization yi=0,?i ∈D 2: t=1 3: while t Definition 4.When the offloading strategy of task i changes from yi to ,if the following conditions are The JTO-CCRO algorithm proposed in this paper with low complexity. We decouple the original problem into task offloading and resource allocation subproblems. Through mutual iteration of these two subproblems reduce the system utility function. The specific algorithm description is shown in Algorithm 1.All users initialize local computation at first(Line 1).At each time slot t,we first record the offloading strategy,bandwidth,and computing resource allocation results of the current time slot(Line 4-6). Next,traverse all users,and get the user’s better strategies according to Definition 4. Random select an offloading server from the set of better strategies reduces the system utility function. According to the current offloading decision and Eq.(19)and Eq.(20),we can get the bandwidth and computing resource allocation results, and the current time slot iteration is completed(Line 7-15).In each subsequent time slot, all users update the offloading decision,bandwidth,and computing resource allocation results until the better strategies are empty(Line 16-18). Finally, according to the last computing time slot,the final computing offloading decision,bandwidth, and computing allocation results are obtained(Line 19-20). To verify the JTO-CCRO algorithm,we conduct many experiments on a machine configured with Intel Core i7-10700K CPU @3.8G, 32G RAM. Users distribute randomly in an area of 2Km×2Km and the satellite orbital altitude is 500Km. It is assumed that the computing power of the device is 1GHz. The computing power of the satelliteFsis randomly selected from[20,25] GHz. The MEC server capacityis randomly selected from[1,5], and communication bandwidth follows a Gaussian distribution with meanμi=20MHz andσi=0.15μi. The data size of the taskdiis randomly selected from [0.5,3] Mbits, the required CPU cyclesciis randomly selected from [400,1000]Megacycles, and the maximum tolerable delayis randomly selected from [0.1-2] sec. The transmit powerpiis randomly selected from[0.01-0.2]W.The chip coefficientκis set to 1.2e-28 andβto 0.5. The Monte Carlo simulation is repeated 10,000 times for each scenario and average the results. We compare the system utility performance against the following baselines. 1. JTO-CCRO:The offloading strategy is solved by game theory in this paper and the resource allocation scheme adopts the optimal resource allocation strategy. 2. JTO-AVER:The offloading strategy is obtained by the game theory and the average resources allocation method used. 3. RANDOM-OPT:The offloading strategy is random offloading and the resource allocation adopts the optimal resource allocation strategy. 4. ROUND-OPT:The offloading strategy adopts the polling method that provides services in turn and the resource allocation adopts the optimal resource allocation strategy. To verify the feasibility of the JTO-CCRO algorithm, we first setk= 6 andn= 2. The simulation results are shown in Figure 2 and Figure 3. From Figure 2, we can see that the JTO-CCRO algorithm proposed in this paper can converge quickly. After several iterations,the algorithm converges to the Nash equilibrium point. All tasks will eventually reach a consistent equilibrium state,as seen from Figure 3,after several iterations, the utility function of the task will converge. Our optimization goal is to minimize the system utility function. For some tasks, such as task 6,due to competing wireless computing resources between tasks, the utility function of the task will increase,but the system utility function will decrease. Figure 2. JTO-CCRO algorithm covergence diagram. To verify the effectiveness and universality of the JTO-CCRO, we set the new simulation scenario ask= 8 andn= 3. The JTO-CCRO algorithm proposed in this paper compares with JTO-AVER,RANDOM-OPT, and ROUND-OPT, the results are shown in Figure 4. The JTO-CCRO algorithm jointly considers the impact of computing offloading and resource optimization on system performance. From Figure 4 we can see that the JTO-CCRO algorithm is the best, followed by the JTO-AVER. Once users adopt the ROUND-OPT method, it does either consider the communication and computing resource of the MEC server or the channel condition between users and satellites, so the performance is poor. But ROUND-OPT is better than RANDOM-OPT because of uncertainty. Figure 3. Task utility function changes in the JTO-CCRO. Figure 4. Comparison of different algorithms. We conduct several different simulation scenarios to verify the JTO-CCRO algorithm, the experimental results are shown in Table 2. From Table 2, it can be seen that when the satellite edge server is 3,the system utility function increases with the number of users, mainly because users compete for limitedcommunication and computing resources. When the number of users is 8,with the increase of the satellite MEC servers, the system utility function reduces as the system computing and communication capabilities increases. The performance of JTO-AVER is lower than JTO-CCRO because of an average resource allocation method used, but better than RANDOM-OPT and ROUND-OPT. Since RANDOM-OPT adopts a random offloading strategy,the system utility function fluctuates greatly.Due to the limited computing power of the MEC server, once the ROUND-OPT method used,users may not be able to access the satellite,thus users can only choose local computing resulting in an increase in the system utility function. Table 2. Different algorithms comparison in different scenarios. Figure 5. The relationship between tasks and system utility function. We further verify the relationship between tasks and the system utility function.In our simulation,the number of tasks increases from 3 to 18, these tasks are competing for wireless resources in the system. From Figure 5 we can see, the system utility function increases with the increase of tasks. In the initial stage,the user will choose the MEC server with good channel conditions and strong computing power to complete the task offloading, so the increase rate in the initial stage is moderate. As the number of tasks increases, users will gradually occupy the entire system capacity and the rate of system utility function increases. When the users exceed the system capacity, the excess users can only execute locally, so the growth rate of system functions is faster. The MEC server deployed on the LEO satellite proposed in this paper provides computing offloading services for users. The JTO-CCRO algorithm proposed aims to minimize the system utility function under the premise of satisfying user QoE.Since the offload variables are binary integers,and the bandwidth and computational allocation factor are continuous variables,the problem is a mixed-integer nonlinear problem. We decouple the original JTO-CCRO algorithm into two sub-functions,task offloading and resource allocation.Firstly, it proves that the task offloading problem is an exact potential game and there exists a Nash equilibrium. Secondly, it verifies that the resource allocation sub-problem is a convex problem that can be calculated by the Lagrange multiplier method. These two sub-problems iteratively reduce the system utility function. It can be obtained from the experimental results the JTO-CCRO algorithm can quickly converge.Compared with other baseline models,the JTO-CCRO algorithm can effectively reduce the task completion time and user energy consumption. ACKNOWLEDGEMENT This work was supported by the National Key Research and Development Program of China under Grant 2021YFB2900500,the Natural Science Foundation for Outstanding Young Scholars of Heilongjiang Province under Grant YQ2020F001, and the Fundamental Research Funds for the Central Universities under Grant FRFCU 9803503821. APPENDIX A Proof.If all conditions in Eq.(15) are satisfied,Gis an exact potential game. Case 1.If the offloading decision of task i changes from local calculation to satellite j, according to Eq.(15),we can get: Case 2.if the offloading decision of task i changes from satellite j to local computing, according to Eq.(15),we can get: Case 3.if the offloading decision of task i changes from satellite j to satellite h,according to Eq.(15),we can get: After the verification of the above three situations,Gis an exact potential game. There exists a Nash equilibrium solution. APPENDIX B Proof.Proof for Lemma 1. The Lagrange function of Eq.(17)can be expressed as: whereμ,ρa(bǔ)re Lagrange multipliers. Take the firstorder partial derivatives for the bandwidth factor and the computing resource coefficient,we can get: According to the properties of the Lagrange multiplier method, it can be obtained by setting its firstorder partial derivative equal to zero. The optimal bandwidth resources and computing resources are obtained respectively. Since the Lagrange multipliers are all greater than zero,according to the KKT condition,we can get: Taking Eq.(28) and Eq.(29) into KKT conditions Eq.(30)and Eq.(31),we can get: Substitute the results of Eq.(32) and Eq.(33) into Eq.(28) and Eq.(29) to obtain the optimal bandwidth and computing resources allocation: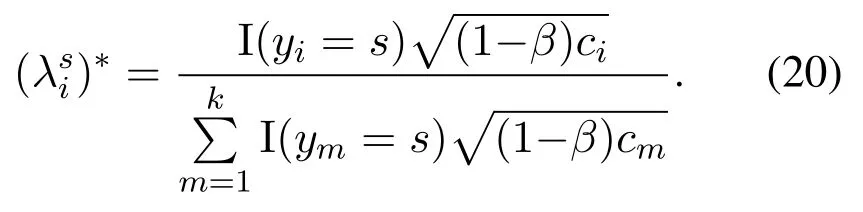
3.3 Joint Task Offloading and Communication Computing Resource Optimization
IV. SIMULATION
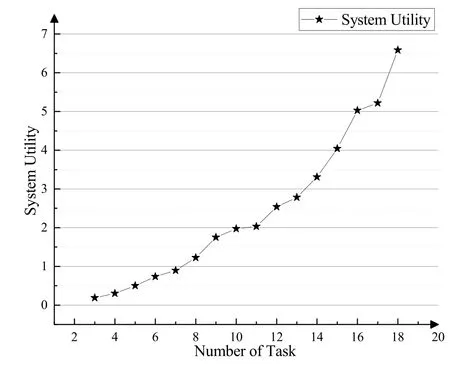
V. CONCLUSION
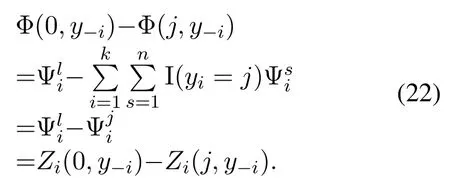
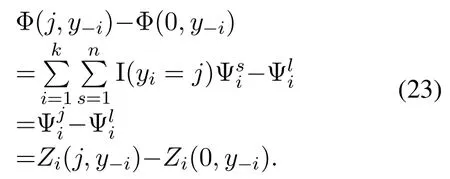
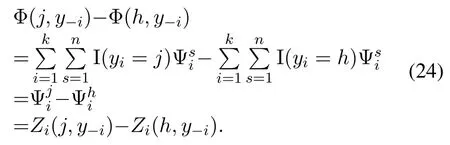
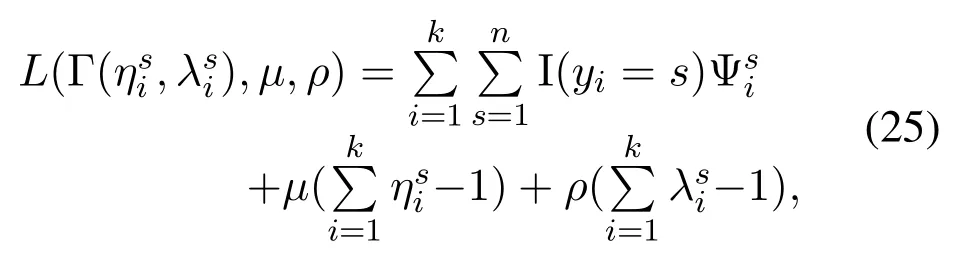
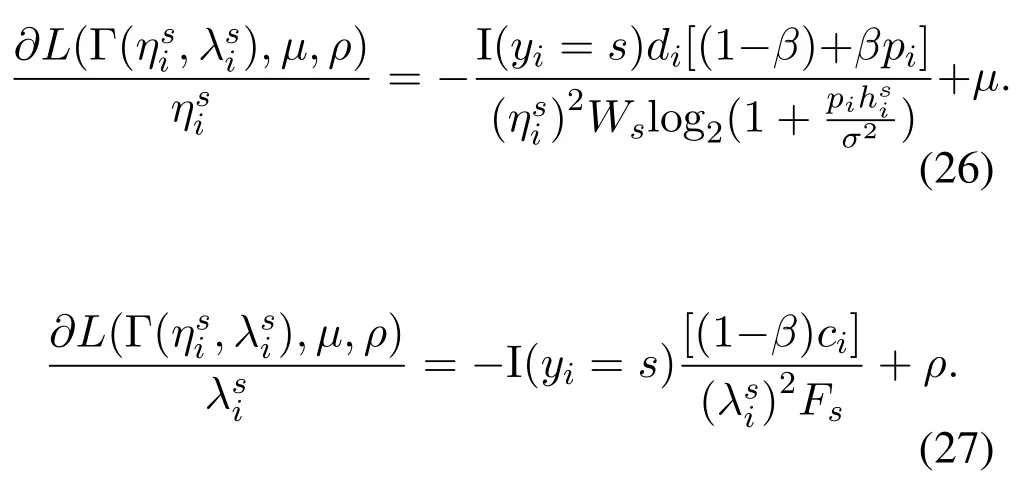
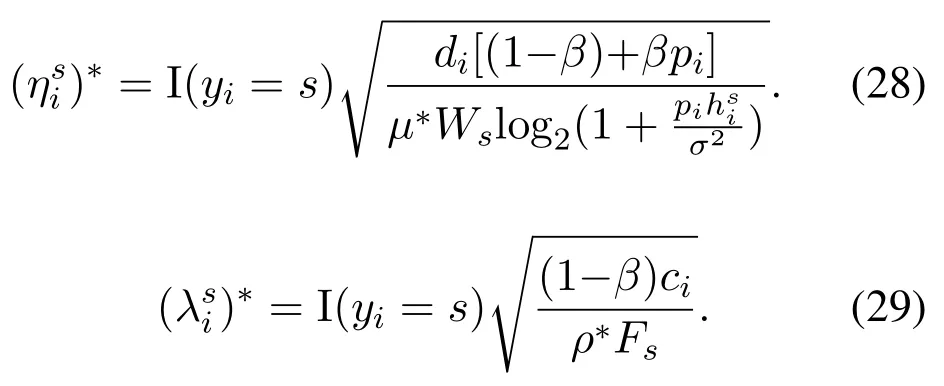
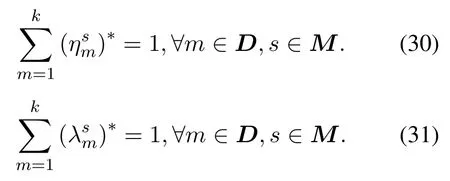
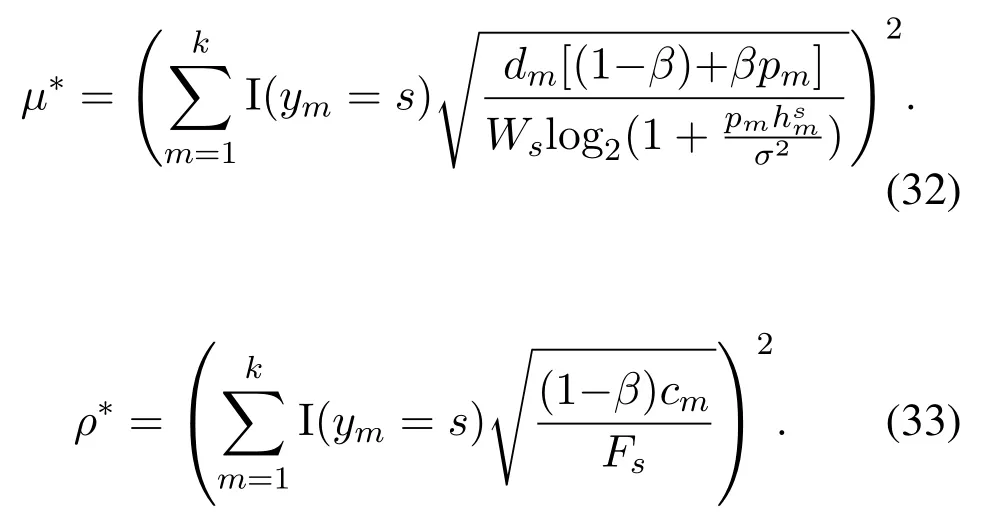
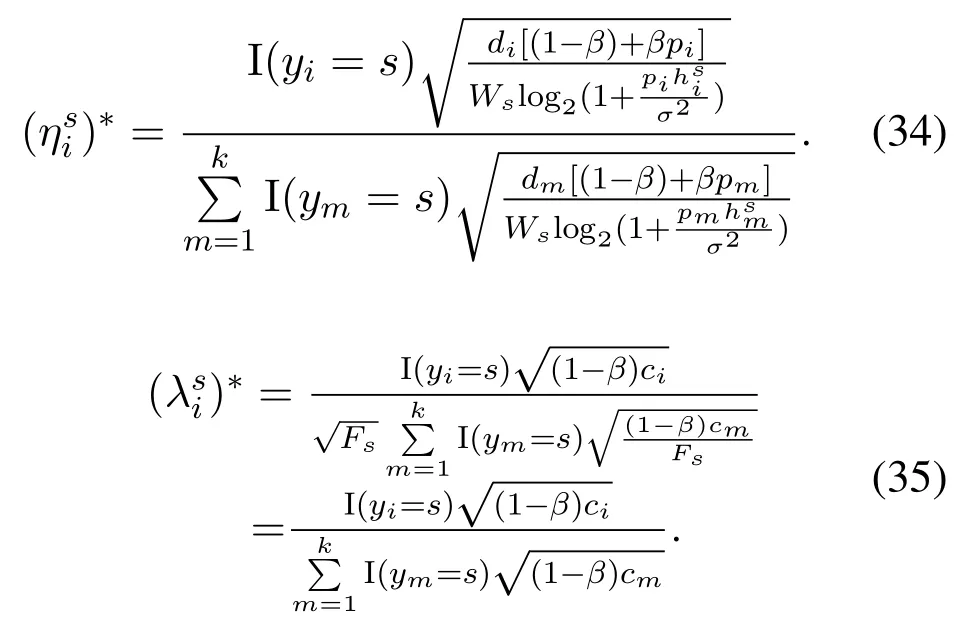
- China Communications的其它文章
- Edge Intelligence for 6G Networks
- Register Allocation Compilation Technique for ASIP in 5G Micro Base Stations
- Deep Reinforcement Learning Based Joint Partial Computation Offloading and Resource Allocation in Mobility-Aware MEC System
- Federated Reinforcement Learning with Adaptive Training Times for Edge Caching
- Paving the Way for Economically Accepted and Technically Pronounced Smart Radio Environment
- Arbitrary Scale Super Resolution Network for Satellite Imagery

