Amplitude and rotation of the ellipticity of harmonics from a linearly polarized laser field
Ping Li(李萍) Na Gao(高娜) Rui-Xian Yu(蔚瑞賢) Jun Wang(王俊) Su-Yu Li(李蘇宇)Fu-Ming Guo(郭福明) and Yu-Jun Yang(楊玉軍)
1Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China
2Jilin Provincial Key Laboratory of Applied Atomic and Molecular Spectroscopy(Jilin University),Changchun 130012,China
Keywords: high-order harmonic,ellipticity,rotation,attosecond pulses
1. Introduction
The interaction of high-intensity laser pulses with atoms or molecules leads to a series of nonlinear phenomena,[1–3]such as multiphoton ionization (MPI),[4,5]nonsequential double ionization,[6,7]above-threshold ionization,[8–11]Coulomb explosions,[12,13]and high-order harmonic generation (HHG).[14–28]HHG is an effective means to obtain desktop shortwave coherent radiation source, and its spectral range has expanded from infrared to extreme ultraviolet band and across the soft x-ray (1 nm–30 nm) band. Moreover,it can be used to generate attosecond pulses and detect the electronic structure of atoms and molecules.[29–32]Attosecond pulse chains and single attosecond pulses generated from HHG.[33–35]provide a tool for the real-time measurement of ultrafast electronic processes in atoms, molecules, and semiconductor nanostructures.
Using a linearly polarized laser field,the ionized electrons of atoms primarily move in a one-dimensional straight line,and harmonic polarization is linear as a result of the recollision of the ionized electron with the parent ion along the polarized direction of the driving laser pulse. Additionally,the polarization direction of the high-order harmonics is the same as that of the incident laser polarization.[36]Recently, strong circularly polarized harmonic radiation has been observed experimentally by using counter-rotating two-color circularly polarized laser pulses interacting with atoms and molecules,[37–40]which can be attributed to the fact that the ionized electrons in this field can return to the parent ion at different angles.Compared with linearly polarized harmonics, circularly polarized harmonics have one more adjustable degree of freedom and potential application in chiral molecules and circular dichroism measurement of magnetic materials.[41–43]Since then, considerable research has been conducted on the generation of circularly polarized high-order harmonics by other combined light pulses, such as circularly polarized HHG by using intense few-cycle elliptically polarized laser pulses and a terahertz field[44]and by combining a fundamental frequency field and an orthogonal second harmonic field.[45]
Recently,studies have shown that the HHG by molecules in a linearly polarized laser field is sensitive to molecular orientation;when the direction of the molecule changes regarding the field, the interference contributions from different atoms in the molecule lead to the suppression of harmonic in a specific frequency band.[46]Leinet al.have calculated the effect of molecular alignment angles on the harmonics of H+2irradiated by a linearly polarized laser field in two and three dimensions. A minimum value caused by an interference effect can be found in all spectra,which moves to a higher harmonic order with the increase of the alignment angle.[47]The harmonics generated do not possess linear polarization characteristics,and their intensities are parallel to the laser polarization direction and perpendicular to the laser polarization direction are comparable. Consequently, circularly polarized harmonics could be generated. Compared with a counter-rotating two-color circularly polarized laser pulse and combined laser pulses, a linearly polarized laser is more convenient. Kimet al.[48]found that H2and H+2irradiated by a linearly polarized laser field would simultaneously generate harmonics along the laser polarization direction and perpendicular to the laser polarization direction. Telnovet al.studied the of MPI and HHG on the alignment angle of H+2, whose internuclear distance is 2.0.[49]Zhouet al.performed precise polarization measurements of the HHG of aligned molecules. They found that harmonics emission can also be strongly and elliptically polarized by N2driven by a linearly polarized laser field.[50]Leet al.investigated the polarization of high harmonics from the aligned N2, CO2, and O2, and the results show that its polarization state depends on the molecular species.[51]Guoet al.found that molecular arrangement can be determined by the harmonic polarization state for the aligned N2molecule irradiated by a linearly polarized laser.[52]Jianget al.investigated the HHG from the aligned CO2molecule driven by a linearly polarized laser and found that the molecular polarization can be determined by the harmonic polarization state.[53]Sonet al.studied elliptically polarized high-order harmonics from aligned molecules irradiated by a linearly polarized driving field,and the physical mechanism of elliptically polarized harmonics is the amplitude and phase of harmonics.[54]However,the generation of elliptically polarized high-order harmonics,modulation of polarization characteristics,and basic principles of molecules driven by linearly polarized lasers must be studied. Thus,we have conducted the following research work.
In this study, we investigated the polarization characteristics of HHG from aligned H+2(the symmetric 1σg orbital)in a linearly polarized laser pulse by numerically solving the time-dependent Schr¨odinger equation(TDSE).We found that the harmonics from H+2irradiated by a linearly polarized laser field change their ellipticities regularly by increasing the alignment angle. As the molecular alignment angle changes from-90°to 90°, the positive and negative changes in the ellipticity of each order harmonic in the platform region are as follows: 0→negative→0→positive→0→negative→0→positive→0. The maximum value of the ellipticity can be close to 1, which is because of the change in the Coulomb force of the ionized electron in the direction perpendicular to the laser polarization. We discussed the change in electronic trajectory caused by the change in the direction of force felt by the ionized electron. Given the change in force direction, selecting a specific alignment angle can produce a nearly circular polarization of harmonics,and the ellipticity of harmonics can also be changed by changing the internuclear distance of the molecule. In this study,we collected harmonics in particular bands and synthesized a single attosecond pulse, whose ellipticity changes regularly with the alignment angle. Unless otherwise specified,atomic units are used throughout this paper.
2. Theoretical model and numerical method

whereRis the internuclear distance,Ais the soft-core parameter,andQis the effective nuclear charge. In the case ofR=2,A=0.52, the ionization energy is-1.1 (29.93 eV), which is the same as that of H+2. The angle between the molecular axis andxaxis isθ. Here we hypothesize that the polarization direction of the linearly polarized laser pulse is along thexaxis.The molecular axis lies in thex–yplane. The laser pulse can be expressed as follows:

wheref(t)is the laser pulse envelope, the shape of the envelope is sin2,andE0andωare the peak amplitude and angular frequency of the laser pulse,respectively.
We obtained the initial wave function by using the virtual time evolution method.[55]Then,Eq.(1)was numerically solved by using the splitting-operator method combined with the fast Fourier transformation. The time and space steps are set to Δx=Δy=0.1 and Δt=0.026,respectively,and the spatial integration grid size is 409.6. The wave function was multiplied by a cos1/8mask function at each time step to avoid unphysical reflection of the wave packet from the boundary.By using the time-dependent wave function,the dipole accelerations in thexandydirections are written as follows:



3. Results and discussion
Figure 1 shows the high-order harmonics generated by the oriented H+2and irradiated by a linearly polarized laser pulse. The wavelength of the laser pulse is 780 nm (corresponding frequency ofω=0.058), and the peak amplitude of the laser fieldE0is 0.11, corresponding to the intensity ofI=4.2×1014W/cm2. The pulse duration is two optical cycles, and the polarization direction is along thexaxis. The molecular axis lies in thex–yplane, and the angle regarding thexaxis isθ. Additionally, figure 1(a) shows the relationship between this angle and the driving laser pulse. When the alignment angleθ=30°, the generated harmonic spectra are the harmonic component polarized parallel to the laser polarization direction(xaxis direction)(solid red line)and perpendicular to the laser polarization direction(yaxis direction,dotted blue line, Fig. 1(b)). Based on this alignment angle,harmonics occurs in the direction perpendicular to the laser polarization direction. At a specific frequency range(such as the range of 22nd to 37th),its intensity exceeds the harmonic component in the direction parallel to the laser polarization direction. Figures 1(c) and 1(d) show the change in the intensity of the harmonic in parallel polarization and perpendicular polarization states with the alignment angle, and the angle increases from-90°to 90°. As shown in Fig. 1(c), the spectrum of the harmonics in the parallel laser polarization direction exhibits a “minimum value” structure as the angle changes. This result is consistent with the conclusion drawn by a previous work, which studies the minimum value of the harmonic spectrum of diatomic molecules driven by the linearly polarized laser field at different alignment angles.[47]Here, we also show the position of the harmonic spectrum minimum(solid red line)calculated by the two-center interference effect formulaRcosθ=(n-1/2)λ,which is consistent with that calculated by quantum simulation. The harmonics in the direction perpendicular to the laser polarization direction change with the angle completely different. Additionally,no harmonic emission is observed when the angle is-90°,0°, and 90°, and the harmonic intensity is the highest when the angle is approximately±45°. Moreover, no “minimum value” characteristic that depends on the alignment angle is found. Therefore,the intensity of harmonics in the perpendicular polarization state reaches or even exceeds that in the parallel polarization case near the frequency band where harmonics in the parallel polarization show a minimum value. If the phase difference between two harmonic components is close to±π/2,then high-order harmonics can be produced close to circular polarization. Furthermore, we analyze the influence of molecular alignment angle on the amplitude and rotation of harmonic ellipticity.
Figure 2(a) shows the ellipticity of the HHG of H+2at different alignment angles irradiated by a linearly polarized laser field. As the molecular alignment angle changes from-90°to 90°, the positive and negative changes in the ellipticity of each order harmonic in the platform region are as follows: 0→negative→0→positive→0→negative→0→positive→0. The maximum value of the ellipticity can be close to 1. The negative and positive values of the ellipticity correspond to the left-handed and right-handed polarized harmonic field in the time domain, respectively, and ellipticity equal to 1, less than 1, and equal to 0 corresponds to the circularly,elliptically,and linearly polarized field,respectively. Moreover, the position where the harmonic appears to alternate left and right rotation(corresponding to the negative and positive alternating change of ellipticity)is the alignment angle corresponding to the“minimum value”of the harmonic and 0°alignment angle.The intensities of the harmonics in the two polarization directions are unchanged, and the phase difference undergoesπjumps. When the electron returns to the nuclear region, the direction of the Coulomb force changes:the force in thexdirection remains unchanged,whereas the direction of the force on theyaxis is the opposite.Consequently,the time-dependent dipole acceleration in thexdirection is almost unchanged, whereas that in theydirection changes negatively and positively. Furthermore,the inverse sign of the time-dependent dipole acceleration in theydirection in the time domain brings about that the time-dependent dipole acceleration undergoes a phase difference ofπin the frequency domain, and finally the rotation reverses. Figure 2(b) shows the ellipticity change of four different order harmonics ranging from a lower frequency to a higher frequency in the HHG platform region to observe the change in ellipticity with the molecular alignment angle. Notably, the amplitude of the ellipticity of the harmonic is equal,and the rotation direction is opposite when the molecular alignment angle is equal in value but opposite in rotation direction. For example, the ellipticity of the 35th harmonic is 0.91 when the alignment angle is-30°,which corresponds to the right-handed elliptic polarization in the time domain. When the alignment angle changes to+30°,the harmonic changes to a left-handed elliptic polarization with an ellipticity of-0.91.Therefore,as the oriented H+2is exposed to a linearly polarized laser field,the harmonic radiation field in the platform region will change with the molecular alignment angle and successive transition to right-handed,linear,and left-handed polarization.

Fig. 1. (a) Relationship between molecules and electric fields, the laser pulse polarized along x axis and propagates along z axis. (b) Harmonic spectrum generated of H+2 driven by linearly polarized laser field when angle is 30° the solid red and dotted blue lines denote the HHG which is polarized along the x axis and y axis. (c),(d)Variation of HHG of H+2 at R=2 in the x and y directions at each order with the alignment angle,respectively,the solid red line shows the“minimum value”structure of harmonic spectrum by the two-center interference.
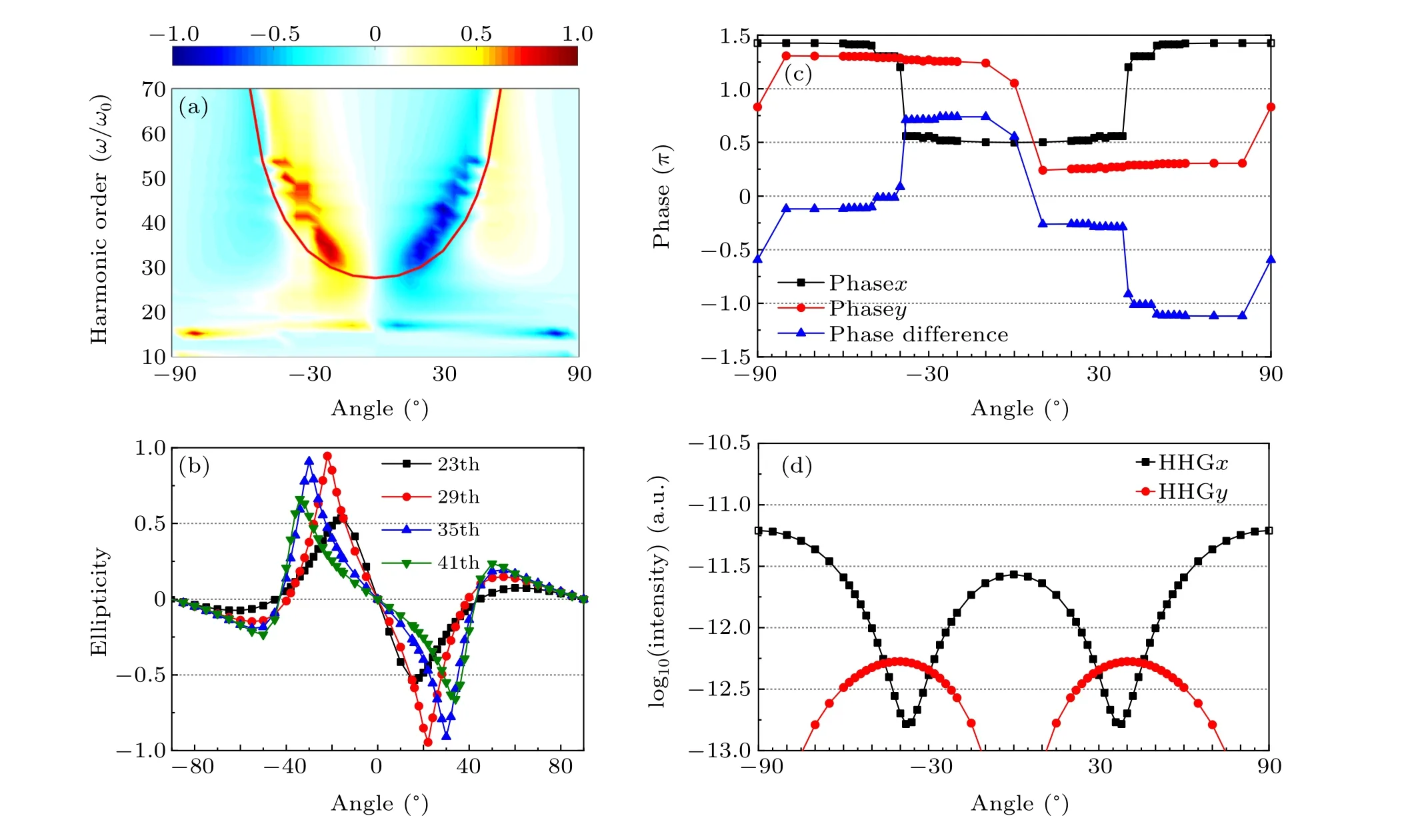
Fig.2. (a)The ellipticity of the harmonics from H+2 driven by linearly polarized pulse as the alignment angle changes from-90° to 90°, (b)ellipticity of 23th, 29th, 35th and 41th harmonics as the alignment angle changes from -90° to 90°, (c) phase and (d) intensity of the corresponding 35th harmonic at different alignment angles.
The polarization characteristics of the harmonic are determined by the intensity ratio and phase difference of the two orthogonal components: When the intensity is the same and the phase difference is odd times ofπ/2, the corresponding harmonic is circular polarization, but when the intensity difference between the components in the two directions is high or the phase difference is integer times ofπ, the corresponding harmonic is linear polarization.We take the 35th harmonic as an example to understand the polarization characteristics of H+2harmonics. Figures 2(c)and 2(d)present the change in the phase and intensity of the 35th harmonic field with the molecular alignment angle,respectively. The black squares and red circles denote the polarization component of harmonics in thexandyaxes, and the blue triangles denote the phase difference between thexandycomponents of the harmonics. The maximum values of the ellipticity of the 35th harmonics appear at the alignment angle of±30°; the harmonic intensity is basically equal in the two directions, and the phase difference of 0.7π, which is close toπ/2. Thus, the amplitude of harmonic ellipticity is high at this angle. However, the phase difference is not exactly equal toπ/2. Therefore, it is only close to circular polarization. Moreover,the phase differences at the alignment angles of+30°and-30°are close to-π/2 andπ/2, respectively, and the harmonics are left-handed and right-handed elliptical polarization in the time domain. For the alignment angle near-90°,0°,and 90°,the harmonics in thexdirection are much stronger than those in theydirection;therefore,the total harmonic is linear polarization.


Fig.3. (a)The-?V(x,y)/?x and-?V(x,y)/?y when the alignment angle is-30° and 30°,(b)force acted on the electron in the the x and y direction as it passes through the nuclear along the x axis at the alignment angle of-30° and 30°, (c)schematic diagram of electron trajectory at the alignment angle of-30°,(d)schematic diagram of electron trajectory at the alignment angle of 30°.
One of the great challenges in the study of circular or elliptically polarized high-order harmonics is how to use them to achieve coherent pulses with isolated attosecond duration in the circular or elliptic polarization states. Here, attosecond pulses with different rotations are synthesized by using the high-order harmonics with different ellipticities generated by changing the molecular alignment angles (Fig. 4). Figures 4(a1)–4(a5) show the time evolution of the attosecond electric field when the molecular alignment angle gradually changes from-30°to +30°, and the corresponding Li Saru graphs correspond to Figs. 4(b1)–4(b5), where black arrows show the rotation direction of the electric field vector over time. In obtaining the isolated attosecond pulse, the phase of the driving field is set as 0.25π, and the attosecond pulse is synthesized from the harmonics from 27th to 50th in the frequency band. The isolated attosecond pulses have a duration of approximately 190 as,whose polarization state changes from right-handed near-circular to right-handed elliptic, then to linear and left-handed elliptic,and eventually to left-handed near-circular when the molecular alignment angle gradually changes. Therefore, attosecond pulses of different polarization states and rotation directions can be synthesized by rotating the alignment angle of the molecular axis.
Finally, the harmonic generated by H+2driven is by the linearly polarized short pulse, the maximum position of the ellipticity appears on the side of the harmonic spectrum minimum in the direction parallel to laser polarization,and its frequency is slightly higher than that at the minimum. Therefore,the frequency corresponding to the maximum value of the ellipticity will move toward higher energy as the alignment angle increases. Additionally, it also varies with the distance between molecular nuclei because the minimum position of the harmonic spectrum of diatomic molecules depends significantly on the internuclear distance under the two-center interference model. Figure 5 shows the distribution of the ellipticity of harmonics from H+2at different orders at alignment angles of-90°to 90°when the internuclear distances areR=1.8,R=2, andR=2.2. The larger region of the ellipticity moves to the lower order direction as the internuclear distance increases. On the contrary,the larger region of the ellipticity moves toward higher order as it becomes smaller.This scheme provides an opportunity for us to synthesize more optimized attosecond pulses under the combined action of molecular alignment angle and internuclear distance or achieve realtime detection of molecular alignment angle and internuclear distance states by using the polarization states of HHG. In this study, the harmonics are generated from the alignment molecules. Certain harmonics will exhibit polarization characteristics under a certain alignment angle, and the mechanism of its generation is explained. For realistic molecular alignment distribution, molecules are distributed randomly at various alignment angles; thus, directly observing harmonics is difficult because of the relatively low efficiency of polarized harmonics.Therefore,initially introducing an alignment pulse and then adding a driving pulse are necessary to generate the polarized high-order harmonics.

Fig.4. [(a1)–(a5)]Isolated attosecond pulses generated by superimposed 27th–50th harmonics generated by H+2 at the alignment angles of-30°,-15°,0°,15°,30° under linearly polarized pulses,[(b1)–(b5)]rotation corresponding to the isolated attosecond pulse generated.

Fig.5. Under linearly polarized laser field,the carrier wavelength of laser field is 780 nm and the laser field peak amplitude is 0.11,the ellipticity distribution of HHG of different orders of at R=1.8,R=2,R=2.2 at-90° to 90° alignment angle.
4. Conclusion
We theoretically simulate the HHG process of H+2irradiated by ultra-short linearly polarized laser pulses by numerically solving the TDSE. The aligned H+2can produce highly elliptic polarized harmonics in this light field. Furthermore,the harmonic polarization state varies with molecular alignment angle and internuclear distance, which can change continuously between left-handed circular polarization,linear polarization, and right-handed circular polarization. Moreover,the change results from the change in the direction of the total Coulomb force of the two nuclei felt by the recollided electrons that emit harmonics,which is perpendicular to the direction of the laser polarization. These harmonics can be used to generate isolated attosecond pulses with different polarization states. This law also provides an opportunity to detect the molecular state in realtime by using the polarization state of the molecular high-order harmonics or attosecond pulses.
Acknowledgments
Project supported by the National Key Research and Development Program of China(Grant No.2019YFA0307700),the Science Foundation of China (Grant Nos. 11627807,11774129,and 12074145),the High Performance Computing Center of Jilin University for supercomputer time,and the high performance computing cluster Tiger@IAMP.
- Chinese Physics B的其它文章
- Design of vertical diamond Schottky barrier diode with junction terminal extension structure by using the n-Ga2O3/p-diamond heterojunction
- Multiple modes of perpendicular magnetization switching scheme in single spin–orbit torque device
- Evolution of the high-field-side radiation belts during the neon seeding plasma discharge in EAST tokamak
- Phase-matched second-harmonic generation in hybrid polymer-LN waveguides
- Circular dichroism spectra of α-lactose molecular measured by terahertz time-domain spectroscopy
- Recombination-induced voltage-dependent photocurrent collection loss in CdTe thin film solar cell

