Design of sign-reversible Berry phase effect in 2D magneto-valley material
Yue-Tong Han(韓曰通), Yu-Xian Yang(楊宇賢), Ping Li(李萍), and Chang-Wen Zhang(張昌文)
School of Physics and Technology,University of Jinan,Jinan 250022,China
Keywords: valley polarization,topological phase transition,half-valley semimetal,quantum anomalous valley Hall effect,first-principles calculations
1.Introduction
Valleytronics offers a versatile platform for fundamental and applied research for spintronics materials due to its additional valley degree of freedom, apart from charge and spin.[1–4]Two-dimensional (2D) hexagonal lattices such as transition-metal dichalcogenides (TMD) are promising valley materials to manipulate charge, spin, and valley degrees of freedom.[5–11]In such materials, owing to the breaking of the space-inversion symmetry (P), phenomena associated with valley contrasting feature can be explored such as valley Hall effect (VHE) and valley-controllable optical selection rules.[12,13]Recent advances in valleytronics focus on generating valley polarization by breaking timeinversion symmetry (T) and thus lifting the degeneracy ofK/K′valleys.[14]Several approaches have been proposed,like optical pumping,[15–17]magnetic doping,[18–20]magnetic proximity effect,[21–23]and applying an external magnetic field.[24–27]Nevertheless,the intrinsic properties have a higher priority than external tunability so as to reach widespread applications in valley-related physics.Hence, intrinsic valleyrelated materials hosting spontaneous valley-polarization are most desirable, thanks to its advantages of robustness, power efficiency,and simplicity in operation.
Recently, break-through of the discovery of 2D ferrovalley (FV) materials,[28]such as 2H-VSe2,[28]VSSe,[29]LaBr2,[30]LaBrI,[31]GdCl2,[32]CeI2,[33]MXenes,[34]and VSi2N4,[35]may lay the foundation for a spin-valley composite paradigm induced by the integrated effects of ferromagnetic(FM)order and spin–orbit coupling(SOC),which could facilitate the observation of anomalous valley Hall effect(AVHE).Furthermore,considering the perspective of potential applications in valleytronics, except for AVHE, the exploration for magneto-valley materials with valley-related multiple Hall effect(MHE)is of significant importance,which can enrich the valley-related physics and emerging quantum states of matter.One exotic valley-related multiple Hall effect is the quantum anomalous valley Hall effect(QAVHE),[36–40]which possesses the interplay between valley and band topology and combines the valley index and quantum anomalous Hall effect(QAHE),[36]making it possible to realize high-performance quantum devices and thus raising an intensive interest in materials science.However,the realization of QAVHE[37]relies on the combination of SOC, band topology and magnetic ordering,which pose a great challenge for the research on potential high-performance valley-controllable quantum computational devices in 2D materials.
Motivated by these challenges, based on first-principles calculations with DFT+Uapproach and strainedk·pmodel,[37]we have predicted single-layer(SL)RuCl2as an FV semiconductor,exhibiting intrinsic FM order and giant spontaneous valley polarization.Interestingly, we found that different electronic correlation strengths (U) and strains (ε)[41–44]make SL-RuCl2transition to different valley-controllable electronic states, including FV to half-valley[45]semimetal(HVS) to QAVHE to HVS to FV state.These different electronic states are connected with valley-controllable signreversible Berry curvature.Remarkably, QAVHE phase,which combines both the features of QAHE and AVHE, can be realized due to band inversions of dxy/dx2-y2and dz2orbitals atK/K′valleys.We further demonstrate that QAVHE phase of SL-RuCl2exists when electronic correlation strength(U) ranges from 2.19 eV to 2.29 eV.Even increasingUexceed this scope,takeU=2.4 eV,we can still observe QAVHE in the strain range of-2.3% and-1.1% by exerting biaxial compressive strain.Similar phase transition and QAVHE have also be reported in MBr2,[43]FeCl2, VSi2P4,[46]VN2X2Y2(X= group-III andY= group-IV elements).These results broaden the avenue for low-dissipation electronics devices,highly promising for valleytronics and quantum computational devices.
2.Computational details
First-principles calculations with spin polarization within DFT are performed by the Viennaab initiosimulation package (VASP).[47–50]The generalized gradient approximation(GGA) with the Perdew–Burke–Ernzerhof (PBE) realization is used to describe the exchange–correlation effect.[51]The energy cutoff is chosen as 550 eV for expanding the wave functions and the total energy convergence criterion of 10-6eV is adopted for static calculations.All the structural parameters are fully optimized until the force on each atom is converged to 0.01 eV/?A.Ak-mesh of 17×17×1 is used to sample the Brillouin zone and a vacuum layer about 20 ?A to avoid the interactions between adjacent direction.To describe the on-site Coulomb interactionUterms of strong correlated Ru 4d electrons,we employed the GGA+Umethod.[52,53]Phonon spectrum is calculated by using 5×5×1 supercell and 5×5×1qgrid based on the density functional perturbation theory(DFPT)approach.[54]The Berry curvatures are calculated using the WANNIER90 package.[55]The edge states are calculated by using the iterative Green function method.[56]
3.Results and dicussion
In analogy to the TMDs, SL-RuCl2possessPˉ6m2 symmetry with aD3hpoint group, which is composed of Cl–Ru–Cl sandwich layer,and each Ru atom has six nearest Cl neighbors,forming a triangular prism lattice,as shown in Fig.1(a).Thus, thePin SL-RuCl2is broken.Figure 1(b) displays the optimized lattice constants of SL-RuCl2with theUvalues ranging from 0 eV to 3 eV.We can see that the calculated constant increases from 3.46 ?A to 3.61 ?A withUincreasing from 0 eV to 3 eV.By calculating the phonon spectrum in Fig.1(c),no imaginary frequency modes are observed, which demonstrates SL-RuCl2is dynamically stable.In addition, we calculated the elastic constants to check the mechanical stability of SL-RuCl2.The elastic tensorCwith thePˉ6m2 point-group symmetry for SL-RuCl2can be reduced to
The calculated results show thatC11andC12are 34.14 GPa and 14.66 GPa, respectively.The calculatedCijsatisfy the Born criteria for mechanical stability,[57]C11>0 andC11-C12>0,which confirms the mechanical stability of SL-RuCl2.
Next, we turn our attention to the magnetic properties of SL-RuCl2.We consider three magnetic configurations,i.e.,nonmagnetic(NM)state,FM state,and antiferromagnetic(AFM) state, as shown in Fig.S1(a) in supporting information, The energy difference as a function ofUis shown in Fig.S1(b).It is clear to see that SL-RuCl2always prefers FM state withUranging from 0 eV to 3 eV,and the magnetic moment unit cell of FM phase is 4.0μBper Ru atom.According to the Mermin–Wagner theorem,[58]the FM order is generally prohibited by thermal fluctuation if 2D FM systems are isotropic.However, the recent discoveries of FM ordering in 2D CrI3[59]and Cr2Ge2Te6,[60,61]with the presence of spinwave excitation gap arising from magnetic anisotropy illustrate that FM ordering can exist at a finite temperature.Thus,to determine the magnetization easy axis of SL-RuCl2,we calculate the magnetic anisotropy energy(MAE)under differentU, as shown in Fig.S1(c).The MAE is defined as the energy difference between the systems with magnetization axis along in-plane (IP) and out-of-plane (OP) direction, namelyEMAE=E100-E001.We can find that SL-RuCl2prefers an OP-FM state whenU <2.41 eV, whenU >2.41 eV, it turns to IP-FM state.
For 2D FM materials, electronic correlations play an important role in its magnetic, valley and topological properties.[62–65]Thus, we investigate the evolution of electronic band structures driven by electronic correlation (U) in SL-RuCl2and the representative electronic band structures without and with SOC are plotted in Fig.S2 and Fig.2,respectively.Also, the evolution mechanism of the energy bandgap induced by differentUis given in Fig.S3.
For a smallU(U=0 eV),SL-RuCl2exhibits an indirect gap semiconductor.The conduction band minimum (CBM)atK/K′valleys are mainly contributed by dz2orbital with the spin-down channel, and the spin-up dxz/dyzorbitals form the valence band maximum(VBM)(Fig.2(a)and Fig.S2(a)).The opposite spin directions of VBM and CBM indicate SL-RuCl2possesses bipolar magnetic semiconductor (BMS) character.With increasingUbeforeU=2.19 eV, the global gap firstly increases and then decreases (Fig.S3(a)), and the orbitals of Ru-dxy/dx2-y2move up relative to Ru-dxzand Ru-dyzorbitals gradually(Figs.2(a)–2(d)).As shown in Fig.2(d),on account ofTandPbroken,both the CBM and VBM belong to the spindown channel,forming FV state with direct gap and the giant energy difference of band gap atKandK′valleys is 246.2 meV(Fig.S3(b)).
AroundU=2.19 eV,as shown in Fig.2(e),the band gap atK′point gets closed,while still have a gap of 254.5 meV atKpoint.The gap closed atK′valley and opened atKvalley indicating an HVS state.Here,taking SOC into account,HVS state indicates the Dirac cone shaped linear dispersion with intrinsically 100%spin valley polarization,[66]highly promising for charge and spin transport due to the mass-free electron mobility.Then we further increaseU(U >2.19 eV),the band gap atK′valley reopens and Ru-dxy/dx2-y2bands continue to move up and thus exchange from VBM to CBM,the Ru-dz2component goes down and from CBM exchanges to VBM, correspondingly (Fig.2(f)).AroundU=2.29 eV, another HVS states inevitably encountered, with the band gap closing atKvalley,but the gap of about 247.1 meV atK′valley (Fig.2(g)).Continuing increasingU, the band gap atKvalley reopens and the CBM and VBM are apart from each other.From the perspective of orbital components, the Rudz2of CBM have been swapped with Ru-dxy/dx2-y2orbitals of VBM atKvalley.Hereafter SL-RuCl2returns to FV again.As can be seen from Fig.2(h), the valley-polarization of SLRuCl2distinctly occurs at the CBM and the giant energy difference of band gap atK/K′valleys is 240.3 meV(Fig.S3(b)).Thus, AVHE with an anomalous velocityva~-(e/ˉh)E×Ωcan be clearly observed(Fig.S4).WhenUis above 2.41 eV,SL-RuCl2turns to IP-FM state(Figs.2(i)and 2(j)).

Fig.2.Orbital-projected band structures of SL-RuCl2 obtained from GGA+SOC+U (U varies from 0 eV to 3.0 eV).Blue circle represents components of Ru-dxy and Ru-dx2-y2 orbitals,red one is for component of Ru-dz2 orbital,and the green one represents Ru-dxz and Ru-dyz orbitals.
Obviously, from the evolution of electronic band structures driven byUin SL-RuCl2, one can see that whenU <2.19 eV, VBM atK/K′valleys is primarily made up of Rudxy/dx2-y2orbitals,while the energy degeneracy between two valleys is lifted and valley polarization apparently occurs at VBM (Fig.2(d)).After the bandgap closing and reopening again atKandK′valleys,the Ru-dxy/dx2-y2orbitals exchange completely from VBM to CBM, and the energy difference of CBM betweenKandK′valleys is larger than VBM contributed by Ru-dz2orbital(Fig.2(h)).
With regard to the spontaneous valley-polarization of SLRuCl2,the underlying physical mechanisms can be attributed to the combining effect of magnetic exchange interaction and SOC.We takeU=2 eV as an example, the degeneracy between spin-up and spin-down channel is broken due to the existence of FM ordering.Since the VBM and CBM are both occupied by electrons with identical spin,we can ignore the interaction between spin-up and spin-down states.Thus,the SOC only involves the interaction of same spin channels,which can be approximately expressed by[33]

From Eq.(3), we can obtain ΔEv=4α.This indicates that valley polarization significantly occurs at VBM (Fig.2(d)).After the completely swapping of Ru-dxy/dx2-y2and Ru-dz2orbitals between VBM and CBM, as the case ofU=2.4 eV,we can infer that ΔEc=4α,thus valley polarization evidently occurs at CBM(Fig.2(h)).It is noteworthy that valley polarization can be reversed as the magnetization is reversed,which is confirmed by DFT results in Fig.S5.When the magnetization along the-zdirection, the spin and valley polarization of carriers is simultaneously switched.From a practical point of view,using intrinsic magnetism to generate valley polarization is more nonvolatile.Additionally,magnetism can be controlled in a fully electric manner,e.g.,by using current pulses through spin torques,[67]which is ideal for device applications.
Our most prominent finding is that SL-RuCl2is an exotic magneto-valley material,which can host several quantum phase diagrams driven byUstarting from FV phase.Such an FV state is highly beneficial to generating, transporting, and manipulating spin currents in spin-valley spintronics.From the above discussion about the evolution of electronic band structures driven byU, we can observe that SL-RuCl2experienced two critical states, namely HVS state, appears atU=2.19 eV and 2.29 eV,where the band gap closes atK′orKvalley while another valley is still in semiconductor status.Along with the band gap reopening asUincreases,the components of VBM and CBM atK/K′valleys also exchanged.This gap close–reopen scenario and interchanging of orbital compositions indicate a transition from trivial to nontrivial topological phase.This topological phase transition is correlated with valley-controllable sign-reversible Berry curvature asUvariates.In order to investigate this phenomenon, the Berry curvatureΩ(k)of SL-RuCl2is calculated based on the Kubo formula,[68]which could be performed with the following expression:
wherenandn′are the band indexes,vxandvyare velocity operators in thexandydirections, respectively.f(n) is the Fermi–Dirac distribution function.φnkandφn′kare the periodic part of Bloch wave function with eigenvalueEnandEn′,respectively.
Figure 3 shows the Berry curvatures withU=2 eV (a),2.25 eV(b),2.4 eV(c),respectively.As shown in Fig.3(a),regarding FV state(U=2 eV),a nonzero Berry curvature occurs aroundK/K′valleys with opposite signs and different magnitudes.WhenU=2.19 eV, FV state experiences a topological phase transition into QAHVE state, bridged by an HVS state.ForU=2.25 eV, the sign ofΩ(k) atK′valley flips(Fig.3(b)).Further increasingU=2.29 eV,Kvalley also experiences a topological phase transition, akin to the case ofK′valley, resulting in the sign change ofΩ(k) atKvalley.With the increase ofU, it transforms from HVS to another FV state.By comparing these two FV states,the sign of Berry curvature atKandK′valleys are quite opposite(Figs.3(a)and 3(c)).Such dynamics of berry curvatureΩ(k)is bound to influence valley-related anomalous transport phenomena, such as AHVE, valley Nernst effect, valley magneto-optical Kerr effect,and valley magneto-optical Faraday effect.[69]
It is remarkable that QAHVE phase in the range of 2.19 eV<U <2.29 eV can be demonstrated by the calculated Berry curvatures in BZ space (Fig.3(b)).Here, the Berry phase takes the same signs atKandK′valleys,but not the identical values.In this way, the edge spectrum calculated with WANNIER90 package shows a single gapless chiral state connecting the conduction and valence bands,consistent with an integer Chern number (C=1), as shown in Fig.4.Different from valley-polarized quantum anomalous Hall effect(VP-QAHE),the CBM,and VBM atK′/Kvalleys are all contributed by spin-down bands with full valley polarization(Fig.4(a)and Fig.S5(b)).When the magnetization is reversed,the edge state changes to the other valley,with an opposite spin and chiral directions,as shown in Fig.4(b),suggesting a very special behavior of the chiral-spin-valley locking for the obtained edge state.This novel quantum state can be detected by using the noncontact magneto-optical technique,[70]and thus highly promising for most practical applications in valleytronics.
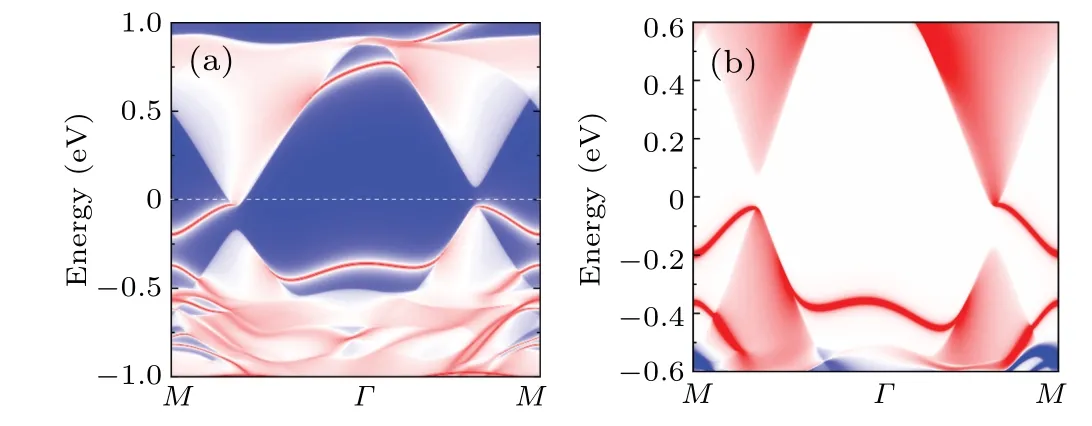
Fig.4.(a)The calculated nontrivial chiral edge states for a semi-infinite SLRuCl2 with U=2.25 eV.The 100%spin-polarized chiral state is locked with the valley index and spin direction.(b) The same as in panel (a), but the magnetization direction is along the-z direction.
Yet for now, it is challenging to regulate the correlation effect (U), but we still hope that the various quantum phase diagram can be exhibited in practice.A crucial point is that the competition between kinetic and interaction energies could influence the strength of electronic correlation, which means we could exert epitaxial strain to manipulate the electronic and magnetic properties of 2D materials and thus probably achieve the same effect as changingU.Therefore, the biaxial strain is applied to the SL-RuCl2.The strain strength is defined asε=(a-a0)/a0, whereaanda0are the lattice constants of the system with and without strain, respectively.Hence, the system of SL-RuCl2can be possibly tuned into FV,HVS,and QAVHE states,even though the electronic correlation strengthUis larger than 2.19 eV.We useU=2.4 eV as an example to explore the quantum phase transitions by exerting external biaxial strain.To confirm the FM ground states, the total energy difference between FM and AFM ordering by using rectangle supercell is calculated as a function ofε, as shown in Fig.S6(a).In considered strain range, the magnetic ground states are always the FM states,And the magnetic anisotropy of SL-RuCl2prefers the OP state under the considered range,as is shown in Fig.S6(b).

Fig.5.(a)The global energy band gap as a function of ε (0%~-4%).(b)The energy band gaps for the K and K′ valleys.
The energy band gap and orbital-projected band structures of SL-RuCl2under various types of biaxial strain are presented in Figs.5 and 6,respectively.With increasing compressive biaxial strain,the gaps at two valleys decreases,whenε=-1.1%, the band gap atKvalley is closed, but it is still open atK′valley, transforming from FV to HVS state(Figs.5(b) and 6(b)).Further increasing compressive strain untilε=-2.3%,the gap atKvalley reopens and closes gradually atK′valley, and the other HVS state can be achieved,as is shown in Fig.6(d).Continuing increasing compressive biaxial strain, the band gap atK′valley will reopen and the system of SL-RuCl2will turn to the other FV state.
In the process of applying biaxial compressive strain,the system of SL-RuCl2also encounters two different critical states, i.e., HVS state, with the band gap closes atKandK′valley, respectively.And the band gap reopening as compressiveεincreases along with the swapping of Ru-dxy/dx2-y2and Ru-dz2orbitals.This exotic transition probably suggests that QAVHE phases exist between the two HVS states.And this strain-induced phase transition mechanism for SL-RuCl2can be explained by constructing ak·pmodel.[35]In order to confirm QAVHE,we calculate the edge spectrum,as is shown in Fig.7.We can clearly observe that a single edge band for connecting the bulk conduction and valence bands,which verifies its nontrivial topology and also indicates a very special behavior of the chiral-spin-valley locking.The QAVHE can also be observed between the two HVS states.With increasing biaxial compressive strain, SL-RuCl2can transform from FV to HVS to QAVHE to HVS to FV state.

Fig.6.Orbital-projected band structures of SL-RuCl2 with SOC under different biaxial strains.Blue circle represents components of Ru-dxy and Ru-dx2-y2 orbitals,red one is for component of Ru-dz2 orbital,and the green one represents Ru-dxz and Ru-dyz orbitals.
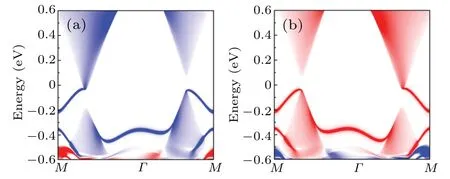
Fig.7.(a) The calculated nontrivial chiral edge states for a semi-infinite SL-RuCl2 with ε =-1.5%.The 100%spin-polarized chiral state is locked with the valley index and spin direction.(b) The same as in panel (a), but the magnetization direction is along the-z direction.
The valley-controllable sign-reversible Berry curvature is also related to the biaxial compressive strain,and we plot the Berry curvatures at some representativeεvalues in Fig.8.For a small compressive strain(ε=-0.7%),as shown in Fig.8(a),we find that a nonzero Berry curvature occurs aroundK/K′valleys with opposite signs and different magnitudes, consistent with the FV state.Under the strain of-1.1%, the sign of Berry curvature atKvalley firstly flips,and then the Berry curvature atK′valley change sign at aboutε=-2.3%.These topological phase transitions are also related to the band inversion of dxy/dx2-y2and dz2orbitals,being similar to variedU.Our understanding of the change of sign for the berry curvature at two valleys is that the opposite and half quantized Hall conductivitye2/2hand-e2/2h,respectively.The phase transition at two valleys happens at two different critical on-site Coulomb interactions:WhenU <2.19 eV,C=1/2-1/2=0;whenU >2.29 eV,C=-1/2+1/2=0, while in the case of 2.19 eV<U <2.29 eV, Berry curvature at one of the two valleys changes its sign and leads a total Chern number as 1/2+1/2=1.
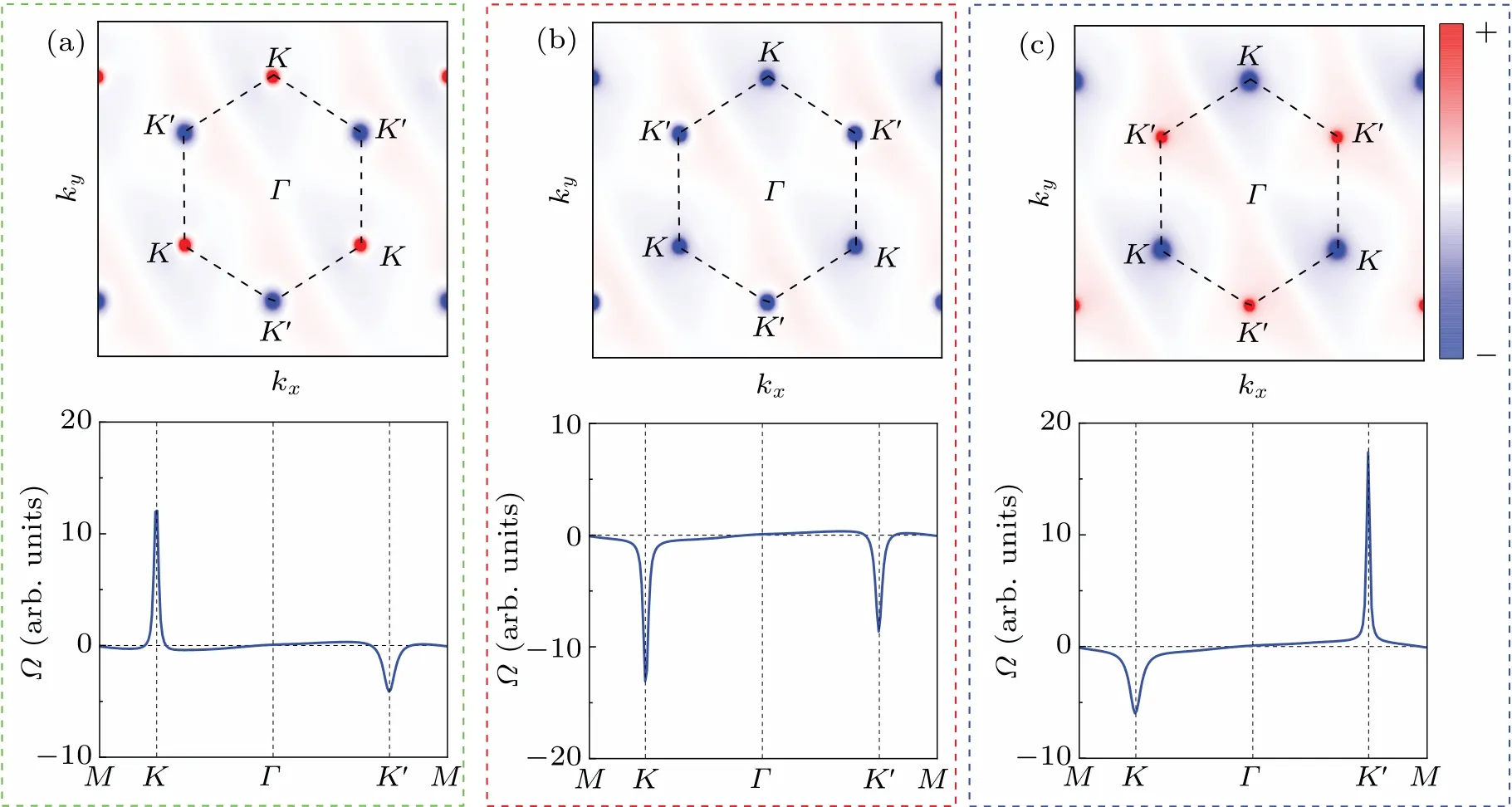
Fig.8.Berry curvature of SL-RuCl2 with ε =-0.7%(a),-1.5%(b),-2.5%(c)at U =2.4 eV.The top planes are contour maps of Berry curvature in the whole 2D BZ,the bottom planes are Berry curvatures along the high-symmetry points.
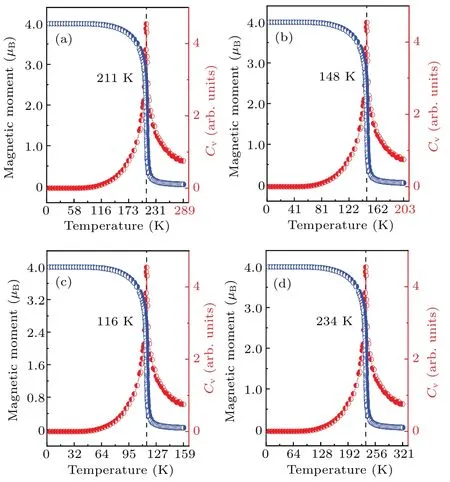
Fig.9.The average magnetic moment and specific heat as a function of temperature with U =2 eV (a), 2.25 eV (b), and ε =0% (c), -4% (d) at U =2.4 eV.
Both electronic correlation effects and compressive strain can effectively tune the strength of FM interaction, which can produce important effects on Curie temperatureTcof SLRuCl2.TheTcis estimated at representativeU(2 eV,2.25 eV,and 2.4 eV)andε(0%and-4%)values with the Wolf algorithm based on the Heisenberg model,which can be expressed as[71]
whereJi,jrepresents the exchange parameters of the nearest neighbor, which could be calculated according to the energy difference between FM and AFM configurations.HereSi/Sjis the spin vector on each Ru,Aiis the anisotropy energy parameter per magnetic atom, andSziis thezcomponent of the spin vector.As the distance between Ru atoms and its second nearest neighboring Ru is more than 6.0 ?A, which is along enough to be ignored, only the nearestJis taken into account.[46]
Thus
On comparing with the energy results from first-principles calculations, the obtained model parameters are found to beJ=4.97 meV andA=117.5 μeV forU=2 eV,J=3.50 meV andA=62.3 μeV forU=2.25 eV,J=2.73 meV andA=0.188 μeV forU= 2.4 eV atε= 0%,J= 5.53 meV andA=158.9 μeV forU=2.4 eV atε=-4%.To make the FMparamagnetic transition clearer,we calculate the heat capacity(Cv)as follows:
Here, ΔETis the change of the total energy as the temperature increases fromTtoT+ΔT.The Monte Carlo simulation is then performed to estimate the transition point of the ferromagnetism,and the results shown in Fig.9.The estimatedTcis about 211 K forU=2 eV,148 K forU=2.25 eV,116 K,and 234 K forU=2 eV atε=0%and-4%.Thus,it is very key for estimatingTcto use reasonableU.And it is found that the compressive strain can improveTc.
4.Conclusions
To summarize,based on first-principles calculations with DFT+Uapproach and ak·pmodel, we found that valleycontrolled quantum phase transitions can be driven by electronic correlation and compressive biaxial strain from FV to HVS to QAVHE to HVS to FV phase in SL-RuCl2.Remarkably, QAVHE and chiral spin-valley, which is induced by sign-reversible Berry curvature or band inversion between dxy/dx2-y2and dz2orbitals,can achieve complete spin and valley polarizations for low-dissipation electronics devices.We also find that this electron valley-polarization can be switched by reversing the magnetization direction, providing a new route of magnetic control of valley degree of freedom.Therefore,our findings not only enrich the research on QAVHE,but also broaden the horizon for the spintronics,valleytronics,and topological nanoelectronics applications.
Acknowledgements
Project supported by the Taishan Scholar Program of Shandong Province,China(Grant No.ts20190939),the Independent Cultivation Program of Innovation Team of Jinan City(Grant No.2021GXRC043),and the National Natural Science Founation of China(Grant No.52173283).
- Chinese Physics B的其它文章
- Dynamic responses of an energy harvesting system based on piezoelectric and electromagnetic mechanisms under colored noise
- Intervention against information diffusion in static and temporal coupling networks
- Turing pattern selection for a plant–wrack model with cross-diffusion
- Quantum correlation enhanced bound of the information exclusion principle
- Floquet dynamical quantum phase transitions in transverse XY spin chains under periodic kickings
- Generalized uncertainty principle from long-range kernel effects:The case of the Hawking black hole temperature

