楊巧艷,廖代琴,顏向平

(蘭州交通大學數(shù)理學院,甘肅 蘭州 730070)

1.引言

隨著生物科學的迅速發(fā)展,越來越多的研究者逐漸意識到時滯對種群生物學的巨大影響,在種群的進化中,時滯是不可避免的.在現(xiàn)實世界里,任何生物種群都處于某一群落中,且與別的種群發(fā)生著一定的聯(lián)系,因此,在不同的種群之間既存在著相互依存,又有相互制約.捕食模型的動力學關(guān)系是生物數(shù)學研究的重要課題之一,至今已有很多學者根據(jù)兩個物種間的相互作用關(guān)系及物種自身的特征建立模型,并對模型的動力學進行了研究.[1-6]考慮到年齡結(jié)構(gòu)與環(huán)境等因素的影響,越來越多的研究開始討論具有時滯的生物模型.如Gopalsamy[7]研究了兩種群具有時滯的競爭系統(tǒng),并建立了共存平衡點的全局穩(wěn)定性結(jié)果.文[8]研究了具有交叉擴散和Holling-II型功能反應的Lotka-Volterra食餌-捕食者模型,討論了在交叉擴散和Holling-II型功能反應聯(lián)合作用下是否存在正解.Alomari和Gourley[9]通過考慮兩成年種群間的相互競爭作用,提出了下面具有時滯的Lotka-Volterra競爭模型

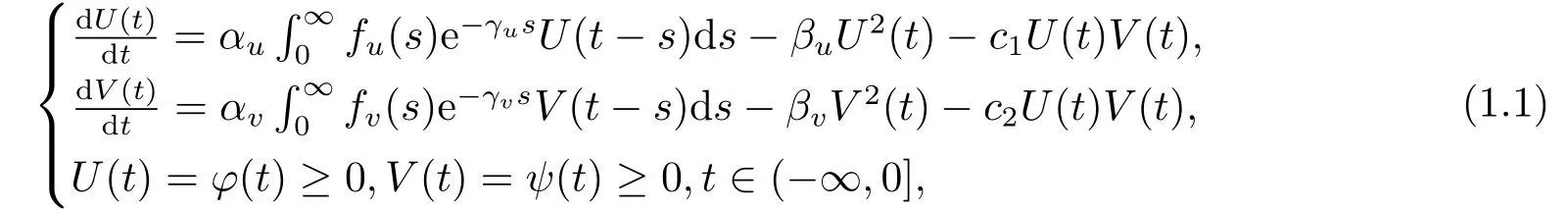
其中U和V分別表示兩競爭種群的成年種群密度;正的常數(shù)αu和αv分別表示兩成年種群的出生率;γu,γv ＞0表示種群在成熟過程中的死亡率;βu,βv ＞0 表示成熟種群的死亡率;c1和c2分別表示兩成年種群間的競爭效應.

利用上下解方法和單調(diào)迭代原理,Alomari和Gourley[9]分析了系統(tǒng)(1.1)平衡點的全局漸近穩(wěn)定性,獲得了當系統(tǒng)(1.1)的一個邊界平衡點線性穩(wěn)定的而另一個不穩(wěn)定時,線性穩(wěn)定的平衡點同時也是全局漸近穩(wěn)定的;當系統(tǒng)(1.1)的兩個邊界平衡點都不穩(wěn)定時,系統(tǒng)(1.1)的共存平衡點是全局漸近穩(wěn)定的.

在自然界中,種群間的相互作用除了競爭關(guān)系外,食餌-捕食者關(guān)系也是一種非常重要的種群關(guān)系.基于此,本文主要考慮具有時滯的Lotka-Volterra食餌-捕食者模型

本文首先利用線性化方法和分析特征根在復平面上的分布情況,獲得了系統(tǒng)(1.2)邊界平衡點的局部漸近穩(wěn)定性,然后利用比較原理和上下解方法證明了系統(tǒng)(1.2)半平凡平衡點和共存平衡點的全局漸近穩(wěn)定性.

2.邊界平衡點的局部漸近穩(wěn)定性

容易看到系統(tǒng)(1.2)總是有可行平衡點

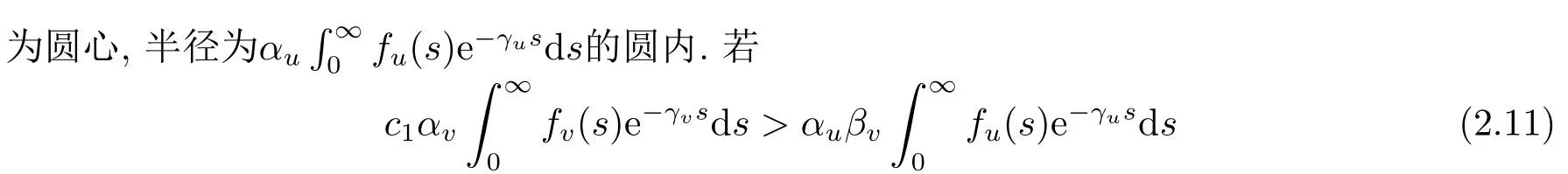
成立,則方程(2.10)的所有根λ具有負實部.因此,當條件(2.11)成立時,系統(tǒng)(1.2)的平衡點是線性穩(wěn)定的.

3.平衡點的全局漸近穩(wěn)定性