潘申潤 陳清華 周曉婷 林 風(fēng)

福建師范大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院 (350117) 福建省福州第三中學(xué) (350025)

《普通高中課程方案和課程標(biāo)準(zhǔn)(2017年版)》(下稱“新課標(biāo)”)作為當(dāng)前教學(xué)的重要依據(jù),立德樹人作為核心素養(yǎng)發(fā)展的重要抓手,將在很長一段時間對考試命題與評價起到根本性的改變．考試對教學(xué)起到引導(dǎo)與反饋的重要作用,也是當(dāng)前檢測學(xué)生學(xué)習(xí)效能與核心素養(yǎng)達(dá)成水平劃分標(biāo)準(zhǔn)的主要手段[1]．高中教材中“探索與發(fā)現(xiàn)”部分的知識也常作為背景出現(xiàn)在考試中．

1 仰觀試題之高端

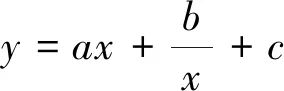
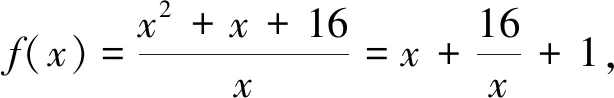
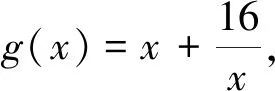
評價：當(dāng)前在基于核心素養(yǎng)的試題命制的基礎(chǔ)上,我們需要注意的是本題重點考察的是學(xué)生的數(shù)學(xué)抽象和直觀想象能力．本題命題重點是:(1)強(qiáng)調(diào)學(xué)生能夠通過具體的問題抽象地分析與研判其背后的規(guī)律,在此基礎(chǔ)上運(yùn)用數(shù)學(xué)語言進(jìn)行表征,即學(xué)生對于“未知但親切”的函數(shù)g(x),能夠?qū)⑵洳鸱殖蒰1(x)與g2(x)通過分析二者的值域進(jìn)而研究g(x)的性質(zhì);(2)基于高中課程的學(xué)習(xí)進(jìn)一步增強(qiáng)數(shù)形結(jié)合的能力,通過“代數(shù)幾何化”發(fā)展幾何直觀能力,在直觀感悟中體會事物的本質(zhì),即學(xué)生直觀地看到g1(x)與g2(x)后能夠進(jìn)一步分析和研究出函數(shù)g(x)的性質(zhì)．

2 俯察教材之基礎(chǔ)

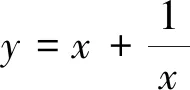
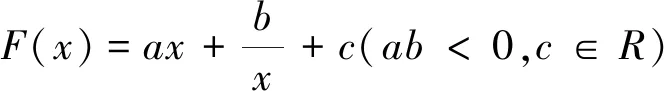
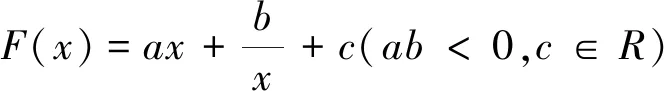
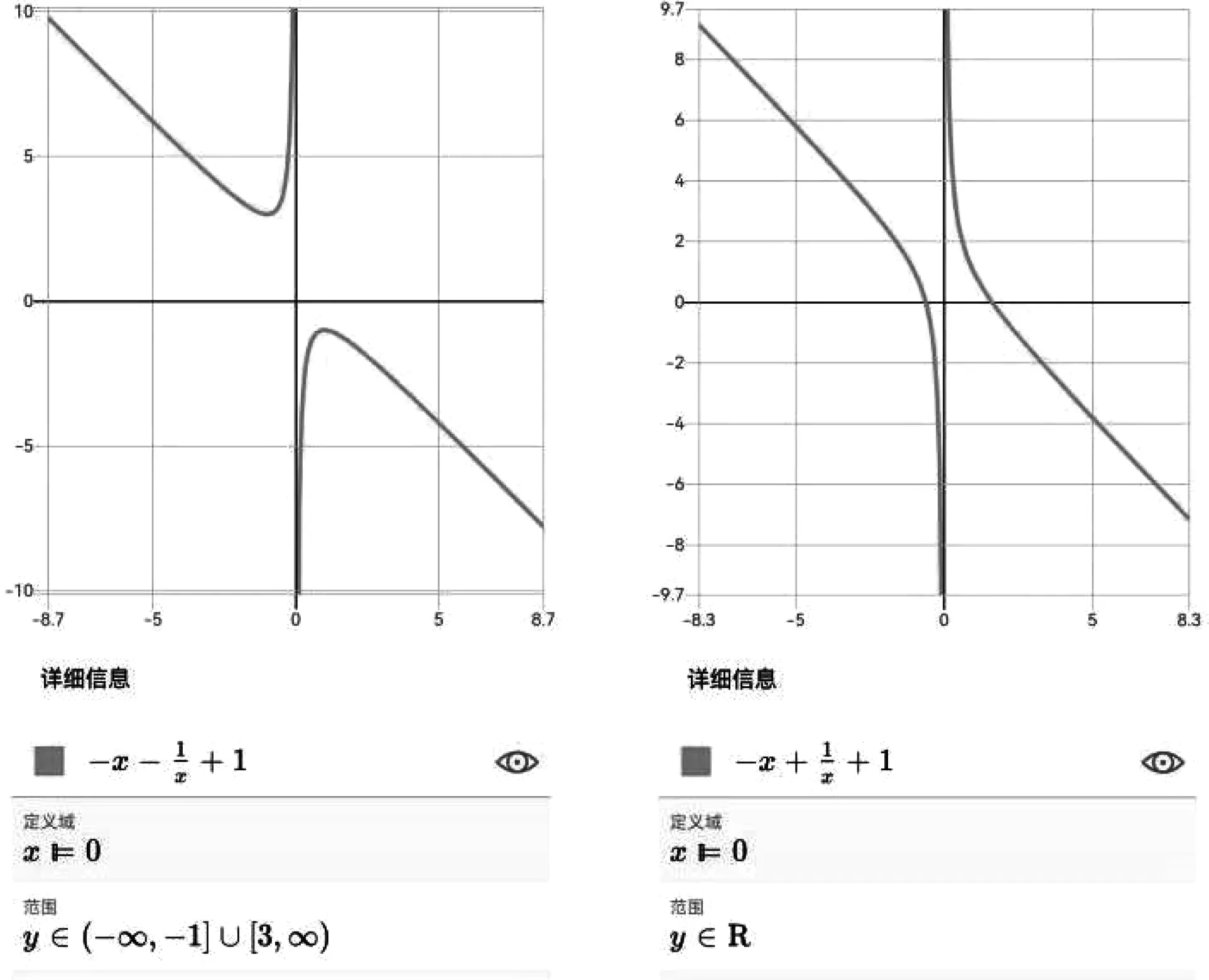
c.a=1,b=-1 d.a=-1,b=1圖1 取c=1時,隨a,b變化F(x)的函數(shù)圖象

a.a=1,b=1 b.a=1,b=1

特別的是教科書中只給出了圖1(a)的函數(shù)圖象,且也未深入研究F(x)的其他性狀,此處我們結(jié)合定理1～4與圖1以作拓展．以下以該結(jié)論作為二級結(jié)論解答幾道聯(lián)賽試題的變式．

分析：由定理2,f(x)的函數(shù)圖象可根據(jù)兩條漸近線(y=4x與x=0)限定其范圍;g(x)為一偶函數(shù),故可先繪制x>0部分,漸近線為y=x2與x=0．

解：函數(shù)圖象如圖2所示．

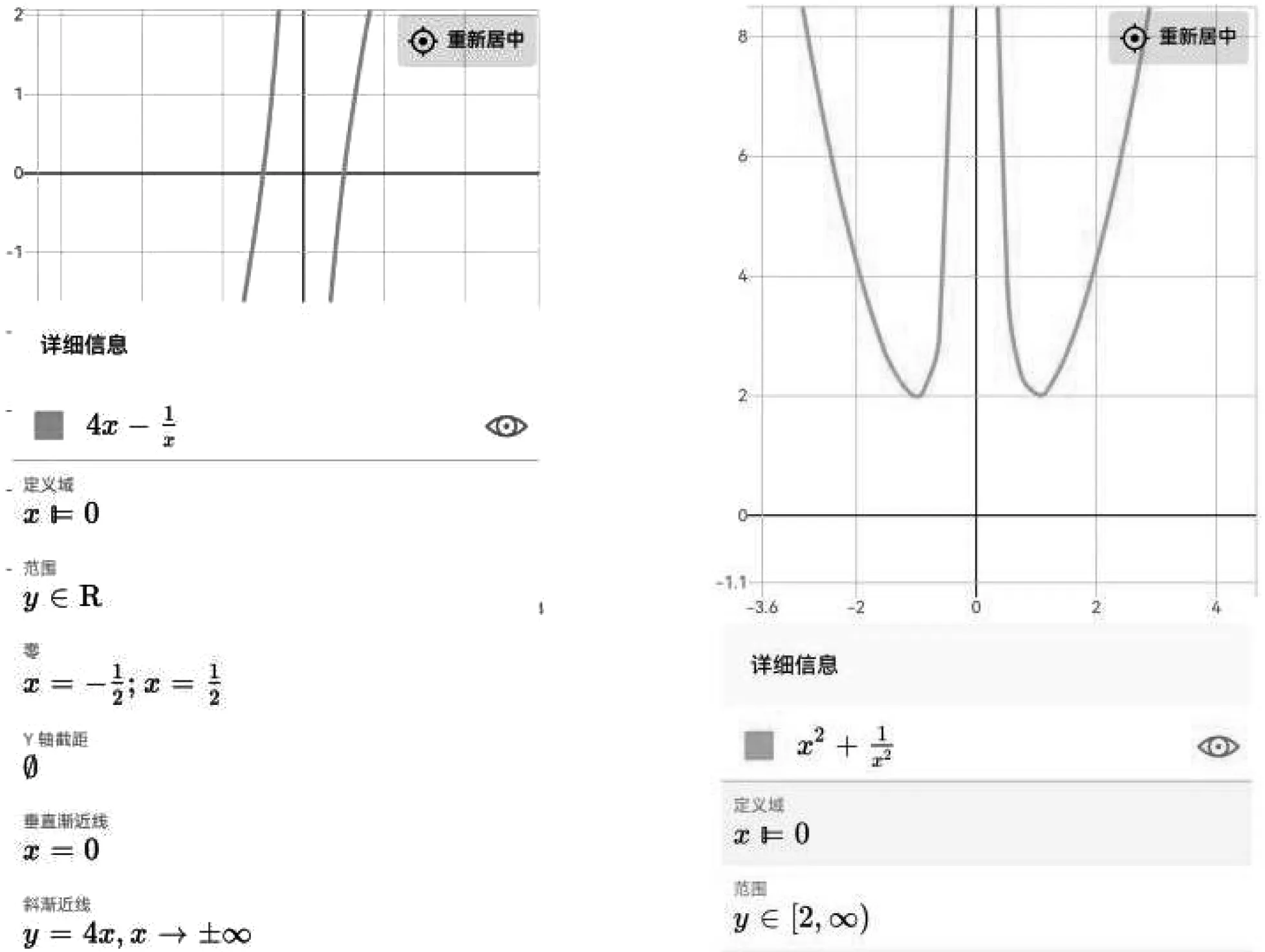
圖2 變式1函數(shù)圖象

3 總結(jié)與展望