Resolution-enhanced single-pixel imaging using the Hadamard transform matrix
Shu-Hang Bie(別書航), Chen-Hui Wang(王晨暉), Rui-Bing Lv(呂瑞兵), Qian-Qian Bao(鮑倩倩),Qiang Fu(付強), Shao-Ying Meng(孟少英), and Xi-Hao Chen(陳希浩)
Key Laboratory of Optoelectronic Devices and Detection Technology,College of Physics,Liaoning University,Shenyang 110036,China
Keywords: single-pixel imaging,Gaussian filtering,resolution enhancement
1.Introduction
Single-pixel imaging(SPI)is a newly developed computational imaging technique,[1-3]which can reconstruct a highdimensional image by various reconstruction algorithms including correlated imaging (also well known as ghost imaging (GI))[5,6]and compressed sensing (CS)[7]by only utilizing one-dimensional (1D) single-pixel signals with the help of the default synchronizing modulation patterns.Because of this special imaging mechanism, it can image a target object in harsh environments such as extremely weak light,[4]atmospheric turbulence[8]and scattering media[9]just as traditional GI can do.[10]Currently,besides performing in the visible spectrum,SPI has demonstrated its viability in exotic regions of the electromagnetic spectrum,such as infrared,[20,21]terahertz,[31-34]x-ray[22,29]and neutron,[23]where conventional imaging techniques face difficulties in both practicality and cost.In 2008, two different imaging schemes of passive and active (it is also well known as computational GI(CGI)) SPI systems were proposed by Duarte’s group and Shapiro,[1,2]respectively.Later, although the idea of active SPI, i.e., CGI comes from traditional GI, an agreement was gradually reached that they were equivalent in imaging principle, modulation strategy and reconstruction method except that the positions of the light source, the spatial light modulator(SLM),the object and so on are different in the imaging setup.
Different modulation methods have been proposed and implemented for SPI schemes using both digital micromirror devices (DMDs) and SLM technologies.[11-43]Initially, nonorthogonal random patterns were used to modulate the optical field in SPI.[11-14]However, this approach was associated with issues such as long data acquisition time and low reconstruction quality.As SPI continued to develop, it was found that deterministic model-based techniques could effectively address these issues.The two representative modulation schemes are those based on the Hadamard bases[15-38]and Fourier bases,[39-43]respectively.They are able to achieve almost perfect reconstruction of the target scene by taking advantage of these basis patterns from a complete orthogonal set,[44]which effectively overcomes the problem of low reconstruction quality.In addition, they can also reconstruct clear images from the under-sampled data by utilizing the fact that the measurement basis is sparse in different representations.Over more than a decade,there have been many reports about the ordering of these basis patterns in SPI.[16-18,53-55]Besides various CS and CS-based SPI schemes,[24,25]SPI via deep learning[26-30]has been also proposed to not only improve the quality of reconstructed images but greatly reduce the sampling number.
In the following study, except for the above basis patterns used in SPI, some schemes have been proposed to generate various customized speckle fields.[46-51]In 2014,Cao’s group proposed a versatile method for generating non-Rayleigh speckle patterns.The method involves encoding higher-order correlations into the optical by the phase-only SLM which results in a redistribution of light intensity among the speckle grains in the far field.[46]In recent work, they found that the non-local correlation introduced by tailoring the intensity probability spectral density of the speckle patterns can exceed the resolution limit.[47,48]Moreover, an approach of generating the speckle patterns by different noise modes was proposed in the perspective of power spectral density (PSD),[51,52]where a computational GI-like experiment was realized based on a binary-modulated DMD.It is found that there are special spatial intensity fluctuation correlations between adjacent pixels of these speckle patterns,which helps achieve better noise robustness or higher spatial resolution in CGI systems.[51,52]However, almost all of these schemes of generating customized speckle fields required a certain complicated transformation to obtain speckle patterns and then project these on the modulation device.This is greatly limited by the accuracy of a modulation device such as DMD when the modulation patterns have to be not binary.Therefore,although the transformation of some standardized modulation,patterns may theoretically make the performance of SPI improve,there is still a limitation of hardware in an actual experiment.
In this paper we propose a novel SPI scheme to achieve a high-resolution image,which is based on the cross-correlation between the standard binary Hadamard modulation bases and their transformation patterns.Here, the DMD is modulated by standard binary Hadamard bases.Merely by a computational processing, each Hadamard transform pattern can be acquired by an inverse Fourier transform on a Gaussianfiltered Hadamard basis in the frequency domain.Based on the cross-correlation between the bucket signals acquired by actual modulated standard Hadamard bases and their corresponding synchronized transform patterns,a higher-resolution image could be restored just according to a traditional GI algorithm.
2.Theory and method
The principle of a passive SPI is shown in Fig.1,where an illuminating optical beam from a light-emitting diode (LED)passes through an object and enters a lens-imaging system,then an image of the object is imaged on a DMD.The light beam is reflected and converged into a single-pixel detector after it is modulated by the DMD.As we know,the key point of correlated SPI is the correlation between the modulation matrices and the single-pixel signals.Thus in this section we will start from the second-order correlation function of modulation matrices to study the correlation of Hadamard transformation matrices,the cross-correlation between the Hadamard bases and the corresponding transformation matrices,and enhanced resolution by using the latter.To simplify the calculation without loss of generality, only the 1D SPI is considered here,where the intensity correlation functionG(2)(?x)of modulation bases can be expressed as
Here ?xis the relative distance inx.Currently,the DMD is the most commonly used SLM in SPI systems due to its superior modulation rate, and broadband wavelength response.Compared with the Fourier basis,the Hadamard basis is more suitable for loading on DMD without a quantization error because of its binary characteristics.[45]Here the correlation function of Hadamard-based matrices can be simplified as

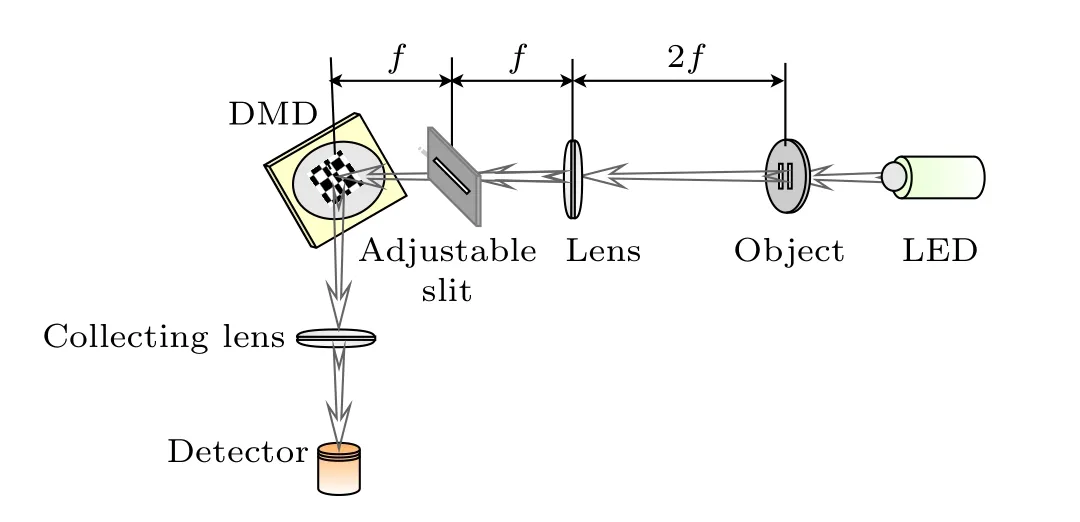
Fig.1.Diagram of experimental setup of SPI.
Actually, the transformation of modulated matrix is a standard process of matrix computation.Firstly, each Hadamard matrixI(ω) in the frequency domain is obtained by a spatial Fourier transform ofI(x).And then the filtered matrixIF(ω) is acquired by Gaussian high-pass filtering for eachI(ω),i.e.,
whereHHP(ω) is a Gaussian function likeHHP(ω) =A0-exp(-ω2/ω0).HereA0andω0are constants set in the function.Finally, eachIF(ω) would be converted intoIF(x) by an inverse Fourier transform, which will be used to correlate with the bucket signals.It is shown in Fig.2 that the correlation between the individual pixels in the filtered matrix is changed with the change of the low-frequency components of the Hadamard matrix.According to the Wiener-Khinchin theorem,the second-order correlation functionG(2)F (?x)after Gaussian filtering can be written as
whereδ(ω)is the average PSD of Hadamard-based patterns.Based on this equation,the auto-correlation of transformation matrix is simulated, whereA0andω0are set to 3 and 8, respectively,and the simulation result is as shown in Fig.2(b).It can be seen that negative correlation dips come out around the correlation peak,which will lead to resolution improvement in SPI.
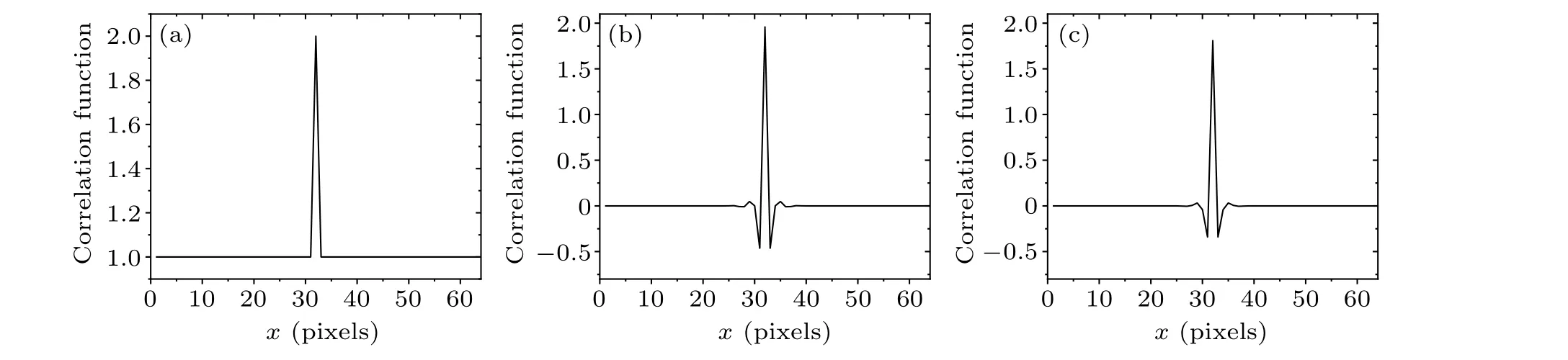
Fig.2.Auto-correlation functions of(a)the Hadamard matrix and(b)transformation matrix;(c)cross-correlation function between Hadamard and their transformed matrix.
In the proposed scheme, the image is reconstructed by the cross-correlation of the Hadamard transformation matrices and the bucket signals that are obtained by using the Hadamard matrices to encode and sample the object.Therefore,the correlation functionG(2)
HF(?x)is accordingly modified by
which is also used to simulate the correlation in Fig.2(c).It is similar to Fig.2(b)that significant spatial cross-correlation dips also exist around the correlation peak, which means that new background noise will be formed near the object when the object image is reconstructed.
In an actual SPI system,thei-th modulated patternIi(x,y)(1≤x ≤M,1≤y ≤N)withM×Npixels is generally a twodimensional discrete matrix.Therefore,thei-th bucket signalBiacquired by the single-pixel detector can be expressed as

3.Simulations and experiments
3.1.Simulation results
In order to demonstrate the effectiveness of the proposed method,an SPI simulation experiment is first performed based on the scheme in Fig.1.In the present simulation, a binary three-slit picture with a size of 64×64 pixels is selected as the imaged object shown in Fig.3(a).The image in Fig.3(b)is obtained by Gaussian low-pass filtering for Fig.3(a),which obviously became blurred because of the loss of spatial highfrequency components of light carrying the information of the object.It is noted that the low-pass filtering for Fig.3(a)should be regarded to mimic a diffraction-limited SPI system and the image of Fig.3(b)is equivalent to the one that is projected on the DMD in a passive diffraction-limited SPI experiment.In the simulation process of SPI,the bucket signals are simulated as follows.The fuzzy image of Fig.3(b) is convolved with each computer-generated Hadamard matrix, and then each convolution pattern is summed pixel by pixel to get a series of 1D bucket signals that are actually captured by a single-pixel detector in an experiment.The corresponding reconstructed images are shown in Figs.3(c)and 3(d)according to Eqs.(7) and (8), respectively.It can be seen that the image of Fig.3(c) recovered by Hadamard matrices is almost as blurred as Fig.3(b) while the image of Fig.3(d) is more resolved and distinguished, which is retrieved by the correlation between the Hadamard and their transformed matrices.It should be noted that the Hadamard matrix that we use is the optimized ordering of the Hadamard basis by using fast Walsh Hadamard transform.[16]To further verify the proposed scheme,an object with two Chinese characters in Fig.3(f)that is a shortened form of Liaoning University is substituted for Fig.3(a)to perform the same simulation experiment.The experimental results of simulations are shown in the second row of Fig.3,which are quite similar to the results of the first simulation as predicted.It is not a surprise that the blurred images can be resolved and distinguished more clearly by the proposed method.When the transfer function in the diffraction system is invertible and known,the higher-resolution image can be reconstructed by the deconvolution just shown in Fig.2.However, it is obvious in Figs.3(d) and 3(i) that additional background noise is also brought in the reconstructed images due to the negative correlation,which would form socalled “virtual” images near the real images that may lead to the image degradation and the decreasing of SNR.Therefore,a simple spatial high-pass filtering method is adopted to remove the background noise, where a properly chosen threshold that is determined by the direct current background of the recovered images is set to subtract the negative background.The background-subtracted images are shown in Figs.3(e)and 3(j), where they have been remapped to a grayscale range of 0-255.

Fig.3.First column: digital-imaged objects of binary pictures with (a)three slits and (f) two Chinese characters.Second column: (b) and (g)are low-pass filtering of (a) and (f), respectively.Third column: reconstructed images of(c)and(h)for the images in the second column based on Eq.(7).Fourth column: reconstructed images of(d)and(i)based on Eq.(8).Fifth column: background-free images of(e)and(j).
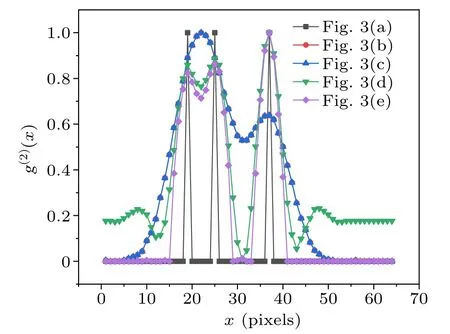
Fig.4.Cross-sectional images of Figs.3(a)-3(e).
In addition, how much the proposed scheme can improve the image resolution is necessary to be much concerned.Therefore,the cross sections of the first row of Fig.3 are plotted in Fig.4 to further explain this problem, where they are represented by the black,red(covered by the blue line),blue,green and purple lines, respectively.Here, it can be more clearly seen that the proposed scheme can achieve a highresolution image with a better SNR, where the two slits on the left are just distinguished while the two slits on the right are completely discernible (see the green and purple lines).Honestly, the spacing distancesW1andW2of the three slits in Fig.3(a)are specially designed to talk about the diffraction limit and super-resolution.It is clear in Fig.4 that the two slits on the right of the blue line are just resolved whenW1=12 pixels,which can be considered as the diffraction limit according to the definition of Rayleigh diffraction bound for the case of Hadamard patterns.The left two slits with a spacing width ofW2=6 pixels are used to test the resolution limit in our scheme,where they are just resolved,too.Thus,it is estimated that the proposed method can exceed the resolution limit by a factor of about 2.
3.2.Experimental results
For the purpose of further verifying the feasibility and performance of our method, a typical diffraction-limited SPI experiment is demonstrated with respect to the configuration in Fig.1, where an object of a double-slit with a slit spacing ofW=2 mm illuminated by a white light LED is imaged on the DMD(V-7000/ViALUX)by an imaging lens with a focal length off= 100 mm.One of the reflected light beams by DMD is totally captured by a single-pixel detector(DET36A2/Thorlabs)with the help of a collecting lens.In addition, a slit with an adjustable widthlis co-axially inserted at the rear focal plane, which is used to form a diffractionlimited imaging system by blocking the spatial high-frequency components of light carrying the object information.The signal from the single-pixel detector is fed into an amplification circuit including a signal-amplifier and an analog-digital converter,and then the signal from the amplifier circuit is finally saved to a computer to be processed via a data acquisition card.Generally, Hadamard bases with a sampling number of the Nyquist limit are in advance stored in the memory of DMD, and the SPI experiment is also realized at a sampling rate of 100%.The results for different sampling rates(including under sample and 100%sample)of different methods are compared and discussed in data post-processing.Here, the sampling number of 32×32=1024 is chosen in the present experiment, which means the size of the modulation matrix is also 32×32 pixels.Notice that the ordering of Hadamard basis is the same with the above simulations.[16]

Fig.5.The reconstructed images by Eq.(7) with different slit widths l=(a)30 mm, (b)0.3 mm; (c)the reconstructed image by Eq.(8), and(d)the background-free version of panel(c).
Two different settings oflare studied here, i.e.,l=30 mm andl=0.3 mm,corresponding to the non-diffractionlimited and diffraction-limited systems, respectively.The reconstructed images by Eq.(7)are shown in Figs.5(a)and 5(b).Apparently, two slits in Fig.5(a) are quite clearly resolvable while those in Fig.5(b) are almost overlapped and become blurred.Figure 5(c) is the reconstructed image achieved by the proposed method based on Eq.(8).Though the image seems to have more noise caused by the decrease of optical intensity when smallerlis preferred,two slits can be perfectly distinguishable.Of course, negative background noise also exists inevitably due to the cross-correlation.However, the clearer background-free image is achieved by removing the background noise and shown in Fig.5(d).The experimental results are in good agreement with the simulations.
4.Conclusion
In conclusion,we have successfully performed a computational GI experiment by correlating a series of bucket signals obtained from a single-pixel detector with the synchronized transformed matrices of modulating DMD Hadamard bases.Our experiment revealed the observation of anticorrelation phenomena between the Hadamard bases and their transformed counterparts, as well as the bunching effect between them.Furthermore, we were able to improve the resolution of the reconstructed image.The proposed approach for achieving high-resolution imaging is solely based on a passive SPI setup and does not rely on the accuracy of the modulated device or complex imaging systems.The transformation of the matrix and image reconstruction are carried out by postprocessing of the computation, which makes this scheme applicable to various mature SPI systems that have been extensively studied.Despite the presence of additional background noise due to negative correlations,a clearer reconstructed image can be obtained through spatial filtering to remove most of the noise.This approach offers an SPI method for achieving high-resolution imaging without increasing the complexity of the SPI system, and may be suitable for use in combination with different imaging systems.
Acknowledgments
We thank Prof.L.A.Wu for helpful discussions.Project supported by the National Key Research and Development Program of China(Grant No.2018YFB0504302).
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Si-Ge based vertical tunnel field-effect transistor of junction-less structure with improved sensitivity using dielectric modulation for biosensing applications
- Speeding-up direct implicit particle-in-cell simulations in bounded plasma by obtaining future electric field through explicitly propulsion of particles
- Temperature-induced logical resonance in the Hodgkin-Huxley neuron
- Energy-distributable waterborne acoustic launcher for directional sensing
- Structural stability and ion migration of Li2MnO3 cathode material under high pressures

