Amina MAZIGHI, Hind MEDDI, Mohamed MEDDI*, Ishak ABDI,2,Giovanni RAVAZZANI, Mouna FEKI

1 Higher National School of Hydraulics of Blida, Blida 09000, Algeria;

2 Department of Civil Engineering and Hydraulics, University of Jijel, Jijel 18000, Algeria;

3 Department of Civil and Environmental Engineering, Polytechnic University of Milan, Milan 20133, Italy

Abstract: Infiltration is an important part of the hydrological cycle, and it is one of the main abstractions accounted for in the rainfall-runoff modeling.The main purpose of this study is to compare the infiltration models that were used to assess the infiltration rate of the Mitidja Plain in Algeria.Field infiltration tests were conducted at 40 different sites using a double ring infiltrometer.Five statistical comparison criteria including root mean squared error (RMSE), normalized root mean squared error(NRMSE), coefficient of correlation (CC), Nash-Sutcliffe efficiency (NSE), and Kling-Gupta efficiency(KGE) were used to determine the best performing infiltration model and to confirm anomalies between predicted and observed values.Then we evaluated performance of five models (i.e., the Philip model,Kostiakov model, Modified Kostiakov model, Novel model, and Horton model) in simulating the infiltration process based on the adjusted performance parameters cited above.Results indicated that the Novel model had the best simulated water infiltration process in the Mitidja Plain in Algeria.However, the Philip model was the weakest to simulate the infiltration process.The conclusion of this study can be useful for estimating infiltration rate at various sites using a Novel model when measured infiltration data are not available and are useful for planning and managing water resources in the study area.

Keywords: infiltration rate; infiltration model; double ring infiltrometer; Mitidja Plain; Novel model

1 Introduction

Infiltration refers to the process of water entering the soil or rock layers from the surface.This phenomenon can occur naturally, for example, through precipitation, or it can be facilitated through human activities such as irrigation or watering plants (Angelaki et al., 2021).Infiltration of water into the unsaturated zone is one of the most important components of the hydrologic cycle (Iovino et al., 2017).Over the last few decades, several physical and empirical models have been developed to quantify the infiltration process, particularly for one-dimensional vertical infiltration (Mishra et al., 2003).The Richards (1931) equation is one of the classic physical models for calculating semi-infinite, isotropic, and stable soil infiltration processes.Infiltration rate depends on the nature of the soil (proportions of sand, silt, and clay) and the mineralogy of clay.Water moves faster through the large pores of sandy soil than through the small pores of clay, especially when the clay is compacted and has little or no structure or aggregation (Schumann, 1998).These soil infiltration properties are determined when mathematically fitting an infiltration model (Thomas et al., 2020).But not all infiltration models are suitable for all soils (Oku and Aiyelari, 2011).Many researchers compare the accuracy of different models by comparing calculated and observed infiltration rates.Under different conditions, a particular model will show better prediction than others.But so far,there is no explicit mention of which model gives the best prediction (Kumar and Sihag, 2019).Many studies have been done for comparison of different infiltration models.The Kostiakov and modified Kostiakov models were the most efficient in estimating the infiltration rate and cumulative infiltration, respectively.The Kostiakov model was most suitable for assessing plain in the Okhlal landfill, Delhi, India.The ability of new infiltration model to estimate infiltration from actual field data was investigated in comparison with the Philip, Kostiakov, Horton, SCS, and modified Kostiakov models under similar conditions (Jain and Chakma, 2023).

Infiltration plays a crucial role in irrigation because it determines how efficiently water is absorbed by the soil and made available to crops.If the infiltration rate is too slow, water can pool on the surface and cause runoff, which can lead to soil erosion and water loss (Adeniji et al.,2013).On the other hand, if the infiltration rate is too fast, water may not be retained in the soil long enough for plants to absorb it, resulting in water stress for crops.By measuring and managing infiltration, farmers can optimize their irrigation practices and ensure that water is used effectively and efficiently to promote crop growth and yield (Thomas et al., 2020).

This research aims to experimentally estimate and compare soil infiltration rate in the Mitidja Plain in Algeria and five different infiltration models, i.e., Novel, Kostiakov, modified Kostiakov,Philip, and Horton.For this study, a number of specific sites within the region were selected and samples were collected from those sites.The infiltration rate was determined by a double ring infiltrometer.Statistical analyses were performed to compare infiltration models and infiltration rate observed.This study is the first step in a project aimed to improve irrigation water use and evaluate irrigation systems in the Mitidja Plain.

The Mitidja Plain is a traditional irrigation area that is originally composed of colonial lands devoted to viticulture and arboriculture.The Mitidja Plain is considered as one of the most fertile areas of Algeria and of the entire world due to its agricultural production.Water consumption in the agricultural sector of the plain represents almost 70% of the total volume of mobilized water,which is a considerable volume of water at current situation of water resources (Meddi and Eslamian, 2020), as in other regions of the world.This situation is prompting decision-makers to find more economical techniques to cope with climate change and the overexploitation of groundwater.In order to develop innovative techniques and approaches, it is essential to study the evolution of infiltration into the ground in order to set up intelligent control and irrigation systems.Understanding of infiltration in agricultural soils is an important phase in the design, evaluation,and management of furrow irrigation (Esfandiari and Maheshwari, 1997).

2 Materials and methods

2.1 Study area

The Mitidja Plain is located in the north of Algeria, facing the Mediterranean Sea in the northeast(36°22′30″-36°48′58″N, 02°32′07″-03°28′14″E; 300 m a.s.l.).It is one of the main agricultural plains in the Mediterranean Basin.It has a total area of nearly 1700 km2with agricultural areas ranging from 120×103to 130×103hm2.It extends from the Wadi Nador in the west, bordered by the Dahra Mountains, east of the Oued Boudouaou, from the foothills of the Atlas Blidéen to the Sahel Mountains in the south, and the Bouzaréah Massif in the north (Bouziane et al., 2021).Administratively, it includes four cities: Algiers, Blida, Boumerdes, and Tipaza.A Mediterranean climate prevails over the Mitidja Plain.Summers are hot and dry, and winters are rainy.The average winter temperature is 6°C, the average summer temperature is 33°C, and the average annual precipitation is 500-700 mm.The wet season is from October to May and the dry season is from June to September, and the estimated potential evapotranspiration in western and eastern Mitidja is about 1326 and 1271 mm, respectively (Boufekane et al., 2020).The hydrology of the study area is characterized by intense channel densities of four major rivers: Wadi Legaia, Wadi Hamiz, Wadi El Harrach in eastern Mitidja, and Wadi Mazafran in western Mitidja.The tributaries of these rivers originate from the Blidean Atlas and have considerable north-south flow.Figure 1 shows the experimental sites and soil texture.This area is characterized by fine and fertile soil.The most common soil texture is clay, and soils are dominated by alluvial and colluvial soils.Most farms are on alluvial soil.

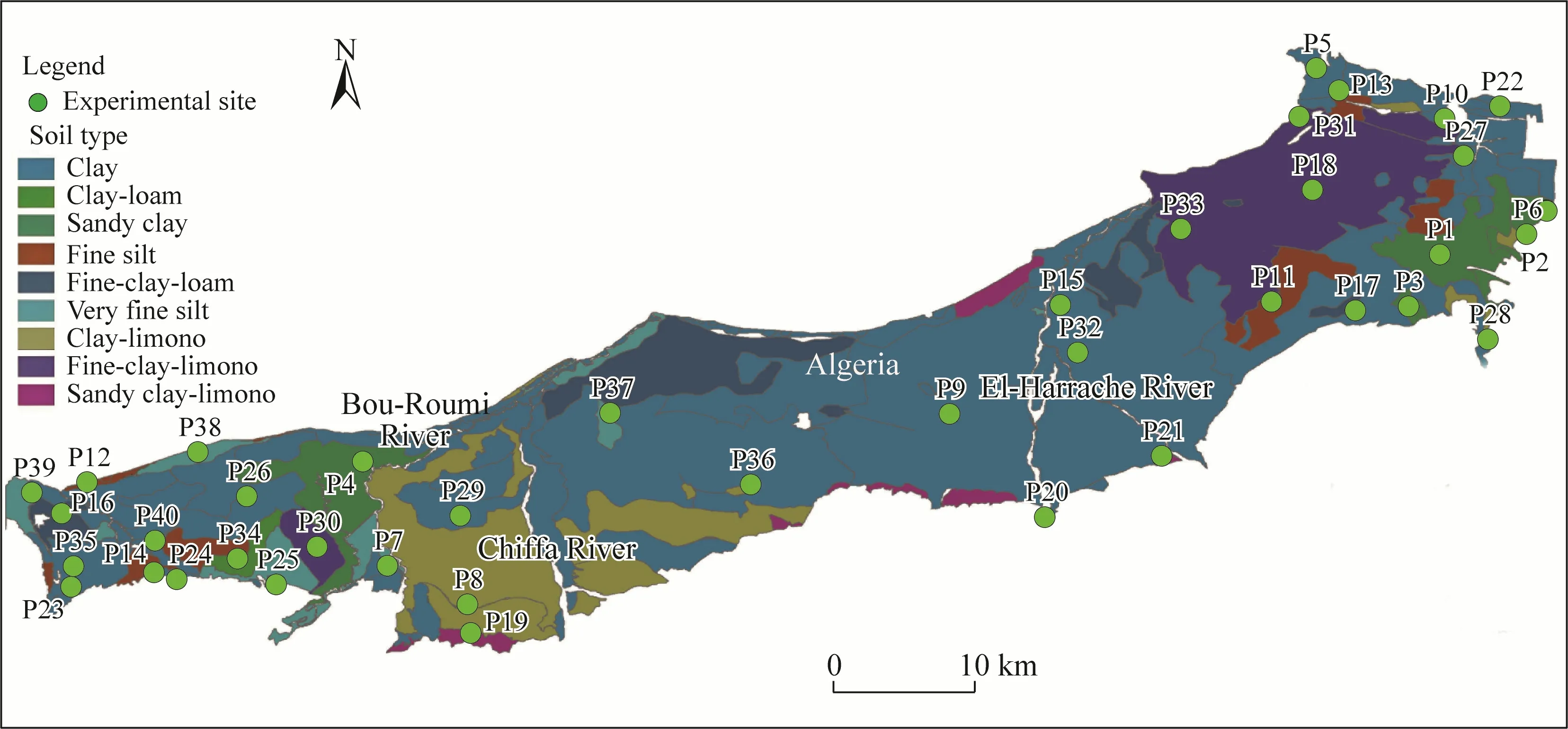
Fig.1 Study area with selected sites and soil texture (Boufekane et al., 2021; Bouziane et al., 2021)

2.2 Measurement of infiltration rate

To measure the infiltration rate, we used a double ring infiltrometer.The double ring infiltrometer is a device used to measure the infiltration rate of water into soil.It consists of two concentric rings 250 mm deep, the inner ring (110 mm) being smaller than the outer ring (320 mm), with the space between the two rings creating a circular trench (Fig.2).The rings are made of metal and are driven into the soil to 40 mm depth, leaving only the top edge of the rings exposed, both rings were filled with water to the equal depth, and the initial reading of the water level was noted.The depth of water in the inner ring of infiltrometer was noted at regular time intervals (1 min) until the rate of infiltration became steady.The infiltration rate is typically calculated as the volume of water that infiltrates into the soil per unit of time and surface area of the soil.The double ring infiltrometer is a useful tool for assessing the infiltration capacity of soil and can be used to evaluate the effectiveness of soil conservation measures, irrigation practices, and other land management practices (Soil Science Equipment | Double Ring Infiltrometer Surface Measure, 2020).It is particularly useful in agricultural area where efficient water use is important.

2.3 Experimental data

Soil samples were collected with core samplers to an average depth of 50 cm, and disturbed soil samples (40 points) were collected in the field at the site and air-dried, crushed, and passed through a 2-mm sieve to obtain soil fractions for soil texture determination.We used a textural classification triangle to classify the soil based on the results obtained from the analysis.Experimental tests were conducted individually for 40 sites (experimental samples; Fig.1).The result of analysis of soil physical properties and infiltration rate (initial and final) of the study area at each site is presented in Table 1.The results showed that the texture of sampled sites was predominantly clayey.The initial infiltration rate varies from 11.70 to 330.00 mm/h and the range of final infiltration rates was from 3.71 to 138.42 mm/h.Variations in infiltration rates are favored by the importance of root system and animals digging into the soil, insufficient pre-wetting, and soil disturbance by double rings infiltrometer.

Fig.2 Double ring infiltrometer

2.4 Infiltration models and parameters

In this study, infiltration data were fitted to the infiltration models of Kostiakov, Philip, Horton,modified Kostiakov, and Novel.

2.4.1 Kostiakov model

Kostiakov model is commonly used in irrigation engineering and is derived using data observed in the field or in the laboratory (Parhi et al., 2007).Kostiakov (1932) proposed the following best-fit infiltration equation:

wheref(t) is the infiltration rate (mm/h);ais the coefficient;tis the time (h); andbis the exponent.Both the parameters rely on soil type, initial moisture content, rainfall rate, and vegetative cover, and these can be determined empirically.

2.4.2 Modified Kostiakov model

Modified Kostiakov equation includes the term steady infiltration capacity (fc; mm/h).The parameterfcis included because the infiltration rate decreases as more water penetrates the soil,eventually reaching a constant or final infiltration rate (Vand et al., 2018).The modified Kostiakov equation is expressed as follows:

2.4.3 Philip model

Philip and De Vries (1957) proposed a model based on a semi-analytical solution of the Richards flow equation (Richards, 1931).In this solution, Philip and De Vries (1957) used a time series to solve the Richards equation.Neglecting the higher order terms, we derived the results of a two-term infiltration equation in which both parameters have physical meanings (Zakwan et al.,2016).

whereSis the Sorptivity parameter that is the function of soil matrix forces (mm/h-0.5); andKis the soil parameter related to transmission of water through soil or gravity force.

2.4.4 Horton model

Horton equation is one of the most popular empirical models simulating water infiltration into soils (Dahak et al., 2022).Infiltration equation is a three-parameter equation that is expressed as follows:

wheref0is the initial infiltration rate (mm/h);fcis the final infiltration rate (mm/h); e is the mathematical constant; andkis the rate constant in the dimension of timet(1/t).

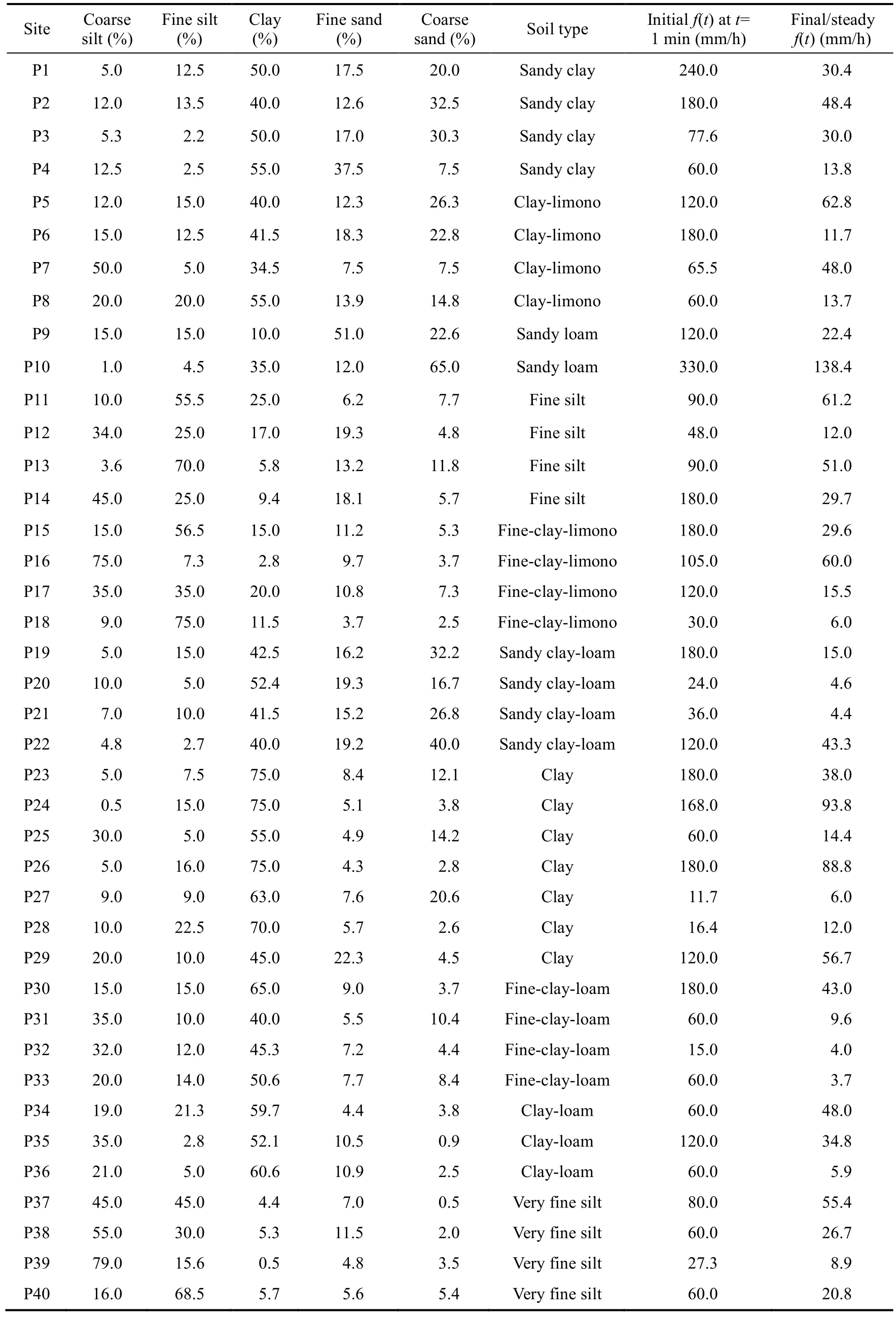
Table 1 Details of the initial and final infiltration rates (f(t)), and soil properties of the study area

2.4.5 Novel model

A typical non-linear regression model developed from the modified Kostiakov model (Sihag et al., 2017) was adopted, as shown below:

wherecis the coefficient.

2.5 Performance evaluation parameters

2.5.1 RMSE

RMSE is one of the most commonly used measures of prediction quality.It shows how far the predictions deviate from actual measured values (Bennett et al., 2013).RMSE is a good measure of accuracy, but only for comparing the prediction errors of different models or model configurations for a particular variable, not between variables.

whereaiis the simulated value;biis the observed values of infiltration rate; andnis the number of observations.

2.5.2 NSE

NSE criterion of Nash and Sutcliffe (1970) was introduced as a measure of model performance.NSE criterion better reflects the desirable and undesirable properties of model of interest and increases as the quality of model improves.NSE can be defined as follows:

wherebthe average of observations values.For nonlinear models, NSE can be negative.In

fact, it ranges from -∞ to 1.As usual (Zeybek, 2018), researchers look for NSE values close to 1.Negative values indicate unacceptable model performance.This is one of the recommended model performance metrics in hydrology as well as many other applications.

2.5.3 KGE

KGE fills several gaps in NSE and is increasingly used for model calibration and evaluation.

whereris the linear correlation coefficient between observed and computed values;Bis the ratio between SD of simulated flows and SD of observed flows; andCis the ratio between mean simulated flow and mean observed flow (Knoben et al., 2019).This coefficient is more accurate than NSE.

2.5.4 CC

CC is a statistical measure that calculates the strength of relationship between movements of two variables (Lei et al., 2020).CC is calculated as follows:

2.5.5 NRMSE

NRMSE makes it easy to compare models at different scales.NRMSE refers to RMSE of observed range of variables (Tadj et al., 2014).Therefore, NRMSE can be interpreted as part of the total range normally resolved by the model.

2.5.6 Percent bias (PBIAS)

PBIAS measures the average tendency of simulated values to be larger or smaller than observed values (Golmohammadi et al., 2014).

3 Results

3.1 Model parameters

To estimate infiltration rates in our study area, we opted for the models of the Novel, Kostiakov,modified Kostiakov, Philip and Horton.Observed field data on infiltration rates were used to evaluate these models, and numerical values for the infiltration equations parameters were obtained.The obtained model parameters and statistical parameters were done using the Rtop package of R statistical software.

A comparative analysis of soil water-infiltration characteristics for ten different classes of soil was performed.The estimated parameter values for the five selected infiltration models are listed in Table 2.The values ofbifor the Novel, Kostiakov, and modified Kostiakov infiltration models were of significant similarity across the ten soil types.In contrast, parametersfcwere completely different in the Novel, Horton, and modified Kostiakov models due to other parameters such ascin the Novel model andkin the Horton model.These empirical parameters have a soil physical meaning.A size comparison of each of the model parameters indicated that there is no relationship between the parameterkin the Horton model and Philip model.The parameteraiin the modified Kostiakov model is similar to that in the Novel model.However, this is not the case in the Kostiakov model.

Individual infiltration curves were generated from experimental tests.Results of the field infiltration rates and simulated infiltration rates for the five models for each soil class are presented in Figure 3.The graphics showed that the observed infiltration data took 35 min to 3 h to reach the steady infiltration rate.

The Philip model had the highest deviations because it overestimated the data measured at sampling points P1 and P15.The Horton model had the second lowest performance after the Philip model.This may be due to the fact that their parameters do not have a consistent physical interpretation and that the process involved in evaluating the parameters can be very sensitive to approximation errors.

For clay-sandy, fine-clay-loam, clay-loam, and clay soils, the Horton and Philip models deviated from the observed data, while the modified Kostiakov and Novel models provided a better fit.For fine-silty and very fine-silty soils, it was difficult to decide which model gave the best performance, so the performance parameters were used to make a better comparison.However, the infiltration rate estimated by the Novel model was the most effective in predicting the fit of the experimental data measured at all sampling points.

3.2 Performance parameters

Statistical criteria such as RMSE, NRMSE, CC, NSE, and KGE were used to evaluate infiltration models.We selected the best model based on the following criteria: the maximum CC, the minimum RMSE, the minimum NRMSE, the maximum NSE, and the maximum KGE.The results shown in the box plot (Fig.4) were computed for different models and the values are shown in Table 3.

The KGE and NSE values were close to 1.00, with intervals of 0.90-0.99 and 0.80-0.98,respectively, for the Horton model in sandy clay, clay-loam, and sandy loam soils.This indicatesthat the Horton model can predict the infiltration rate for these soil classes.For the remaining soil classes, the Novel model had the highest values, between 0.85 and 0.99, for both parameters.

The NRMSE values for the Philip model were unacceptable, ranging from 0.03 to 0.35.In contrast, the Novel model had the best results, with NRMSE values ranging from 0.01 to 0.19.The Kostiakov and modified Kostiakov models produced good results compared with the Philip model, with the KGE and NSE values ranging from 0.57 to 0.99 and 0.15 to 0.99, respectively,for both models.The NRMSE values for the Kostiakov and modified Kostiakov models ranged from 0.03 to 0.43 and 0.02 to 0.19, respectively.

The KGE parameter in Figure 4a showed that the Novel and modified Kostiakov models had the median value closest to the ideal value of 1.00, with a range of 0.91-0.99 and five outliers for both models.In contrast, the Philip model had the largest value ranging from 0.84 to 0.93, with three outliers.The Horton model had a uniform distribution ranging from 0.91 to 0.99, with two outliers.

For the NSE parameter in Figure 4b, the modified Kostiakov and Novel models gave the same results, with a range of 0.85-0.98 and five outliers.The Kostiakov model had the largest value ranging from 0.75 to 0.97, with only one outlier.Like the KGE parameter, the Horton model had a uniform distribution ranging from 0.83 to 0.97, with two outliers.Finally, for the NRMSE parameter in Figure 4d, the Novel and modified Kostiakov models gave the best results compared with the other infiltration models, approaching the ideal value of 0.00 with a range of 0.02-0.14.The Philip model had the highest uncertainty, with a range of 0.06-0.16, followed by the Kostiakov model (0.05-0.12) and the Horton model (0.05-0.12), in terms of estimating infiltration rate values.The Novel and modified Kostiakov models performed the best in terms of all three statistical criteria (KGE, NSE, and NRMSE) and the Philip model performed the worst.

The Novel model explained almost all the variability in the data, as indicated by its high KGE and NSE values and low NRMSE value.A comparison of the statistical parameters shows that the Novel model fits well with the measured data for all types of soil except sandy clay, clay-loam,and sandy loam soils, where the Horton model performed better.

Figure 5 showed the PBIAS errors for different infiltration models.The Novel and modified Kostiakov models had the lowest PBIAS errors, ranging from -12% to 12%, with most of the values concentrated around 0%.The Philip model had the largest PBIAS errors, ranging from-20% to 20%, with a significant number of values concentrated around 5%.The Kostiakov model had an asymmetric PBIAS distribution, ranging from -27% to 15%, similar to the Horton model(-15%-20%).Therefore, we can conclude that the Novel model has the best fit to the measured data, as it is the closest to the ideal value of 0% for PBIAS error.This is likely because the Novel model is developed from the modified Kostiakov model.The Novel model outperformed the other infiltration models in terms of statistical criteria and PBIAS error.It is therefore the most suitable model for predicting infiltration rates for a variety of soil types.This means that the Novel model explained almost all the variability in the data.A comparison of the statistical parameters shows that the Novel model fits well with the measured data.The Novel model gave the best fit to the measured infiltration rate for all types of soil except for sandy clay, clay-limono, and sandy loam soils.

Figure 5 showed that the Novel and modified Kostiakov models gave better results because they had the least errors such that the PBIAS was between -12% and 12%, and had the most density 0%,whereas the Philip model had a large variation ranging from -20% to 20% with an important density around 5%.The Kostiakov model had asymmetric PBIAS plot ranging from -27% to 15%,and Horton model from -15% to 20%.So, we can conclude that the Novel model has the best fit in view of the fact that the Novel model is developed from the modified Kostiakov model.

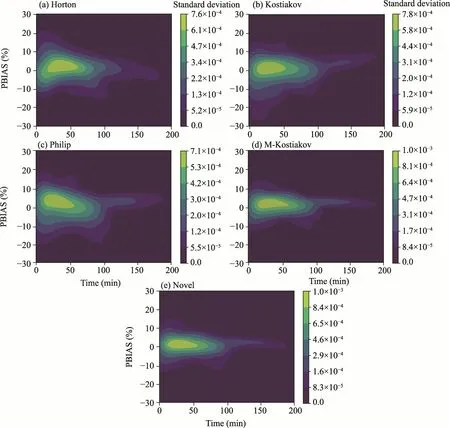
Fig.5 Distribution of PBIAS (percent bias) of different infiltration models.(a), Horton model; (b), Kostiakov model; (c), Philip model; (d), M-Kostiakov (modified Kostiakov) model; (e), Novel model.

4 Discussion

In the context of our current research, we applied infiltration models across ten distinct soil types with the primary aim of evaluating the performance of five infiltration models when compared with observed data.This comprehensive analysis allowed us to gain valuable insights into the effectiveness of these models in accurately predicting infiltration characteristics in a diverse range of soils.The results of our study, which are presented in Table 3, and Figures 4 and 5,demonstrated the superiority of the Novel model in replicating observed experimental data.This model demonstrated remarkable success in forecasting infiltration behavior in seven different soil types, with exceptional accuracy.It is important to note that, while the Novel model excelled for the majority of soil types, three exceptions were identified, namely sandy clay, clay-limono, and sandy loam soils, which were best characterized by the Horton model.This finding aligns with the results of Singh et al.(2018), who predicted cumulative infiltration rate under inceptisols in tropical dry brown soils and found the Novel and modified Kostiakov models to be more suitable than the Kostiakov and SCS (soil conservation service) models.Furthermore, our assessment encompassed a broader scope, extending to the region of Lafia in North Central Nigeria, where four distinct infiltration models were evaluated, namely the Kostiakov, modified Kostiakov,Philip, and Horton.In this specific context, the Horton model emerged as the most suitable fit for measured cumulative infiltration rate, as affirmed by Ogbe et al.(2011).This particular finding holds significance for the practical application of infiltration modeling in that region.Additionally,Wang et al.(2017) concluded that the Mezencev and Horton models offer a more accurate description of the relationship between cumulative infiltration and infiltration time when biochar is introduced into the soil.Moreover, as deduced by Duan et al.(2010), the Mezencev and the Horton models surpassed the other three infiltration models in terms of performance.Their researches provided the most accurate depiction of the intricate relationship between cumulative infiltration and infiltration time within the lawn soils.This finding underscores the superior capabilities of the Mezencev and Horton models, shedding light on their ability to offer a more precise representation of infiltration rate.

It should be noted that the result of Duan et al.(2010) closely mirrors our findings for sandy clay, clay-limono, and sandy loam soils, where the Horton model exhibited a superior fit when compared with the Novel model.This intriguing consistency in results further gains support from parallel experiments conducted at the Agricultural Research Farm of the Bahauddin Zakariya University in Multan, Pakistan, as detailed by Farid et al.(2019).Their research involved the assessment of three distinct infiltration models, namely the Kostiakov, Philip, and Horton models.Their results reinforce the effectiveness of the Horton model in accurately describing infiltration behavior.Moreover, Rasool et al.(2021) found that the modified Kostiakov model consistently outperforms other models in terms of infiltration predictions.Our study also confirmed its modeling power except for the Horton model.These results underscore the necessity of thoroughly assessing and documenting the performance of various infiltration models at specific locations.Haghighi et al.(2010) emphasized the importance of evaluating each model's ability to estimate final infiltration rates at different geographic sites.Such location-specific evaluation are essential in modeling infiltration to meet the unique requirements of individual regions.Indeed,the applicability of infiltration models is not universal, as conducted by Machiwal et al.(2006)and Oku and Aiyelari (2011).Their work affirms that one or more infiltration models may be better suited for a particular location, further reinforcing the idea that not all models are universally suitable for all soil types and geographic settings.

The Novel model serves as a valuable tool for generating infiltration data specifically tailored to the soils within the Mitidja Plain.The insights gained from this work contribute to the broader goal of enhancing water resource management in the Mitidja Plain.The enhanced modeling provided by this research offers a more comprehensive understanding of water flow dynamics,which is vital for safeguarding the region against flooding and ensuring the efficient use of water resources.In summary, the Novel model's capacity to generate infiltration data tailored to the Mitidja Plain's soils has far-reaching implications.

5 Conclusions

Infiltration models have become one of the most important tools for managing water resource.In this work, an attempt was made to validate the predictive accuracy of five infiltration models using measurements from a double ring infiltrometer.A comparison of field and predicted infiltration rates showed that the Novel model-predicted infiltration rates were much closer to the observed data.The NRMSE and KGE results show that the infiltration rate can be predicted by the Novel, modified Kostiakov, Horton, Kostiakov, and Philip models.Based on the mean NRMSE values, we concluded that the Novel model provided the lowest values, and that the infiltration was adequately described by this model.As shown by the results, the Novel model had the lowest PBIAS in predicting infiltration rates.Thus, in the absence of measured infiltration data, the Novel model can be used to generate infiltration information for the Mitidja Plain and the other plains in northern Algeria and North Africa.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was conducted by the Water and Environment Engineering Laboratory (GEE) of the Higher National School of Hydraulics (ENSH), and this study is carried out within the framework of the SWATCH project (Prima project) funded by the DGRSDT, Algeria.

Author contributions

Conceptualization: Amina MAZIGHI, Mohamed MEDDI; Methodology: Amina MAZIGHI, Mohamed MEDDI,Giovanni RAVAZZANI, Mouna FEKI; Formal analysis: Amina MAZIGHI, Mohamed MEDDI, Ishak ABDI;Writing - original draft preparation: Amina MAZIGHI, Mohamed MEDDI, Hind MEDDI; Writing - review and editing: Amina MAZIGHI, Hind MEDDI; Funding acquisition: Mohamed MEDDI, Hind MEDDI; Resources:Amina MAZIGHI, Mohamed MEDDI, Giovanni RAVAZZANI, Mouna FEKI, Ishak ABDI, Hind MEDDI;Supervision: Mohamed MEDDI, Hind MEDDI.