羅永亮,楊 海,陳江濤

(西安工程大學(xué)理學(xué)院,陜西 西安 710048)

1 引言及結(jié)論

設(shè)Z,N*分別表示全體整數(shù)和正整數(shù)的集合,且a,b是大于1的正整數(shù),近些年來(lái),討論方程

(an-1)(bn-1)=x2,x,n∈N*,

(1)

的正整數(shù)解問(wèn)題成為數(shù)論中的一個(gè)引人注目的重要課題.對(duì)此,COHN J H E[1]證明了:當(dāng)(a,b)=(2,3),(2,6)時(shí),方程(1)無(wú)解.同時(shí),HAJDUL[2],SZALAY L[3]還對(duì)b=ak,對(duì)于其中k是大于1的正整數(shù)情況,給出了方程(1)正整數(shù)解的相關(guān)結(jié)論.另外,賀光榮[4]還討論了更一般的方程

(an-1)(bn-1)=x2,x,m,n∈N*,

(2)

證明了當(dāng)(a,b)=(2,3)時(shí),方程(2)無(wú)正整數(shù)解.近些年來(lái)諸多學(xué)者如梁明[5],付瑞琴[6],楊海[7]和Refik Kidskin[8]研究此類及相關(guān)的指數(shù)丟番圖方程,得出了許多很有價(jià)值的結(jié)論,積極推動(dòng)這一類型方程的解決.此外,潘承洞,潘承彪[9]在初等數(shù)論一書中嚴(yán)謹(jǐn)系統(tǒng)地給出了初等數(shù)論的基本方法和經(jīng)典結(jié)論,為解決丟番圖方程問(wèn)題提供了理論基礎(chǔ).

唐波,楊仕春[10]研究了方程((10k1+2)n-1)((10k2+3)n-1)=x2,k1,k2∈N*的正整數(shù)解,并給出方程無(wú)正整數(shù)解時(shí)的情況.

樂(lè)茂華[11],曹珍富[12],華羅庚[13]等分別介紹了在不同條件下指數(shù)丟番圖方程的正整數(shù)解的問(wèn)題,并給出了研究此類問(wèn)題的一些方法和結(jié)論.

楊仕椿,吳文權(quán)[14]給出了方程((13k1+5)n-1)((13k2+8)n-1)=x2,k1,k2∈N*與((17k1+6)n-1)((17k2+7)n-1)=x2,k1,k2∈N*解的一些相關(guān)的結(jié)論.

樂(lè)茂華[15]證明了方程(2n-1)((6k)n-1)=x2,k,n,x∈N*沒(méi)有正整數(shù)解(n,x).

由于方程(1)在研究某類特定的指數(shù)方程以及在代數(shù)學(xué)中的群論以及密碼學(xué)等領(lǐng)域中有較為深刻的應(yīng)用,因此研究a,b取較大正整數(shù)時(shí),方程(1)的解的情況是非常有必要的.

本文將研究指數(shù)丟番圖方程

((mk1+m1)n-1)((mk2+m2)n-1)=x2,x,n∈N*,

(3)

其中

m,m1,m2,p,k1,k2,x,n∈N*;以及方程

((mk1+m1)n-1)((mk2+m2)n-1)=x2,x,n∈N*,

(4)

其中

m,m1,m2,p,k1,k2,x,n∈N*.在研究過(guò)程中,主要運(yùn)用二次剩余的初等方法和已被證明的經(jīng)典結(jié)論,給出了關(guān)于這兩個(gè)方程在特定條件下解的情況.

定理1.1 設(shè)m1+m2≡0(modm),當(dāng)n≡0,1,3(mod4)時(shí),方程(3)和(4)均沒(méi)有正整數(shù)解(n,x).

定理1.2 設(shè)m1+m2=(8q-7)m,q∈N*,當(dāng)

(i)k1≡0,2(mod8),k2≡0(mod2);

(ii)k1≡1(mod2),k2≡5,7(mod8);

以上兩個(gè)條件任意一個(gè)成立時(shí),則方程(3)沒(méi)有正整數(shù)解(n,x).

定理1.3 設(shè)m1+m2=(8q-7)m,q∈N*,當(dāng)

(i)k1≡4,6(mod8),k2≡0(mod2);

(ii)k1≡1(mod2),k2≡5,7(mod8);

以上兩個(gè)條件任意一個(gè)成立時(shí),則方程(4)沒(méi)有正整數(shù)解(n,x).

符號(hào)說(shuō)明:對(duì)任意的素?cái)?shù)p,pa‖n表示pa恰好整除n,而pa+1不整除n;讀作pa恰整除n.

2 引理

引理2.1[13]若4|n,則方程(1)僅在(a,b)=(13,239)時(shí)有解,而且僅有解(n,x)=(4,9 653 280).

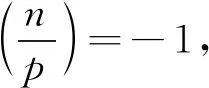
引理2.3 若k,A均為奇數(shù),則方程2kA=x2沒(méi)有正整數(shù)解.

證明:由k,A均為奇數(shù),則2kA質(zhì)因數(shù)分解中的2的次冪為奇數(shù)k,因?yàn)閤2質(zhì)因數(shù)分解中的2的次冪必為偶數(shù),所以方程2kA=x2沒(méi)有正整數(shù)解.

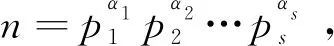
引理2.5[9]設(shè)p為質(zhì)數(shù),Legendre符號(hào)具有以下性質(zhì):

引理2.6[9]設(shè)p為質(zhì)數(shù),Jacobi符號(hào)具有以下性質(zhì):

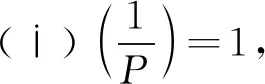
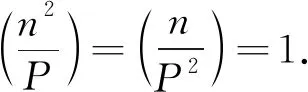
引理2.7[9]設(shè)P>1的奇數(shù),則有

3 定理證明

定理1.1的證明

根據(jù)引理1.1,假設(shè)方程(3)和(4)在n=0(mod 4)時(shí),存在(a,b)=(13,239),則

a+b=239+13=22×32×7≡0(modm),

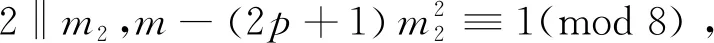
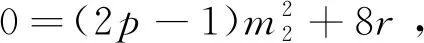
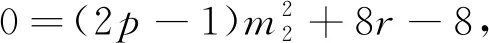
當(dāng)m=21時(shí),可得21k1+m1=13或21k2+m2=13,因?yàn)閗1,k2,m1,m2均為正整數(shù),等式不成立.

故方程(3)和(4)在n=0(mod 4)條件下,沒(méi)有正整數(shù)解(n,x).

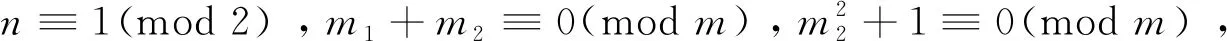
因?yàn)?/p>

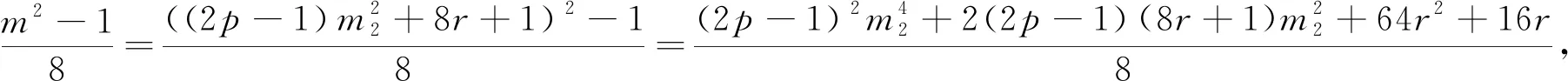
定理1.2的證明

S=((mk1+m1)n-1)((mk2+m2)n-1)=

((mk1+m1)2-1)((mk1+m1)2(w-1)+(mk1+m1)2(w-2)+…+1)((mk2+m2)n-1).

令A(yù)=((mk1+m1)2(w-1)+(mk1+m1)2(w-2)+…+1)((mk2+m2)n-1),則A為奇數(shù).

當(dāng)k1≡0(mod 8)時(shí),設(shè)k1=8t,則

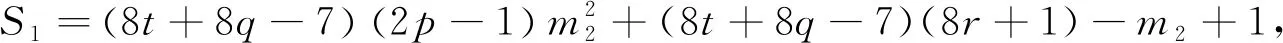
由m2≡2(mod 8),得4‖S1,2‖S2,進(jìn)而可以得到8‖(mk1+m1)2-1,故23‖S,由引理2.3可知方程(3)無(wú)正整數(shù)解(n,x).

當(dāng)k1≡2(mod 8)時(shí),設(shè)k1=8t+2,則

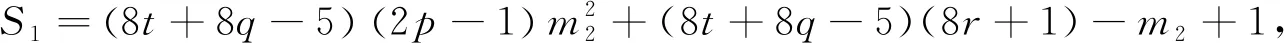
由m2≡2(mod 8),得4‖S2,2‖S1,進(jìn)而可以得到8‖(mk1+m1)2-1,故23‖S,由引理2.3可知方程(3)無(wú)正整數(shù)解(n,x).綜上以上兩種情況,即得方程(3)滿足條件(i)時(shí),無(wú)正整數(shù)解(n,x).

S=((mk1+m1)n-1)((mk2+m2)n-1)

=((mk2+m2)2-1)((mk2+m2)2(w-1)+(mk2+m2)2(w-2)+…+1)((mk1+m1)n-1).

設(shè)A=((mk2+m2)2(w-1)+(mk2+m2)2(w-2)+…+1)((mk1+m1)n-1),則A為奇數(shù).

當(dāng)k2≡5(mod 8),設(shè)k2=8t+5,則

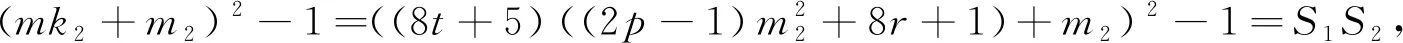
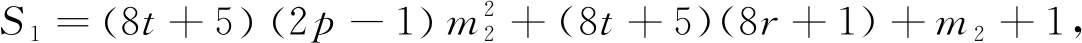
由m2≡2(mod 8),得4‖S1,2‖S2,進(jìn)而可得8‖(mk2+m2)2-1,故23‖S,由引理2.3可知方程(3)無(wú)正整數(shù)解(n,x).

當(dāng)k2≡7(mod 8),設(shè)k2=8t+7,則

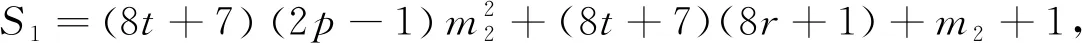
因?yàn)閙2≡2(mod 8),得2‖S1,4‖S2,進(jìn)而可得8‖(mk2+m2)2-1,故23‖S,由引理2.3可知方程(3)無(wú)正整數(shù)(n,x).綜合以上兩種情況,即得方程(3)滿足條件(ii)時(shí),無(wú)正整數(shù)解(n,x).故方程(3)滿足條件(ⅰ) (ⅱ) 任意一種情況時(shí),無(wú)正整數(shù)解(n,x).定理1.2證畢.

定理1.3的證明

S=((mk1+m1)n-1)((mk2+m2)n-1)=

((mk1+m1)2-1)((mk1+m1)2(w-1)+(mk1+m1)2(w-2)+…+1)((mk2+m2)n-1).

令A(yù)=((mk1+m1)2(w-1)+(mk1+m1)2(w-2)+…+1)((mk2+m2)n-1),則A為奇數(shù).

當(dāng)k1≡4(mod 8)時(shí),設(shè)k1=8t+4,則

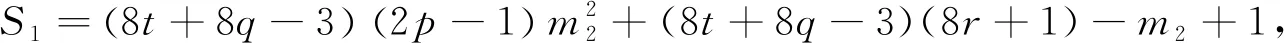
由m2≡6(mod 8),得4‖S1,2‖S2,進(jìn)而可以得到8‖(mk1+m1)2-1,故23‖S,由引理2.3可知方程(4)無(wú)正整數(shù)解(n,x).綜上以上兩種情況,即得方程(4)滿足條件(i)時(shí),無(wú)正整數(shù)解(n,x).

當(dāng)k1≡6(mod 8)時(shí),設(shè)k1=8t+6,則

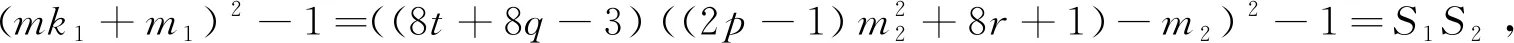
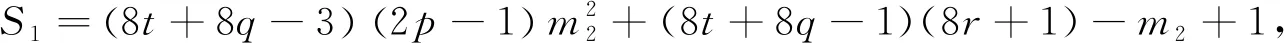
由m2≡6(mod 8),得2‖S1,4‖S2,進(jìn)而可以得到8‖(mk1+m1)2-1,故23‖S,由引理2.3可知方程(4)無(wú)正整數(shù)解(n,x).綜上以上兩種情況,即得方程(4)滿足條件(i)時(shí),無(wú)正整數(shù)解(n,x).

S=((mk1+m1)n-1)((mk2+m2)n-1) =

((mk2+m2)2-1)((mk2+m2)2(w-1)+(mk2+m2)2(w-2)+…+1)((mk1+m1)n-1).

令A(yù)=((mk2+m2)2(w-1)+(mk2+m2)2(w-2)+…+1)((mk1+m1)n-1),則A為奇數(shù).

當(dāng)k2≡1(mod 8),設(shè)k2=8t+1,則

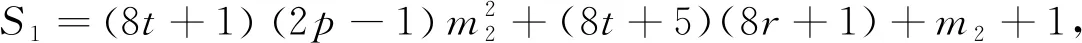
由m2≡6(mod 8),得4‖S1,2‖S2,進(jìn)而可得8‖(mk2+m2)2-1,故23‖S,由引理2.3可知方程(4)無(wú)正整數(shù)解(n,x).綜合以上兩種情況,即得方程(4)滿足條件(ii)時(shí),無(wú)正整數(shù)解(n,x).

當(dāng)k2≡3(mod 8),設(shè)k2=8t+3,則

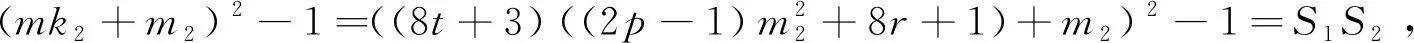
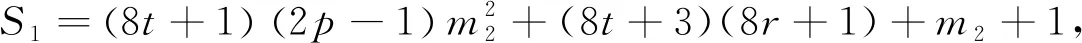
由m2≡6(mod 8),得2‖S1,4‖S2,進(jìn)而可得8‖(mk2+m2)2-1,故23‖S,由引理3可知方程(4)無(wú)正整數(shù)解(n,x).綜合以上兩種情況,即得方程(4)滿足條件(ii)時(shí),無(wú)正整數(shù)解(n,x).

故方程(4)滿足條件(ⅰ) (ⅱ)任意一種情況時(shí),無(wú)正整數(shù)解(n,x).定理1.3證畢.

4 結(jié)論

關(guān)于方程(an-1)(bn-1)=x2,x,n∈N*可解性的探究還遠(yuǎn)未完成,眾多學(xué)者在限定a,b參數(shù)情況下,討論了這一類型方程的正整數(shù)解,得到了很多具有價(jià)值的結(jié)果;顯然根據(jù)文中三個(gè)定理,可以探究出無(wú)窮多組該方程無(wú)正整數(shù)的情況,為推動(dòng)解決此類丟番圖方程的問(wèn)題提供一定思路和方法.