Valley-dependent transport in a mescoscopic twisted bilayer graphene device
Wen-Xuan Shi(史文萱), Han-Lin Liu(劉翰林), and Jun Wang(汪軍)
School of Physics,Southeast University,Nanjing 210096,China
Keywords: twisted bilayer graphene,valley-dependent transport,graphene nanoribbon,conductance
1.Introduction
Over the past decade, there has been extensive and intensive research on twisted bilayer graphene (TBG) due to its fascinating properties, leading to the emergence of a new discipline called twistronics in similar van der Waals heterostructures of two-dimensional materials by controlling the relative twist angle between the two monolayers.[1–17]Near the so-called magic angle of TBG, a wide range of correlated physics has been experimentally observed, including Mott insulator,[18]superconductivity,[7,8]ferromagnetism,[19]and topology.[20–25]These exotic behaviors are closely related to the flat bands near the charge neutrality point arising from the large-scale moir′e pattern.The system’s properties are quite sensitive to electronic correlations and interactions when the band width is extremely narrow and the electron velocity is almost vanishing.For large twist angles, the low-energy behavior of TBG matches that of monolayer graphene, and the coherent interlayer transport is suppressed.[26,27]
Several studies[28–34]have focused on directly investigating the electronic transport of TBG using the tight-binding lattice model with arbitrary twist angles.This is because transport properties closely follow the band structure of the system and can be directly measured in experiments.Olyaeiet al.[28]calculated the conductance of a mesoscopic TBG coupled with monolayer graphene leads and identified three qualitatively different twist angle regions: large (θ10°), intermediate(3°–10°),and small(1°–3°)angle cases,in which the transport properties behave differently.Bahamonet al.[29]discovered emergent magnetic textures in a current-driven TBG system using the same numerical method when the twist angle is around the magic angle(θ~1.05°).
In TBG, the moir′e pattern can lead to the alternation of the AB and BA stackings as well as the regrouping effect of the band structure compared with the monolayer graphene,so the TBG can be employed to control the valley transport of electrons.Since a single moir′e pattern can contain several thousands of atoms in the low twist angle regime, Beuleet al.[32]employed a Wannier-like tight-binding model[35–37]to show that the TBG can produce valley-polarized electrons by use of the regrouping effect of the TBG band or Lifshitz transition with the help of an external gate voltage.The possible valley current splitter was also studied in Ref.[31] based on the zero-energy modes at the interface of the AB and BA stacking regions, which is induced by a perpendicular electric field.While the simplified tight-binding-parametrization model can capture most features of the low-energy band of moir′e patterns, it may lose some topology properties of the TBG band.Therefore,it is desirable to study valley-dependent electron transport in TBG directly using the original TBG lattice model,despite the large unit cells at smaller twist angles.
In this study, we investigate valley transport in a fourterminal mesoscopic device comprised of two monolayer graphene nanoribbons vertically stacked together to form a TBG intersection with a controllable twist angle.We numerically calculate both the longitudinal and transverse conductances using the original graphene lattice model in the clean limit.Our results show that both conductances exhibit clear valley polarization,which stems from the regrouping effect of the TBG band.Valley polarization occurs in the low Fermienergy regime when the twist angle is small,around the magic angle,and it shifts to the high energy regime as the twist angle increases.However,for relatively large twist angles,the valley polarization becomes weak since the two layers of TBG appear to be disconnected to match the single monolayer graphene’s property.
This work is organized as follows.In Section 2, we introduce a device model composed of the two single-layer graphene nanoribbons as well as the formulas for calculating the conductance.The numerical calculations of the valleydependent conductances among different terminals are performed in Section 3 and the results are analyzed in detail.A brief conclusion is drawn in the last section.
2.Model and formula
We get started with the four-terminal mesoscopic device schematically shown in Fig.1,where the two same monolayergraphene nanoribbons are overlapped together and the intersection is the TBG region.The ribbon edge is chosen to be the zigzag termination here, because the wavefunctions of electrons propagating in the ribbon can be conveniently divided into two separate valleys, marked as theKorK'valley.The ribbon width is set asNrepresenting the atom number of a transverse armchair chain or a unit slice, and the length of the ribbon is set asLdenoting the armchair-chain number involved in the calculations,therefore,the total atom number in the studied 4-terminal device is 2NL.The twist angle of the TBG is denoted asθ,with the twist axis located in the central region of the device at position(N/2,L/2),where one atom in the top layer overlaps exactly over another one in the bottom layer.
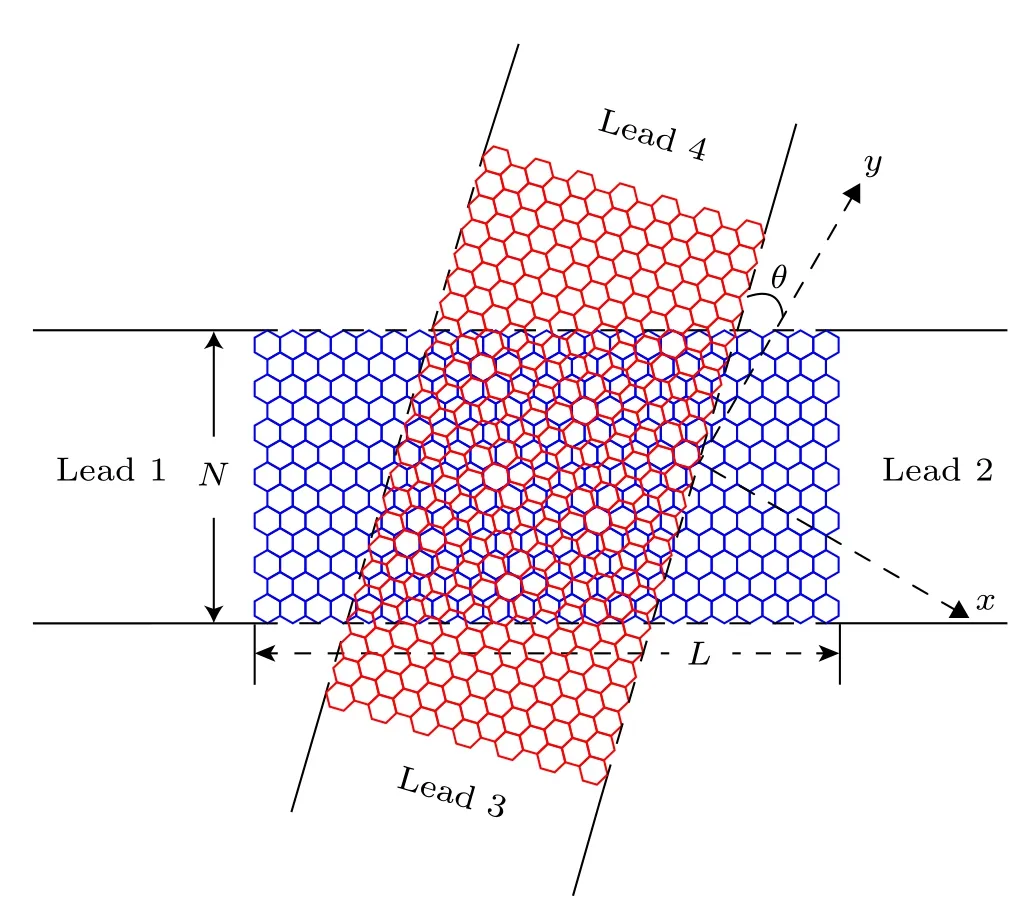
Fig.1.Schematic of a four-terminal mesoscopic device of the two graphene nanoribbons stacked together.Four leads are assumed infinitely long and each ribbon’s edge is zigzag terminated.The pristine AB stacking of the bilayer graphene is along the y-axis and θ denotes the twist angle of two layers. N and L represent the width and length of the ribbon,respectively.
A tight-binding Hamiltonian is employed to describe the device and only the pzorbit of each C atom is assumed active
where cosφi j=d0/rijwithri j=ri ?rj, and the distancedependent Slater–Koster parameters are given by

In the lattice model, the valley-dependence conductance of the four-terminal device is calculated by[40]

Despite the lack of translational symmetry in the incommensurate-structured TBG, the recursion method can still be used to calculate the Green’s functionGrthrough the tight binding model.However,it remains challenging to divide the scattering region into the same-size block or supercell/slice even for the finite-size commensurate TBG region.Nonetheless, our main concern is the correlation functionGrlm, and it is possible to group the two slices from thel-th andm-th leads into a single block inHc.The other components ofHccan be considered gradually when calculatingGrby the Dyson equation.Thus,theHccan be divided into different-size blocks in a calculation-tolerable manner.
3.Result and discussion
In our numerical calculations,we set the hopping energyt=V0ppπ=?2.7 eV as the energy unit,while the width of the ribbon isN=2048,corresponding to a width of about 220 nm with the lattice constanta0=1.44 ?A.The length of the ribbon in the device isL=N, which is approximately 380 nm.The scattering region of the device comprisesNr=2NLcarbon atoms.However,the atom number in the intersection region forming the TBG is slightly smaller thanNras shown in Fig.1,but it still contains hundreds of moir′e supercells,even for a small twist angleθ.
Prior to presenting our numerical results,it is worth noting the regrouping effect of the TBG band,which arises from the electron band in the monolayer graphene Brillouin zone folded into the much smaller moir′e Brillouin zone.Therefore, there are many new bands emergent due to reduction of Brillouin zone since the energy eigenvalues of electrons keep the same,and then the interaction between the two single layers gives rise to numerous emergent subbands and even the new band gaps, subsequently, the van Hove singularities in the density of states of the TBG appear at the edges of these subbands.[41–44]
We first present the valley-resolved longitudinal conductanceand, representing theKorK'channel conductance of lead 2 when the electrons are injected from lead 1,
The longitudinal conductance is actually the monolayer graphene nanoribbon’s one within the influence of an additional nanoribbon layer stacked above.The results are plotted in Fig.2 with three typical twist angles: the small (θ=2°),the intermediate (θ= 5°), and the large (θ= 30°) cases,which were classified in Ref.[28]to denote different transport regimes.
In Fig.2(a),the conductance profiles ofandshow an increase linearly with the Fermi energyE, and there exist some small deviations (dips) in the relative high energy region,which are the van Hove singularities due to the regrouping effect of electron bands.In other words, the two layers are loosely coupled,especially from the standpoint of the low energy regime.Besides,the valley polarization defined by the conductance difference,, is also very low.Notice thatin the clean limit even for a monolayer graphene nanoribbon case, because the lowest subband of the zigzag-edge nanoribbon is only contributed by one valley conductance due to the formation of the edge state.
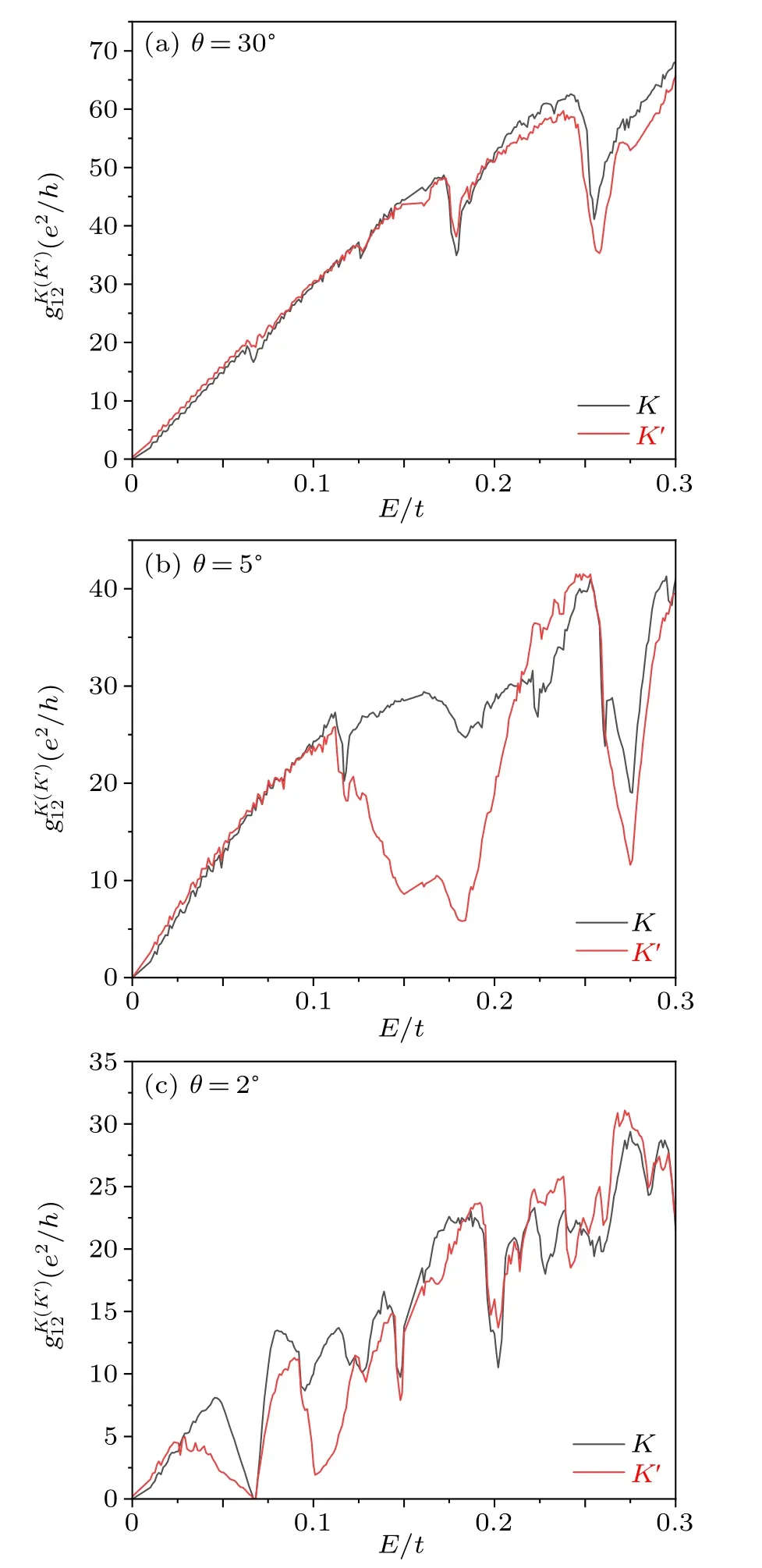
Fig.2.Longitudinal valley-dependent conductance of and as a function of the Fermi energy E for different twist angles.Parameters are marked in each panel and described in the text.
For an intermediate twist angleθ=5°,andare also depicted in Fig.2(b).It can be seen that both of them increase linearly withEfor the very low energy region but the valley polarization ofrapidly increases whenE0.12t,which is the maximum hopping energyof the two layers of the TBG,indicating where is a van Hove singularity in the TBG band.This valley polarization is much more pronounced than that in Fig.2(a), although the conductance for the large twist angleθ=30°case exhibits also a weak dip behavior.Moreover,we note that the large valley polarization shifts towards the low energy regime.Similarly,the reduction tendency ofwith decreasingθindicates a shift of the energy band of the TBG towards the low energy regime.
Whenθdecreases further, the first van Hove singularity of the TBG band seems to be pushed to the much lower energy regime,where the nearly flat band shall develop as 1°θ3°.This will result in a drastic change in the conductance landscape.Figure 2(c)shows the case forθ=2°:varies rapidly withEfor the entire energy regime.The relationship betweenandEdeviates significantly from a linear relationship, and the conductance difference between the two valley channels is clear even for very low Fermi energy.This suggests that the two layers of the TBG are tightly coupled in comparison to Figs.2(a)and 2(b).We note that there is a conductance zero atE~0.06t,which reflects an energy gap in the band structure of the TBG whenθis small.This energy gap has been observed in experimental measurements[43]aroundθ=2°.
The conductance dips in Fig.2 generally imply that there are van Hove singularities due to the regrouping effect of the electron band, so the Lifshitz transition of the band can account for the valley polarization of the conductance, which has been already employed to produce the valley polarization in the monolayer graphene or the TBG system with the help of local potentials.[32,40]For the graphene-nanoribbon leads in our device, the valley degree of freedom is well defined but in the TBG region, other bands (or energy minimum points)arise and destroy the valley definition because it is defined as the energy minimum in the momentum space,so the valley polarization of conductance implies there should be a valley Hall effect in the system.


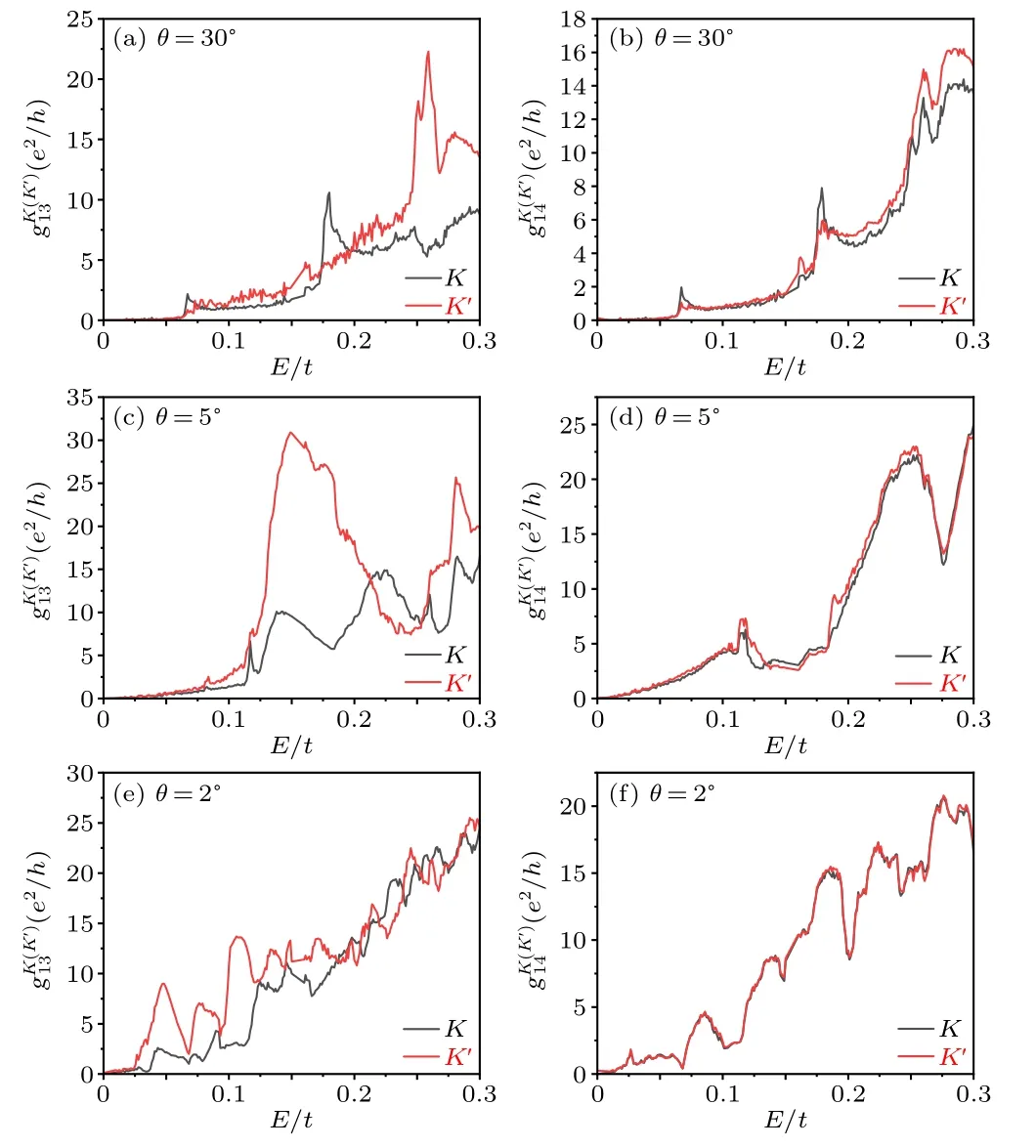
Fig.3.Transverse valley-dependent conductance of and as a function of the Fermi energy E for different twist angles.Parameters are marked in each panel and described in the text.

The conductance profiles for both transverse and longitudinal conductances exhibit rapid oscillation behaviors, owing to the presence of many bands in the small moir′e Brillouin Zone, as well as many van Hove singularities.We have only calculated several incommensurate structures withθ=30°,5°,and 2°,but the commensurate structures can display similar trends with many dips or peaks in the conductance-energy dependence.Additionally, we have not shown the conductance of the hole band (E <0) since the qualitative results remain the same as those presented in Figs.2 and 3.
4.Summary
We have investigated valley transport in a four-terminal mesoscopic device consisting of two monolayer graphene ribbons stacked together, where the intersection region is the TBG with an adjustable twist angle.We numerically calculate the valley-dependent longitudinal and transverse conductances and find that significant valley polarization occurs mainly around the conductance dip where the van Hove singularity of the band exists.As the twist angle decreases, the valley polarization becomes larger and appears in much lower energy regime.In the case of relatively large twist angles,the valley polarization is shown to be quite small since the coupling of the two layers of the TBG is weak for the low energy regime.
Acknowledgment
Project supported by the National Natural Science Foundation of China(Grant Nos.12174051 and 11874221).
- Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
- Controllable high Curie temperature through 5d transition metal atom doping in CrI3
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals

