謝子康,鄧貴新

(南寧師范大學 數(shù)學與統(tǒng)計學院,廣西 南寧 530100)

1 問題背景

本文中的圖都是有限簡單圖.圖G的頂點集和邊集分別記為V(G)和E(G),G中頂點x的點鄰域N(x)和邊鄰域E(x)分別表示關聯(lián)x的頂點的全體和關聯(lián)x的邊的全體.對正整數(shù)n≥3,用Cn表示含有n個頂點的圈,用n表示n階循環(huán)群.交換群A的指數(shù)記為exp(A).圖G1與G2的卡氏積,記作G1□G2,是以V(G1)×V(G2)為頂點集,且兩個頂點(x1,y1)與(x2,y2)相鄰當且僅當x1=x2且y1y2∈E(G2),或x1x2∈E(G1)且y1=y2.

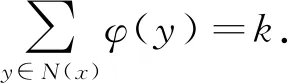
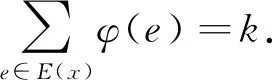
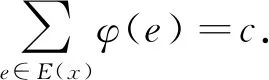
由定義1.2馬上得到,如果G是超幻圖,則G是n-超幻圖,其中n=|E(G)|.文獻[7]利用的結果證明了對任意正整數(shù)m,n≥3,Cn□Cm是2nm-超幻圖.Froncek等[8]用統(tǒng)一的構造方式重新證明了該結論.很自然地,我們考慮哪些2nm階交換群A使得Cn□Cm是A-超幻圖.本文證明了對任意正整數(shù)n≥3及任意2n2階交換群A,Cn□Cn都是A-超幻圖.

2 主要結果

引理2.1[3]設A是有限交換群,H是A的一個指數(shù)為2n的子群(n為正整數(shù)),則存在xi,yi,c∈A,xi+yi=c,0≤i≤n-1,使得

定理2.2對任意正整數(shù)n≥3和任一2n2階交換群A,Cn□Cn都是A-超幻圖.

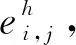
由有限交換群的結構定理可知A必有n階子群.任取A的一個n階子群H={h0,h1,…,hn-1},則由引理2.1,存在xi,yi,c∈A,xi+yi=c,0≤i≤n-1,使得

為敘述簡便,以下x,y,h的下標以及頂點(i,j)的分量都模n計算.

情形1n是偶數(shù).定義映射φ:E→A如下:

其中0≤i,j≤n-1.那么(i,j)關聯(lián)的水平邊的標號和為

而(i,j)關聯(lián)的豎直邊的標號和為

所以與 (i,j)關聯(lián)的所有邊上的標號和為

還需證明φ是雙射.對每個i,顯然有

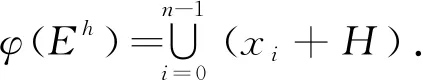
故有

這表明φ是從E=Eh∪Ev到A的滿射.又因為|E|=|A|=2n2,故φ是雙射.

情形2n是奇數(shù).定義ψ:E→A如下:

對于(i,j)∈V,其關聯(lián)的水平邊的標號和為

而(i,j)關聯(lián)的豎直邊的標號和為

從而有

還需要證明ψ是雙射.由n是奇數(shù)知,對任意r,s,存在整數(shù)i1,j1和i2,j2滿足同余式