Jinsong Tng ,Linfng Qin ,b,*,Longmio Chen ,Gungsong Chen ,Mingming Wng ,Gungzu Zhou

a Nanjing University of Science and Technology, Nanjing 210094, China

b Northwest Institute of Mechanical and Electrical Engineering, Xianyang 712099, China

Keywords:Ammunition delivery system Electromechanical coupling dynamics Uncertainty quantification Generalized probability density evolution

ABSTRACT In this paper, a dynamic modeling method of motor driven electromechanical system is presented, and the uncertainty quantification of mechanism motion is investigated based on this method.The main contribution is to propose a novel mechanism-motor coupling dynamic modeling method, in which the relationship between mechanism motion and motor rotation is established according to the geometric coordination of the system.The advantages of this include establishing intuitive coupling between the mechanism and motor, facilitating the discussion for the influence of both mechanical and electrical parameters on the mechanism,and enabling dynamic simulation with controller to take the randomness of the electric load into account.Dynamic simulation considering feedback control of ammunition delivery system is carried out, and the feasibility of the model is verified experimentally.Based on probability density evolution theory, we comprehensively discuss the effects of system parameters on mechanism motion from the perspective of uncertainty quantization.Our work can not only provide guidance for engineering design of ammunition delivery mechanism, but also provide theoretical support for modeling and uncertainty quantification research of mechatronics system.

1.Introduction

Automatic ammunition loading is one of the key technologies in the development of large caliber artillery to automation, and its main function is to automatically transfer the ammunition from the storage bin to the barrel under the drive of a power device such as a motor[1].Usually,there are strict requirements on the movement of the ammunition delivery mechanism,which needs to complete a wide range of command actions accurately in a very short time(less than 1 s) and with heavy load (about 100 kg load weight).Therefore, it is of great engineering value to comprehensively evaluate the motion accuracy of ammunition delivery mechanism for its practical problems,such as reliability analysis,optimization design,etc.

For an electromechanical systems driven by motors, the movement of the mechanism is planned according to engineering requirements and achieved through controller.In this case, the accuracy of mechanism motion is mainly affected by system parameters, including both mechanical parameters and electrical parameters,and these system parameters are usually random.After the evolution of dynamic system, the uncertainty of system parameters leads to the random distribution of mechanism motion.The uncertainty quantification of dynamic system is an effective way to evaluate the motion accuracy of mechanism [2].About the current research status of the automatic ammunition loading system,researchers mainly from the perspective of multibody system modeling,and robust control algorithm[3,4].On the basis of these works, it is expected to carry out systematic studies of the mechanical and driving devices of ammunition delivery mechanisms,so as to comprehensively evaluate the motion accuracy and provide reference for engineering optimization design.There are two core problems in the accuracy evaluation of ammunition delivery mechanism.The first is to establish the dynamic equation of coupling mechanism and motor operation.The second is to carry out the uncertainty analysis of dynamic system according to stochastic dynamics theory.

Motor as a driver has many advantages,such as high efficiency,portability, etc., is widely recognized in the industry [5].At the same time, the comprehensive study of motor performance to make it widely meet the needs of various engineering,also aroused the great interest of researchers.It is an engineering pursuit to achieve accurate motion and control of low cost and high performance motors.Therefore,scholars have conducted comprehensive research on the motor, including mathematical model, control,position estimation, parameter identification, materials, etc.[5,6]On the one hand, from the perspective of the motor itself, its motion form is a typical rotation around the axis, and the dynamic model can be expressed as Jθ··+ Bfθ·= Te- Tl, in which, J is moment of inertia,Bfis the friction coefficient,Teis electromagnetic torque which is given by the circuit model of the motor, and T is load torque.In carrying load motion, J and T are equivalent quantities on the motor, which are unknown and time varying in most cases.However, in order to improve the performance of position and speed control, it is necessary to accurately identify these parameters.In the study of motor control, Li et al.[7,8] respectively proposed feasible identification methods to obtain the matched and real-time inertia and load parameters,so as to achieve efficient position and speed control.On the other hand, in terms of the dynamics of a multibody system [9], the inertia properties of a mechanism are determined by its material and geometry.Even in the process of motion, its inertia tensor can be obtained by coordinate matrix transformation.When the working condition of the mechanism is determined, its external load source can also be determined, which indicates the generalized load of the dynamic system can also be given accurately.As a result, the physical meaning of the dynamics equation of the multibody system is clear,which is more convenient to study the influence of mechanical parameters on the motion.Li et al.[3,10,11] studied the dynamic modeling of typical mechanisms in automatic ammunition loading systems, including flexible modeling of special structures.This provides an important reference for the dynamic modeling of ammunition delivery mechanism.

The uncertainty analysis of mechanism motion is essentially the uncertainty propagation of dynamic system [12].Uncertainty analysis methods can be divided into two categories: probabilistic method represented by Monte Carlo method [13,14], and nonprobabilistic method represented by interval uncertainty analysis[15,16].The mathematical theory of probabilistic method is more perfect, and the derivation and transmission of uncertainty quantization is more accurate and convenient.A probability density evolution method proposed by Li et al.[17-19] derived the differential governing equation of the joint probability density function through the probability conservation principle in the process of dynamic evolution,and finally solved the probability distribution of the system response by numerical integration, which has the advantages of high precision and small sample size requirement,and can effectively avoid the occurrence of ‘dimensional disaster’.Liu et al.[20,21]conducted modeling research on the core mechanism of automatic ammunition loading system, focusing on the investigation and optimization design of the structural parameters from the perspective of uncertain analysis.Wang et al.[22] applied the probability density evolution method to analyze the uncertainty of ammunition ramming process, obtained the key structural factors affecting the distribution of projectile state, and verified the superiority of this method in the analysis of high dimensional uncertainty problems such as automatic ammunition loading system.

On the basis of these interesting studies, it is expected to carry out more systematic research on the ammunition delivery mechanism, and integrate its driving system and actuating system into the modeling.Then the uncertainty modeling of the whole parameters in the system is carried out in order to quantify the uncertainty of the system response more comprehensively.For this purpose, the electromechanical coupling modeling method and uncertainty quantification of ammunition delivery mechanism are studied in this paper.There are three main achievements of our work.Firstly,a new coupled mechanism-motor dynamic modeling method is proposed.In this method, the relation between mechanism motion and motor rotation is constructed through geometric coordination relation.Therefore,the coupling relationship between the mechanism dynamics and the motor model is more clear.In addition, the physical meaning is more clear to obtain the inertia and load parameters of the model based on the multibody system theory.Secondly,the influence of system parameters on the motion accuracy of the mechanism is discussed comprehensively,including mechanical parameters and electrical parameters.Thirdly,in order to consider the randomness of electric driving load of motor caused by parameter uncertainty, a dynamic simulation framework considering feedback control is constructed,so that the stochastic factors of the system are taken into account more comprehensively in the uncertainty analysis.

The organizational structure of the paper is described below.In Section 2, the basic working principle of ammunition delivery mechanism is introduced, and the geometric relation and load are analyzed comprehensively.On this basis, the mechanism-motor coupling system dynamics model is established, and the strategy of solving the dynamics model including controller is introduced.In Section 3, the uncertainty analysis method of nonlinear system based on generalized probability density evolution equation is discussed and the uncertainty parameters of ammunition delivery system are analyzed in detail.Next,we discuss the results in Section 4, including the experimental verification of the proposed model and the results of motion uncertainty under various working conditions.Based on the above work, Section 5 gives the summary of the full paper.

2.Coupled mechanism-motor model of ammunition delivery system

2.1.Basic principles of attitude adjustment motion

Fig.1 shows the system composition of an ammunition automatic loading system, which is mainly composed of ammunition swing manipulator, ammunition delivery mechanism and related drive system.It is a typical mechatronics system.In the actual work project,the manipulator motor drives the ammunition manipulator to rotate around the axis, and drives the ammunition delivery mechanism to complete the space conversion from the ammunition storage bin to the breech.At the same time, the attitude adjustment motor drives the expansion of the lead screw,drives the ammunition delivery mechanism to rotate around the rotating axis,and realizes the attitude adjustment from the position of receiving ammunition(coaxial with the outlet of ammunition storage bin)to the position of conveying ammunition (coaxial with the gun barrel).

Fig.1.Ammunition automatic loading system.

In the whole working process, compared with the ammunition manipulator, the attitude adjustment motion of the ammunition conveying mechanism includes two working conditions: a) The ammunition delivery mechanism transfers from the conveying ammunition position to the receiving ammunition position;b)The ammunition delivery mechanism transfers from the receiving ammunition position to the conveying ammunition position.

2.2.Geometric coordination relations of attitude adjustment motion

Fig.2 shows the schematic diagram of the attitude adjustment motion of the ammunition delivery mechanism.The motor support and the rotating shaft are respectively fixed on the ammunition manipulator.During attitude adjustment, the motor and ammunition delivery mechanism rotate around the rotation center A and O respectively.The lead screw is connected to the ammunition delivery mechanism through a rotating pair,and it rotates relative to center B.Driven by the motor, the lead screw stretches drives the ammunition delivery mechanism to rotate.Wherein, under the working condition a), the lead screw shrinks and the motor turns positive; Under working condition b), the lead screw is extended and the motor is reversed.

In the actual working process,the angle of motor rotation Δθmis proportional to the lead screw expansion length ΔlAB.The angle of ammunition delivery mechanism and the length of lead screw should meet the geometric coordination relationship.Therefore,the following coordination relationship is satisfied between the attitude adjustment motion of ammunition delivery mechanism and the rotation of motor:

in which, kris the proportional coefficient, and θOis the angle of∠AOB.

The angle of ∠AOB at the initial time is denoted as φ0, and the angular displacement of the ammunition delivery mechanism is θz.There is a relationship between them, and that is, θO= φ0- θz.Take the derivative of Eq.(1) with respect to time,

Fig.2.Schematic diagram of attitude adjustment motion of ammunition delivery mechanism.

2.3.Load analysis of ammunition delivery mechanism

The main considerations of external load in the system are gravity FG,the driving load FItransmitted by the lead screw and the contact load Fcgenerated by the clearance at the rotating joint.

The lead screw driving load is given by model (3).

in which,Τerepresents the electromagnetic torque of the motor,k1is the transmission coefficient between the motor and the lead screw, and η indicates the efficiency of the system.

There are many classic contact models, such as Hertz model,Hunt-Crossley model, Flores model, Lankarani-Nikravesh model,etc.[23].The Lankarani-Nikravesh model considering hysteretic damping factor, which separates the normal contact force into elastic and dissipative components, and was widely applied to dynamics analysis of mechanical systems with revolute clearance joints and it shows good precision [24].For the contact collision between shaft and hole with clearance as shown in Fig.3,Lankarani-Nikravesh normal contact model Fnand improved Coulomb tangential friction model Ftare used for contact loads Fcrespectively[25].

in which, Kcis the contact stiffness coefficient, n is a nonlinear exponential, cerepresents the restitution coefficient, cfand cdrespectively refer to friction coefficient and friction correction coefficient,vtis the tangential velocity vector.are contact penetration,penetration velocity and initial velocity before contact respectively.

2.4.Coupled mechanism-motor dynamic model

Considering that a mechanism satisfies kinematic constraint C(q,t)=0,the dynamic equation of the mechanism can be expressed as Eq.(5) [9]:realized by motor control,using PI control algorithm.In this paper,the actual control strategy of ammunition delivery mechanism is introduced into the solution of attitude adjustment dynamic model, as shown in Fig.4.Different from using sensor monitoring as feedback in engineering,this paper is based on model simulation results as feedback.The control strategy of attitude adjustment motion includes position loop, speed loop and current loop.The id= 0 strategy is used in the actual motor control of attitude adjustment motion.Therefore,only iqis considered in this analysis.Algorithm 1.introduces the process of solving the dynamic response of the coupled motor control strategy.In addition,considering the motor limiting, the motor speed is set between-1500 rpm and 2500 rpm,where the minus sign indicates reversal.

Fig.3.Diagram of contact between shaft and hole with clearance.

Algorithm 1 Solution of Mechanism-motor coupling dynamic model for attitude adjustment motion 1： Input：θn,θn·,In, ^θn+1 m 2： Output：θn+1,θn+·1, In+1 3: Calculate the motor position θnm and speed θ·m n: Eqs.(1) and (2)//Position error at step n 4： enr ←^θn+1 m -θn m//Position loop PI to calculate the instruction speed 5： θ·m n+1←fr（enr）//Speed error at step n 6： env ←■θn+1m - θ·m n//Speed loop PI to calculate the instruction current 7: enI ←^In+1- In//Current error at step n 8： enI -In+1 - In//Current loop PI to calculate the instruction voltage 9： ^un+1←fI（enI）10： Calculate the response at step n+1： Runge-Kutta method to solve differential equation Eq.(7)

Remark: For a particular mechanism, its inertia parameters is determined by its material and geometric distribution.The inertia tensor during the motion of the mechanism can also be determined by coordinate transformation.This means that the mass matrix in Eq.(7),although time varying,is solvable.Besides,the generalized load vector under specific working conditions is also clear.As a consequence,the physical meaning of parameters based on Eq.(7)is more clear, and the expression can be conveniently given from the theory of multibody system[9].

2.5.Introduction to attitude adjustment motion control strategy

In engineering practice, attitude adjustment movement is

3.Uncertainty quantification theory for nonlinear dynamical systems

3.1.Random parameter analysis of ammunition delivery system

For ammunition delivery system, there are many parameters that cause its motion uncertainty.In addition to the mechanical parameters related to the mechanism, the electrical parameters inside the motor will also affect the motion to a certain extent.In view of the coupled mechanism-motor dynamics model established in Section 2 of this paper,we can consider the uncertainty of mechanical and motor parameters synthetically.

For these uncertain parameters in the ammunition delivery system,this paper focuses on random quantities with clear physical meaning in engineering, significant influence on mechanism motion and convenient access to statistical information.These random parameters are denoted as ξ and they include:

(1) Mechanical parameters

· The mass of the mechanism, M

· The moment of inertia,Jz

· The eccentricity of the mass center in the x directions, Dx

· The eccentricity of the mass center in the y directions, Dy

· The eccentricity of the mass center in the y directions, Dy

(2) Electrical parameters

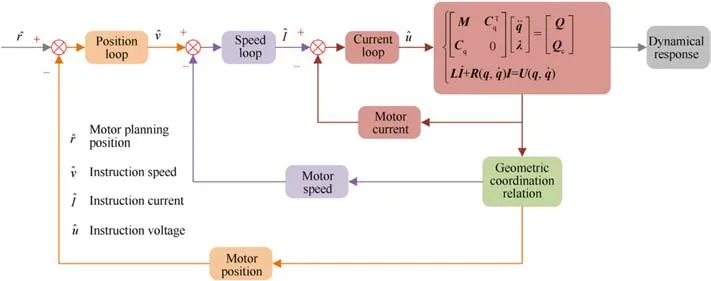
Fig.4.Control strategy of motor.

· The inductance, Lq

· The resistance, Rs

· The flux linkage,ψf.

3.2.Generalized probability density evolution equation

There are many methods of uncertainty analysis,among which generalized probability density evolution method has the advantages of high precision and small sample size requirement,and can effectively avoid the occurrence of 'dimensional disaster'[17-19,22], and is suitable for high dimensional uncertainty problems of ammunition delivery system.

The mechanical-motor coupling model of ammunition delivery system is essentially a second order dynamical system governing equation, and is characterized by random parameters ξ Without loss of generality, we reconsider model (7) as a parameterized dynamic system:

in which, Ω?Rnis the n-dimensional space domain, τ= [0,T]represents the time domain, and Γ?Rmindicates the m-dimensional random variable space.ξ=[ξ1...ξm] is a m-dimensional random variable, and they have a prescribed joint probability density distribution ρξ.N (·) is a nonlinear differential operator.u=u（x,t,ξ）represents the state response of the dynamical system.

The discrete solutions of response variable u controlled by Eq.(8)are denoted as X（ξ,t）∈RNuand X·（ξ,t）∈RNurespectively,where Nuis the degrees of freedom.The joint probability density function ρξ（X,ξ,t）of the system random response X and random variable ξ satisfies the generalized probability density evolution equation[2,27,28]:

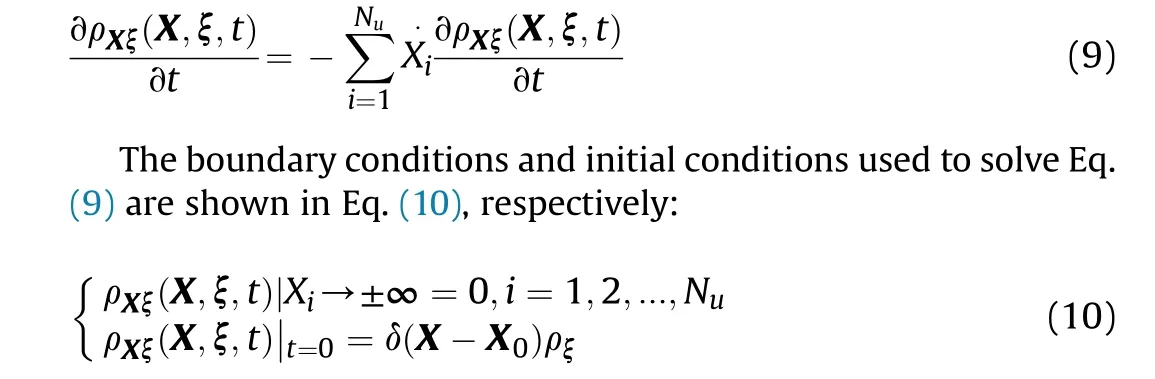
Integrate the joint probability density function ρXξ（X,ξ,t）in the random variable space Γ to obtain the joint probability density function ρX（X,t） of the random response of the system.

By solving Eq.(12) and integrating according to Eq.(11), the probability density distribution function ρXiξ（Xi,ξ,t） of the interesting response variable Xican be obtained.

3.3.Introduction to numerical computation scheme

The generalized probability density evolution equation expressed in Eq.(12) belongs to hyperbolic partial differential equation.In this paper, the Lax-Wendroff scheme is adopted to solve it numerically[29].Consider the general form of the equation without loss of generality:

p（x,t） is discretized in spatial domain and time domain respectively, yields pkj.The subscript j represents a mesh point on the spatial domain with dimension Δx.The superscript k represents a discrete point in the time domain with step size Δt.Taylor expansion of p on the interval [kΔt,（k + 1）Δt].

Consequently, the update scheme is shown as

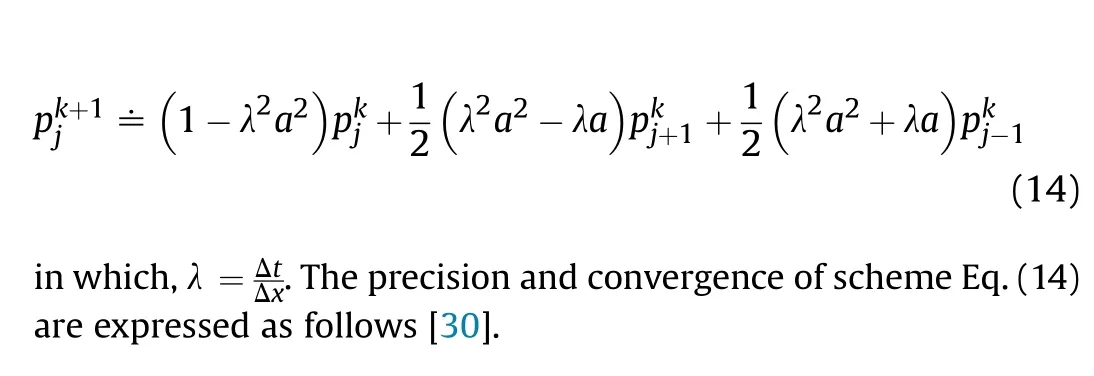
Theorem.1.The Lax-Wendroff discrete scheme has second-order precision in both time and spatial domain.

Fig.5.Automatic ammunition loading experiment test system.

Theorem.2.The convergence condition of Lax-Wendroff scheme is: |a|λ ≤1.

4.Results and discussion

4.1.Model verification

In this section, combined with the automatic ammunition loading test system shown in Fig.5,the mechanism-motor coupling dynamic model of the attitude adjustment motion proposed in this paper is verified.In addition,the nonlinear exponential n=1.5,the restitution coefficient ce=0.46,and the material of the mechanism is steel.

Fig.6 shows the response curves of angular displacement and angular velocity of the ammunition delivery mechanism obtained by testing and numerical simulation under two working conditions.The results in the figure show that the proposed model can get highly consistent response results with the experiment.Furthermore,based on the model,we discuss the influence of the clearance of the rotating pair on the dynamic response of attitude adjustment motion.Fig.7 shows the response curve of angular velocity of the mechanism under different clearances.The results in the figure indicate that the existence of clearance will cause obvious oscillation of the mechanism velocity, which will affect the motion accuracy.

4.2.Influence of mechanical parameters on motion accuracy

Fig.6.Dynamic response curve of ammunition delivery mechanism under two different working conditions: pair: (a) Working condition a; (b) Working condition b.

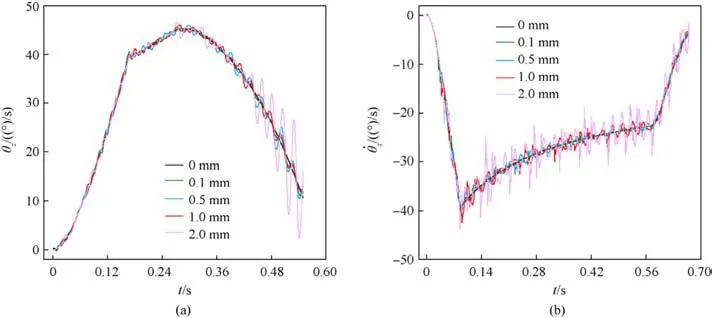
Fig.7.Dynamic response curve of mechanism with different clearance sizes of rotating pair: (a) Working condition a; (b) Working condition b.

The influence of mechanical random parameters, such as mass and inertia, is usually emphasized in the study of kinematic uncertainty of mechanism.This paper firstly studies the influence of two kinds of parameter uncertainties on the kinematic accuracy of mechanism separately, to verify the effect of electrical parameters on the mechanism motion accuracy.

In this section, we independently investigate the influence of the uncertainty mechanical parameters on the motion accuracy of the mechanism.The distribution of these parameters is detailed in Table 1.In the table, the random distribution of mechanical parameters is mainly obtained according to Refs.[31,32] and engineering experience.

In this study,500 groups of data are sampled in the probability space of the input parameters employing a point selection technique based on the generalized F-deviation [33].Fig.8 shows the random distribution curve of rotation angle of ammunition delivery mechanism caused by uncertainty of structural parameters under different rotation pair clearance.According to our statistics, the mean μ and variance σ are shown in Table 2.It can be concluded that due to the uncertainty of mechanical parameters,the response of the dynamic system will have a random evolution,resulting in a random distribution of the rotation angle of the mechanism at the end, that is, the motion accuracy will be affected.The statistical results show that the clearance affects both the mean and variance of the distribution at the end of rotation.In particular,the larger the clearance, the larger the variance, indicating the larger the distribution of motion, which implies that the motion accuracy is poor.

It is well known that electromechanical systems can achievehigh efficiency and high precision motion under feedback control.As a results, we conducted a comparative study on the motion accuracy of the mechanism without feedback control,and the results are shown in Fig.9.It should be noted that,without considering the motor control, we take the current obtained from the test as the driving load that does not change with the working condition,so as to study the angle distribution of the mechanism under the random distribution of structural parameters.The statistical results are μ = 16.5002°and σ = 17.3042°.We can clearly find that without feedback control, the motion accuracy of the mechanism is poor,which is undoubtedly difficult to meet the engineering requirements.

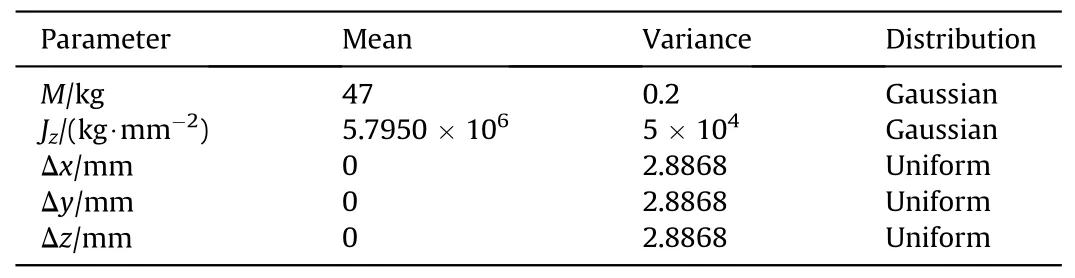
Table 1 Random distribution of mechanical parameters.

Fig.8.The probability density distribution function of rotation angle θz at the final moment of motion under different clearance.

Table 2 Statistical results of rotation distribution under different clearance.

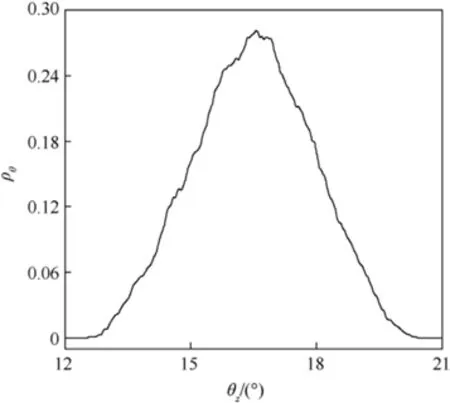
Fig.9.The probability density distribution function of rotation angle θz without feedback control.

4.3.Influence of electrical parameters on motion accuracy

In order to investigate the influence of electrical parameters on the motion accuracy of the mechanism,the uncertainty of electrical parameters is further analyzed separately in this section.The distribution of these parameters is detailed in Table 3.In the table,the random distribution of electrical parameters is mainly obtained by consulting manufacturers.

Fig.10 shows the random distribution curve of rotation angle of ammunition delivery mechanism caused by uncertainty of structural parameters under different rotation pair clearance.

Statistical results show that the mean μ and variance σ are as shown in Table 4.It is not difficult to find that the electrical parameters also have an obvious influence on the motion accuracy of the mechanism, which is even greater than the mechanical parameters.This conclusion also highlights the superiority of the mechanism-motor coupling model established in this paper,that is,various system parameters can be considered more comprehensively in the mechanism dynamics analysis.

4.4.Comprehensive analysis of mechanism motion accuracy

Finally, we discuss the stochastic distribution and evolution of mechanism motion under the combined influence of structural andelectrical parameters.Fig.11 shows the probability distribution curve of mechanism rotation in a period of 0.52-0.55 s without considering the clearance of rotating pairs.As can be seen from the figure,the uncertainty of system parameters leads to the evolution of its response probability distribution with time.

Table 3 Random distribution of electrical parameters.

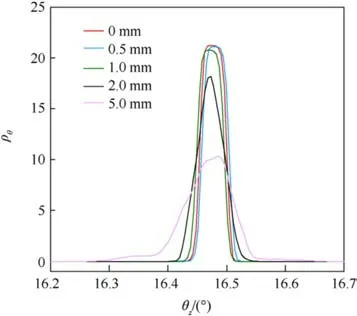
Fig.10.The probability density distribution function of rotation angle θz without feedback control.

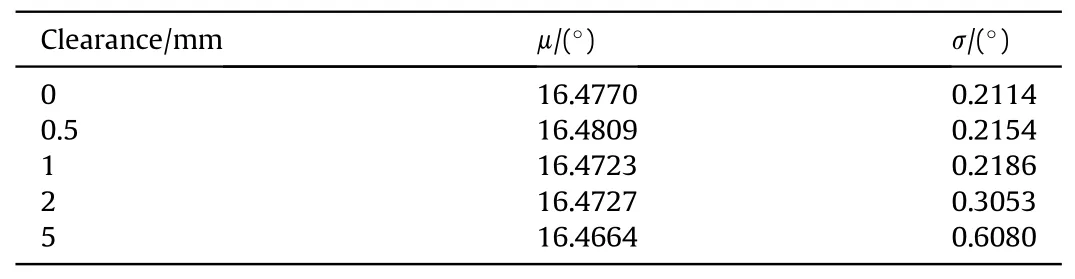
Table 4 Statistical results of rotation distribution under different clearance.

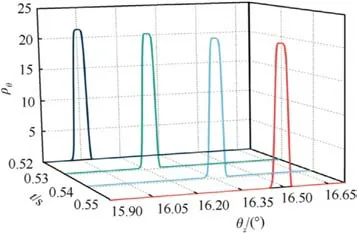
Fig.11.Probability density evolution of mechanism angle θz.

The random evolution process of ammunition delivery mechanism rotation is statistically analyzed,and the results are shown in Fig.12.It is not difficult to draw two important conclusions from the results in the figure.Firstly, the evolution of the mean value matches the dynamic process.Secondly,with the evolution of time,the variance increases,which implies that the distribution interval of motion increases, that is, the accuracy decreases.

5.Conclusions

In this paper, a coupled mechanics-motor dynamics model is proposed, which the coupling between mechanism dynamics and motor model is described more intuitively, and can conveniently study the effects of system mechanical parameters and electrical parameters on the mechanism motion.Taking ammunition conveying mechanism as an example, the feasibility of the modeling method proposed in this paper is verified by experiments, and the influence of the clearance of rotating pair on the kinematic response of the mechanism is studied.Then, the influence of system parameter randomness on kinematic accuracy of mechanism is investigated from the perspective of uncertainty quantification.

The results show that the randomness of mechanical parameters and electrical parameters will both lead to the uncertain distribution of dynamic response.The introduction of controller is very beneficial to the improvement of motion accuracy.The clearance of rotating pair is unfavorable to the motion accuracy of mechanism.When there is no gap between the rotating pairs of the mechanism, the variance of the angular distribution is about 0.21.However, when the clearance increases to 5 mm, the variance increases to about 0.6.In addition, With the evolution of time, the statistical mean of mechanism motion is matched with the dynamic process,but the interval distribution of motion will increase.

In conclusion,the work of this paper can not only provide help for the further study of the dynamics,reliability,control and other engineering problems of ammunition delivery system, but also guide the modeling and uncertainty quantitative research of electromechanical system systematically.

Fig.12.Statistical results of uncertainty evolution for ammunition delivery mechanism:(a)Mean value evolution and dynamic simulation;(b)The evolution curve of the variance curve.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos.11472137 and U2141246).