盧定波

菱形是特殊的平行四邊形,具有平行四邊形的所有性質(zhì).另外,菱形還具有特別的性質(zhì):菱形的四條邊都相等,對角線互相垂直,并且每條對角線平分一組對角.

例1 (2008年·宜賓)如圖1,菱形ABCD中,E?F分別是BC?CD上的點,且BE=DF.求證:AE=AF.

解析:由“菱形的四條邊都相等”可知AB=AD.由“菱形對角相等”可得∠B=∠D.再由已知BE=DF,運用SAS可判定△ABE≌△ADF.從而可證明AE=AF.

點評:解本題主要運用了菱形的四條邊都相等和對角相等的性質(zhì),并結(jié)合全等三角形來證明線段相等.也可連接AC,由SAS證△AEC≌△AFC.

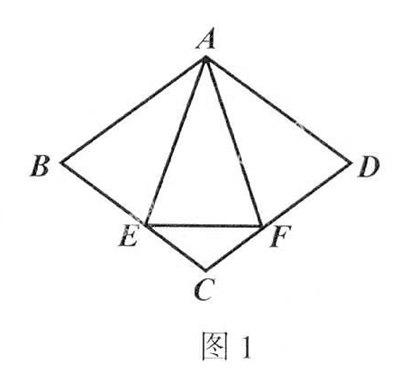
例2 (2008年·廣州)如圖2,在菱形ABCD中,∠DAB=60°.過點C作CE⊥AC,且與AB的延長線交于點E.求證:AD=CE.

解析:由于AC為菱形的對角線,可知∠CAB=∠DAC=30°.因為CE⊥AC,所以∠E=60°.由AD∥BC,可知∠CBE=∠DAB=60°=∠E,所以BC=CE.再由AD=BC,從而可得AD=CE.

點評:本題還可連接BD,由BD⊥AC知BD∥CE.易知四邊形BDCE為平行四邊形.AD=BD=CE.

例3 (2007年·嘉興)如圖3所示,在菱形ABCD中,不一定成立的是( ).

A. 四邊形ABCD是平行四邊形

B. AC⊥BD

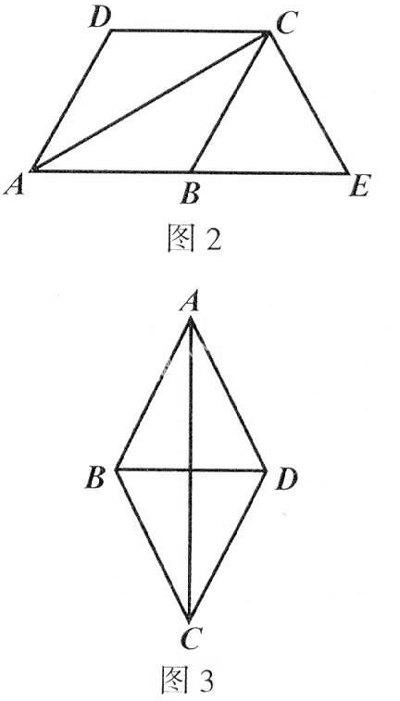
C. △ABD是等邊三角形

D. ∠CAB=∠CAD

解析:由菱形的定義,可知菱形也是平行四邊形,故選項A是對的.由“菱形的對角線互相垂直”,可知選項B是正確的.由“菱形的對角線平分一組對角”,可知選項D也是正確的.由“菱形的四條邊都相等”可知, △ABD是等腰三角形,但對角線BD與菱形的四條邊不一定相等,因此△ABD不一定是等邊三角形.只有當(dāng)BD與菱形的邊相等時, △ABD才是等邊三角形.因此,選項C不一定成立.

點評:本題要求學(xué)生能夠熟練地將“文字語言”(定義?性質(zhì)等)結(jié)合具體的圖形轉(zhuǎn)化為“幾何語言”.

例4 如圖4,菱形ABCD的周長為40,點 O是兩條對角線AC?BD的交點,且AC∶BD=3∶4.求AC和BD的長.

解析:由“菱形的四條邊都相等”,可知AB=1/4×40=10.根據(jù)“菱形的對角線互相垂直平分”,可得∠AOB=90°,OA=1/2AC, OB=1/2BD.因AC∶BD=3∶4,所以有OA∶OB=3∶4.不妨設(shè)OA=3x,則OB=4x.在

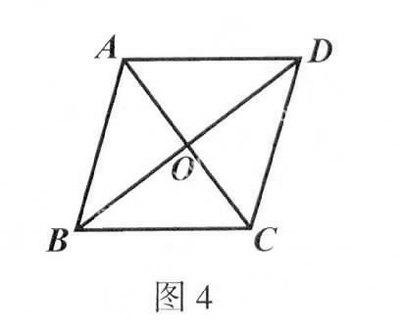
Rt△OAB中,由勾股定理,可知OA2+OB2=AB2,即(3x)2+(4x)2=102,解得x=2.因此OA=3x=6, OB=4x=8,所以AC=2OA=12,BD=2OB=16.

點評:求菱形的邊長或?qū)蔷€長的問題,都是利用菱形的性質(zhì),在由邊長和兩條對角線的一半組成的直角三角形中,運用直角三角形的性質(zhì)(如30°角所對的邊長是斜邊長的一半)或勾股定理求解的.

例5 (2008年·大連)如圖5,菱形ABCD和菱形QMNP中,∠NMQ =∠ABC,點M是菱形ABCD的對角線AC?BD的交點, MN交AD于點F,MQ交AB于點E.試探究ME與 MF有何關(guān)系.請說明你的理由.

解析: ME= MF.理由如下.

過點M分別作MH⊥AB于點H,MR⊥AD于點R.如圖6.

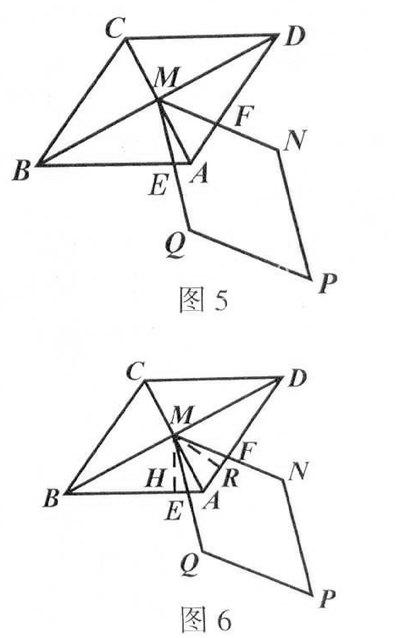
由“菱形的對角線平分一組對角”,可知點M在∠BAD的平分線上.又因為MH⊥AB, MR⊥AD,可得MH=MR.又∠HME+∠EMR=∠HMR=∠ABC(想想為什么),∠RMF+∠EMR=∠NMQ=∠ABC,所以∠HME=∠RMF.根據(jù)ASA可判定△HME≌△RMF,所以ME=MF.

點評:本題是一道結(jié)論探究題,運用了“角平分線上的點到這個角兩邊的距離相等”等相關(guān)知識,是一道綜合性較強的好題.

菱形的性質(zhì)較多.在解題中,要根據(jù)解題的需要, 選用菱形的相關(guān)性質(zhì).另外,要注意菱形對角線與等腰三角形?直角三角形的緊密聯(lián)系.