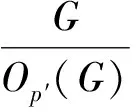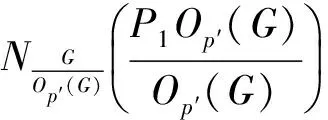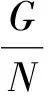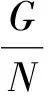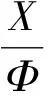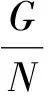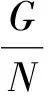張新建

(淮陰師范學(xué)院 數(shù)學(xué)科學(xué)學(xué)院,江蘇 淮安　223300)

0　引言

本文考慮的是有限群,G總是表示群,H?G表示H是G的正規(guī)子群,其他符號(hào)和概念是標(biāo)準(zhǔn)的,可參見(jiàn)文獻(xiàn)[1].

群G的子群H和T稱為是可置換的,如果HT=TH.群G的子群H稱為G的S-擬正規(guī)(或π-擬正規(guī))子群[2],如果H與G的每個(gè)Sylow子群可置換;H稱為G的S-擬正規(guī)嵌入子群[3],如果對(duì)每個(gè)整除H的素因子p,H的一個(gè)Sylowp-子群也是G的某個(gè)S-擬正規(guī)子群的Sylow p-子群.

一方面,在文獻(xiàn)[4]中,作者利用群G的所有pm階子群的S-擬正規(guī)嵌入性質(zhì)研究群G的結(jié)構(gòu),得到了主要的定理:

定理A設(shè)p是G的階的最小素因子,P是G的一個(gè)Sylowp-子群,則G是p-冪零群當(dāng)且僅當(dāng)存在P的子群D滿足1<|D|<|P|使得P的所有階為|D|或4(當(dāng)|D|=2時(shí))的子群在G中S-擬正規(guī)嵌入.

定理B設(shè)p為G的階的奇素因子,P是G的一個(gè)Sylow p-子群,則G是p-冪零群當(dāng)且僅當(dāng)NG(P)是p-冪零群且存在P的子群D滿足1<|D|<|P|使得P的所有階為|D|的子群在G中S-擬正規(guī)嵌入.

另一方面,著名的Frobenius定理[1]斷言:如果群G的所有的p-子群H的正規(guī)化子NG(H)是p-冪零群,那么G是p-冪零群.

在本文中,我們利用群G的所有pm階子群H的正規(guī)化子的p-冪零性及H的S-擬正規(guī)嵌入性得到了群G的p-冪零性的一個(gè)判定定理:

定理2設(shè)p為G的階的奇素因子,P是G的一個(gè)Sylow p-子群,則G是p-冪零群當(dāng)且僅當(dāng)且存在P的子群D滿足1<|D|<|P|使得P的所有階為|D|的子群H在G中S-擬正規(guī)嵌入且NG(H)是p-冪零群.

1　主要引理

引理1[2]假設(shè)U是G的S-擬正規(guī)嵌入子群,H是G的子群,N是G的正規(guī)子群.

(a) 如果U≤H,則U是H的S-擬正規(guī)嵌入子群.

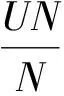
引理2[1]G的S-擬正規(guī)子群在G中次正規(guī).

引理3[5]設(shè)H是G的S-擬正規(guī)子群,P是H的Sylow p-子群,其中p是素?cái)?shù).如果HG=1,那么P是G的S-擬正規(guī)子群.

引理4[4]設(shè)N是G的初等交換正規(guī)子群.如果N有子群D滿足1

引理5[6]假設(shè)p是素?cái)?shù),G是非p-冪零群但G的每個(gè)真子群是p-冪零群.則

(a)G有正規(guī)的Sylowp-子群P且G=PQ,其中Q是非正規(guī)的Sylowq-子群,q≠p.

(c)P的冪指數(shù)為p或4.

2　主要結(jié)論

定理1設(shè)P為群G的一個(gè)Sylowp-子群,其中p∈π(G).則G是p-冪零群當(dāng)且僅當(dāng)P的每個(gè)極大子群P1在G中S-擬正規(guī)嵌入且NG(P1)是p-冪零群.

證明如果G是p-冪零群,那么G=[Op′(G)]P.設(shè)H是P的任一極大子群.NG(H)的p-冪零性是顯然的.由HOp′(G)?POp′(G)=G可知H在G中S-擬正規(guī)嵌入.

反之,假設(shè)結(jié)論不正確,G為滿足條件的極小階反例,則有

1)p為奇素?cái)?shù).如果p=2,那么由文獻(xiàn)[7]中定理3.1可得G是p-冪零群,矛盾.

則P1Op′(G)?K,因此K=NK(P1)P1Op′(G)=NG(P1)Op′(G)≤K,這意味著

3) 設(shè)T是G的包含P的真子群,則T是p-冪零群.

設(shè)P1是P的任一極大子群.顯然NT(P1)≤NG(P1).由假設(shè),我們有NT(P1)是p-冪零群.又由引理1,P1在T中S-擬正規(guī)嵌入.因此T滿足定理的假設(shè),由G的極小性選擇可得T是p-冪零群.

5) |P|=|N|=p,最后的矛盾.

由4),Φ(G)=1,于是G有極大子群M使得G=MN且M∩N=1.顯然,P=N(P∩M).因?yàn)镻∩M

因此反例不存在,結(jié)論得證.

定理2設(shè)p為群G的階的奇素因子,P是G的一個(gè)Sylow p-子群,則G是p-冪零群當(dāng)且僅當(dāng)且存在P的子群D滿足1<|D|<|P|使得P的所有階為|D|的子群H在G中S-擬正規(guī)嵌入且NG(H)是p-冪零群.

證明若G是p-冪零群,則由定理1可知結(jié)論是成立的.反之,假設(shè)結(jié)論不正確,G為滿足條件的極小階反例.

1) 設(shè)T是包含P的G的真子群,則T是p-冪零群.

證明類似于定理1的證明中的3).

2) |P:D|>p且|D|>p.

3)Op(G)≠1.令N是包含在Op(G)中的G的極小正規(guī)子群,則|N|<|D|.

因?yàn)镚是非p-冪零群,由(1)和Glauberman-Thompson定理,NG(Z(J(P)))是非p-冪零群,其中J(P)是P的Thompson子群.注意到Z(J(P))是P的特征子群,NG(P)≤NG(Z(J(P))).由3),我們有NG(Z(J(P)))=G,這意味著Op(G)≠1.如果|N|=|D|,那么由假設(shè),G=NG(N)是p-冪零群,矛盾.假設(shè)|N|>|D|,因?yàn)镹≤Op(G),N是初等交換群.由引理4,N有極大子群在G中正規(guī),則由N的極小正規(guī)性可得|N|=p,從而|D|=1,矛盾于假設(shè).因此|N|<|D|.

5) 得到結(jié)論.

參考文獻(xiàn)：

[1]Hupper B T. Endliche Gruppen I[M]. New York: Springer-Berlin,1967.

[2]Kegel O H. Sylow-Gruppen and Subnoramlteiler endlicher Gruppen[J]. Math Z,1962,78: 205-221.

[3]Ballester-Bolinches A,Pedraza-Aguilera M C. Sufficient conditions for supersolubility of finite groups[J]. Journal of Pure and Applied Algebra,1998,127: 113-118.

[4]Wei X B ,Guo X Y. On finite groups with prime-power order S-quasinormally embedded subgroups[J]. Monatsh Math,2011,162(3): 329-339.

[5]Wei H Q,Wang Y M. On c*-normality and its properties[J]. Journal of Group Theory,2007,10: 211-223.

[6]Guo W B. The Theory of Classes of Groups[M]. Beijing: Science Press,2000.

[7]Asaad,M,Heliel A A. On S-quasinormally embedded subgroups of finite groups[J]. Journal of Pure and Applied Algebra,2001,165:129-135.

[8]Li Y M,Wang Y M,Wei H Q. The influence ofπ-quasinormal of some subgroups of a finite group[J]. Arch Math,2003,81: 245-252.

[9]Robinson D J S. A course in the Theory of Groups[M]. New York: Springer-Berlin,1993.

[10]Gorenstein D. Finite Groups[M],New York: Harper and Row,1968.