負(fù)二項(xiàng)分布的廣義線性模型及其應(yīng)用
陳卓恒
(華僑大學(xué)數(shù)學(xué)科學(xué)學(xué)院,福建泉州 362021)
負(fù)二項(xiàng)分布的廣義線性模型及其應(yīng)用
陳卓恒
(華僑大學(xué)數(shù)學(xué)科學(xué)學(xué)院,福建泉州 362021)
討論一類散度偏大的分布負(fù)二項(xiàng)分布的相關(guān)性質(zhì),以服從負(fù)二項(xiàng)分布的索賠次數(shù)為響應(yīng)變量,引入風(fēng)險(xiǎn)分級變量和對數(shù)聯(lián)結(jié)函數(shù),建立廣義線性模型.采用極大似然估計(jì)法進(jìn)行參數(shù)估計(jì),并用Wald檢驗(yàn)法進(jìn)行檢驗(yàn).最后,利用SAS軟件包對一組保險(xiǎn)索賠數(shù)據(jù)進(jìn)行實(shí)證分析.
負(fù)二項(xiàng)分布;廣義線性模型;Wald檢驗(yàn);風(fēng)險(xiǎn)分級
在風(fēng)險(xiǎn)理論中,總索賠次數(shù)的分布的研究一直是個(gè)中心論題.一般情況下,常采用均值等于方差的Poisson分布來描述索賠次數(shù)分布,但這與實(shí)際情況是不符的.事實(shí)上,索賠次數(shù)的分布規(guī)律往往偏離實(shí)際出事故次數(shù)的分布規(guī)律.鑒于此,本文引入方差大于均值的分布負(fù)二項(xiàng)(NB)分布,并在此基礎(chǔ)上建立相應(yīng)的廣義線性模型.
1 負(fù)二項(xiàng)分布的性質(zhì)
對于風(fēng)險(xiǎn)非同質(zhì)性保單組合而言,索賠次數(shù)往往可用混合Poisson分布來擬合.即索賠次數(shù)滿足
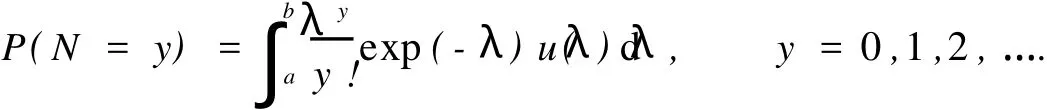
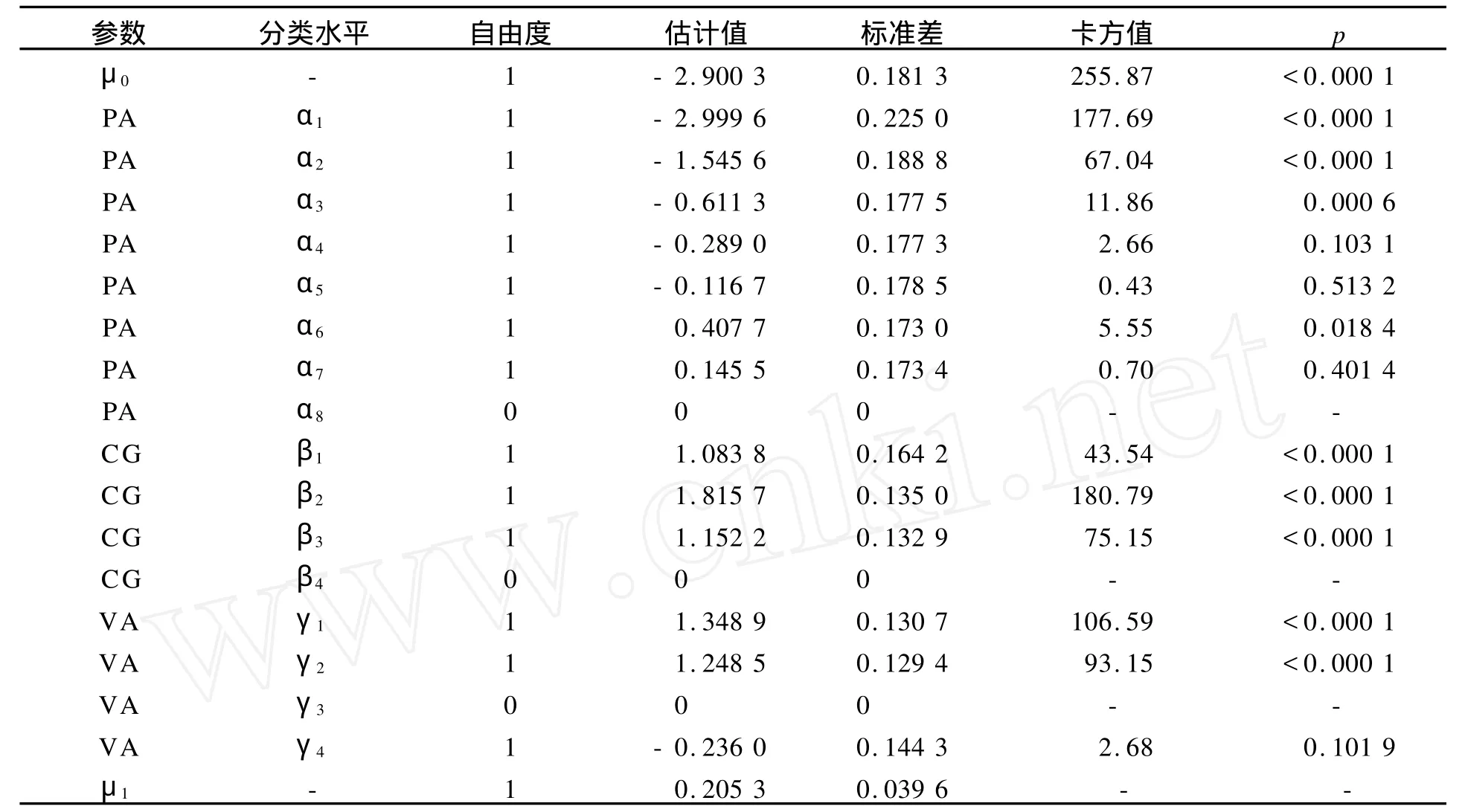
其中:u(λ)是某個(gè)區(qū)間[a,b]上某連續(xù)分布的密度函數(shù),0≤a 此時(shí)的索賠次數(shù)N服從負(fù)二項(xiàng)分布.若記α=r,β=r/μ,則帶參數(shù)r和μ(r>0)的負(fù)二項(xiàng)分布的概率函數(shù)又可表示為 由負(fù)二項(xiàng)分布的性質(zhì),易得 2.1 模型的建立 廣義線性模型是由Nelder提出的,十分適合離散的,厚尾的保險(xiǎn)數(shù)據(jù).它對于傳統(tǒng)線性模型有以下3個(gè)方面的推廣. (1)響應(yīng)變量Y的分布,可以取自于指數(shù)型分布族中的任一種分布. (2)自變量的線性組合為η=β1x1+…+βk xk=X′β.這與多元線性回歸模型沒有什么區(qū)別,Y,X可取連續(xù)或離散值,但在應(yīng)用上更多的是取離散值. (3)響應(yīng)變量的均值E(Y)=μ=h(X′β),h單調(diào)且可導(dǎo),其反函數(shù)g=h-1稱為聯(lián)結(jié)函數(shù). 設(shè)某險(xiǎn)種的保單按其屬性分為n類風(fēng)險(xiǎn)組,Yi表示第i類保單的索賠次數(shù),且Yi服從于NB(μi, r),i=1,2,…,n,Yi之間相互獨(dú)立.這里的r可看成冗余參數(shù),在各次觀察中不變.X為風(fēng)險(xiǎn)分級變量,采用對數(shù)聯(lián)結(jié)函數(shù)g(x)=log(x)建立廣義線性模型,有 式中:Xi=(xi,1,xi,2,…,xi,k)′,β為k維待估參數(shù). 2.2 極大似然估計(jì) 考慮用極大似然估計(jì)法進(jìn)行參數(shù)估計(jì).對于獨(dú)立樣本(Xi,Yi′),i=1,2,…,n,把Y的分布寫成指數(shù)標(biāo)準(zhǔn)型,有 由于一維指數(shù)型分布的分布密度(概率函數(shù))的標(biāo)準(zhǔn)形式為 將式(5)對應(yīng)于式(6),即有 由于μi=exp(Xi′β),因此式(5)中的θi與Xi有關(guān),與參數(shù)β也有關(guān).似然函數(shù)為 而對數(shù)似然為 由式(3)可得 由指數(shù)標(biāo)準(zhǔn)型分布的常用結(jié)論,易知 于是,由式(11),(12),(13)可得 因此,似然方程(10)又可寫成 一般來說,在一定條件下,滿足似然方程=0的極大似然解(MLE)β是存在且唯一的[3]. 2.3 MLE的迭代計(jì)算 則從初始值β(0)開始,第k步算到β(k),并采用迭代式 式中:H-1(β)表示式(18)的H(β)逆矩陣.對于設(shè)定的ε,當(dāng)進(jìn)行到‖β(k+1)-β(k)‖/‖β(k)‖<ε時(shí),即停止迭代.初始條件β(0)可取為{(g(yi),Xi),1≤i≤n}下線性回歸系數(shù)的LS估計(jì),即 式(19)最終可化為一個(gè)加權(quán)最小二乘估計(jì)的形式,并通過采用SAS軟件包中線性回歸的程序?qū)崿F(xiàn). 2.4 假設(shè)檢驗(yàn) 檢驗(yàn)部分采用Wald檢驗(yàn).由于模型的選擇和解釋變量的顯著性檢驗(yàn)問題可化為線性假設(shè)檢驗(yàn),原假設(shè)H0∶Cβ=ξ,備則假設(shè)H1∶Cβ≠ξ.其中,C為s×k的行滿秩矩陣,β為k維向量. 引入Wald統(tǒng)計(jì)量,即W=(Cβ-ξ)′[CH-1(β)C′]-1(Cβ-ξ).這里的β表示β的MLE,當(dāng)原假設(shè)成立時(shí),W d服從于χ2(s),即統(tǒng)計(jì)量W漸進(jìn)服從自由度為s的χ2分布.所以,對于給定檢驗(yàn)水平α(0<α<1),若W>χ2α(s),則拒絕原假設(shè)H0;否則,接受H0. 數(shù)據(jù)來源于某保險(xiǎn)公司關(guān)于機(jī)動車輛的保險(xiǎn)索賠資料[4-5],如表1所示.考慮有如下3種風(fēng)險(xiǎn)因素影響著索賠額(N)和索賠次數(shù)(Y):(1)保單持有者的年齡(PA).有17~20歲,21~24歲,25~29歲, 30~34歲,35~39歲,40~49歲,50~59歲,60歲以上8個(gè)水平,分別用α1~α8表示;(2)車型(CG).有A,B,C,D共4個(gè)水平,分別用β1~β4表示;(3)車齡(VA).有0~3 a,4~7 a,8~9 a,10 a以上4個(gè)水平,分別用γ1~γ4表示. 按照這3種風(fēng)險(xiǎn)因素,可以將保單持有人分為128個(gè)風(fēng)險(xiǎn)單元,用Yi表示第i個(gè)風(fēng)險(xiǎn)單元的索賠次數(shù).設(shè)Yi服從于NB(μi,r),i=1,2,…,128.Yi之間相互獨(dú)立,采用對數(shù)聯(lián)結(jié)函數(shù)建立的廣義線性模型為 式中:Xi=(xi,1,xi,2,…,xi,18)′;β=(μ0;μ1;α1,…,α8;β1,…,β4;γ1,…,γ4)′;μ0為截距;μ1為索賠額的對數(shù)值.采用SAS軟件的GENMOD過程編程計(jì)算,所得結(jié)果算法收斂. 表1 3種風(fēng)險(xiǎn)因素影響下的索賠額和索賠次數(shù)Tab.1 Number and amount of claims in three risk factors GENMOD過程的第3型分析表明,PA,CG,VA的自由度分別是7,3,3,卡方值分別為150.07, 107.64,119.32,而其顯著性水平p值均小于0.000 1.由此可知,在決定投保人的索賠行為時(shí),3種因素都是非常顯著的. 從評價(jià)擬合優(yōu)度的標(biāo)準(zhǔn)可知,3種因素自由度都為109,但NB分布相對于Poisson分布具有更小的離差和平均離差(NB分布分別為131.732 7,1.208 6,而Poisson分布分別為1 107.793 5,10.163 2).因此,與Poisson分布相比,用NB分布來擬合數(shù)據(jù),其擬合程度更好.參數(shù)估計(jì)的結(jié)果,如表2所示. 從表2可以看出,從保單持有者年齡來說,年齡在40~49歲的人風(fēng)險(xiǎn)最大;而處于17~20歲年齡階段的人風(fēng)險(xiǎn)最小.這里的風(fēng)險(xiǎn)是相對于索賠次數(shù)而言.由此可以說明,17~20歲年齡階段的投保人索賠頻率不高,當(dāng)然,索賠額則不一定了.從車型來看,A,B,C,D等4種車型中,車型B風(fēng)險(xiǎn)最大,而車型D風(fēng)險(xiǎn)最小.從車齡來看,0~3 a的車風(fēng)險(xiǎn)最大,而10 a以上的車風(fēng)險(xiǎn)最小.分析原因應(yīng)該是與新車駕駛員的車技和心理等因素有關(guān),而老車駕駛員相對更重視安全.此外,從表中的Wald卡方統(tǒng)計(jì)量和顯著性水平p值可以看出,所檢驗(yàn)的參數(shù)對于模型基本都是顯著的. 表2 參數(shù)估計(jì)的結(jié)果Tab.2 Analysis of parameter estimates [1]SUSANNE G,CLAUD IA C.Model ling count data with over dispersion and spatial effects[J].Statistical Papers, 2008,49(3):531-552. [2]田霆,劉次華.定時(shí)截尾缺失數(shù)據(jù)下指數(shù)分布的參數(shù)AMLE[J].華僑大學(xué)學(xué)報(bào):自然科學(xué)版,2006,27(4):351-353. [3]FAHRM EIR L,THTZ G.Multivariate statistical model ling based on generalized linear models[M].2nd ed.New York:Sp ringer-Verlag,1996. [4]毛澤春,劉錦萼.一類索賠次數(shù)的回歸模型及其在風(fēng)險(xiǎn)分級中的應(yīng)用[J].應(yīng)用概率統(tǒng)計(jì),2004,20(4):359-367. [5]MCCULLAGH P,NELDER J A.Generalized linear models[M].2nd ed.London:Chapman and Hall,1989. (責(zé)任編輯:陳志賢英文審校:張金順,黃心中) Generalized Linear Model Based on Negative Binomial Distribution and Its Application CHEN Zhuo-heng The properties of the negative binomial distribution which is over-dispersion is discussed in the paper.A generalized linear model which based on the distribution is in truduced.The maximum likelihood estimates and wald test for the model are considered.A t last the model is applied to a real data set of aggregate claims for automobile insurance using SAS package. negative binomial distribution;generalized linear model;wald test;risk classification O 212;F 84 A 1000-5013(2011)02-0226-05 2009-04-14 陳卓恒(1980-),女,講師,主要從事金融統(tǒng)計(jì)和保險(xiǎn)精算方向的研究.E-mail:ranic@163.com. 華僑大學(xué)科研基金資助項(xiàng)目(07HZR04)
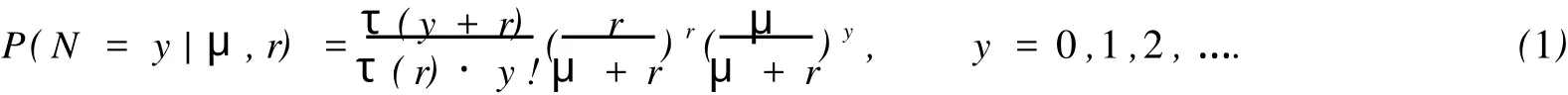
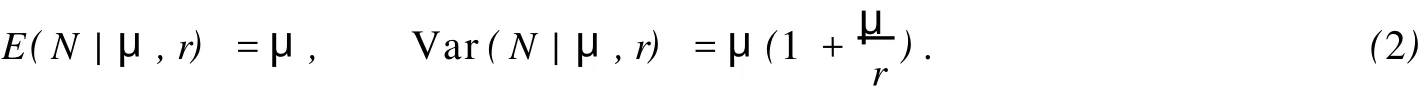
2 廣義線性模型
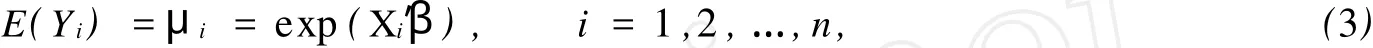
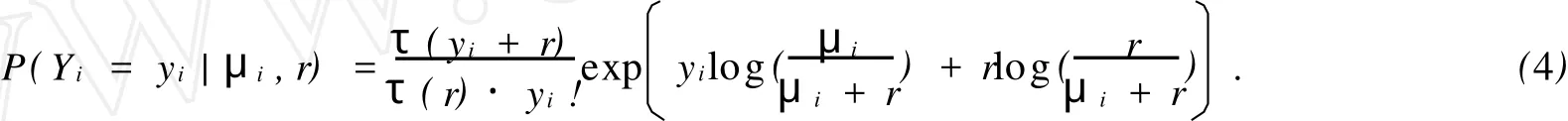

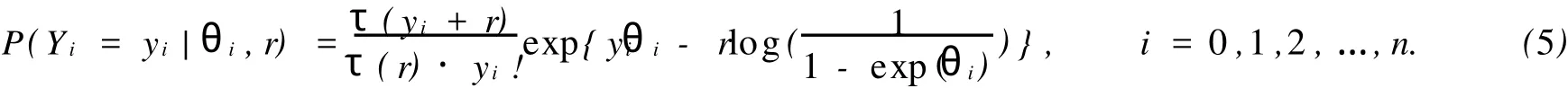

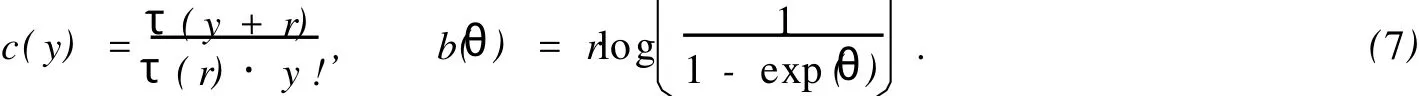
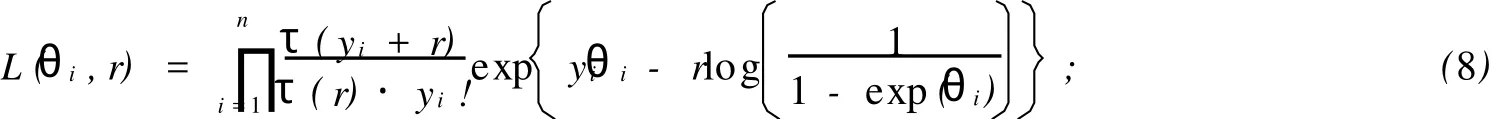
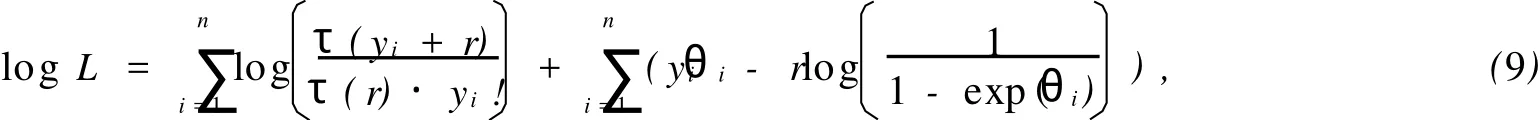
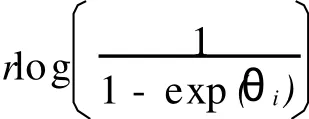
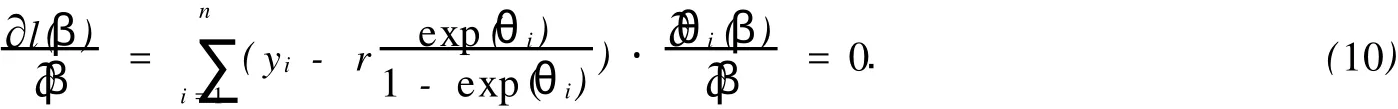

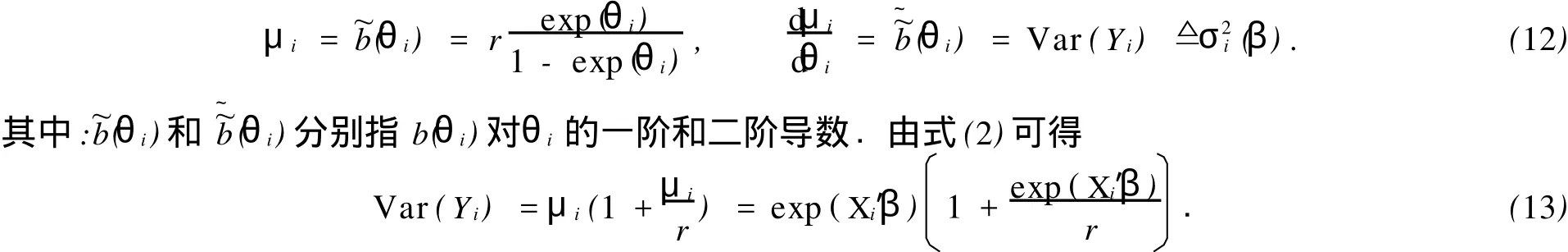

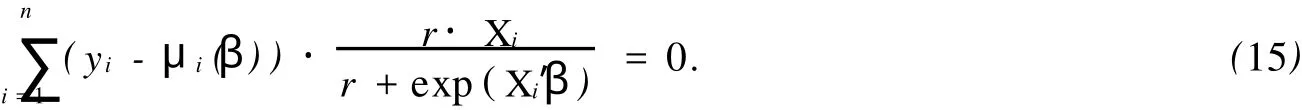
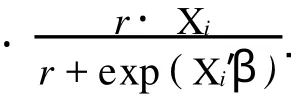





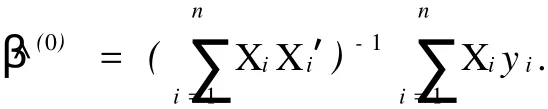
3 實(shí)例分析
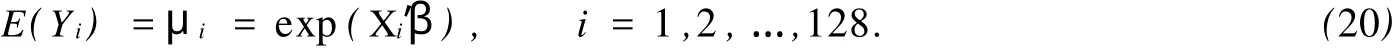

(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

