Chen Fuyang,Jiang Bin,Tao Gang

(1.Collegeof Automation Engineering,NUAA,29 Yudao Street,Nanjing,210016,P.R.China;2.Department of Electrical and Computer Engineering,University of Virginia,Charlottesville,V A 22903,USA)

INTRODUCTION

Helicopters have many merits,such as not relying on the working conditions of the ground,the hovering, small flying-off and landing spaces[1],etc.However,a helicopter is a nonlinear,strong coupling,time-varying complex system with lots of uncertainties[2]. The adaptive controller is designed to control roll attitude[3]and the neural network is used to achieve attitude control on a tilt rotor helicopter rig[4].A helicopter flight control law is designed using a learning control approach[5].

There are many actuator faults and external disturbance in the flight control systems of helicopter.The systems have many moving parts.Fault diagnosis and isolation[6]are more complex,so it is necessary to study the self-repairing capability of the flight control system.The self-repairing control law is usually designed based on the fault detection[7-8].Meanwhile,it is a very difficult work to maintain the quick fault detection and the accurate control precision.Direct self-repairing control can achieve the self-repairing task without the fault diagnosis information[9-11],but has not been reported for a linear varying-parameter helicopter.

In recent years, quantum control technique[12-13]has increasingly been a hot research topic.The quantum evolutionary algorithm maintains a good balance between the coarse search and the strong search,so it has very good collaborative search capabilities and strong global search ability[14-16].The results about the self-repair control using quantum control technology have not been reported yet.

A direct adaptivecontrol approach is presented for the faulty helicopter control system using the fuzzy logic technique,but the external disturbance input is not considered[17].In this paper,the model reference adaptive control law is designed and an adaptive compensator is used for improving its self-repairing capability.Furthermore,quantum control feedforward between fault and disturbance is added to increase the self-repairing control accuracy of helicopter in fault case.Simulation results illustrate the effectiveness and feasibility of the approach.

1 MATHEMATICAL MODEL

The linear varying-parameter model[18]of helicopter is described by

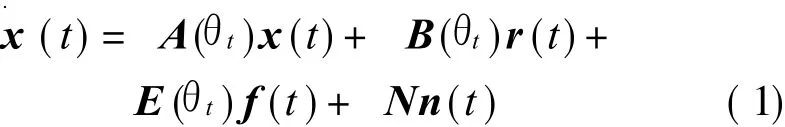
where r(t)=[rcol,rlon]is the control variable of helicopter,r col and r lon are the total distance variable and the longitudinal periodic variable,respectively;x(t)=[u,w,q,θ]is the state variable,u and w are the horizontal and the vertical components,respectively,q is the pitch rate andθ the pitch angle;And A(θt)=

where the parameter vector θt=[θt1,θt2,θt3]is changing associated with the flight speed.When the speed is changed from 60 Kn to 135 Kn(1 Kn? 0.514 m/s),θt1∈ [0.066 4 0.504 7],θt2∈[0.119 8 2.523 0], θt3∈ [0.977 5 5.112 0];E(θt)is the transfer function matrix of injecting actuator fault of helicopter and E(θt)=B(θt);f(t)is the actuator fault of helicopter,N∈ R4×1theorder weighted matrix and n(t)the unknown interference.

The control system is unstable and the state feedback matrix K is used to make the control system stable[17],shown as

K=

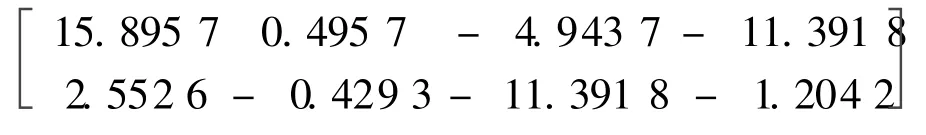
2 DIRECT SELF-REPAIRING CONTROL

2.1 Model ref erence adaptive control

The flight quality of helicopter is worse when a fault occurs.When the model referenceadaptive control law is designed,the flight control system has a strong self-repairing capability and good tracking performance,but it is still bad in horizontal speed and pitch angle.It cannot meet the requirement of the desired flight performance.In order to improve the flight control performance in faulty case,the model reference adaptive control approach for faulty helicopter is proposed using the outer loop adaptive compensation.The overall control structure is depicted in Fig.1.The model reference adaptive controller is designed by Lyapunov′s stability theory and the adaptive compensator is compensated separately by horizontal speed and pitch.

Fig.1 Direct self-repairing control structure of helicopter

Suppose reference model is

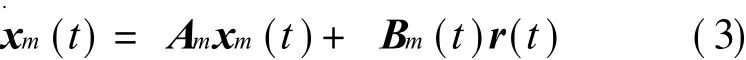
where A m∈ Rn×n,B m∈ Rm×m,C m∈ Rn×n.

The output response of the reference model is presentation of the desired output response of the helicopter control system when the given input is r(t).The generalized error is

In order to compensate changing parameters of helicopter,the feed forward gain matrix K(t)and the feedback gain matrix F(t),which are designed based on Lyapunov′s stability theory,can be shown as

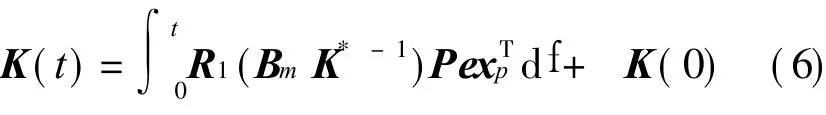
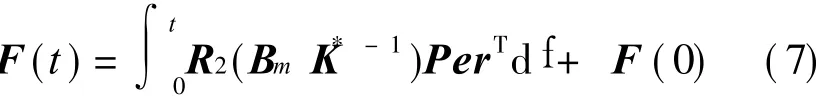
where K(t)∈ Rm×m,F(t)∈ Rm×n,e is the error sig-nal,K*-1the value of K(t)when the helicopter control model perfectly suit to the reference model,P,R1 and R2 are the symmetry positive definite matrixes,K(0)and F(0)the initial values of K(t)and F(t).

The adaptive compensator is designed by equivalent compensator using error signal of horizontal speed and pitch angle.So horizontal speed equivalent compensator is_1,and pitch angle equivalent compensator isθ1[19].where

where K 1,K 2 and a are the undetermined coefficients.So the adaptivecompensator H is

2.2 Quantum control

In quantum computation,|0〉 and|1〉 denote the two basic states of micro-particles,which are named as quantum bit(qubit).Arbitrary qubit state can be expressed as the linear combination of two basic states.The state of qubit not only is|0〉 and|1〉,but also is a linear combination of the state,which is usually called as superposition state,namely

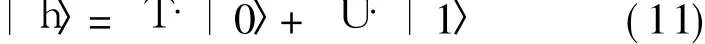
where T and U are a pair of complex,called as the probability amplitude of quantum state.Namely,as the measurement result in quantum state,|h〉collapses|0〉with a probability of|T|2or collapses|1〉with a probability of|U|2.And they satisfy that

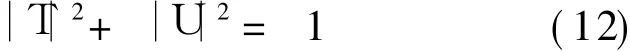
Therefore,quantum state can be also denoted by its probability amplitude in the form of|h〉=[T,U]T.Obviously,when T=1,U=0,|h〉 is the basic state|0〉,which can be described by|h〉=[1,0]T.Otherwise,when T=0,U=1,|h〉is the basic state|1〉,which can be described by|h〉=[0,1]T.Generally speaking,quantum state is theunitvector of two-dimensional complex vector space.

Due to the collapse of quantum states cased by observation,the quantum bit can be seen a continuous state between|0〉 and|1〉,until it has been observed.The existence of continuous state qubit and behavior has been confirmed by a large number of experiments.And the reare many different physical systems can be used to realize quantum bit.

Similarly,three-qubit state can be expressed as

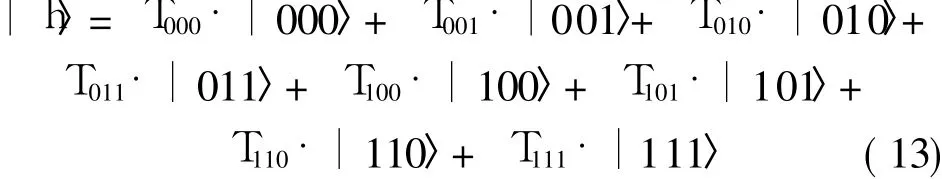
And the probability amplitude satisfies that

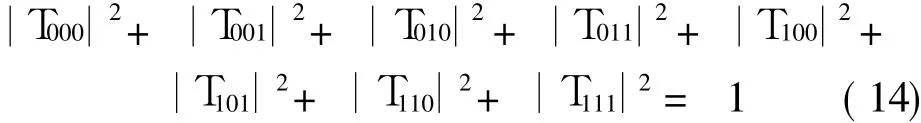
To increase the self-repairing control accuracy of helicopter in fault case,quantum control is added in the approach.The quantum feed forward module in Fig.1 realizes the state description and control of thre equantum bits,and the probability amplitudes of three quantum bits for the module can be seen in Table 1.

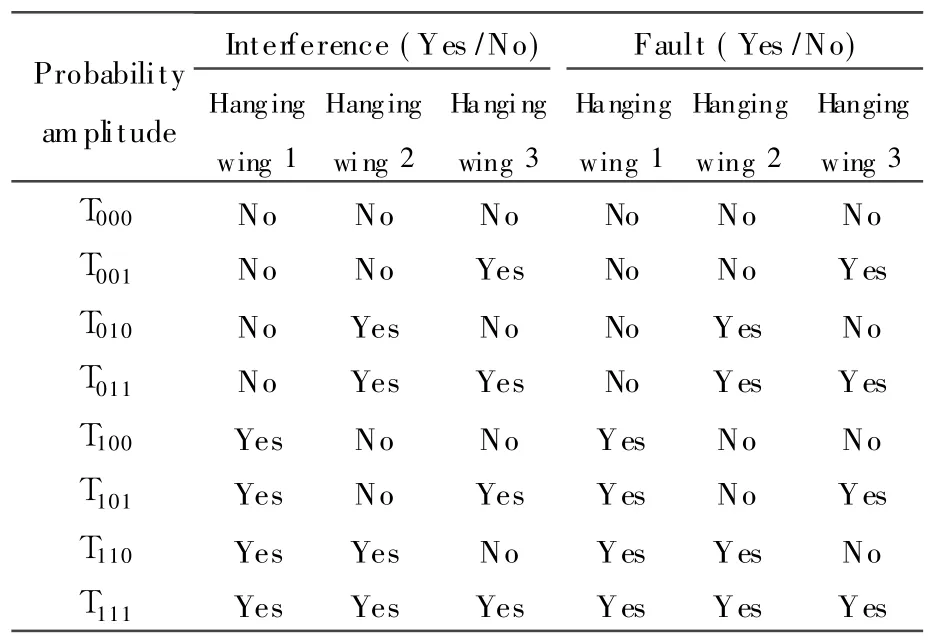
Table 1 Probability amplitudes of three quantum bits for quantum feedforward

3 STABILITY ANALYSIS

The helicopter control system can be transformed into a linear varying-parameter system,so the time-varying state equation can be analyzed.According to Fig.1,the state equation of the faulty helicopter using the outer loop compensation technique can be described as

where

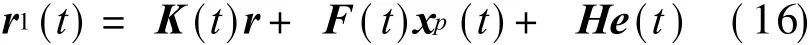
so

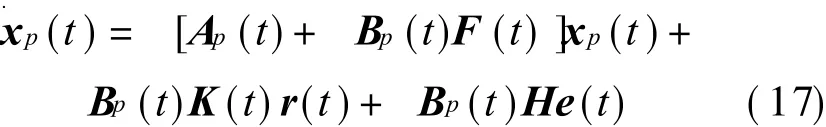
The generalized error state equation can be defined as

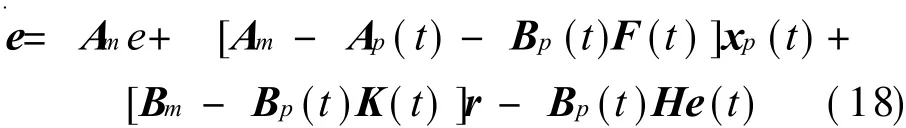
where e is the error signal,A p(t)∈ Rn×n,B p(t)∈Rn×m.The fault can change the elements of the matrix.So the adaptive controller makes regular to K(t)and F(t).It makes thehelicopter control system perfectly suit to the reference model,just as

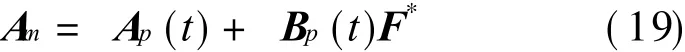
where K*and F*are the values of K(t)and F(t)when the two models are suited perfectly.So Eq.(18)can be described as

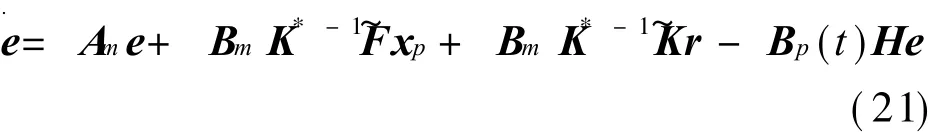
where F~=F*-F(t)is the m×n order matrix,K~=K*-K(t)the m×m order matrix.

Suppose the Lyapunov′function is

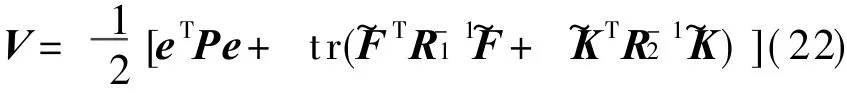
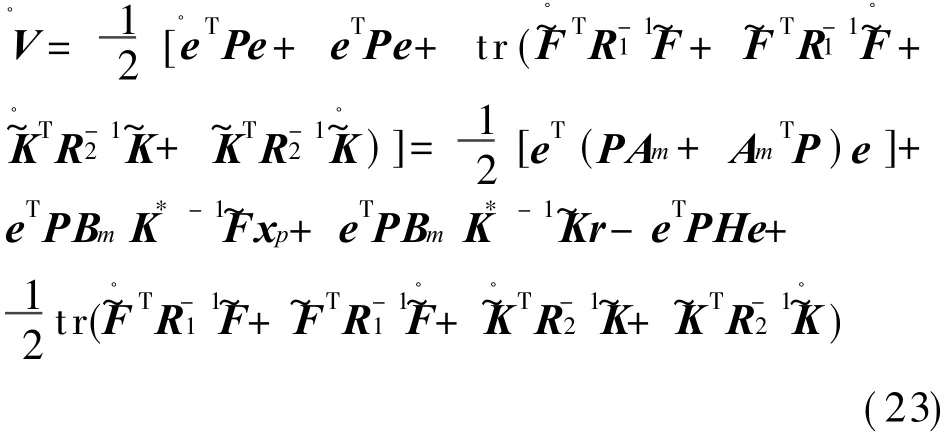
Eq.(23)can be described as

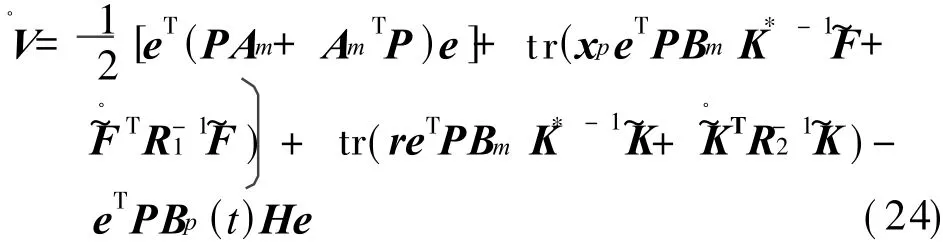
Because of Eqs.(6,7),Eq.(24)can be described as

By Eq.(10),we can get

when K1＞ 0,B p(t)H＞ 0,so?V＜0,which means that the control law can make the control system stable.

4 SIMULATION ANALYSIS

The values of K(t)and F(t)are relevant with R1,R2 and P according to the above derivation.Suppose R1,R2 and P are unit matrixes.In Eqs.(8,9),K(0)=0,F(0)=0;K1=4,K2=50,a=20.The simulation time is 40 s,the reference input is r=[5 5].The approach based on the model reference adaptive control of outer loop compensation helicopter is validated by injecting fault into helicopter in the paper.Suppose some complex faults are worse and worse with time,and can be described as

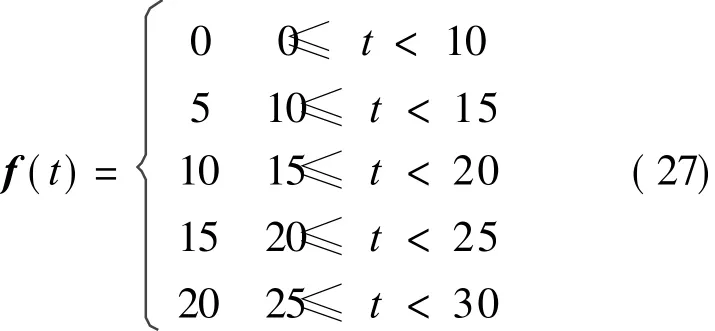
Suppose some strong interferences are described as

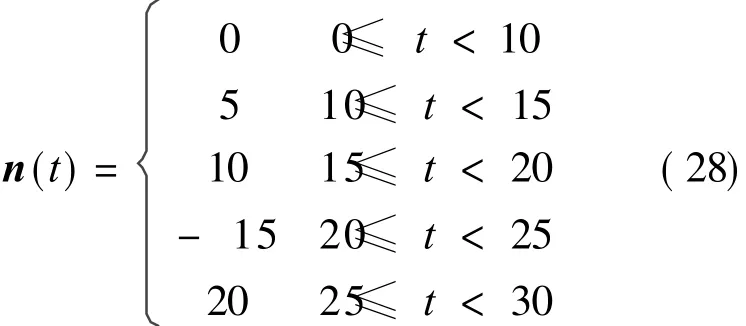
In this paper,the simulation results are shown in Fig.2,where the curve 1 indicates the model referenceoutput;Thecurve 2 indicates the output of the helicopter control system using the model reference adaptive control of helicopter with fault;The curve 3 indicates the output of the helicopter control system without interference,using direct adaptive control of helicopter with fault on the outer loop compensation;The curve 4 indicates theoutput of the helicopter control system with interference,using direct adaptive control of helicopter with fault on the outer loop compensation and quantum control feedforward.

From the simulation,the control quality of helicopter using the model reference adaptivecontrol method is not so good.There are steady state errors.However,direct self-repairing control via quantum control and adaptive compensator makes the helicopter control system have stronger selfrepairing and anti-interference capabilities.

5 CONCLUSION

In this paper,a direct self-repairing control approach is proposed for the faulty helicopter control system by using outer-loop compensation and quantum control feed forward. The approach makes the outputs of the system track asymptotically the outputs of reference model without steady-state error.It is proved that the approach has stronger self-repairing and anti-interference capabilities.

[1] Li Linhua,Hu Qiyuan,Lai Shuiqing.The future development of the helicopter control system in china[J].Helicopter Technique,2007,149(1):55-57.(in Chinese)

[2] Boris A,Fradkov L A,Dimitri P.Adaptive control experiments for LAAS ″Helicopter″ benchmark[C]//International Conference on Physics and Control.St. Petersburg,Russian Federation:[s.n],2005:760-765.

[3] Dzul A,Lozano R,Castillo I P.Adaptive altitude control for a small helicopter in a vertical flying stand[C]//Proceedings of the42nd IEEEConference on Decision and Control Maul.Hawaii,USA:IEEE,2003,12:2710-2715.

[4] Galindo R,Lozano R.Control of under-actuated systems,application to a tandem fan in 3-dof platform[C]//Proceeding of the IEEE International Conference on Control Applications. Anchorage,Alaska,USA:IEEE,2000:25-27.

[5] Enns R,Si J.Helicopter flight control design using a learning control approach[C]//Proceedings of the 39& IEEE Conference on Decision and Control.Sydney,Australia:[s.n.],2000:1754-1759.

[6] Jiang Bin,Chowdhury F N.Fault estimation and accommodation for linear MIMO discrete-time systems[J].IEEE Trans on Control Systems Technology,2005,13(3):493-499.

[7] Elgersma M,Glavaski S.Reconfigurable control for active management of aircraft system failures[C]//Proceedings of the American Control Conference.Arlington,VA:IEEE,2001:2627-2639.

[8] Drozeski G R,Saha B,Vachtsevanos G J.A fault detection and reconfigurable control architecture for unmanned aerial vehicles[C]//IEEE Aerospace Conference.USA:IEEE,2005:2955-2963.

[9] Qi Xiaohui, Yang Zhijun,Wu Xiaoben. Survey study of self-repairing flight control system on UAV[J].Control Engineering of China,2006,13(6):513-516,549.(in Chinese)

[10]Chen Fuyang,Jiang Bin,Zhang Ke.The integrated application on adaptive control of unmanned combat aerial vehicles[C]//Proc of the 2nd International Symposium on Systems and Control in Aeronautics and Astronautics(ISSCAA). Shenzhen,China:[s.n.],2008:1311-1315.

[11]Chen Fuyang,Jiang Bin,Zhang Ke.Direct self-repair control and actuator failures re-present techniques for civil aviation air craft[J].International Journal of Innovative Computing,Information and Control,2009,5(2):503-510.

[12]Chen Zonghai,Dong Daoyi,Zhang Chenbin.Quantum control theory[M].Hefei:University of Scienceand Technology of China Press,2005.(in Chinese)

[13]Cong Shuang,Zheng Yisong,Ji Beichen,et al.Survey of progress in quantum control system[J].Chinese Journal of Quantum Electronica,2003,20(1):1-9.(in Chinese)

[14]Han K H,Kim J H.Genetic quantum algorithm and its application to combinational optimization problem[C]//Proceedings of the International Congress on Evolutionary Computation.Piscataway,N J:IEEE Press,2000:1354-1360.

[15]Li Shiyong,Li Panchi.Quantum computation and quantum optimization algorithms[M]. Harbin:Harbin In stituteof Technology Press,2009.(in Chinese)

[16]Dong D Y,Chen C L,Tarn T J,et al.Incoherent control of quantum systems with wavefunction controllable subspaces via quantum reinforcement learning[J].IEEE Transactions on Systems,Man,and Cybernetics,2008,38(4):957-962.

[17]Chen Fuyang,Jiang Bin,Liu Yuhang.Direct selfadapting control of faulty helicopter based on fuzzy logic[J].Huazhong Univ of Sci&Tech:Natural Science Edition,2009,37(SⅠ):131-134.(in Chinese)

[18]Chen Wei,Jiang Bin,Zhang Ke,et al.Robust fault diagnosis for helicopter FCSbased on linear parameter-varying adaptive observer[J].Transactions of Nanjing University of Aeronautics and Astronautics,2009,26(4):288-294.

[19]Kong Wei,Gu Lina,Yu Fei.Function of integration in improving precision of fuzzy controller[J].Journal of Qingdao Institute of Chemical Technology,2001,22(1):66-68.(in Chinese)