呂家鳳, 包科維, 葉曉曉, 王一帆

(浙江師范大學(xué)數(shù)理與信息工程學(xué)院,浙江金華 321004)

0 引 言

Koszul代數(shù)最初由 Priddy[1]提出,它是一類具有許多優(yōu)美同調(diào)性質(zhì)且在數(shù)學(xué)的諸多分支均有重要應(yīng)用的二次代數(shù).Berger[2]首次把這類代數(shù)推廣到高次代數(shù)上,引入了非二次的 Koszul代數(shù),這類代數(shù)后來常被稱為 D-Koszul代數(shù)[3-4].Green等[5]把 Koszul對象推廣到非分次情形,討論了諾特半完全代數(shù)的 Koszul性質(zhì)和諾特半完全代數(shù)上的有限生成模的 Koszul性質(zhì),定義了擬 Koszul代數(shù)和擬 Koszul模.受文獻(xiàn)[5]的啟發(fā),文獻(xiàn)[6]研究了諾特半完全代數(shù)的D-Koszul性質(zhì),引入了擬 D-Koszul代數(shù)的概念;文獻(xiàn)[7-8]討論了諾特半完全代數(shù)上的有限生成模的 D-Koszul性質(zhì),定義了擬 D-Koszul模.而 Koszul-like代數(shù)和 Koszul-like模是 Koszul代數(shù)和 Koszul模的又一自然推廣 (事實上,Koszul代數(shù)到目前為止已經(jīng)有很多形式的推廣,如文獻(xiàn)[9-12]),且有例子表明,某些整體維數(shù)是 5的 Artin-Schelter正則代數(shù)是 Kos-zul-like代數(shù).

本文主要把 Koszul-like模推廣到非分次情形,討論了諾特半完全代數(shù)上有限生成模的 Koszul-like性質(zhì),定義了擬 Koszul-like模,并試圖把有關(guān) Koszul-like模的一些好的性質(zhì)推廣到非分次情形.

1 Koszul-like模及其極小分次投射分解

其中,d,t1和 t2是滿足 d>t2>t1>1的自然數(shù).

定義 1 設(shè) A是標(biāo)準(zhǔn)分次代數(shù).稱有限生成分次 A-模M為 Koszul-like模,如果 A-模 M有極小分次投射解

使得對于任意的 n≥0,Pn由δdt1,t2(n)次生成.特別地,若平凡 A-模 A0是 Koszul-like模,則稱標(biāo)準(zhǔn)分次代數(shù) A是 Koszul-like代數(shù).

顯然,對于 Koszul-like模,有如下判定方法:

命題 1 設(shè)A是標(biāo)準(zhǔn)分次代數(shù),M是有限生成的非負(fù)分次A-模,則M是 Koszul-like模當(dāng)且僅當(dāng)對任

證明 類似于λ-Koszul模[11]的情形,故略.

命題 2[5]設(shè)A是標(biāo)準(zhǔn)分次代數(shù),則存在有限箭向圖Γ和路代數(shù) kΓ的分次理想 I?∑n≥2(kΓ)n,使得作為分次代數(shù),有 A?kΓ/I成立.

定理 1 設(shè) A=kΓ/I是標(biāo)準(zhǔn)分次代數(shù),M是由 0次生成的分次 A-模.設(shè)

是 A-模M的極小分次投射分解,則M是由δdt1,t2定義的 Koszul-like模當(dāng)且僅當(dāng)對任意 n≥0,有 kerdn?

t1,t2(n+1)次生成矛盾.因此,x∈Jkerdn.

定義 2 設(shè) R是諾特半完全代數(shù),J是其 Jacobson根,M是有限生成的 R-模,則稱M是擬 Koszul-like模當(dāng)且僅當(dāng)M有極小投射解

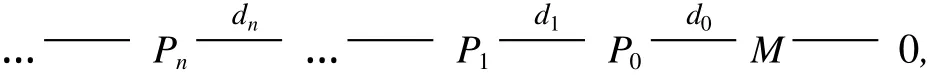
使得對任意的 n≥0,有

特別地,若 R/J是擬 Koszul-like模,則稱 R是擬 Koszul-like代數(shù).

例 1 1)局部正則代數(shù)[13]是擬 Koszul-like代數(shù).事實上,令 R是局部正則代數(shù),m是 R的極大理想,且 G(R)=n.設(shè) x1,x2,…,xn是 R的一正則序列.通過常規(guī)計算,平凡模 R/m有如下極小投射分解:

其中 e1,e2,…,en是 R⊕n的一組自由基.不難驗證 R是擬 Koszul-like代數(shù).

2)Green等在文獻(xiàn) [5]中定義的擬 Koszul代數(shù) (模)是義的擬 Koszul-like代數(shù) (模).

2 諾特半完全代數(shù)上的有限生成模

本節(jié)主要回顧諾特半完全代數(shù)上的有限生成模的基本性質(zhì),其中絕大部分內(nèi)容可在文獻(xiàn)[8]中找到,由于它在本文中具有重要作用,因此給出簡要敘述.采用文獻(xiàn)[8]中的記號,設(shè) R是諾特半完全代數(shù),J是 R的 Jacobson根,則對任意有限生成的 R-模M,必有如下投射分解:

使得對任意的 n≥0,Qn是有限生成的 R-模且 kerfn?JQn,即分解 Q是“極小的”.為簡潔起見,記 Si:=kerfi-1,常稱 Si為 M的第 i個合沖.記

在 Yoneda積下,E(R)是分次代數(shù),ε(M)作成分次 E(R)-模.值得注意的是,在本節(jié)的情形下,它們都不再是雙分次的.然而,可以在ε(M)上定義第二次數(shù)

引理 1[8]采用上述記號,有下列命題成立:

引理 2[8]設(shè) R是諾特半完全代數(shù),M是有限生成的 R-模,且

是M的極小投射解.令 f:N→N為任意一個滿足 f(i)≥i≥1的遞增的集合映射.則

3 擬 Koszul-like模的 Ext模

本節(jié)主要討論如何用 Ext模刻畫擬 Koszul-like模.

因此,對任意的 i≥1,δdt1,t2(i-1)=i-1,即M是擬 Koszul模.命題 3證畢.

注 1 命題 3表明,對于擬 Koszul-like模,沒有類似于命題 1的結(jié)論,但仍然可以通過 Ext-模的第二次數(shù)刻畫擬 Koszul-like的性質(zhì).

定理 2 設(shè) R是諾特半完全代數(shù),M是有限生成的 R-模,則M是擬 Koszul-like模當(dāng)且僅當(dāng)對任意的 i≥1,有

證明 必要性 設(shè)M是擬 Koszul-like模且

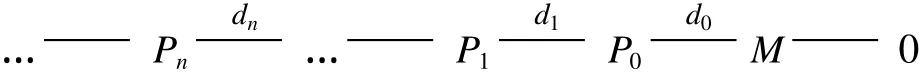
是M的極小投射分解.采用前面的記號 Si:=kerdi-1,則根據(jù)擬 Koszul-like模的定義,對任意的 i≥1,

即M是擬 Koszul-like模.定理 2證畢.

定理 3 設(shè) R是諾特半完全代數(shù),M是有限生成的 R-模.若有下列條件成立:

則M是擬 Koszul-like模.

綜上,定理 3得證.

[1]Priddy S B.Koszul resolutions[J].TransAmerMath Soc,1970,152:39-60.

[2]Berger R.Koszulity for nonquadratic algebras[J].J Alg,2001,239(2):705-734.

[3]Green E L,Marcos E,Martínez-Villa R,et al.D-Koszul algebras[J].J Pure ApplAlg,2004,193(1/2/3):141-162.

[4]Cheng Zhi,Ye Yu.One-point extensions oft-Koszul algebras[J].ActaMath Sin:Engl Ser,2007,23(6):965-972.

[5]Green E L,Martínez-Villa R.Koszul and Yoneda-Ext algebras[J].Conference Proc AMS,1996,18:247-297.

[6]He Jiwei,Ye Yu.On the Yoneda-Ext algebras of semiperfect algebras[J].Alg Colloq,2008,15(2):207-222.

[7]呂家鳳,冷雁.擬 d-Koszul模[J].浙江大學(xué)學(xué)報:理學(xué)版,2008,35(5):481-485.

[8]司君如.高階擬 Koszul模[J].數(shù)學(xué)學(xué)報,2009,55(5):101-110.

[9]LüJiafeng.On moduleswithd-Koszul-type submodules[J].ActaMath Sin:Engl Ser,2009,25(6):1015-1030.

[10]LüJiafeng.On moduleswith piecewise-Koszul towers[J].Houston J Math,2009,35(1):187-205.

[11]LüJiafeng.Algebraswith periodic shifts of Ext degrees[J].Math Notes,2009,86(5/6):665-681.

[12]LüJiafeng,He Jiwei,Lu Diming.Piecewise-Koszul algebras[J].Sci China:A,2007,50(12):1795-1804.

[13]Weibel C A.An Introduction to HomologicalAlgebra[M].Cambridge:Cambridge Univ Press,1995.