張 麗,趙良煦,王壽光,汪成英

(浙江工商大學(xué)信息與電子工程學(xué)院,浙江杭州 310018)

針對(duì)α網(wǎng)的最優(yōu)線性約束轉(zhuǎn)換方法

張 麗,趙良煦,王壽光,汪成英

(浙江工商大學(xué)信息與電子工程學(xué)院,浙江杭州 310018)

針對(duì)不可控影響子網(wǎng)為α網(wǎng)的一類(lèi)Petri網(wǎng),提出了將給定的廣義互斥約束轉(zhuǎn)換成最優(yōu)允許線性約束的方法.該方法首先獲得了該網(wǎng)的不可控影響子網(wǎng);其次,提出了轉(zhuǎn)換后的禁止庫(kù)所集集合的求解算法;最后,根據(jù)禁止庫(kù)所集集合構(gòu)造了“邏輯或”形式的最大允許線性約束.并且通過(guò)一個(gè)例子,說(shuō)明了該方法的有效性.

Petri網(wǎng);離散事件系統(tǒng);禁止?fàn)顟B(tài);不可控變遷

在離散事件系統(tǒng)中,監(jiān)控系統(tǒng)行為使其不進(jìn)入禁止?fàn)顟B(tài)并滿(mǎn)足系統(tǒng)的性能要求是極其重要的.但是如何控制系統(tǒng)行為,避免其進(jìn)入禁止?fàn)顟B(tài)是一個(gè)非常棘手的問(wèn)題.此類(lèi)控制問(wèn)題可以用線性約束方法來(lái)表示.在基于Petri網(wǎng)的離散事件系統(tǒng)監(jiān)控器設(shè)計(jì)[1-14]中,線性約束轉(zhuǎn)換問(wèn)題一直是研究的重點(diǎn).當(dāng)Petri網(wǎng)的所有變遷都可控時(shí),可以直接設(shè)計(jì)最優(yōu)控制器[1].但當(dāng)網(wǎng)中存在不可控變遷時(shí),根據(jù)給定的線性約束限制系統(tǒng)的行為是不夠的.這是因?yàn)椴豢煽刈冞w的實(shí)施會(huì)導(dǎo)致合法標(biāo)識(shí)集的某些狀態(tài)演變成禁止?fàn)顟B(tài),即不再滿(mǎn)足給定的約束,致使系統(tǒng)無(wú)法滿(mǎn)足性能要求.因此,需通過(guò)線性約束轉(zhuǎn)換方法得到最優(yōu)允許標(biāo)識(shí)集,使得限制系統(tǒng)行為在允許標(biāo)識(shí)集中,從而避免系統(tǒng)進(jìn)入禁止?fàn)顟B(tài).目前,如何通過(guò)線性約束轉(zhuǎn)換得到允許標(biāo)識(shí)集仍是一大難題.

針對(duì)含有不可控變遷的Petri網(wǎng)的線性約束轉(zhuǎn)換研究,文獻(xiàn)[2-4]提出了基于關(guān)聯(lián)矩陣運(yùn)算的線性約束轉(zhuǎn)換方法,但是轉(zhuǎn)換后的線性約束僅僅表示了允許標(biāo)識(shí)集的一個(gè)子集,即無(wú)法保證監(jiān)控器的最大允許性.文獻(xiàn)[5-6]在Moody提出的算法上進(jìn)一步研究了約束轉(zhuǎn)換方法且提高轉(zhuǎn)換效率,但是最終得到的約束仍不是最優(yōu)解.文獻(xiàn)[7]針對(duì)一類(lèi)子網(wǎng)提出了將給定的線性約束轉(zhuǎn)換的允許線性約束的方法,但該方法計(jì)算效率不高.文獻(xiàn)[8]提出了自下而上的約束轉(zhuǎn)換的方法,該方法計(jì)算效率高,但是針對(duì)的是Petri網(wǎng)中不可控變遷只有1個(gè)輸入庫(kù)所的情況.對(duì)于不可控變遷有多個(gè)輸入庫(kù)所的情況,文獻(xiàn)[9]提出了用“邏輯或”形式的線性約束來(lái)表示允許標(biāo)識(shí)集的算法,但是該方法得到的約束并不是最大允許.此外,文獻(xiàn)[9]沒(méi)有準(zhǔn)確地定義允許標(biāo)識(shí)集這個(gè)概念,因此,約束轉(zhuǎn)換問(wèn)題仍然沒(méi)有得到解決.所以,文中針對(duì)一類(lèi)網(wǎng)研究此類(lèi)問(wèn)題.

筆者主要針對(duì)Petri網(wǎng)的某一類(lèi)子網(wǎng)的線性約束轉(zhuǎn)換問(wèn)題進(jìn)行深入研究,提出了求解最大允許線性約束的方法.該方法首先根據(jù)定義獲得不可控影響子網(wǎng);其次,提出了求解轉(zhuǎn)換后禁止庫(kù)所集集合的算法;最后,根據(jù)禁止庫(kù)所集集合構(gòu)造了“邏輯或”形式的最大允許線性約束.筆者主要針對(duì)不可控變遷存在多個(gè)輸入庫(kù)所的Petri網(wǎng)的某一類(lèi)子網(wǎng)來(lái)進(jìn)行研究,提出了最優(yōu)線性約束轉(zhuǎn)換的算法,使得系統(tǒng)監(jiān)控達(dá)到了最優(yōu)控制.

1 基礎(chǔ)知識(shí)

1.1 Petri網(wǎng)

一個(gè)普通Petri網(wǎng)N是一個(gè)四元組(P,T,F,m0),P和T分別稱(chēng)為庫(kù)所和變遷的集合.P和T非空,有限且不相交.也就是說(shuō),P≠?,T≠?,P∩T=?.F?(P×T)∪(T×P)稱(chēng)為流關(guān)系或是有向弧的集合.令x∈P∪T是Petri網(wǎng)N=(P,T,F)的節(jié)點(diǎn).x的前置集x定義為x={y∈P∪T|(y,x)∈F},x的后置集x定義為x= {y∈P∪T|(x,y)∈F}.令X?P∪T是節(jié)點(diǎn)的集合,X的前置集定義為·X=的后置集定義為N的關(guān)聯(lián)矩陣N是一個(gè)以P×T為序標(biāo)的整數(shù)矩陣.如果p是t的前置,則N(p,t)=-1;如果p是t的后置,則N(p,t)=1.則對(duì)于剩下的其他p和t,N(p,t)=0.庫(kù)所p對(duì)應(yīng)的行向量稱(chēng)為p的關(guān)聯(lián)向量,記做N(p,).變遷t對(duì)應(yīng)的列向量稱(chēng)為t的關(guān)聯(lián)向量,記做N(,t).

Petri網(wǎng)N=(P,T,F)的標(biāo)識(shí)m是一個(gè)從P到N={0,1,2,…}的映射.(N,m0)稱(chēng)為網(wǎng)系統(tǒng)或標(biāo)識(shí)網(wǎng),m0稱(chēng)為N的初始標(biāo)識(shí).一般地,用多集合符號(hào)p來(lái)表示m,其中,m(p)表示m中每一個(gè)庫(kù)所p中的托肯數(shù).稱(chēng)t∈T在標(biāo)識(shí)m下是使能的,當(dāng)且僅當(dāng)?p∈t,m(p)＞0,記為m[t〉.使能的變遷可以發(fā)射.變遷t發(fā)射后,網(wǎng)系統(tǒng)躍遷到另一個(gè)狀態(tài),產(chǎn)生一個(gè)新的標(biāo)識(shí)m′,使得?p∈P,m′(p)=m(p)+N(p, t).在標(biāo)識(shí)m下發(fā)射t到達(dá)標(biāo)識(shí)m′,記為m[t〉m′.稱(chēng)標(biāo)識(shí)m′是從m1可達(dá)的,當(dāng)且僅當(dāng)存在一個(gè)變遷的發(fā)射序列γ=t1,t2,…,tn和標(biāo)識(shí)m1,m2,…,mn,使得m1[t1〉m2[t2〉…mn[tn〉m′成立.在該網(wǎng)中,把從m0可達(dá)的所有標(biāo)識(shí)的集合稱(chēng)為(N,m0)的可達(dá)集,記為R(N,m0).

Petri網(wǎng)中,受外部控制器直接限制的變遷是可控變遷;否則,是不可控的.Tc(Tu)分別表示為可控(不可控)變遷的集合.滿(mǎn)足p=?的庫(kù)所稱(chēng)為匯庫(kù)所,用ps表示.

Petri網(wǎng)的一條路就是它圖中的一條有向路,如果一條路上的所有變遷都是不可控的,則稱(chēng)它為不可控路,一條從可控變遷t到庫(kù)所p的路,如果除t外,其他變遷都是不可控的,則稱(chēng)它為內(nèi)部不可控路.

1.2 線性約束

定義1廣義互斥約束(Generalized Mutual Exclusion Constraint,GMEC)是一個(gè)二元組(w,k),可表示為wm≤k,其中,w是一個(gè)從庫(kù)所集到非負(fù)整數(shù)集上的映射,即w:P→{0,1,2,…},同時(shí)也可看做是一個(gè)1×P的非負(fù)整數(shù)向量,即其第i維上的值wi等于w(pi);k∈N N.文中將廣義互斥約束簡(jiǎn)稱(chēng)為線性約束[3].

為了問(wèn)題的簡(jiǎn)化討論,以下給定的線性約束(w,k)形式都為m(ps)≤k.

定義2給定一個(gè)Petri網(wǎng)系統(tǒng)N=(P,T,F,m0)和一個(gè)廣義互斥約束(w,k),則禁止標(biāo)識(shí)集Mw,k∶= {m∈M|wm＞k},合法標(biāo)識(shí)集Lw,k∶={m∈R(N,m0)|wm≤k},允許標(biāo)識(shí)集Aw,k∶={m∈R(N,m0)| Ru(m)?Lw,k,其中,Ru(m)表示只有不可控變遷發(fā)射下,從m可達(dá)的所有標(biāo)識(shí)的集合.禁止庫(kù)所集Pf∶= {p∈Pw|w(p)≠0}[3].

定義3線性約束不等式集W∶={(w1,k),…,(wn,k)},n∈Z,“邏輯或”形式可表示為∨(W),即.其合法標(biāo)識(shí)集允許標(biāo)識(shí)集A∨(W)∶={m∈R(N,m0)|Ru(m)?

定義4給定一個(gè)Petri網(wǎng)系統(tǒng)N=(P,T,F,m0)和一個(gè)廣義互斥約束(w,k):m(ps)≤k,則該系統(tǒng)的不可控影響子網(wǎng)可表示為Nw∶=(Pw,Tw,Fw),其中,Pw是存在連向ps的不可控路徑的全部庫(kù)所的集合,Tw是包含在連向ps的不可控路徑內(nèi)的全部變遷的集合,Fw=F ∩((Pw×Tw)∪(Tw×Pw))[7].

定義5一個(gè)無(wú)環(huán)普通Petri網(wǎng)N=(P,T,F)稱(chēng)為是α網(wǎng),當(dāng)且僅當(dāng)滿(mǎn)足下列條件:網(wǎng)中有且僅有一個(gè)庫(kù)所沒(méi)有輸出變遷,即只有一個(gè)匯庫(kù)所.每個(gè)變遷有且只有1個(gè)輸出庫(kù)所.每個(gè)庫(kù)所最多只有1個(gè)輸出變遷[7].

2 線性約束轉(zhuǎn)換

2.1 可允許的約束條件

定義6當(dāng)且僅當(dāng)廣義互斥約束(w,k)中所有合法標(biāo)識(shí)都是允許的,則該約束(w,k)是允許約束,即Lw,k?Aw,k[7].

定義7給定一個(gè)廣義互斥約束(w,k)和其允許標(biāo)識(shí)集Aw,k,轉(zhuǎn)換后的“邏輯或”形式的約束∨(W)是最大允許約束,當(dāng)且僅當(dāng)L∨(W)=Aw,k.該轉(zhuǎn)換即為最優(yōu)轉(zhuǎn)換[9].

2.2 最優(yōu)約束轉(zhuǎn)換算法

這里主要針對(duì)不可控影響子網(wǎng)為α網(wǎng)的Petri網(wǎng)進(jìn)行線性約束轉(zhuǎn)換討論.為了簡(jiǎn)化討論,假定給定的線性約束(w,k)形式為m(ps)≤k.顯然,對(duì)于給定的線性約束,在不可控影響子網(wǎng)為α網(wǎng)的情況下,Nw中每個(gè)輸入庫(kù)所在其他庫(kù)所托肯數(shù)足夠多的情況下,經(jīng)過(guò)不可控變遷實(shí)施之后轉(zhuǎn)換的權(quán)值w(p)是一樣的,且都等于w(ps),文中假定w(ps)=1.

根據(jù)前面的定義及討論,提出了將初始線性約束轉(zhuǎn)換成“邏輯或”形式的最大允許線性約束的算法.

算法1線性約束轉(zhuǎn)換.

輸入:一個(gè)Petri網(wǎng)(N,m0),其中,N=(P,Tc∪Tu,F),初始線性約束(w,k):m(ps)≤k.

輸出:W∶={(w1,k),…,(wn,k)},其中,n∈Z.

根據(jù)定義2和4,得到不可控影響子網(wǎng)及禁止庫(kù)所集Pf0={ps}

Ω′∶={Pf0}; //Ω′表示轉(zhuǎn)換前的禁止庫(kù)所集集合

Ω∶=?; //Ω表示轉(zhuǎn)換后的禁止庫(kù)所集集合且初始為空

WHILEΩ′≠?DO //當(dāng)Ω′不為空時(shí),進(jìn)行以下操作

FOR?Pf∈Ω′DO //對(duì)Ω′中任意禁止庫(kù)所集Pf

Ω′∶=Ω′Pf; //除去該禁止庫(kù)所集Pf

FOR?t∈·Pf-Pf·,t∈TuDO

FOR?p∈t DO

B∶=Pf∪{p}; //B表示禁止庫(kù)所集

IF·B-B·=?THEN

Ω∶=Ω∪{B}

ELSE

Ω′∶=Ω′∪{B}

END IF

END FOR

END FOR

END FOR

END WHILE

轉(zhuǎn)換得到Ω={Pf1,…,Pfn}

Ω中每個(gè)Pfi對(duì)應(yīng)的約束(wi,k):

W∶={(w1,k),…,(wn,k)}.

2.3 實(shí) 例

例1已知一個(gè)Petri網(wǎng)N=(P,T,F)如圖1所示,P={p1-p7},Tu={t1-t3},給定初始約束條件是(w,k):m(p1)≤k.

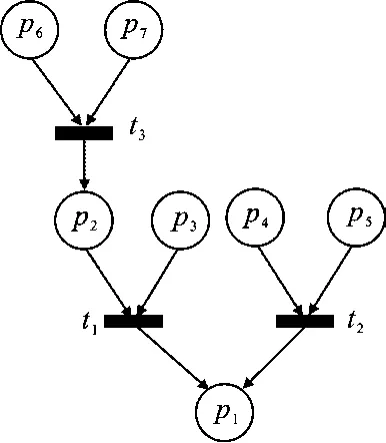
圖1 含有不可控變遷的Petri網(wǎng)

根據(jù)算法1和圖1,初始時(shí)禁止庫(kù)所集集合Ω′={{p1}},Ω=?,由于Ω′≠?,所以對(duì)初始禁止庫(kù)所集Pf0={p1}進(jìn)行轉(zhuǎn)換,經(jīng)過(guò)不可控變遷t1,Pf0轉(zhuǎn)換成了集合B1={p1,p2}與集合B2={p1,p3},因?yàn)椤1-B·1≠?,·B2-B2·≠?,所以Ω′={{p1,p2},{p1,p3}},Ω=?.繼續(xù)判斷得到的Ω′≠?,對(duì)Ω′中的禁止庫(kù)所集進(jìn)行轉(zhuǎn)換.經(jīng)過(guò)不可控變遷t2,原先的B1轉(zhuǎn)變成了B3={p1,p2,p4}和B4={p1,p2,p5},B2轉(zhuǎn)變成了B5={p1,p3,p4}和B6={p1,p3,p5}.因?yàn)椤3-B3·≠?,·B4-B4·≠?,·B5-B5·=?,·B6-B6·=?,所以Ω′={{p1,p2,p4},{p1,p2,p5}},Ω={{p1,p3,p4},{p1,p3,p5}}.經(jīng)過(guò)判斷Ω′仍然不等于空集,繼續(xù)進(jìn)行轉(zhuǎn)換.經(jīng)過(guò)不可控變遷t3,B3轉(zhuǎn)變成B7={p1,p2,p4,p6}和{p1,p2,p4,p7},B4轉(zhuǎn)變成B8={p1,p2,p5,p6}和{p1,p2,p5,p7}.而·B7-B7·=?,·B8-B8·=?,所以Ω′=?,Ω={{p1,p3,p4},{p1,p3,p5},{p1,p2,p4,p6},{p1,p2,p4,p7},{p1,p2,p5,p6},{p1,p2,p5,p7}}.此時(shí),Ω′=?.轉(zhuǎn)換結(jié)束.

其禁止庫(kù)所集集合Ω′與Ω的轉(zhuǎn)變過(guò)程如下:

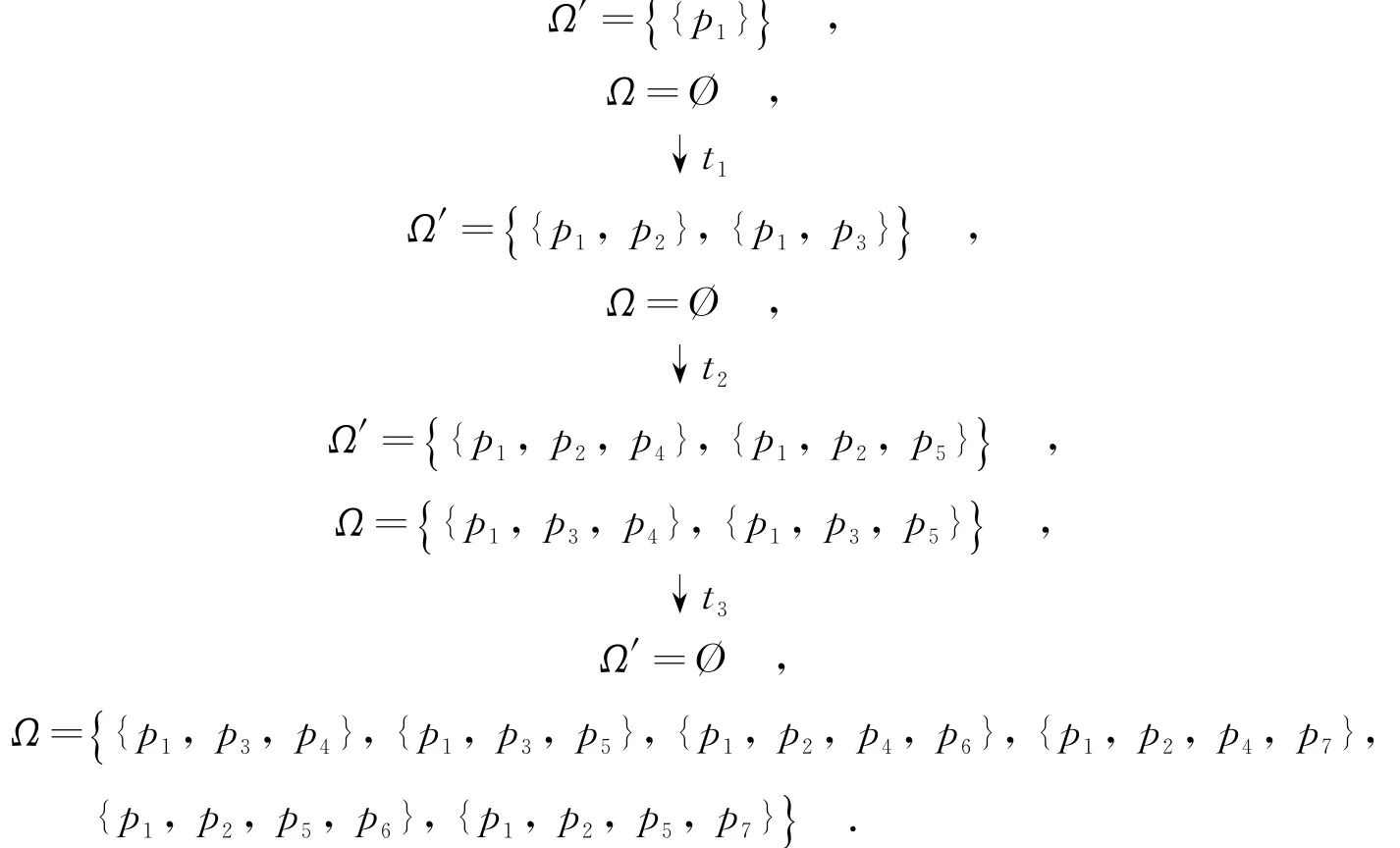
所以禁止庫(kù)所集集合Ω={Pf1,Pf2,Pf3,Pf4,Pf5,Pf6}={{p1,p3,p4},{p1,p3,p5},{p1,p2,p4,p6},{p1,p2,p4,p7},{p1,p2,p5,p6},{p1,p2,p5,p7}}.

因此,原始線性約束轉(zhuǎn)換成:

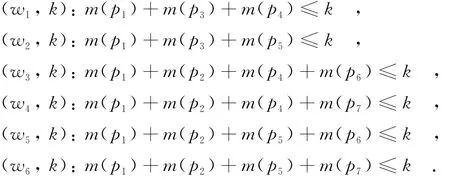
最終,轉(zhuǎn)換后的“邏輯或”形式的約束W={(w1,k),(w2,k),(w3,k),(w4,k),(w5,k),(w6,k)}.

定義8給定一個(gè)Petri網(wǎng)及線性約束(w,k),變遷t的權(quán)值定義為

定理1給定初始廣義約束(w,k),如果不可控影響子網(wǎng)為α網(wǎng),則根據(jù)算法1轉(zhuǎn)換后的“邏輯或”形式的線性約束W={(w1,k),…,(wn,k)}是最大允許的.

證明 根據(jù)定義7,轉(zhuǎn)換后的“邏輯或”形式的線性約束是最大允許的,當(dāng)且僅當(dāng)L∨(W)=Aw,k.因此,證明可從兩部分來(lái)進(jìn)行,L∨(W)=A∨(W)和A∨(W)=Aw,k.假設(shè)tx為網(wǎng)中不可控變遷,tx≠?.

(1)L∨(W)=A∨(W).根據(jù)算法1,初始標(biāo)識(shí)m經(jīng)過(guò)不可控變遷tx的實(shí)施,會(huì)產(chǎn)生最終的新的標(biāo)識(shí)m′,滿(mǎn)足wm′≤k.根據(jù)α網(wǎng)的結(jié)構(gòu)特性,顯而易見(jiàn),此時(shí)不可控變遷tx的再次激發(fā),不會(huì)使wm′的值繼續(xù)增加,即wm′≤wm.也就是,(tx)≤0.由文獻(xiàn)[2]可知,對(duì)于?t∈Tu(t)≤0,則線性約束(w,k)是允許的.因此,轉(zhuǎn)換得到新的線性約束∨(W)都是允許約束,也就是約束中所有合法標(biāo)識(shí)都是允許的,即L∨(W)?A∨(W).根據(jù)定義2和定義3,又得到A∨(W)?L∨(W),所以L∨(W)=A∨(W).

(2)Aw,k=A∨(W).首先,Aw,k?A∨(W),根據(jù)算法轉(zhuǎn)換,對(duì)于W中任意的線性約束(w′,k),都有w′≥w.因此,?(w′,k)∈W,?m,w′m≥wm.顯然,屬于A∨(W)的合法標(biāo)識(shí)必然屬于Aw,k,故Aw,k?A∨(W).

其次,Aw,k?A∨(W).線性約束(w,k)中任一允許標(biāo)識(shí)m經(jīng)過(guò)不可控變遷的實(shí)施,產(chǎn)生的最終標(biāo)識(shí)的最大值定義為由于α網(wǎng)的結(jié)構(gòu)特殊性很顯然,經(jīng)算法1進(jìn)行約束轉(zhuǎn)換后的∨(W)中必定存在一條約束所以,f(m)≤wim.也就是說(shuō),線性約束(w,k)中的允許標(biāo)識(shí)包含于“邏輯或”的約束∨(W)中.故Aw,k?A∨(W).

如上所述,最后得到L∨(W)=Aw,k,則轉(zhuǎn)換后的“邏輯或”形式的線性約束W={(w1,k),…,(wn,k)}是最大允許的.

因此,根據(jù)定理1得知,例1中的“邏輯或”形式的線性約束W={(w1,k),(w2,k),(w3,k),(w4,k),(w5,k),(w6,k)},是最大允許的.

3 結(jié)束語(yǔ)

在離散事件系統(tǒng)中,系統(tǒng)的監(jiān)控問(wèn)題一直是研究的熱點(diǎn).而線性不等式約束轉(zhuǎn)換問(wèn)題仍是一大難題.針對(duì)不可控影響子網(wǎng)是α網(wǎng)的Petri網(wǎng),提出了將給定的原線性約束轉(zhuǎn)換為一組“邏輯或”形式的最大允許線性約束的算法.基于約束轉(zhuǎn)換的思想,含有不可控變遷的Petri網(wǎng)的監(jiān)控問(wèn)題可以簡(jiǎn)化為相當(dāng)于變遷全部可控的Petri網(wǎng)的監(jiān)控問(wèn)題,不可控變遷導(dǎo)致的復(fù)雜性由此降低,系統(tǒng)中的監(jiān)控問(wèn)題得到了更好的控制.但文中研究的Petri網(wǎng)的較小子類(lèi),將線性約束轉(zhuǎn)換問(wèn)題的研究推廣到更復(fù)雜的Petri網(wǎng)是今后研究的重點(diǎn).

[1]Yamalidou E,Moody J O,Antsaklis P J,et al.Feedback Control of Petri Nets Based on Place Invariants[J]. Automatica,1996,32(1):15-28.

[2]Moody J O,Antsaklis P J.Petri Net Supervisors for DES with Uncontrollable and Unobservable Transitions[J]IEEE Transactions on Automatic Control,2000,45(3):462-467.

[3]Moody J O,Antsaklis P J.Supervisory Control of Discrete Event Systems Using Petri Nets[M].New Jersey:Kluwer Academic Publishers,1998.

[4]Moody J O,Antsaklis P J,Lemmon M.Feedback Petri Net Control Design in the Presence of Uncontrollable Transition [C]//Proceedings of the IEEE 34th Conference on Decision and Control.Piscataway:IEEE,1995:905-906.

[5]Basile F,Carbone C,Chiacchio P.Feedback Control Logic for Backward Conflict Free Choice Nets[J].IEEE Transactions on Automatic Control,2007,52(3):387-400.

[6]Basile F,Chiacchio P,Giua A.Suboptimal Supervisory Control of Petri Nets in Presence of Uncontrollable Transitions via Monitor Places[J].Automatica,2006,42(6):995-1004.

[7]Luo J L,Wu W M,Su H Y,et al.Supervisor Synthesis for Enforcing a Class of Generalized Mutual Exclusion Constraints on Petri Nets[J].IEEE Transactions on Systems,Man,and Cybernetics-Part A Systems and Humans, 2009,39(6):1237-1246.

[8]Wang S,Wang C,Zhou M.Design of Optimal Monitor-based Supervisors for a Class of Petri Nets with Uncontrollable Transitions[J].IEEE Transactions on Systems,Man,and Cybernetics:Systems,2013,43(5):1248-1255.

[9]Luo J,Nonami K,Jin F.Maximally Permissive Supervisor Synthesis Based on a New Constraint Transformation Method[J].Automatica,2012,48(6):1097-1101.

[10]Luo J,Nonami K.Approach for Transforming on Linear Constraints on Petri Nets[J].IEEE Transactions on Automatic Control,2011,56(11):2751-2765.

[11]Wang S,Wang C,Yu Y.Comments on“Siphon-based Deadlock Prevention Policy for Flexible Manufacturing Systems”[J].IEEE Transactions on Systems,Man,and Cybernetics-Part A Systems and Humans,2011,41(2):338-340.

[12]Wang S,Wang C,Zhou M.Controllability Conditions of Resultant Siphons in a Class of Petri Nets[J]IEEE Transactions on Systems,Man,and Cybernetics-Part A Systems and Humans,2012,42(5):1206-1215.

[13]Basile F,Cordone R,Piroddi L.Compact Supervisors for General Constraint Enforcement in Petri Net Models with Uncontrollable Transitions[C]//European Control Conference.Piscataway:IEEE,2013:143-148.

[14]王安榮,李志武.基本信標(biāo)計(jì)算的一種快速算法[J].西安電子科技大學(xué)學(xué)報(bào),2008,35(4):632-638. Wang Anrong,Li Zhiwu.Effective Algorithm for Obtaining a Set of Elementary Siphons[J].Journal of Xidian University,2008,35(4):632-638.

(編輯:齊淑娟)

Optimal linear constraint transformation method forα-nets

ZHANG Li,ZHAO Liangxu,WANG Shouguang,WANG Chengying
(School of Information&Electronic Eng.,Zhejiang Gongshang Univ.,Hangzhou 310018,China)

For a class of Petri nets whose uncontrollable subnets areα-nets,this paper proposes a method to transform a given generalized mutual exclusion constraint into an optimal admissible one.Firstly,the uncontrollable subnets are obtained.Secondly,an algorithm for synthesizing the transformed sets of forbidden places is proposed.Lastly,according to the sets of forbidden places,the disjunction of admissible linear constraints which is maximally permissive is constructed.An example is provided to illustrate the efficiency of the proposed method.

Petri nets;discrete event systems;forbidden states;uncontrolled transitions

TP271+.8;TP301

A

1001-2400(2015)05-0183-05

2014-06-03< class="emphasis_bold">網(wǎng)絡(luò)出版時(shí)間:

時(shí)間:2014-12-23

浙江省杰出青年基金資助項(xiàng)目(LY15F030003,R14F020001);國(guó)家自然科學(xué)基金資助項(xiàng)目(61472361);浙江省科技計(jì)劃資助項(xiàng)目(2015C31064);浙江省新型網(wǎng)絡(luò)標(biāo)準(zhǔn)與應(yīng)用技術(shù)重點(diǎn)實(shí)驗(yàn)室資助項(xiàng)目(2013E10012)

張 麗(1989-),女,浙江工商大學(xué)碩士研究生,E-mail:wsg5000@hotmail.com.

趙良煦(1959-),男,副教授,E-mail:hzbz@zjgsu.edu.cn.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.030.html

10.3969/j.issn.1001-2400.2015.05.030