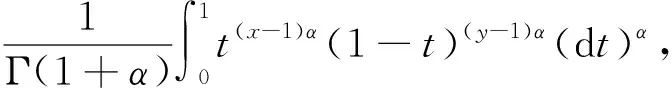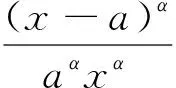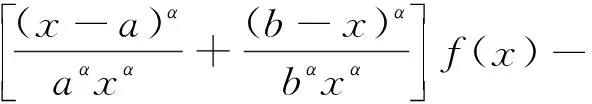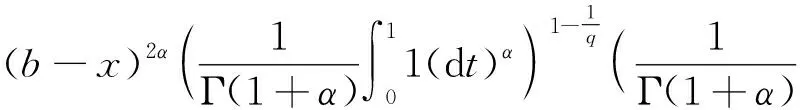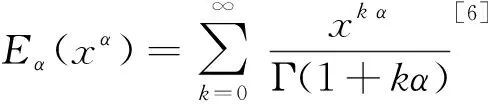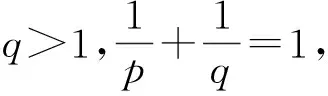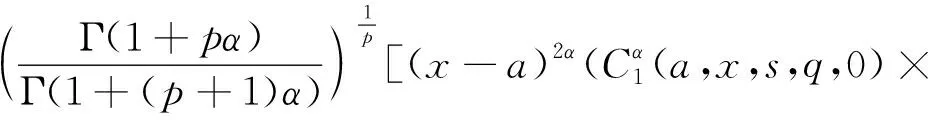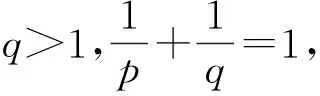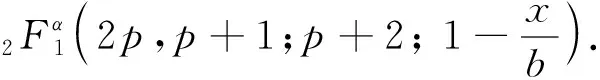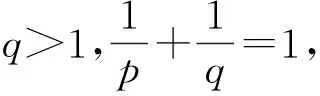Ostrowski type inequalities for generalized harmonically s-convex functions via local fractional integrals
SUN Wenbing
(School of Science, Shaoyang University, Shaoyang 422000, Hunan Province, China)
Abstract: Based on the theory of local fractional calculus on fractal sets, the author established an identity involving local fractional integrals. Using the identity, some generalized Ostrowski type inequalities for generalized harmonically s-convex functions were obtained.
Key Words: Ostrowski type inequality; generalized harmonically s-convex function; fractal set; local fractional integral
0 Introduction
Letf:I→R, whereI?Ris an interval, be a differentiable mapping inI° (the interior ofI) and leta,b∈I° witha (1) Definition1LetI?(0,∞) be a real interval. If (2) for allx,y∈Iandt∈[0,1] and for some fixeds∈(0,1], a functionf:I→Ris said to be harmonicallys-convex(concave). Local fractional calculus is one of the useful tools to handle the fractal and continuously nondifferentiable functions. In [6-7], YANG stated the theory of local fractional calculus on fractal space systematically. As a result, more and more researchers extended their studies to fractal space[8-13]. SUN[13]introduced the definition of generalized harmonicallys-convex function on fractal space. Definition2[13]A functionf:I?(0,∞)→Rα(0<α≤1) is said to be generalized harmonicallys-convex, if (3) for allx,y∈I,t∈[0,1] and for some fixeds∈(0,1]. If the inequality in (3) is reversed, thenfis said to be generalized harmonicallys-concave. Based on the theory of local fractional calculus and the definition of generalized harmonicallys-convex function, this paper established some generalized Ostrowski type inequalities for generalized harmonicallys-convex function on fractal space. LetRα(0<α≤1) be theα-type set of the real line numbers. Ifaα,bα,cα∈Rα, then the following operations satisfy(see[6-7]): (1)aα+bα∈Rα,aαbα∈Rα, (2)aα+bα=bα+aα=(a+b)α=(b+a)α, (3)aαbα=bαaα=(ab)α=(ba)α, (4)aα(bα+cα)=aαbα+aαcα, (5)aα+0α=0α+aα=aα,aα1α=1αaα=aα, (6) (a-b)α=aα-bα. The theory of the local fractional calculus onRαcan refer to references [6-7,12]. Here, we only make some explanations as follows: (1) Iff(x) is local fractional continuous on (a,b) , we denotef(x)∈Cα(a,b). (2) The local fractional derivative off(x) of orderαatx=x0is defined by Iff(x) is local fractional derivable on [a,b], we denotef∈Dα[a,b]. (3) The local fractional integral of functionf(x) of orderαis defined by Lemma1[6] (1) Suppose thatf(x)=g(α)(x)∈Cα[a,b], then (2) Suppose thatf(x),g(x)∈Dα[a,b], andf(α)(x),g(α)(x)∈Cα[a,b], then Lemma2[6] In order to simply the representation of results, we will introduce the following special functions on fractal sets. (1) The Beta function is given by x>0,y>0. (2) The hypergeometric function is given by c>b>0,|z|<1. Lemma5LetI?(0,∞) be an interval,f:I°?(0,∞)→Rα(I° is the interior ofI) such thatf∈Dα(I°) andf(α)∈Cα(a,b) fora,b∈I° witha (4) ProofLet (5) By the local fractional integration by parts, we have (6) Let (7) Similarly, we can get (8) Adding (6) and (8), we obtain This completes the proof. Theorem1LetI?(0,∞) be an interval,f:I°→Rα(I° is the interior ofI) such thatf∈Dα(I°) andf(α)∈Cα[a,b] fora,b∈I° witha (9) where ProofTaking modulus in equality (4), by the generalized H?lder’s inequality (lemma 3) and the generalized harmonicallys-convexity of |f(α)|qon [a,b], we have And now, Joe, I am seventy-nine years old. I have my health, I feel good and I am in love with my wife just as I was when we first met. This is the best time of my life. (10) By lemma 4, it is easily check that (11) Further calculation, we have (12) (13) Changing the variable with 1-t=r, we have (14) Similarly, (15) Thus, using (11)~(15) in (10), we can obtain the inequality of (9). This completes the proof. Theorem2LetI?(0,∞) be an interval,f:I°→Rα(I° is the interior ofI) such thatf∈Dα(I°) andf(α)∈Cα[a,b] fora,b∈I° witha (16) ProofTaking modulus in equality (4), by the generalized H?lder’s inequality(lemma 3) and the generalized harmonicallys-convexity of |f(α)|qon [a,b], we have (17) By calculating, it is easily checked that (18) and (19) Further calculation, we have (20) (21) (22) and (23) Thus, using (18)~(23) in (17), we can obtain the inequality of (16). This completes the proof. (24) ProofTaking modulus in equality (4), by the generalized H?lder’s inequality(lemma 3) and the generalized harmonicallys-convexity of |f(α)|qon [a,b], we have (25) By calculating, it is easy to check that (26) Further calculation, we have (27) (28) (29) and, (30) Thus, using (26)~(30) in (25), we can obtain the inequality of (24). This completes the proof. (31) ProofTaking modulus in equality (4), by the generalized H?lder’s inequality(lemma 3) and the generalized harmonicallys-convexity of |f(α)|qon [a,b], we have (32) By calculating, it is easily checked that (33) Further calculation, we have (34) and (35) Thus, using (33)~(35) in (32), we can obtain the inequality of (31). This completes the proof. (36) ProofTaking modulus in equality (4), by the generalized H?lder’s inequality(lemma 3) and the generalized harmonicallys-convexity of |f(α)|qon [a,b], we have (37) By calculating, it is easily checked that (38) and (39) Applying the change of the variableta+(1-t)x=v, we have (40) (41) Similarly, using the change of the variabletb+(1-t)x=w, we have (42) Thus, using (38)~(42) in (37), we can obtain the inequality of (36). This completes the proof.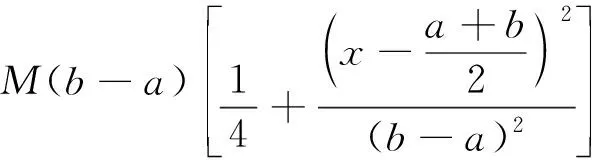

1 Preliminaries
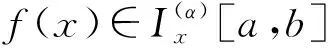
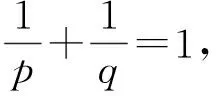
2 Main results