蘇倩倩

(鄭州成功財經(jīng)學院通識教育中心,河南鄭州 451200)

1 引言

Leslie-Gower作為一個重要的生態(tài)系統(tǒng)模型,已經(jīng)引起了許多學者的關注,并且得到了很多好的結果(見文獻[1–12]及所引文獻).但是,對于生命短,世代不重疊的種群或者雖然生命長,世代重疊的種群在其數(shù)量少的時候,用差分方程(離散的動力模型)來表示更為合理(見文獻[13]).鑒于此,本文將研究如下離散的Leslie-Gower模型

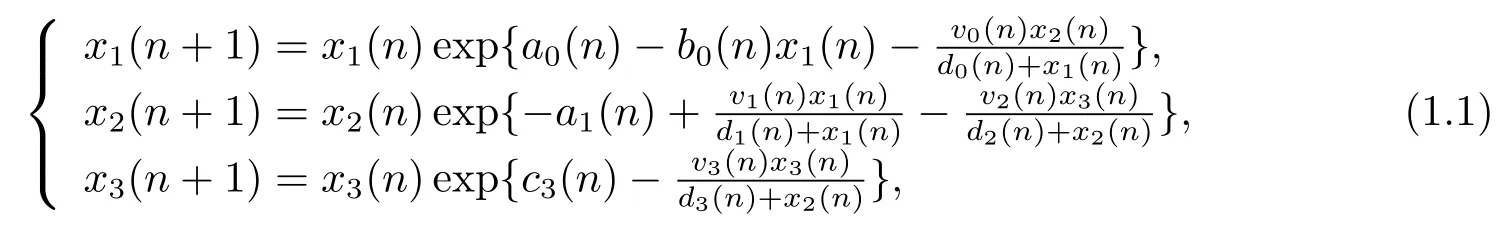
其中xi(n)(i=1,2,3)為種群i在n時刻的密度,a0,b0,v0,d0,a1,v1,d1,v2,d2,c3,v3和d3均為連續(xù)的有正的上下界的序列,且xi(0)≥0(i=1,2,3).

文[2]對離散兩種群Leslie-Gower模型的周期解和全局吸引性進行了研究,而文[3]首次提出了一類連續(xù)的三種群Leslie-Gower模型.一個自然而然的問題是:離散三維Leslie-Gower模型的動力學行為又將怎樣呢？據(jù)筆者所知,至今尚未有學者研究離散三維Leslie-Gower模型.本文參照文[14]的分析手法來研究系統(tǒng)(1.1)的動力學行為.更多有關Leslie-Gower模型的背景可以參考文獻[3].這里對任意的序列{a(n)},記au=.

2 引理

引理2.1[15]假設序列{x(k)}滿足x(k)>0,a(k)和b(k)為有正的上下界的非負序列,若x(k+1)≤x(k)exp{a(k)?b(k)x(k)},k∈N,則

引理2.2[16]假設序列{x(k)}滿足x(k)>0,a(k)和b(k)為有正的上下界的非負序列,若x(k+1)≥x(k)exp{a(k)?b(k)x(k)},k≥N0,x(N0)>0,其中N0∈N,且,則

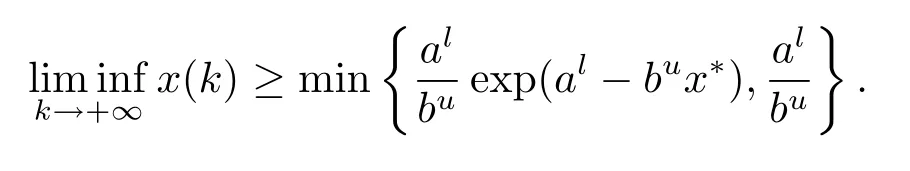
3 持久性與全局吸引性

定理3.1若

成立,則種群x1與x3持久,而種群x2絕滅.

證設x(n)=(x1(n),x2(n),x3(n))T為系統(tǒng)(1.1)的任意正解.由系統(tǒng)(1.1)的第一個方程得

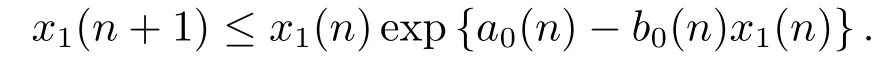
由引理2.1,得到

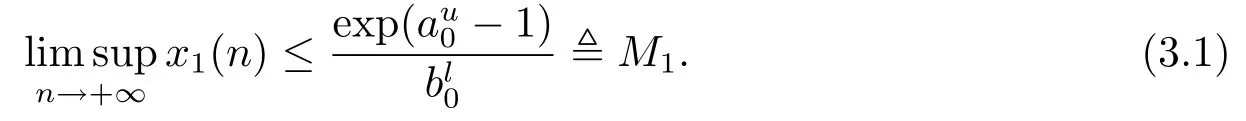
由系統(tǒng)(1.1)的第二個方程可得

由條件(H1)知

所以對于足夠小的ε>0,存在N1>0,N1∈N,對任意n>N1,都有

由系統(tǒng)(1.1)的第三個方程得

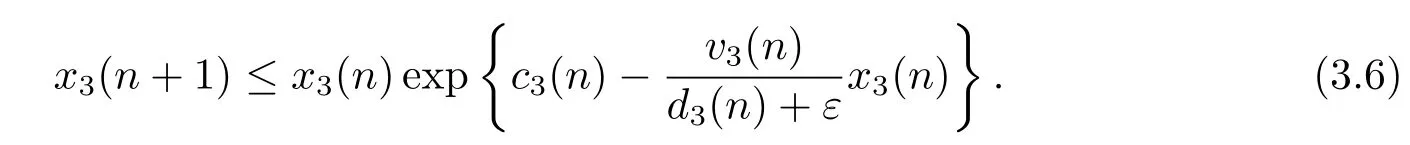
由引理2.1知

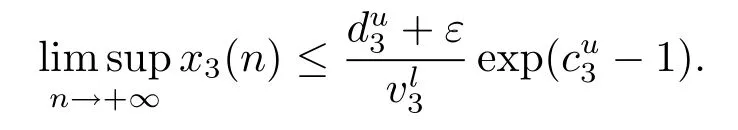
令ε→0得

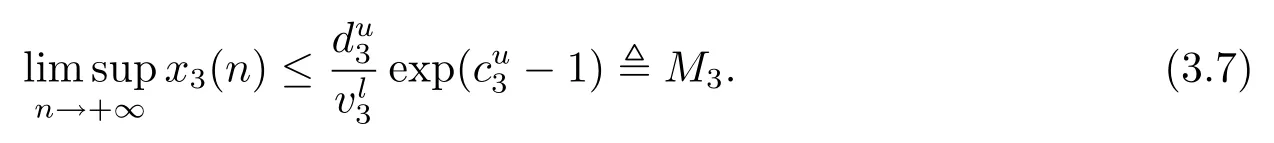
則對于上述ε>0,存在N2>N1,N2∈N,對任意n>N2,都有

所以

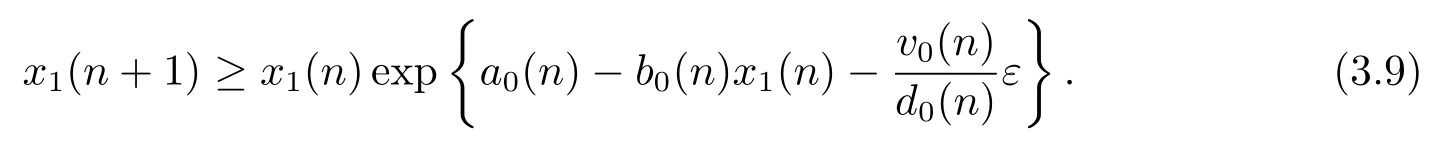
因為ε足夠小,所以仍為正序列.則由引理2.2知

令ε→0得

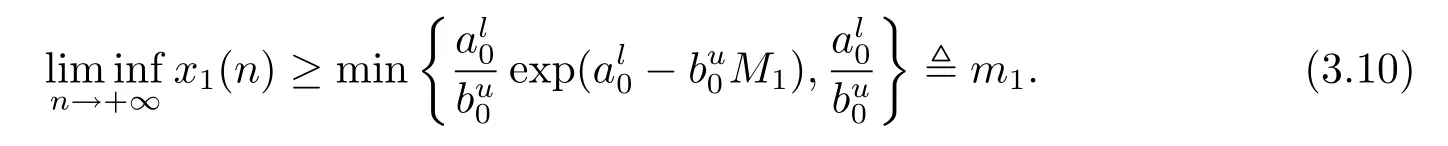
由系統(tǒng)(1.1)的第三個方程得

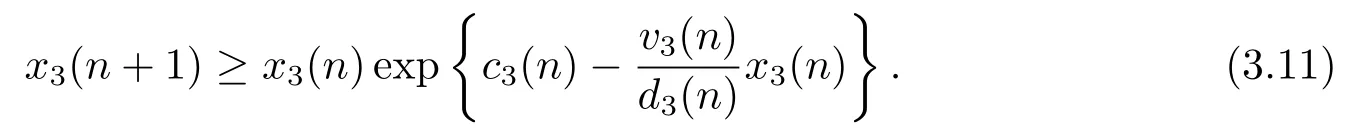
由引理2.2知

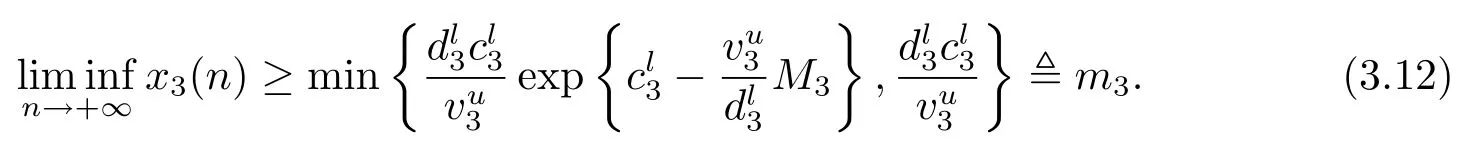
下證M1>m1.

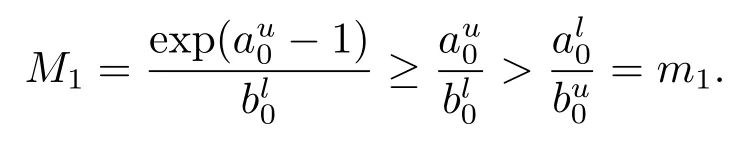
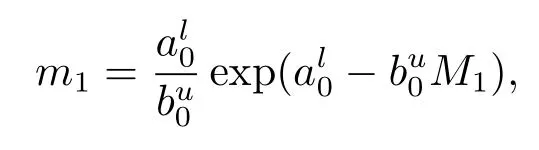
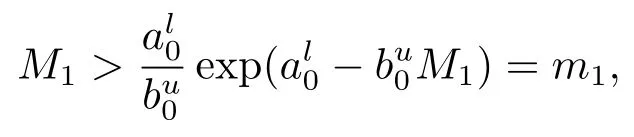
綜上所述M1>m1,同理可以證明M3>m3.定理3.1證畢.

定理3.2假設(H1)成立,且

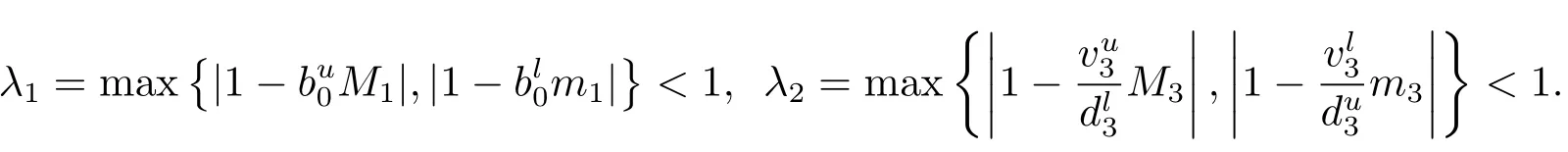
則系統(tǒng)(1.1)是全局吸引的.

證設為系統(tǒng)(1.1)的任意兩個正解.因為,由定理3.1知,則.所以對于上述的ε>0,存在N3>N2,N3∈N,對于任意的n>N3,都有

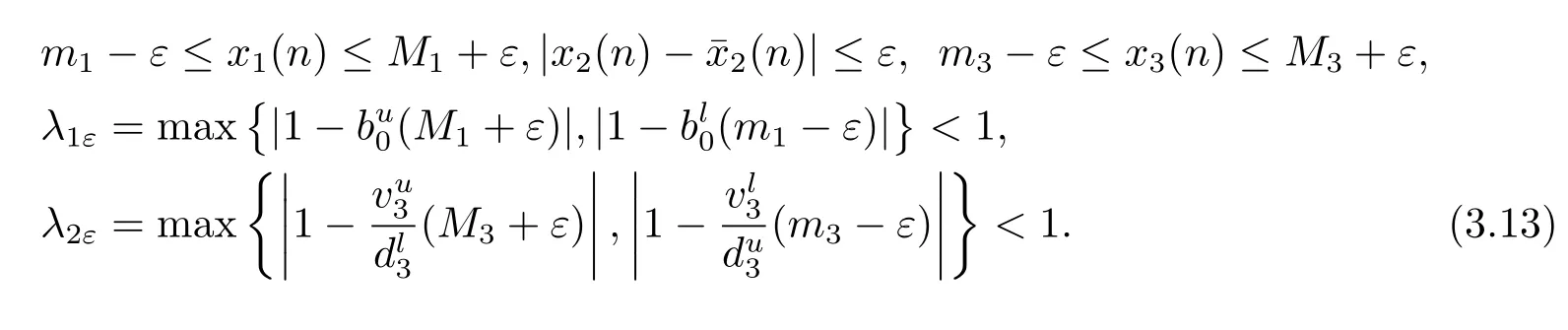
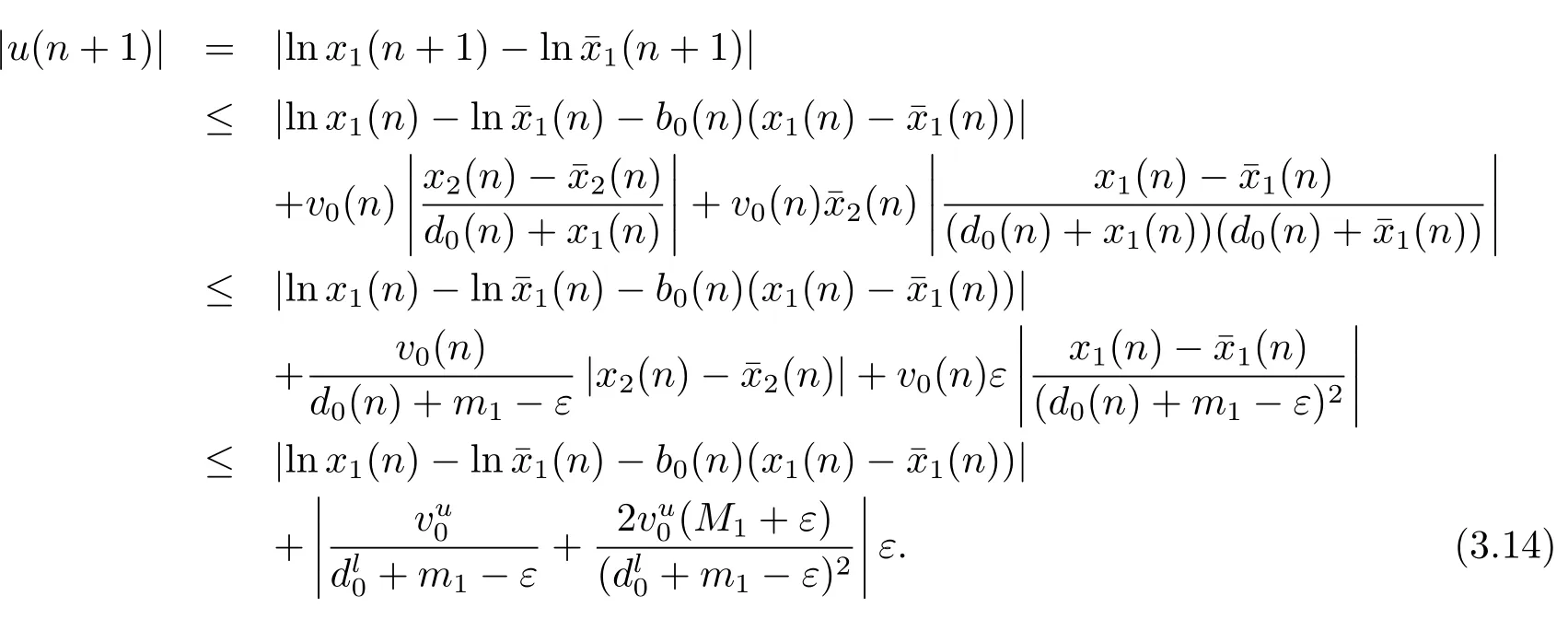
當n>N3時,有m1?ε≤ξ1(n)≤M1+ε.則由(3.13),(3.14)式知

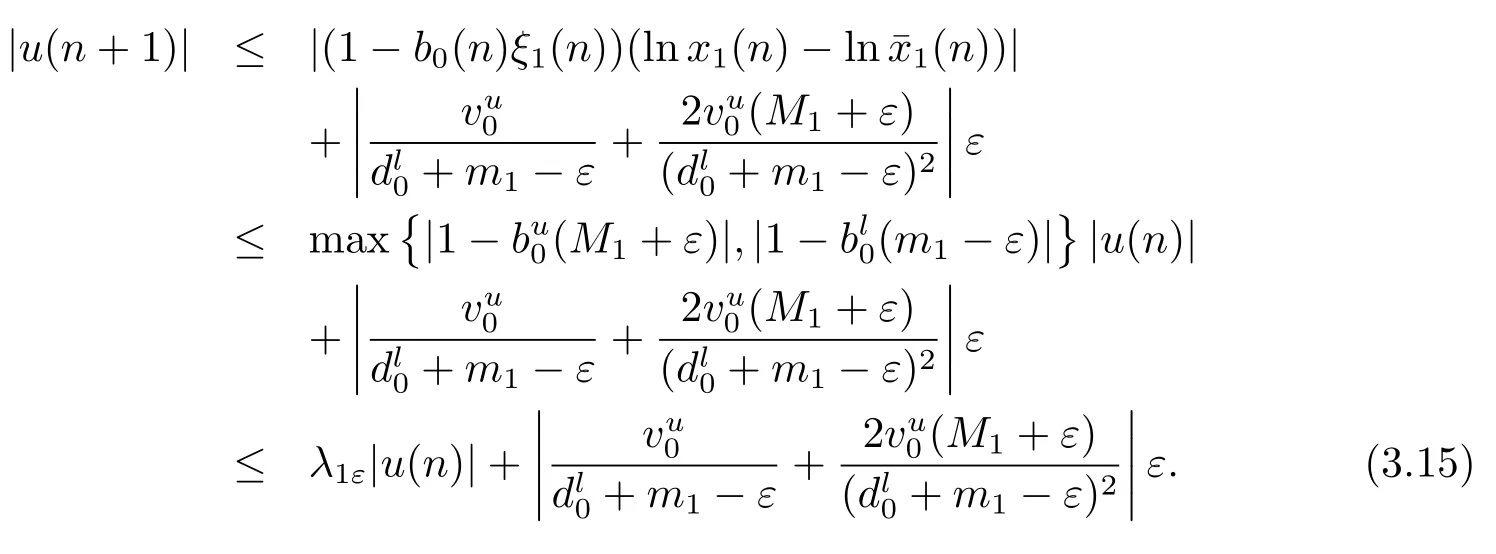
令ε→0 得|u(n+1)|≤λ1|u(n)|.因此,所以

當n>N3時,有

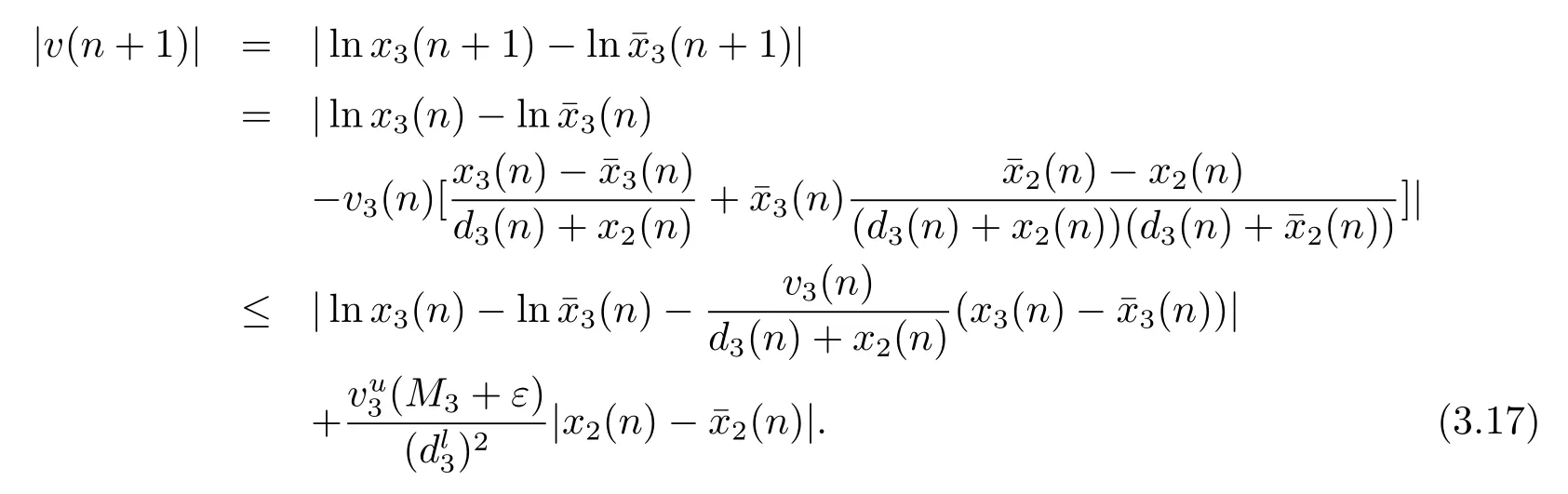
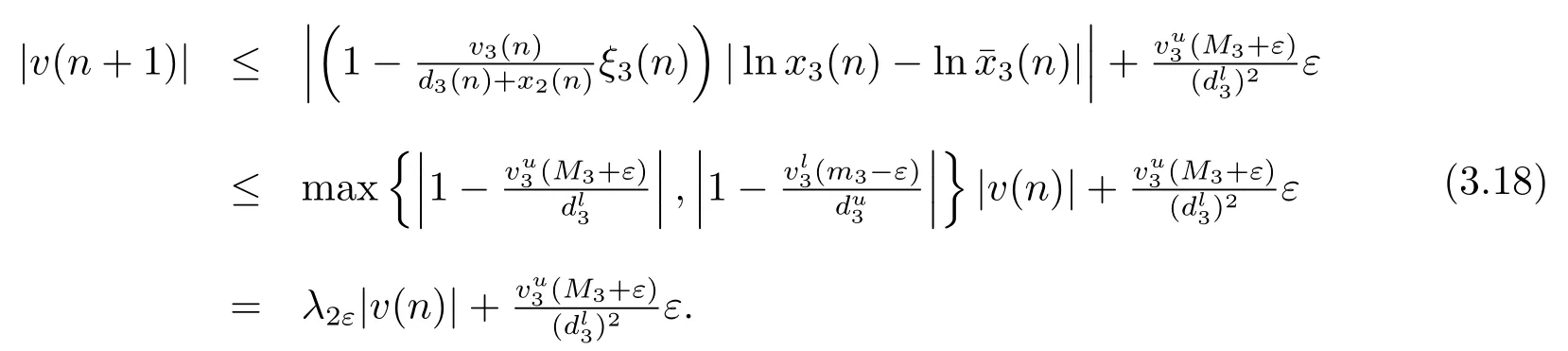
令ε→0 得|v(n+1)|≤λ2|v(n)|.因此,所以

定理3.2證畢.

4 數(shù)值模擬

例4.1考慮下面的系統(tǒng)

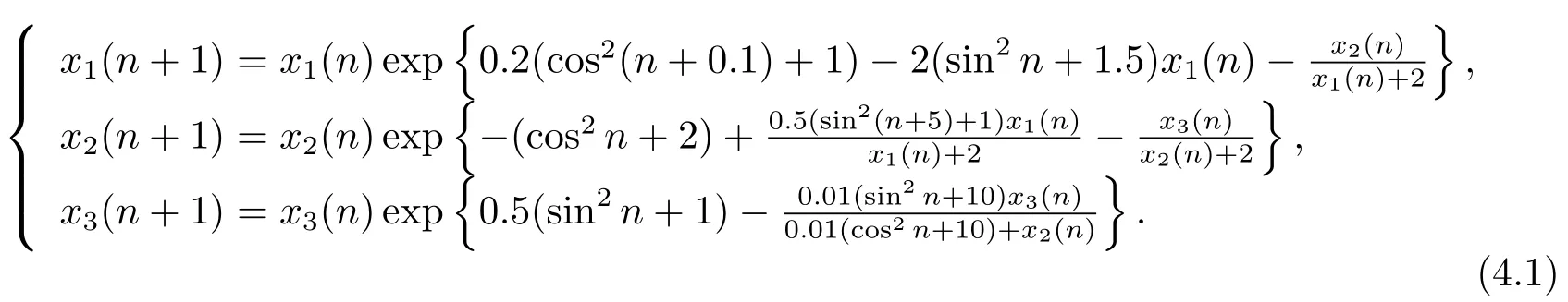
對應于系統(tǒng)(1.1),計算可知

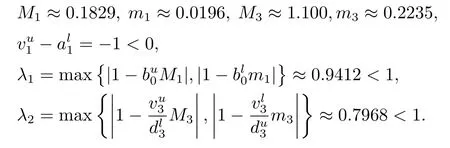
滿足定理3.1和定理3.2的條件,下面給出系統(tǒng)(4.1)的模擬圖像.

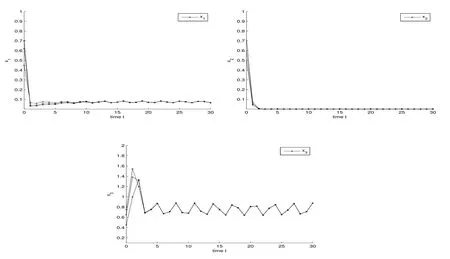
圖1:具有初始條件(x1(n),x2(n),x3(n))T=(0.62,0.60,0.65)T,(0.7,0.72,0.45)T,(0.45,0.5,0.75)T系統(tǒng)(4.1)的動力學行為

5 結論

本文研究了一類離散Leslie-Gower三維食物鏈模型,首先運用差分不等式的有關結論得到:若(H1)成立,則種群x1,x3持久x2絕滅,即當中級捕食者x2的死亡率大于食餌x1的人均減少率的最大值時,高級捕食者x3和食餌x1持久生存,而中級捕食者x2將走向絕滅.其次,通過采用文[14]的手法,構造適當?shù)牟罘諰yapunov函數(shù),得到了該系統(tǒng)全局吸引的充分性條件.文[2]研究了離散兩種群Leslie-Gower模型的周期解和全局吸引性,文[3]首次提出并研究了一類連續(xù)的三種群Leslie-Gower模型,證明了該系統(tǒng)的有界性,吸引集的存在性,以及表示高級或中級捕食者滅絕的均衡的局部或全局穩(wěn)定性.但文[17]指出,文[3]中關于有界解和不變吸引集的結論是錯誤的.所以對于連續(xù)模型的動力學行為還有待進一步研究.本文是在文[3,17]的基礎上研究了離散三種群Leslie-Gower模型,是對文[2]的補充和完善.最后,數(shù)值模擬說明結論是可行的.