云南省玉溪第一中學(xué)

1 “糖水不等式”的科學(xué)背景

人教普通高中課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書A版(2007年1月第2版)數(shù)學(xué)選修4-5“不等式選講”第21頁(yè)有這樣一道例題:

如果用akg 白糖制出bkg 糖溶液,則糖的質(zhì)量分?jǐn)?shù)為

可以把上述事實(shí)抽象成如下不等式問題:

糖水不等式已知b>a>0,m>0,則

用比較法很容易證明此不等式,此處從略.為了方便表述,我們把上述不等式稱之為“糖水不等式”(此不等式可以理解為糖水加糖變甜了).

2 深層理解“糖水不等式”

3 “糖水不等式”的本質(zhì)

4 “糖水不等式”的推論

推論1[3]若b>a>0,m>0,則

推論2[5]若b1> a1>0,b2> a2>0,則此推論可以理解為,把兩杯濃度不同的糖水混合在一起,所得糖水一定是比濃的糖水淡一些,比淡的糖水甜一些.

5 “糖水不等式”的應(yīng)用

5.1 “糖水不等式”的正向應(yīng)用

例1[1](2008年全國(guó)高中數(shù)學(xué)聯(lián)賽山東省預(yù)賽題)

若x >0,y >0,z >0,且xyz=1,求證:1<

證明依題意,可設(shè)

則

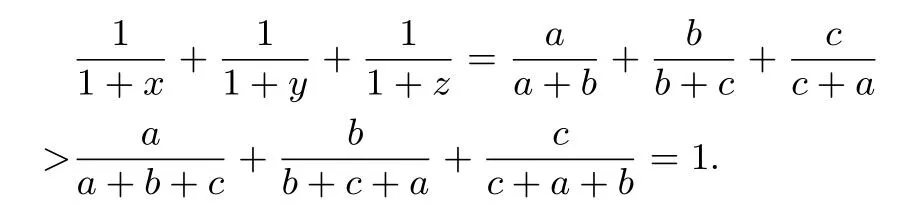
綜上,原不等式得證.

例2[7](2009年高考山東卷)等比數(shù)列{an}的前n項(xiàng)和為Sn.已知?n ∈N?,點(diǎn)(n,Sn)均在函數(shù)y=bx+r(b>0,且b ?=1,b,r均為常數(shù))的圖象上.

(1)求r的值;

(2)當(dāng)b=2時(shí),記bn=2(log2an+1)(n ∈N?),證明:?n ∈N?,不等式恒成立.

解(1)略.(2)由(1)知,an=(b-1)bn-1.當(dāng)b=2時(shí),易知bn=2n,故要證明的不等式為

5.2 “糖水不等式”的逆向應(yīng)用

例3[6](2015年高考安徽卷)設(shè)n ∈N?,xn是曲線y=x2n+2+1 在點(diǎn)(1,2)處的切線與x軸交點(diǎn)的橫坐標(biāo).

(1)求數(shù)列{xn}的通項(xiàng)公式;

解 (1)(求解過程略).(2)由已知和(1),得

當(dāng)n=1時(shí),不等式成立.當(dāng)n ≥2時(shí),由“糖水不等式”,得所以綜上所述,對(duì)任意的n ∈N?,均有

例4[6](2013年北京大學(xué)自主招生測(cè)試題)正數(shù)a,b,c滿足a

證明因?yàn)閍

因?yàn)閍,b,c均為正數(shù),且2bc > bc,由“糖水不等式”,得而由已知正數(shù)a,b,c滿足a < b+c,可得b+c-a >0,故從而

例5[4](1998年全國(guó)高考題)已知數(shù)列{bn}是等差數(shù)列,b1=1,b1+b2+···+b10=145.

(1)求數(shù)列{bn}的通項(xiàng)bn;

(2)設(shè)數(shù)列{an}的通項(xiàng)an=a >0,且a ?= 1),記Sn是數(shù)列{an}的前n項(xiàng)和,試比較Sn與的大小,并證明你的結(jié)論.

解(1)bn=3n-2 (過程從略).

(2)Sn=loga

因此,要比較Sn與的大小,可先比較與的大小,即比較與3n+1的大小,即比較與3n+1的大小.

由此證得:當(dāng)a >1時(shí),當(dāng)0< a <1時(shí),