Da-lin Tan, Ji-fu Zhou, Xu Wang

1. Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

2. School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Abstract: The fission of solitary waves propagating over variable topography is investigated. In previous theories, to predict the number and the amplitudes of disintegrated solitons in the wave packet generated from a solitary wave, the parameters of the water environment and the incident solitary wave are required. However, it is difficult to measure these parameters in the ocean because of their temporal and spatial variations. In this paper, a fission law, in the form of the expressions of the number and the amplitudes of the disintegrated solitons, is derived from the partial information available on the wave packet. Theoretical analysis shows that the law is suitable for describing the fission of both surface and internal solitary waves and is also applicable to the cases of wave damping and wave breaking. Comparisons between the model output and the results from laboratory experiments, numerical simulations and field observations available in the literature demonstrate that the fission law can efficiently estimate the number and the amplitudes of solitons in the wave packet generated by a solitary wave.

Key words: Fission law, solitary wave packet, wave breaking

Introduction

The solitary wave packets are ubiquitous in the ocean and play a significant role in the biological processes[1-2], the sediment transport[3-4]and the offshore engineering[5-10]. In examining the satellite images of 116 internal wave packets from 1995 to 2001 in the South China Sea (SCS), Zhao et al.[11]found that all internal wave packets on the continental shelf of the SCS are composed of rank-ordered internal solitary waves. Near the continental shelf break in the SCS, Ramp et al.[12]observed that highly nonlinear internal soliton packets were responsible for the most energetic motions recorded by moored and shipboard observations. More recently, seven packets of internal solitary waves were observed near the Dongsha Plateau from the synchronized satellite and hydrographic observations[13]. A widely accepted view is that these wave packets are generated from the fission of solitary waves as they encounter sharply varying topographies (e.g., the shelf break, the submerged plateau or the seamount). The studies of the propagation of solitary waves over simplified topography could provide useful insight into the wave evolution. To this end, the present paper investigates the fission and the disintegration of solitary waves propagating over a step.

When the solitary waves evolve over a variable topography, the wave breaking is often observed in both laboratory experiments[14-16]and field observations[17]. The conventional depth integrated models are unsuitable for studying breaking waves[18],so the development of alternative models is desirable.Liu and Cheng[18]employed a numerical model that couples the Reynolds averaged Navier-Stokes equations and the k-ε turbulence equations to investigate the evolution of a solitary wave breaking over a step. A similar model using the Volume-Averaged Reynolds Averaged Navier-Stokes equations was developed to analyze the attenuation of breaking solitary waves over a porous step[19].

When the parameters of the water environment(e.g., the density, the salinity and the temperature) and the initial conditions of the waves (e.g., the waveform and the amplitude) are well constrained, the model outputs are in good agreement with experimental results. However, the parameters of the water environment vary in time and space and the accurate estimates of the initial conditions are rarely possible.Therefore, these models are unsuitable for the study of the fission and the disintegration of solitary waves in practical applications.

In the present paper, a model is presented to predict the fission and the disintegration of solitary waves propagating over a step. The number and the amplitudes of disintegrated solitons in a solitary wave packet are derived from the amplitudes of the first two solitons, without the need for accurate estimates of environmental parameters and initial conditions. The model is validated by laboratory experimental results,field observations and numerical simulations. It is proved to be able to predict the number and amplitudes of disintegrated solitons in the case of wave breaking.

1. Model description

The evolution of solitary waves over a variable topography was extensively studied using nonlinear equations. The predictions of many of the models are in good agreement with experimental and in situ data.To investigate the fission of solitary waves over a step,the variable-coefficient KdV equation is used[20-21]

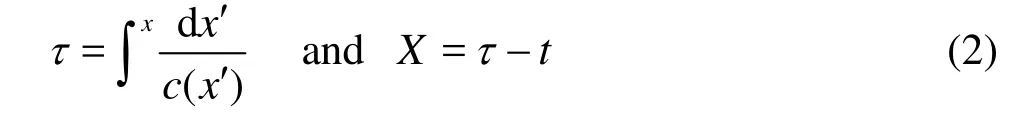
Equation (1) can be reduced to Eq. (3), with the same leading order of approximation

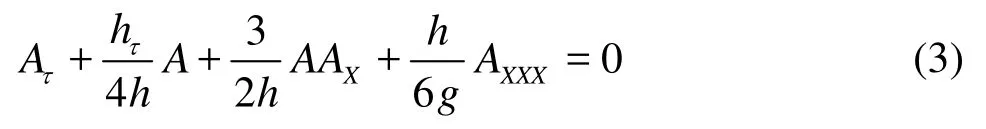
Defining B as

Equation (3) can be written as

where B is the wave amplitude in the transformed space (τ,X), and the coefficients υ and δ are functions of τ. For a constant wave depth, the coefficients υ and δ are constants and the solution of Eq. (5) is given by VBυ is the wave speed in the transformed space. Given the amplitude of a solitary wave, the waveform can be determined.

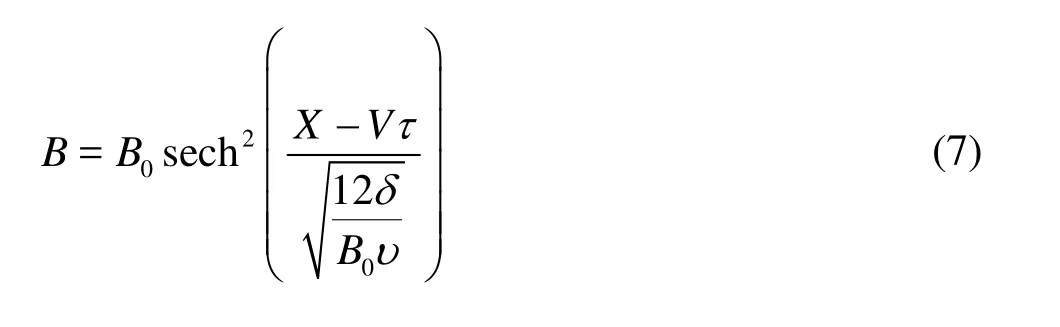
For a step characterized by an upstream water depth h1and a downstream depth2<1

where B0is the wave amplitude, =0/3 hh, the corresponding coefficients are1υ,1δ and2υ,2δ. A solitary wave with the amplitude B0propagating over this step would split into a series of solitons. The number and the amplitudes of these disintegrated solitons can be expressed as[22]

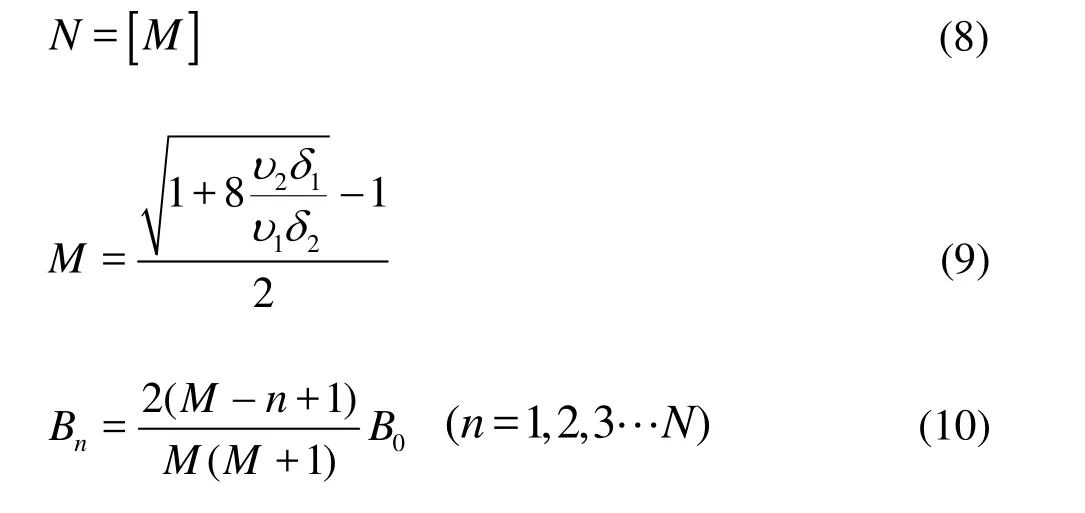
where N is the soliton number, […] denotes the rounding up to an integer and Bnis the amplitude of thethn soliton. Given h1, h2and B0, this theory is able to predict the number and the amplitudes of the disintegrated solitons. However, it is difficult to measure the initial position of a wave packet, let alone the amplitude of the initial solitary wave. It would be more practical to predict the information of the entire wave packet using some partial information available.In the transformed space, substituting the amplitudes of the two leading solitons B1and B2into Eq. (10),Eqs. (9) and (10) can be written as:

From Eqs. (8), (13) and (15), the number and the amplitudes of all solitons in a soliton series can be determined through the observed amplitudes of the first two solitons.

2. Model validation for the case of nonbreaking solitary waves

2.1 Comparison of model output with experimental results

Seabra-Santos et al.[14]conducted experiments to investigate the fission of solitary waves over a shelf,18.0 m long and 0.1 m high. In Fig. 1, the ratio between A0, the amplitude of the incident wave and

A the amplitude of the disintegrated solitary wave, is plotted against the ratio between A0and H, the water depth in front of the step in cases 1# to 31# as obtained by Seabra-Santos et al.. The 31 cases are divided into five groups according to the water depth and are presented in Figs. 1(a)-1(e). In each case, the amplitude of the third soliton as predicted by the KdV model is also plotted. The amplitudes of the incident waves were measured at the place 3.0 m in front of the step in the experiments. To avoid the appreciable damping on the step, the amplitudes of the disintegrated solitons were measured as close to the step as possible. Experimental results show that the amplitudes and the numbers of the disintegrated solitons increase with the decrease of the water depth.Figures 1(a)-1(c) show that only two disintegrated solitons are observed in these experiments, namely,the amplitude of the third soliton is zero. From Eq.(15), the amplitudes of the third solitons in the same experiments are also estimated to be near zero. In the calculations, only the input of the amplitudes of the two leading solitons is required; the input of the water depth, the wave amplitude and the step height is not necessary. Similarly, Figures 1(d), 1(e) show that the numbers of the disintegrated solitons observed in these experiments match those predicted by the model in very good agreement.

2.2 Comparison of model output with numerical results

In the experiments of Seabra-Santos et al., the amplitudes of the disintegrated solitons were measured as close to the step as possible to avoid the significant damping on the shelf. In this section, we assess the performance of the model under the conditions where the damping is present. Lara et al.[19]conducted numerical simulations based on the volume-averaged Reynolds averaged Navier-Stokes equations to investigate the effect of the wave damping on the soliton disintegration and evolution along the step for both breaking and non-breaking solitary waves. The amplitudes of the disintegrated solitons calculated from the Navier-Stokes model are plotted in Fig. 2 together with the amplitudes of the third soliton calculated from the KdV model. The disintegrated solitons are clearly visible between x/h1=60 and x/h1=85. A reasonable overall agreement between the two models is observed. Small deviations of the model results can be attributed to the differences between the Navier-Stokes model and the KdV model based on the assumptions of weak nonlinearity.

2.3 Comparison of model output with in situ observations

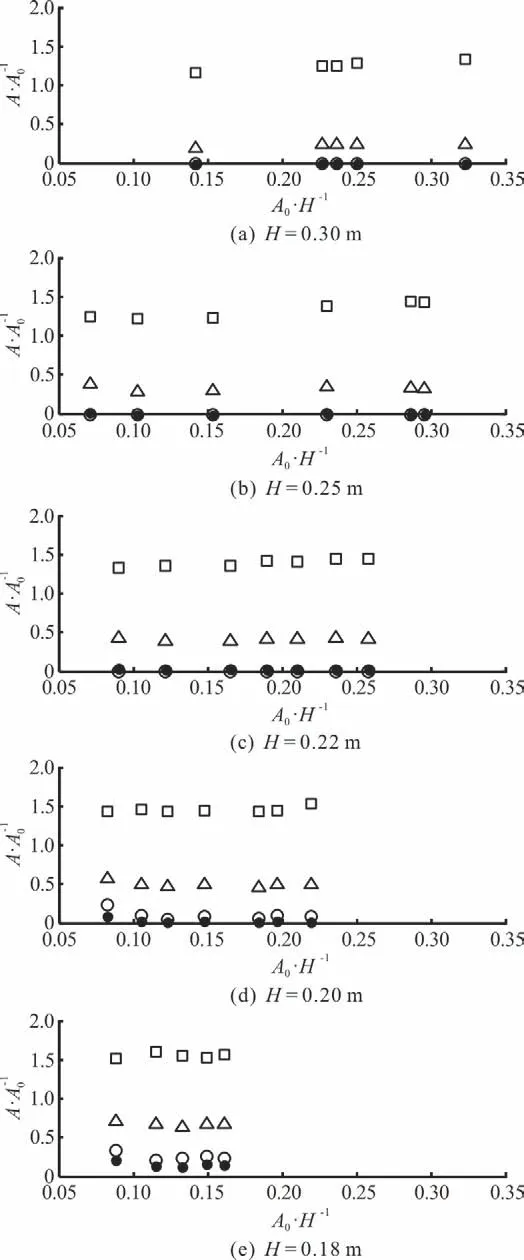
Fig. 1 Amplitudes of first (□), second (△), and third (○) disintegrated solitons from experiments of Seabra-Santos et al.[14] compared with the amplitudes of the third soliton as predicted by the present model (●). H is the water depth in front of the step, A0 is the amplitude of the incident wave and A is the amplitude of the disintegrated solitary wave

The internal solitary waves are frequently observed in the form of wave packets on the continental shelf of the SCS. These wave packets are generated in response to the sharply varying topography of the seabed. The amplitudes of solitons contained in an internal wave packet are much larger than the amplitude of a single internal solitary wave in the deep ocean because of the shoaling sand the shallow water environment. Consecutive solitons induce stronger shear current and, hence, pose greater threat to offshore structures.

The variable coefficient KdV equation used to model the internal solitary waves propagating over variable topography can be written as[23]

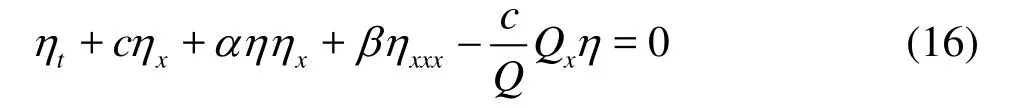
where η is the amplitude of the internal solitary waves, c is the linear long wave phase speed and α, β, Q are the coefficients of the nonlinear term,the dispersive term and the amplification factor of the linear long internal wave, respectively. These coefficients can be expressed as:

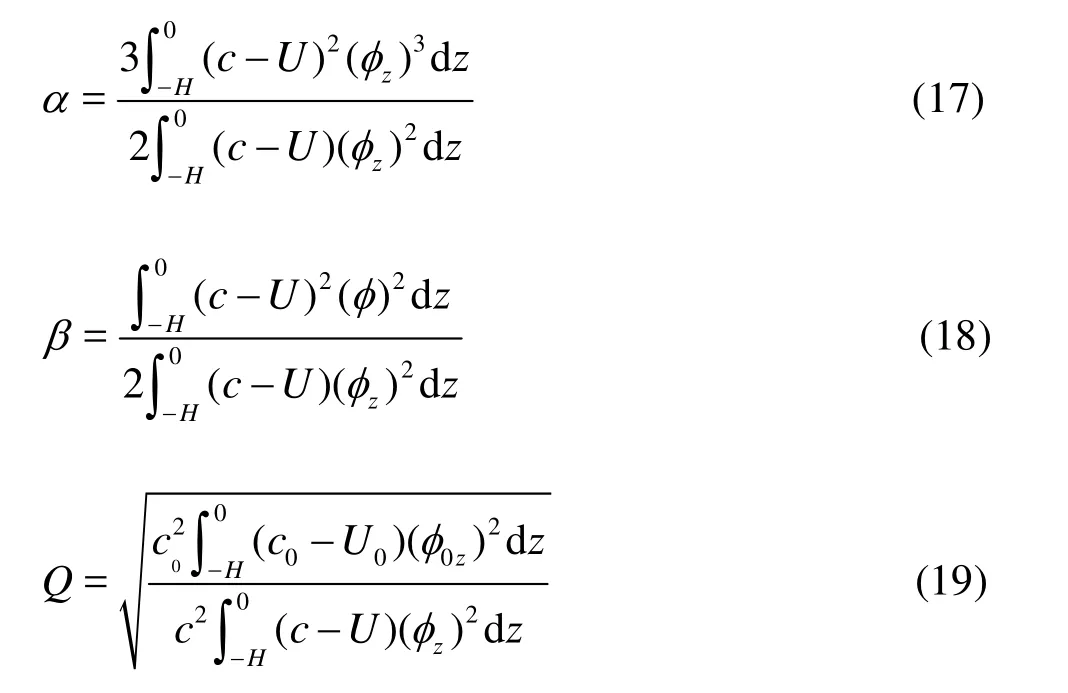
where U is the background current, the terms with subscript 0 are evaluated at the initial position and the phase speed c and the modal function φ are determined from the Taylor-Goldstein equation[24]

The form of Eq. (22) is exactly the same as that of Eq.(5). Therefore, the information of the internal solitary waves can be obtained following the steps outlined in Section 2.

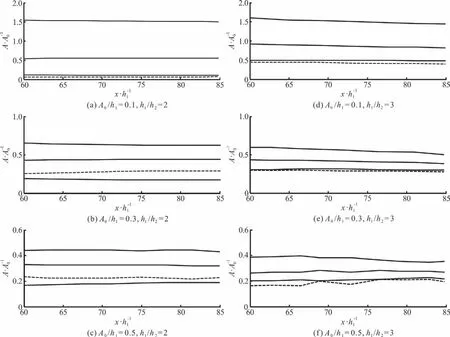
Fig. 2 Amplitudes of first, second and third disintegrated solitons from the Navier-Stokes model of Lara et al.[19] (solid lines) compared with amplitude of the third soliton as predicted by the KdV model (dashed line). h1 and h2 are the water depths before and after the step, A0 is the amplitude of the incident wave, A is the amplitude of the disintegrated solitary wave and x is the distance from the step

The coefficients in Eq. (5) only depend on the topography. However, the coefficients in Eq. (22) are more complicated to calculate because firstly, they depend on both the topography and the stratification and secondly, the density stratification in the ocean varies with space and time. The traditional prediction method that uses Eqs. (8), (9) and (10) has limitations of the application to the real oceanic environment.

Equation (22) was used to simulate the fission of internal solitary waves over a seamount with a water depth of 400 m to 100 m as observed from a space shuttle over the SCS[25]. Photographs taken from the space shuttle show that as two internal solitary waves propagate from deep to shallow waters they are disintegrated into two soliton packets. Table 1 shows a comparison of the amplitudes of the solitons in the wave packets obtained from the photographs and those from the KdV model. A good agreement is observed between the model output and the space shuttle observations of the amplitudes of the third soliton in both wave packets, but with a discrepancy for the numbers of solitons in each wave packet.Several factors could be the cause of this discrepancy.The fourth and fifth solitons may have been undetectable from the space because they are much smaller in amplitude than the first soliton. Because the wave packets were generated from consecutive solitary waves, the packets overlapped with each other.This could cause the fourth and fifth solitons of the first wave packet to be obscured by the front of the second packet for the accurate measurement of the first solitons of the second packet. In the model, the number and the amplitudes of all solitons in a soliton series are determined through the observed amplitudes of the first two solitons. Therefore, errors in the observed amplitudes of the first two solitons in the second packet could lead to further errors in the model’s prediction of subsequent solitons.

3. Model validation for the case of breaking solitary waves

Large-amplitude solitary waves are often very energetic, and their breaking can usually be observed during the shoaling process. Breaking mechanisms include the bottom boundary layer instabilities, theshear instabilities in the interior of the water column and the wave overturning as they shoal[17]. Solitary waves with larger amplitudes are more likely to break due to stronger interactions with the bottom topography and the greater instability in both the bottom boundary layer and the interior of the water column. In the rank-ordered wave packets, the leading solitons are more likely to break than the subsequent solitons because of the relatively large amplitudes of the leading solitons.

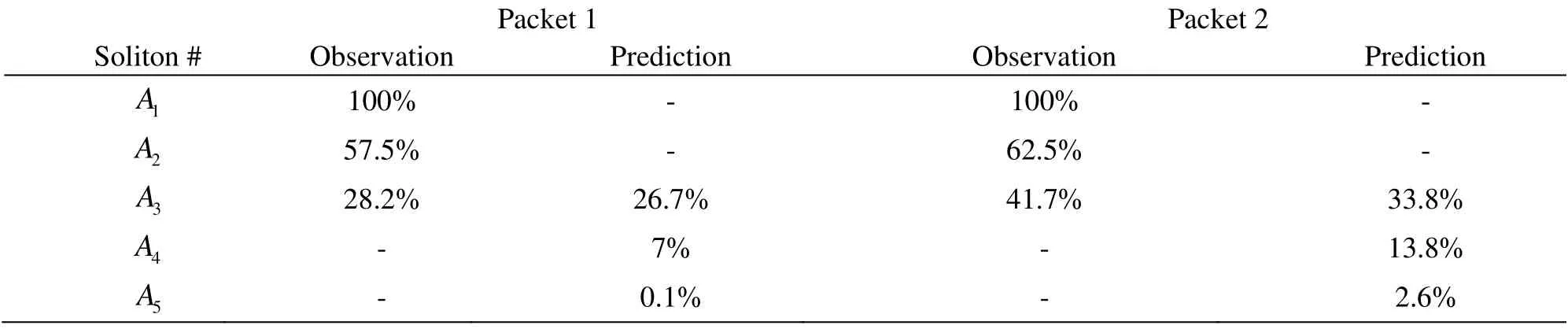
Table 1 Comparison of amplitudes of solitons obtained from space shuttle observations and model

Similar to the disintegration process, the wave breaking is often triggered by a variable topography.Hence, both the fission and the wave breaking could happen for an internal solitary wave propagating across a sharply varying topography. Seabra-Santos et al.[14]and Losada et al.[15]conducted experimental studies of breaking solitary waves over a step and observed that the fission continues even if the wave breaking occurs after the start of the fission. In this section, we examine the fission process that takes place behind a breaking solitary wave.

After propagating over a step, an incident solitary wave evolves into N solitons with a decreasing order of amplitude. When the amplitudes of the solitons are very large, they may break. In this case,the amplitudes of the subsequent unbroken solitons can still be predicted by the theory stated in Section 2.Supposing that m leading solitons break because of their large amplitudes, then the number of solitons in the wave packet is N-m. Using Eq. (10), the amplitudes of the two leading solitons in the packets Bm+1, Bm+2can be written as:

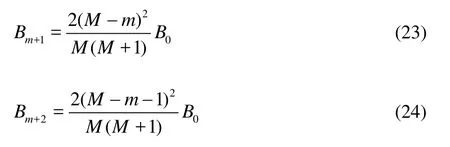
Then, in the transformed space, the number and the amplitudes of the solitons in the wave packet can be expressed as

For m=0, Eqs. (25), (27) are exactly the same as Eqs. (13), (15), respectively, namely, when the fission occurs before the wave breaking, a wave packet containing the disintegrated solitons will subsequently emerge behind the breaking solitons, and the fission law obtained in Section 2 can be used to describe the number and the amplitudes of the disintegrated solitons in the wave packet.

In the experiments of Seabra-Santos et al.[14], the number of disintegrated solitons increases with the increase of the ratio between the step height and the water depth. In cases 32# and 33#, the wave breaking is observed when the ratio between the step height and the water depth reaches 0.67. Leading solitons break because of their relatively large amplitudes and the soliton amplitudes decline from the front to the rear of the wave packet. As shown in Table 2, the amplitudesof the disintegrated solitons are 1.72×10-2m,0.86×10-2m and 0.44×10-2m in case 32# and 2.18×10-2m, 1.10×10-2m and 0.56×10-2m in case 33#. Using the KdV model, the amplitudes of the third solitons in cases 32# and 33# are estimated to be 0.30×10-2m and 0.39×10-2m, respectively, which are similar to the values observed by Seabra-Santos et al..

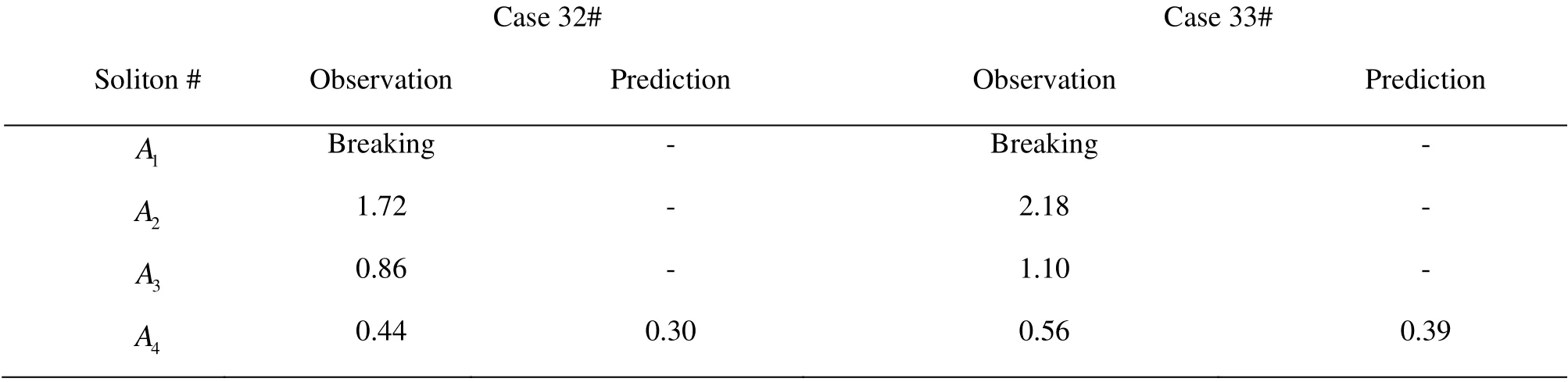
Table 2 Comparison of amplitudes of solitons obtained from experimental observations and model

Therefore, for a case that the leading solitons break,we can still use Eqs. (8), (13) and (15) to predict the number and the amplitudes of all subsequent solitons from the observed amplitudes of the first two unbroken solitons.

4. Conclusions

This paper studies the fission of both surface and internal solitary waves propagating over a variable topography by using the weakly nonlinear KdV equation. For the use of the previous KdV-type models, the input of the initial waveform of the incident solitary wave and the parameters of the water environment, including water depth and density stratification, is required to predict the outcome of the fission process. However, it is difficult to measure these parameters from the ocean because of their temporal and spatial variations. Moreover, although some achievements have been made in the measurement of solitary waves, the randomness of the waves makes it difficult to obtain the initial waveform.

We take a more practical approach and develop a model to use the amplitudes of the two leading solitary waves for predicting the number and the amplitudes of solitons in a wave packet. The number and the amplitudes of disintegrated solitons estimated by the model are close to those observed in experiments. For waves damping along the shelf, the model predictions are also in good agreement with numerical simulations by using a Navier-Stokes model in the range where disintegrated solitons are clearly visible. Through a theoretical analysis, we have further derived a version of the fission law that is applicable to internal solitary waves. Our analysis is validated by the data from the disintegration of two internal solitary waves as they propagate over a submerged seamount. The amplitudes of the third solitons as estimated by the model are qualitatively in good agreement with those obtained from space shuttle observations. The fission process in the case of wave breaking is also discussed. The agreement is also observed between the model predictions and the experimental observations in this particular case.

In summary, the derived fission law is practical and useful for describing the fission process of both nonbreaking and breaking solitary waves.