Some notes on numerical simulation of the turbulent cavitating flow with a dynamic cubic nonlinear sub-grid scalemodel in OpenFOAM*
Zi-yang Wang,Xian-bei Huang,Huai-yu Cheng,Bin Ji
1.State Key Laboratory of Water Resourcesand Hydropower Engineering Science,School of Power and Mechanical Engineering,Wuhan University,Wuhan 430072,China
2.Collegeof Electrical, Energy and Power Engineering,Yangzhou University,Yangzhou 225127, China
Abstract:The accuracy of largeeddy simulation (LES)ishighly dependent on the performance of sub-grid scale (SGS)model.In the present paper,a dynamic cubic nonlinear sub-grid scale model(DCNM) proposed by Huang et al. isimplemented for thesimulation of unsteady cavitating flow around a 3-D Clark-Y hydrofoil in OpenFOAM.Its performance in predicting the evolution of cloud cavitation is discussed in detail.The simulation with a linear model,the dynamic Smagorinsky model (DSM),is also conducted as a comparison.The results with DCNM show a better agreement with the available experimental observation.The comparison between DCNM and DSM further suggests that the DCNM is able to predict the backscatter more precisely,which is an important feature in LES. The characteristicsof DCNM isanalyzed to account for its advantagesin the prediction of unsteady cloud cavitation aswell. The results reveal that it is the nonlinear terms of DCNM that makes DCNM capture sub-grid scale vortices better and more suitable for studying the transient behaviors of cloud cavitation than DSM.
Key words:Cavitation,large eddy simulation (LES),nonlinear sub-grid scalemodel,OpenFOAM
Cloud cavitation is a special hydraulic phenomenon,which is characterized by complex phase-change, flow separation and multi-phase vortex structures[1-3]. It is ineluctable to induce vibration, noise and even material damage, which pose a major threat to the stability and efficiency of the hydraulic machineries.Therefore, much attention have been attracted to the mechanism of unsteady cloud cavitating flow[4-5].With
the great improvement of computer technology, large eddy simulation (LES), is attracting more and more interest with notable success in simulating cloud cavitation[6]. Long et al.[7] conducted a 3-D Lagrangian technique to provide an insight into the cavitating flows around a twisted hydrofoil. Ji et al.[8] researched into the transient cloud cavitation structures and cavitation-vortex interaction systematically.Wang et al.[9] analyzed the cloud cavitation characteristics over a Clark-Y hydrofoil using adaptive mesh refinement in OpenFOAM. However,the studies mentioned above all used the traditional sub-grid scale(SGS)models,which assumed a linear relationship between the SGS stress and the rate-of-strain.Tao et al.[10]pointed out that therewasa certain degree between the SGS stress and the eigenvectors of the strain rate tensor,which implies the need for the nonlinear SGS model to clarify the relationship between them more reasonably.Based on this theory,Huang et al.[11]developed a new nonlinear SGS model,namely dynamic cubic nonlinear model(DCNM).Different from the conventional nonlinear model with second-order term,this model contains a cubic term of the rate-of-rotation and the rate-of-strain tensors.Moreover,all the model coefficients are determined dynamically to ensure the accuracy of the calculation in predicting turbulence flow.This model has been successfully applied to the investigation of centrifugal pumps[12].However,the application of DCNM in the study of cloud cavitation is rarely reported.
Inspired by previous studies,the present paper numerically investigates the cloud cavitation around a Clark-Y hydrofoil using the DCNM in OpenFOAM.The DSM is also implemented as a comparison.The typical behaviors of cloud cavitation,the energy transmit process,especially the backscatter,are comparatively analyzed with DCNM and DSM.Then the advantages of DCNM in cloud cavitation simulation and the reason behind arediscussed.
The computational domain and the boundary conditions are shown in Fig.1,which are consistent with our previous study[9].InterPhaseChangeFoam is adapted to simulate cloud cavitation.Three sets of meshes,named Mesh 1-3,are generated with delicate refinement around the foil.The cell numbers of the three sets of meshes are about 1.44×106,2.88×106and 4.32×106,respectively.Figure 2 shows the grid distributions around the hydrofoil.It should be noted that the values of y+at the first grid point away from the hydrofoil surface are within 2,which fulfills the requirements of for+y for LES.
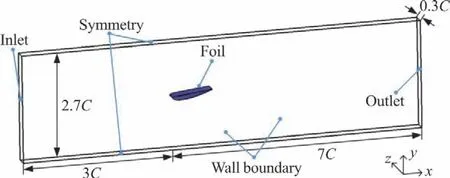
Fig.1 (Color online)Computational domain and boundary conditions
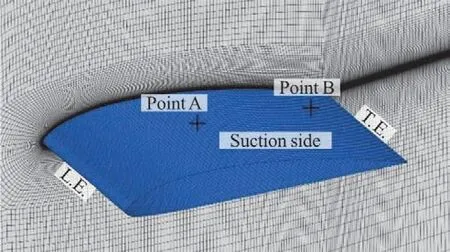
Fig.2 (Color online)Grid distributionsaround thehydrofoil
As shown in Table 1,the time-averaged lift coefficients and frequencies of cavity shedding simulated by meshes with different resolutions are compared with experiment data[13]. It is obvious that a better agreement between numerical and experimental results can be obtained with a higher mesh resolution.However,the differences between the results with mesh 2 and 3 are very minor and can be neglected.Considering the balance between computational cost and accuracy,mesh 2 isused asthefinal mesh.
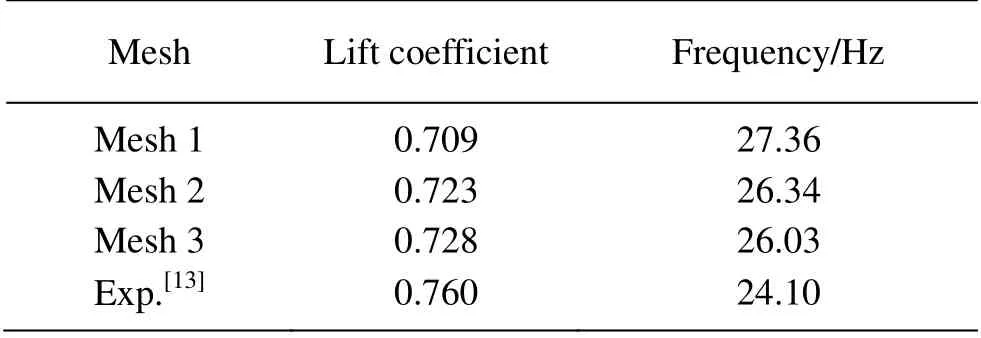
Table 1 Results of the mesh independence study
To compare the performance of DCNM and DSM in predicting the evolution of unsteady cloud cavitation, Fig. 3 presents six numerical snapshots in one typical cycle by two methods. The experimental results provided by Huang et al.[13] are also provided as a comparison. It is observed that both two models are capable of reproducing the inception, growth,shedding, convection and collapse of the cavities.However, DCNM captures the cavity structures at some instants better. Particularly, in Fig. 3(b), as marked by the red arrow, the DCNM successfully captures the U-shaped cavity in the wake, which was also reported by Huang et al.[13]. But the DSM fails to predict this feature. In Fig. 3(f), at this moment, the re-entrant jet cuts off the cavity interface and the large-scale cloud cavity is transported further downstream with the main flow. The size of the cloud cavity predicted by DCNM at t = 1.000T seems closer to the experimental observation when compared with that by DSM.

Fig.3 (Color online)Comparison of the side views of the isosurface of αv=0.1during one typical cycle with exp.[13],DCNM and DSM
In order to reveal the reason for the advantages of DCNM in the prediction of cloud cavitation,the backscatters,predicted by DCNM and DSM are compared in Fig.4.The backscatter is an important feature in LES,which means that the turbulent kinetic energy (TKE)transports from the filter scale to sub-grid scale. In other words, the negative value of TKE production represents the so-called backscatter.Figure 4 shows the variations of non-dimensional TKE production for DCNM and DSM at point A and B, whose locations are presented in Fig. 2. At point A,Fig. 4(a) indicates that though DSM captures the backscatter, its local pulsations are too violent, which may result in instability and failure of the numerical simulation[14]. Actually, as reported by Wang and Bergstrom[15], it is insufficient to perform the backscatter by only the linear term in DSM. Conversely,the DCNM avoids the problem of over-predicting backscatter. In DCNM, the backscatter is jointly calculated by three terms, which restrains the instability and pulsation of calculation. At point B, the DCNM captures more intense backscatter than that at point A,which can be attributed to the cloud cavitation. Actually,the shedding and collapse of cloud cavity produce much more sub-grid scale vortices which is captured by DCNM. It carries a large quantity of energy to the large eddies and thus generates intense backscatter. In contrast, there is only one linear term in DSM, which is not enough to capture sub-grid scale vortices and cannot take into full consideration the unsteady characteristics of the flow in the rear part of the foil. As a result, the predicted backscatter intensity by DSM is much lower than that by DCNM at point B.

Fig. 4 (Color online) Comparison of the backscatter at point A and B.

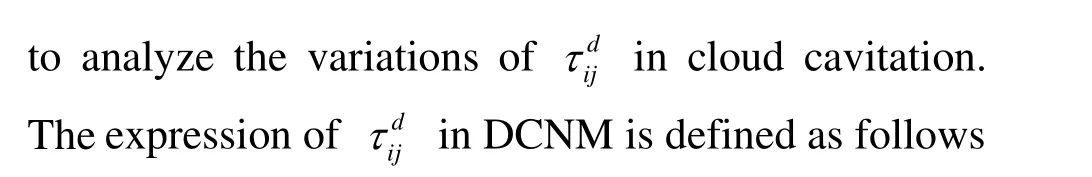

where the meaning of all parameters could be referred to our previous studies[11]. In DCNM, theis composed of three terms: the linear term Csterm and nonlinear terms C1and C2. According to our results, each component ofhas nearly identical variation trend, so only one component,is shown in the present paper. Figure 5 displays the variations of three terms of thein one typical cycle at point B. It is obvious that the nonlinear terms dominate this modeling process. Particularly, the C2term containing the cubic rate-of-rotation tensor fluctuates most violently, which implies that the C2term is crucial to capture transient behaviors and sub-grid scale vortices in cloud cavitation. Figure 6 shows three typical instants which are marked in Fig. 5. At instant I, velocity variation and the vortex structures can be identified by the local velocity vectors, which indicate that the flow in cloud cavity is very chaotic and significantly influences the stability of the region near point B. According to previous study[16], the process of cavity collapse involves vorticity production. So, it can be concluded that the fluctuation peak at Instant I is relevant to the collapse of the cloud cavity. Once the re-entrant jet generates and develops upstream, local flow patterns are modified. At Instant II, the point B is located in the region where the re-entrant jet meets the main flow.Figure 6(b) shows that the velocity changes drastically in this region. The interaction between the re-entrant jet and the main flow induces many small-scale vortices, which are mainly modelled by the C2term and cause the distinct fluctuations of the curve in Fig.5. Chen et al.[17]pointed out the sweeping effect of the re-entrant jet strengthened the local turbulence intensity. So, at instant II, the development of the re-entrant jet is responsible for the fluctuation peak of the curves. At instant III, the attached cavity is pinched off by the re-entrant jet and the cavity structures are highly irregular.It can beseen from Fig.6(c)that the point B is in cloud cavitation region and two distinct vortices are visualized,which indicate that the local flow field is very complex.Similar with the situation at instant II,this region is affected by both re-entrant jet and the main flow, which makes the curves fluctuate frequently.In brief,due to the existence of nonlinear terms,especially the2C term,DCNM is capable to precisely capture the sub-grid scale vortices and more suitable for studying the transient behaviorsin cloud cavitation.
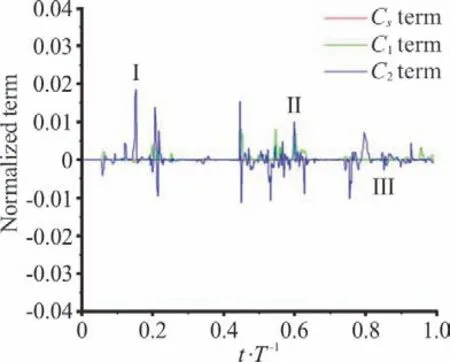
Fig.5 (Color online) Variations of three terms of τ 1d1in DCNM in onetypical cycleat point B
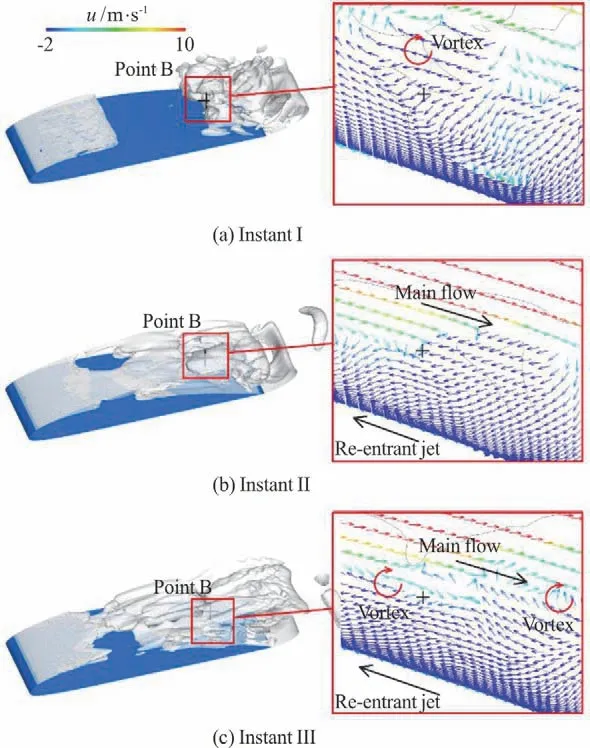
Fig.6 (Color online)Cloud cavitation structures and local velocity vectorsnear Point Bon plane z / c=0.15 at three instants by DCNM
In this paper,the unsteady cavitating flow around a Clark-Y hydrofoil is investigated using a dynamic cubic nonlinear SGS model(DCNM)in OpenFOAM.Special emphasis is put on the thorough analysis of the advantages of DCNM in cloud cavitation prediction and the reason behind.The main conclusions are summarized asfollows:
(1)Compared with DSM,the DCNM shows a better agreement with the experimental observation and presents much more flow details,such as the U-shaped cavity in the process of cloud cavity collapse.
(2)DCNM demonstrates its flexibility and stability to predict backscatter and avoid the potential excessive reverse energy transmit process.The nonlinear terms in DCNM are crucial to the prediction of the backscatter in cloud cavitation.In the cavity shedding region,the DCNM captures more sub-grid scale vorticesand presentsmore intense backscatter.
(3)Combing with the evolution of cloud cavitation,the reason behind for the advantages of DCNM is analyzed systematically.The nonlinear terms of DCNM plays a dominant role in capturing the transient behaviors of cloud cavitation.The development of the re-entrant jet and the collapse of the cloud cavity are the primary mechanism of fluctuation peaks of the nonlinear termsin DCNM.
 水動(dòng)力學(xué)研究與進(jìn)展 B輯2020年4期
水動(dòng)力學(xué)研究與進(jìn)展 B輯2020年4期
- 水動(dòng)力學(xué)研究與進(jìn)展 B輯的其它文章
- Development and application of a new random walk model to simulate the transport of degradablepollutants*
- Predictions of bulk velocity for open channel flow through submerged vegetation*
- On solitary wave in nonuniform shear currents *
- Fission law of solitary waves propagating over sharply variable topography *
- A TensorFlow-based new high-performance computational framework for CFD *
- Experimental investigation of wall-bounded turbulence drag reduction by active control of double piezoelectric vibrator *
