Chi-Shung YIP (葉孜崇), Wei ZHANG (張煒), Guosheng XU (徐國(guó)盛) and Noah HERSHKOWITZ

1 Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, People’s Republic of China

2 Department of Engineering Physics, University of Wisconsin-Madison, Madison, WI 53706, United States of America

Abstract An algorithm for automated fitting of the effective electron temperature from a planar Langmuir probe I-V trace taken in a plasma with multiple Maxwellian electron populations is developed through MATLAB coding.The code automatically finds a fitting range suitable for analyzing the temperatures of each of the electron populations. The algorithm is used to analyze I-V traces from both the Institute of Plasma Physics Chinese Academy of Sciences’s Diagnostic Test Source device and a similar multi-dipole chamber at the University of Wisconsin-Madison.I-V traces reconstructed from the parameters fitted by the algorithm not only agree with the measured I-V trace but also reveal physical properties consistent with those found in previous studies.Cylindrical probe traces are also analyzed with the algorithm and it is shown that the major source of error in such attempts is the disruption of the inflection point due to both decreased signal-to-noise ratio and greater sheath expansion. It is thus recommended to use planar probes with radii much greater than the plasma Debye length when signal-to-noise ratio is poor.

Keywords: EEDF, Langmuir probes, plasma diagnostics

1. Introduction

Since their introduction by Irving Langmuir [1], Langmuir probes are arguably the most important plasma diagnostic.They are widely used in fusion research[2,3]and in low temperature plasmas[4-8].They provide a simple,robust,cost effective,and relatively accurate way to measure key parameters including the electron temperatureTe, electron densityne, and sometimes the plasma potentialVp. As measurements are performed through directly collecting electrons of selected energies, Langmuir probe measurements do not require the assumption of the electron energy distribution functions (EEDFs) being single Maxwellian. The assumption of the diagnosed plasma having a single Maxwellian EEDF is often required by cutoff frequency measurements and optical diagnostics[9]which do not return an electron energy spectrum. Because a Langmuir probe directly measures the EEDF through selective absorption of electrons with the probe’s bias,it also has the almost unique advantage of diagnosing plasmas with complex EEDFs like double Maxwellian and triple Maxwellian distributions [10]as well as plasmas with electron and ion beams.

Arguably the most physically accurate analysis of Langmuir probeI-Vcharacteristics is to extract the measured EEDFs through differentiating theI-Vtrace twice [11](or once when the diagnosed plasma is strongly magnetized[12]). This, however, is often unrealistic for probes in noisy environments as any noise will become amplified when each derivative is calculated. In addition, virtual cathodes near large probes and/or potential distortion by contaminated probe surfaces tend to disrupt theI-Vtraces near the plasma potential [13-15], causing d2I/dV2to become distorted.These problems are visually demonstrated in figure 1.

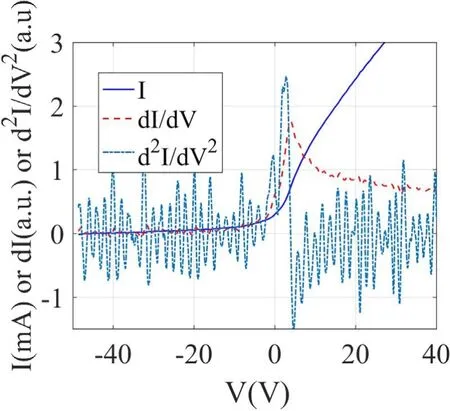
Figure 1. dI/dV and d2I/dV2 of a noisy Langmuir probe trace. The high frequency noise is amplified with each derivative.

An alternative procedure is to fit theI-Vcharacteristics assuming some form of EEDFs. Since information regarding the EEDF is not physically lost in the data acquisition process, one can choose the form of the EEDFs that best fits theI-Vtrace.This is important as most linear devices are known to create at least two species of electrons:a hot species created through electron heating by the plasma source, and a cold species created through ionization of neutral gas. Limited confinement in these devices prevents electrons from totally thermalizing, so electrons created from these different mechanisms remain separate Maxwellian distributions spatially overlapping each other.In these plasmas the ability to fit multiple Maxwellian distributions is thus an important way to understand the EEDFs and the mechanism behind their formation in these devices.Traditionally double Maxwellian and triple Maxwellian EEDFs are fit by manually [16]determining the portion of theI-Vtrace most suitable to fit a straight line with theI-Vtrace drawn on a semi-log graph. This method is adequate if there are only a few Langmuir probe traces per experiment to be analyzed, but becomes very tiresome and prone to human error if,for example,a spatial or temporal distribution of parameters is needed which can require dozens or even hundreds of traces to be analyzed from each experiment [17]. Commercially available Langmuir probes generally come with automated fitting of single Maxwellian EEDFs,but not double Maxwellian EEDFs.This is due to the difficulty in automating the determination of a suitable fitting range of the hotter species of electrons.In this work,we present a procedure to automate single Maxwellian,double Maxwellian and triple Maxwellian fitting of Langmuir probeI-Vtraces with fitting ranges automatically selected through repeated and iterative fitting.

2. Experimental setup

The fitting algorithm presented in this work is used to analyzeI-Vtraces from the Diagnostics Test Source (DTS) at the Institute of Plasma Physics in Hefei, China, as well as those from the multi-dipole filament discharge device at the University of Wisconsin-Madison, USA, described elsewhere [10].

The DTS multi-dipole confined plasma device consists of a 25 cm diameter, 60 cm long vacuum chamber. Multi-dipole confinement was invented by Limpaecher and Mackenzie and its detailed working principles can be found in[18].Plasma is produced through impact ionization from primary electrons produced by two 12 cm long, ohmically heated tungsten filaments located near the end wall, emitting the discharge currentIDis.In this experiment we employ argon gas to produce a plasma consisting of positive ions and electrons. 16 rows of permanent magnets surround the radial wall, providing multidipole confinement resulting in a uniform plasma [18]. A schematic of the setup is presented in figure 2.

A radially movable Langmuir probe is employed to measure the electron temperatureTe, the plasma densityne,and the local potentialVp. The movable range of the probe spans the chamber’s diameter. The planar Langmuir probe employed in this experiment is constructed with a 0.2 mm thick, 8 mm diameter tantalum disc spot welded onto a 0.8 mm diameter copper plated stainless steel wire, covered by a 2 mm diameter single holed ceramic tube connecting it to the 4 mm diameter stainless steel probe shaft. For the cylindrical probe, a 0.15 mm diameter, 19 mm long tungsten wire is fitted into a 0.8 mm copper tube covered by a single holed ceramic tube connected to an identical shaft. Figure 3 shows a schematic of the probe tips.

3. Iterative fitting process

A MATLAB code is developed for the iterative Langmuir probeI-Vtrace fitting process, described below. The flow charts of single Maxwellian, double Maxwellian and triple Maxwellian fittings are illustrated in figures 4-6 respectively.These automated fitting processes were developed from previous ones in which the fitting ranges were determined manually [16], as described below.

The first step of the single Maxwellian fitting process is to fit a straight line to the ion-saturation currentIisdata over a 10 V range, beginning with the minimum voltage, as illustrated in figure 7(a).Iiswill be subtracted from theI-Vtrace and theIissubtracted trace will be used for all three fitting processes. The trace is then preliminarily fitted for the electron temperatureTe1in the fitting range of (Vinf-1 V) ＜V＜Vinf,whereVinfis the inflection point voltage.The region nearVinf, being near the plasma potentialVp, corresponds to both the maximum slope and the lowest energy part of theI-Vtrace, i.e., the coldest electron species in theI-Vtrace for a multiple Maxwellian EEDF plasma. In this work, we have chosen an effective electron temperatureTeff= 1/Σs(ns/(neTs)),wherensandTsare the density and temperature of the Maxwellian electron populations. This effective temperature,weighed towards colder electron species, determines the Bohm velocity as well as the ion acoustic speed in a plasma with multiple Maxwellian EEDFs[19,20].In addition,Vinfis not taken as the plasma potentialVpa priorieven when assuming a non-drifting Maxwellian EEDF,as effects alteringVinfincluding contaminated probe surfaces and the formation of virtual cathodes nearVpare not automatically dismissed [13, 15].

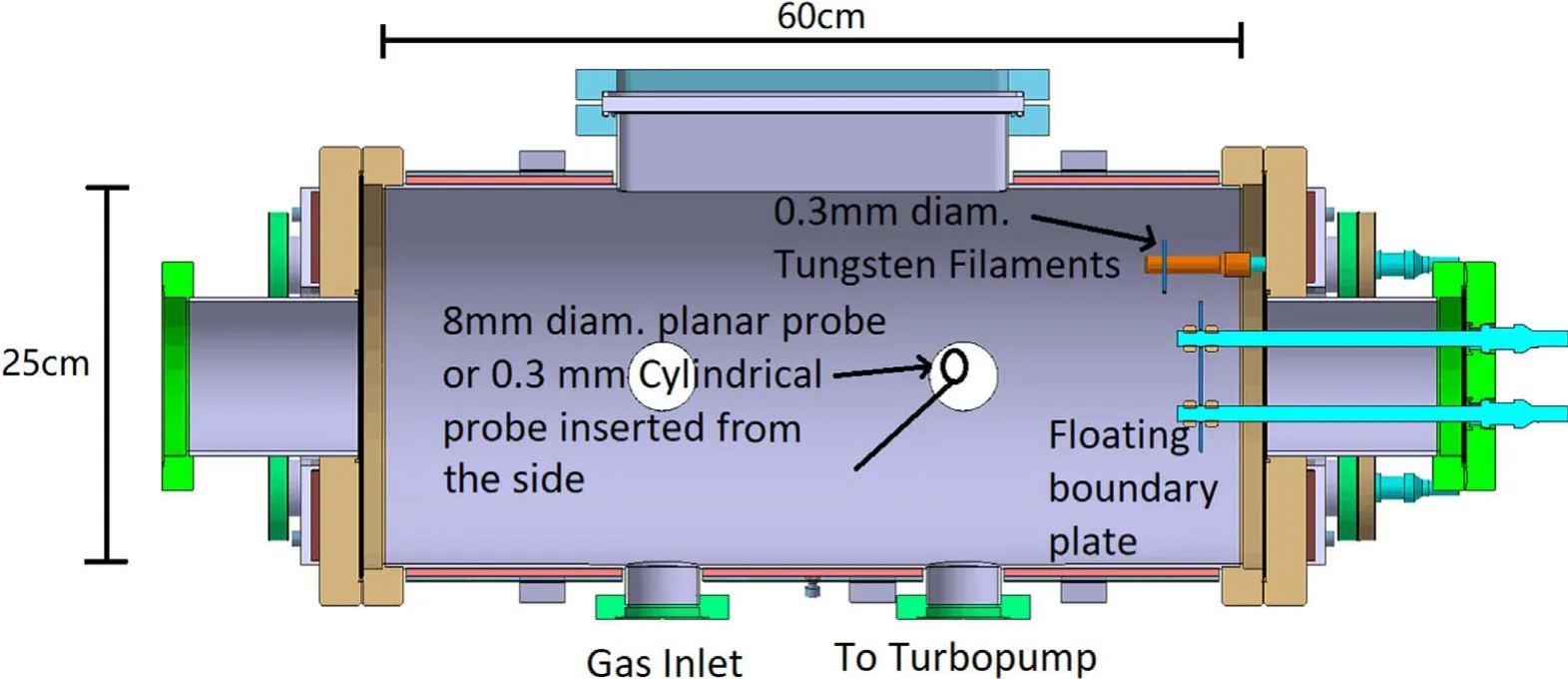
Figure 2. Schematic of DTS.

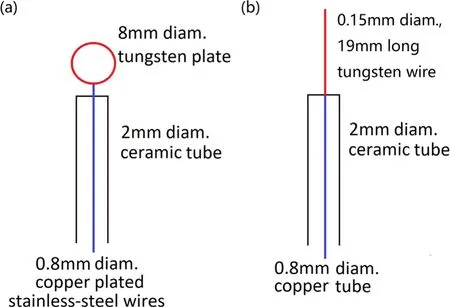
Figure 3. Schematics of the (a) planar Langmuir probe, and the(b) cylindrical Langmuir probe.

The fitting process ofTe1is repeated using the resultantTe1to determine the fitting range(Vinf-Te1/e) ＜V＜Vinffor the next iteration, untilTe1converges within 0.05 eV of its previous iteration.This allows the final fitting range forTe1to be determined by the EEDF itself,consistently giving fitting a range of 63% of the lowest energy electrons in the EEDF no matter whatTeis, if the EEDF is single Maxwellian. This is because atTe/ebelow the plasma potential, the probe repels approximately 37% of the electrons according to the Boltzmann relation, thus using the proportion of theI-Vtrace aboveV=Vp?Te/eincludes the contribution of 100%-37% = 63% of the electrons from a single Maxwellian EEDF.

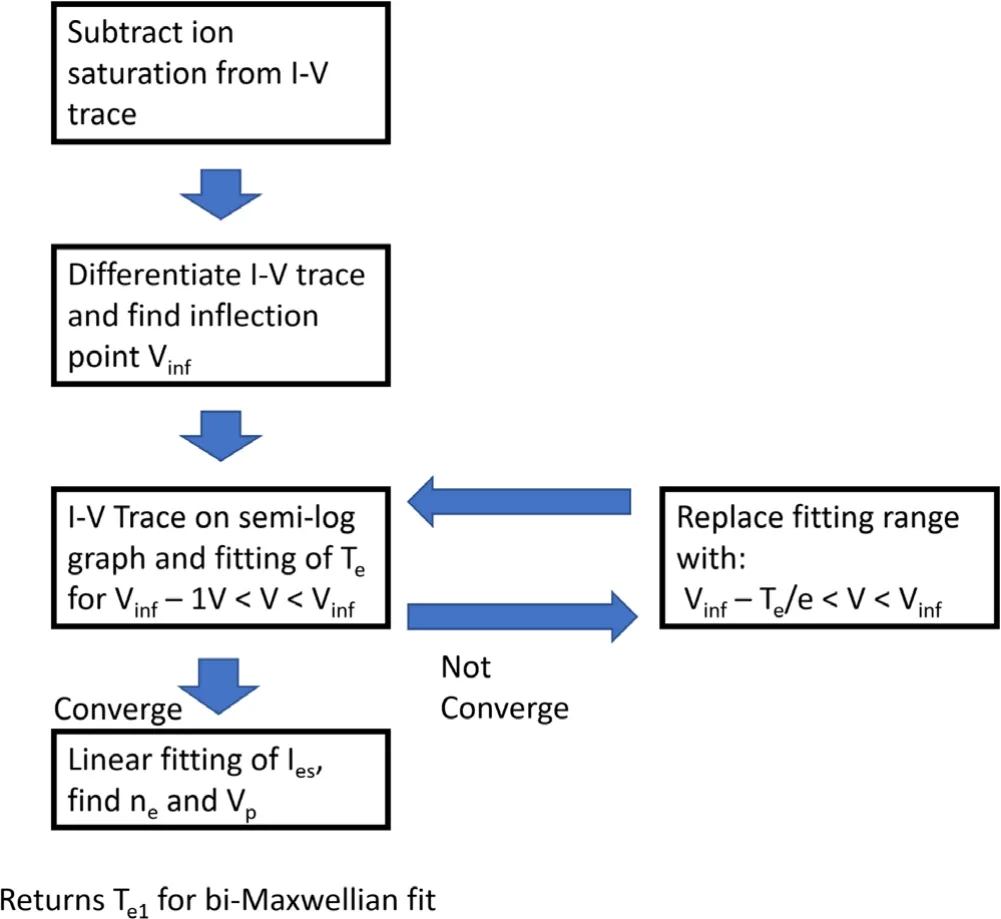
Figure 4.Flow chart for the single Maxwellian fitting algorithm.

Electron saturation is then linearly fitted [21]over the fitting range (Vinf+ 5 V) ＜V＜ (Vinf+ 10 V), and an interception with the exponential fitting ofTe1extended beyondVinfis taken asIesandVpassuming a non-drifting EEDF. The 5 V voltage range immediately afterVinfis excluded from the fitting range to prevent virtual cathode and surface contamination effects being confused with electron saturation. For simplicity, the change of the probe’s effective area due to sheath expansion is approximated to increase linearly with the probe bias, and so does the saturation current. Since this is not always the case [22, 23], choosing a fitting range close toVpcan improve accuracy. If a probe is found to be sufficiently cylindrical,i.e.the radius of the proberprobeis much smaller than the Debye length λDebye, then the interception method is inappropriate [21]. In that case,Vinfwill be taken asVpfrom which the electron saturation currentIesand the electron densityneis calculated from theI-Vtrace.This is determined through two criteria:either the resultantVpis smaller thanVinf, or the resultantIesis smaller than the measured currentIinfat the interception point. These criteria are used because virtual cathode and surface contamination effects can reduce theVinfandIesbut not increase them [13, 15].

Figure 5.Flow chart for the double Maxwellian fitting algorithm.

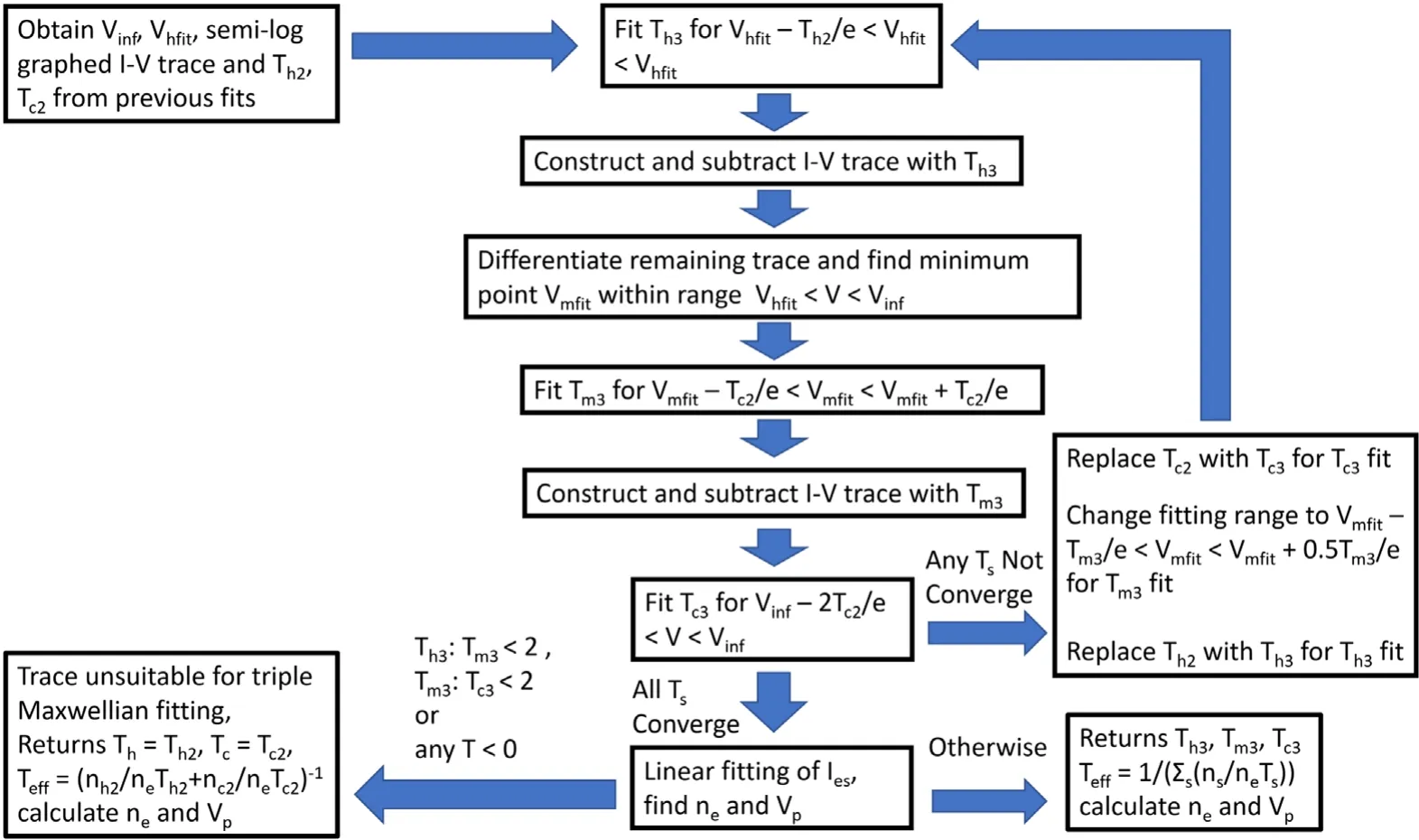
Figure 6. Flow chart for the triple Maxwellian fitting algorithm.

Parameters from the single Maxwellian fitting are then used to fit a double Maxwellian EEDF to theI-Vtrace withIissubtracted. One should note that forI-Vtraces with multiple Maxwellian EEDFs,the contribution from the colder electron population reduces more rapidly than the contribution from the hotter ones as voltage decreases, as a direct result of the Boltzmann relation. This effect favors a fitting procedure of multiple Maxwellian EEDFs that starts with fitting and subtracting the hottest population because the hotter populations can be separated from the colder ones simply by selecting a very negative region on theI-Vtrace [24]. To ensure fitting for the hottest population on theI-Vtrace, the ln(I) is differentiated and the voltage pointVhfitwith the minimum absolute value of |d(ln(I))/dV| is found within the range ofV＜Vinf. ThenTh2is fitted in the range ofVhfit-10 V ＜V＜Vhfit.The 10 V fitting range is a seeding value which will be replaced byTh2/ein subsequent iterations, and the choice ofVhfitreflects the region of theI-Vtrace that can be fitted with the maximum temperature.This avoids a region where a poor signal-to-noise ratio results in the current fluctuating across zero, with the ln(I) exploding negatively, corresponding to falsely cold temperatures. A hypotheticalI-Vtrace is then constructed beyond the inflection pointVinfwith this fittedTh2to be subtracted from the actualI-Vtrace. This range selection and fitting process is illustrated in figure 7(b).Then the temperature of the cold electron populationTc2is determined from the remainingI-Vtrace in the fitting range ofVinf-Te1/e＜V＜Vinfon a semi-log graph, as illustrated in figure 7(c). The fitting process forTh2andTc2is then reiterated with theTc2fitting range beingVinf-Tc2/e＜V＜Vinfand theTh2fitting range beingVhfit-Th2/e＜V＜Vhfit,untilTh2andTc2converge to values within 1%. Several conditions render theI-Vtrace unfit for double Maxwellian fitting and terminate the program, returningTe=Te1: eitherTh2＜Tc2,or if a negative temperature appears in any iteration, or the finalTh/Tc＜ 1.7. These conditions remove unphysical results and cases where the two temperatures are not sufficiently different such that their fitting ranges might overlap,in which case theI-Vtrace will be best approximated by a single Maxwellian EEDF.

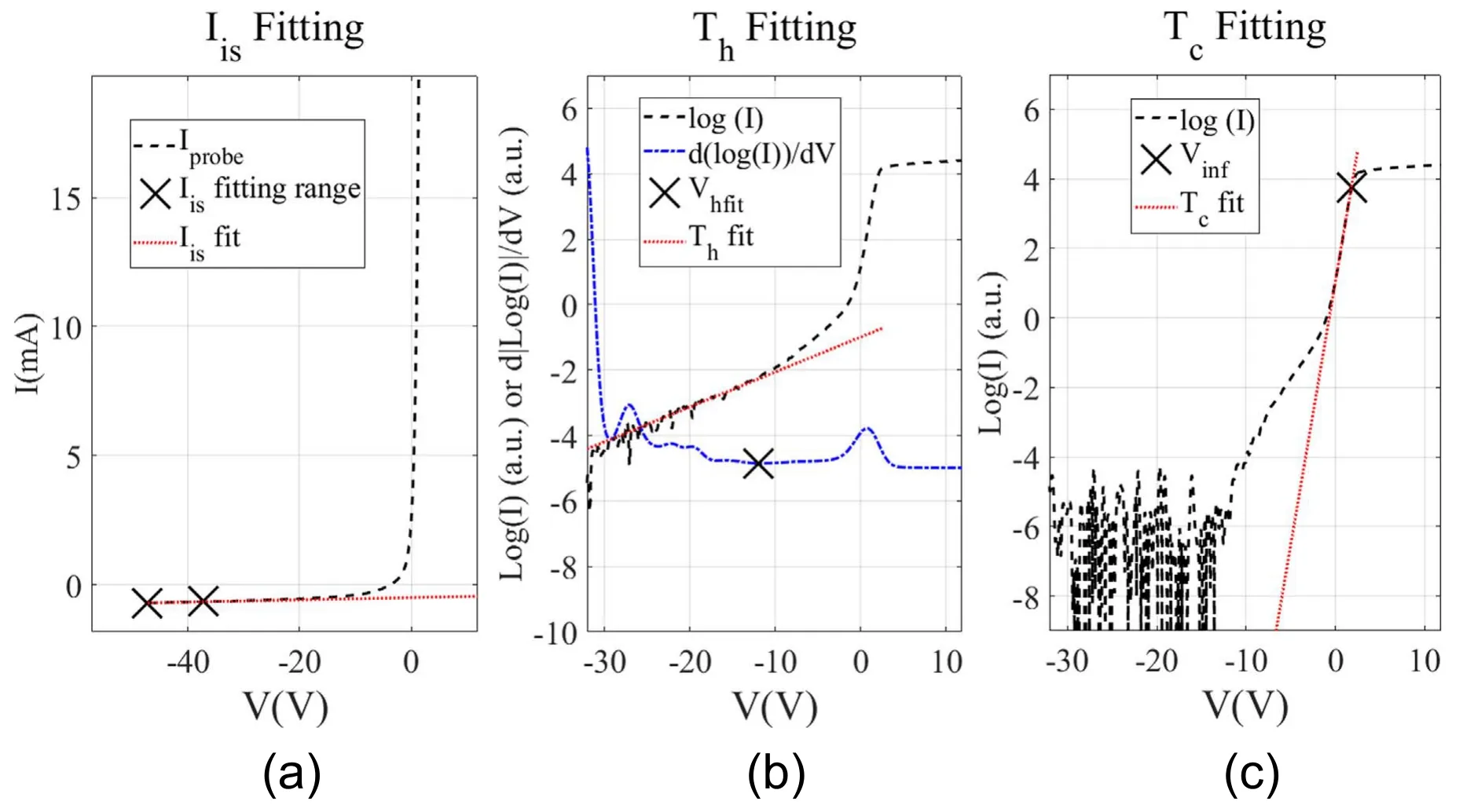
Figure 7.Determining the fitting range for Iis (a), Th (b) and Tc (c) after the current contribution from the hot electron population has been subtracted.I-V trace is measured in the DTS device with 0.38 Pa argon neutral pressure and discharge current of IDis = 0.5 A.The fitted Iis,Th and Tc are reconstructed with the red dotted line.

If the fitting process returns validTh2andTc2, a hypothetical trace constructed with both the electron populations will then be drawn to find its intercept with the linearly fitted electron saturation current,from which the density of the cold populationnc2, that of the hot populationnh2and the total densityne2=nc2+nh2will then be calculated.

Plasmas are not always best described by double Maxwellian EEDFs. In some plasmas like multi-dipole confined filament discharges, however, the ‘mid-temperature’secondary electrons from the walls are sufficiently different from degraded primaries and plasma electrons produced by ionization so that they forming three electron species plasmas.There is thus a need for an in-depth analysis of their EEDFs [10].

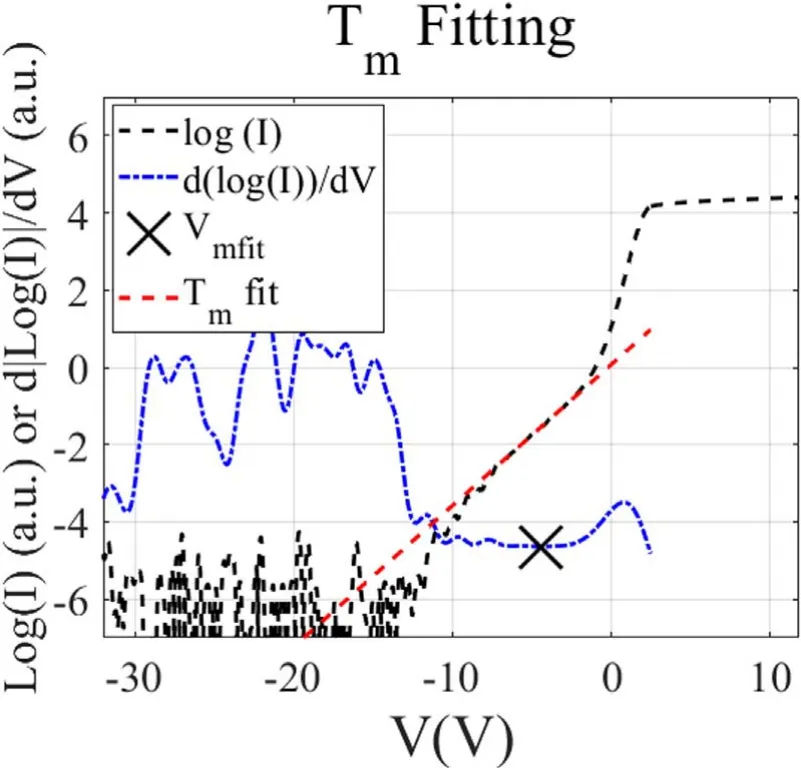
Figure 8.Determining the fitting range for Tm for the same I-V trace as figure 7, after current contribution from the hot electron population has been subtracted.

The triple Maxwellian fitting process is similar to the double Maxwellian one, but with an additional step of fitting and subtracting a ‘mid-temperature’ population from theI-Vtrace between the fitting process ofTh2and that ofTc2.This is done by natural logging and differentiating theI-Vtrace to find a second minimum pointVmfitwith the rangeVhfit＜V＜Vinf. Then the temperature of the ‘mid-temperature’ populationTm3will be fitted in the range ofVmfit-Tc2/e＜V＜Vmfitfor the first iteration and with the rangeVmfit-Tm3/e＜V＜Vmfitfor subsequent ones. This process is illustrated in figure 8. With triple Maxwellians the fitting range of the temperature of the coldest electron speciesTc3can be extended toVinf-2Tc2/e＜V＜Vinf, as subtraction of the hotter species reduces their distortion to the fitting of the coldest one.Fitting is again re-iterated,Th3,Tm3andTc3replacingTh2andTc2untilTh3,Tm3andTc3converge to 1%.IfTh3/Tm3＜ 1.7 orTm3/Tc3＜ 1.7,or if a negative temperature appears in any iteration, then triple Maxwellian fitting is invalid and the program shall returnTeff= (nc2/(neTc2) +nh2/(neTh2))?1. Otherwise, anI-Vtrace will be constructed with all three electron populations to obtainIesas described above. The effective electron temperature will be given byTeff= (nc3/(neTc3) +nm3/(neTm3) +nh3/(neTh3))?1, wherenc3,nm3,nh3are densities calculated by using the current value on their respective hypotheticalI-Vtraces atVpandne=nc3+nm3+nh3.

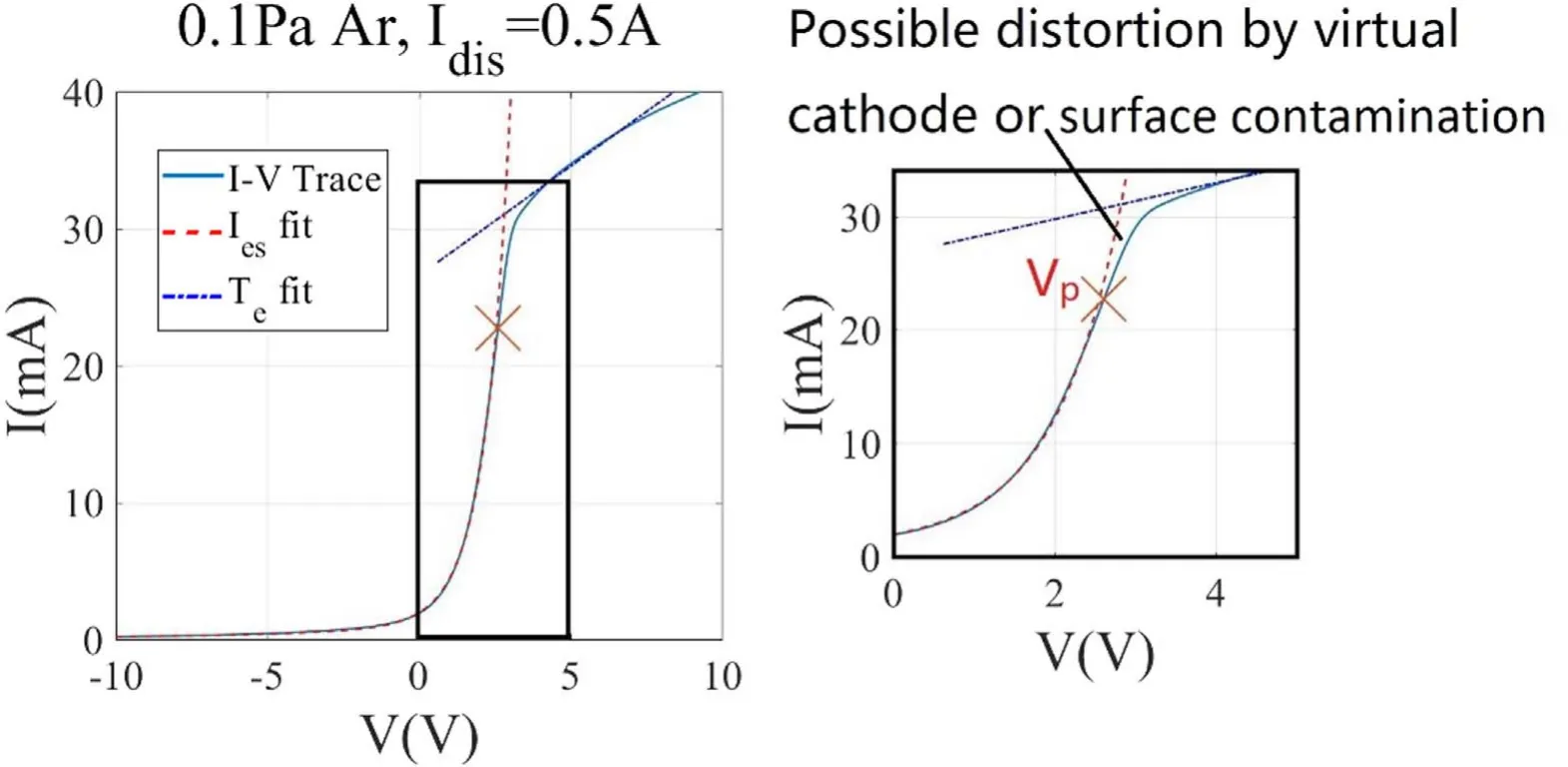
Figure 9. A Langmuir probe I-V trace (cyan solid line) from the DTS device automatically fit with the triple Maxwellian procedure (red dashed line). In this plasma, measured parameters are Teff = 0.83 eV and ne = 1.2 × 1010 cm?3.

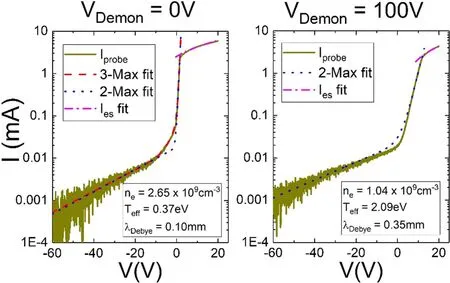
Figure 10.Double Maxwellian(2-Max)and triple Maxwellian(3-Max)fitted Langmuir probe traces from the multi-dipole filament discharge at the University of Wisconsin-Madison, with VDemon = 0 V (a) and VDemon = 100 V (b). Measurements are taken in a 0.4 Pa argon discharge with 0.3 A discharge current.

After each fitting process is completed, anI-Vtrace constructed using the parameters from the fitting process will be displayed on both linear and semi-log graphs, along with the measuredI-Vtrace for the user to inspect the validity of the automated fitting.

4. Experimental results

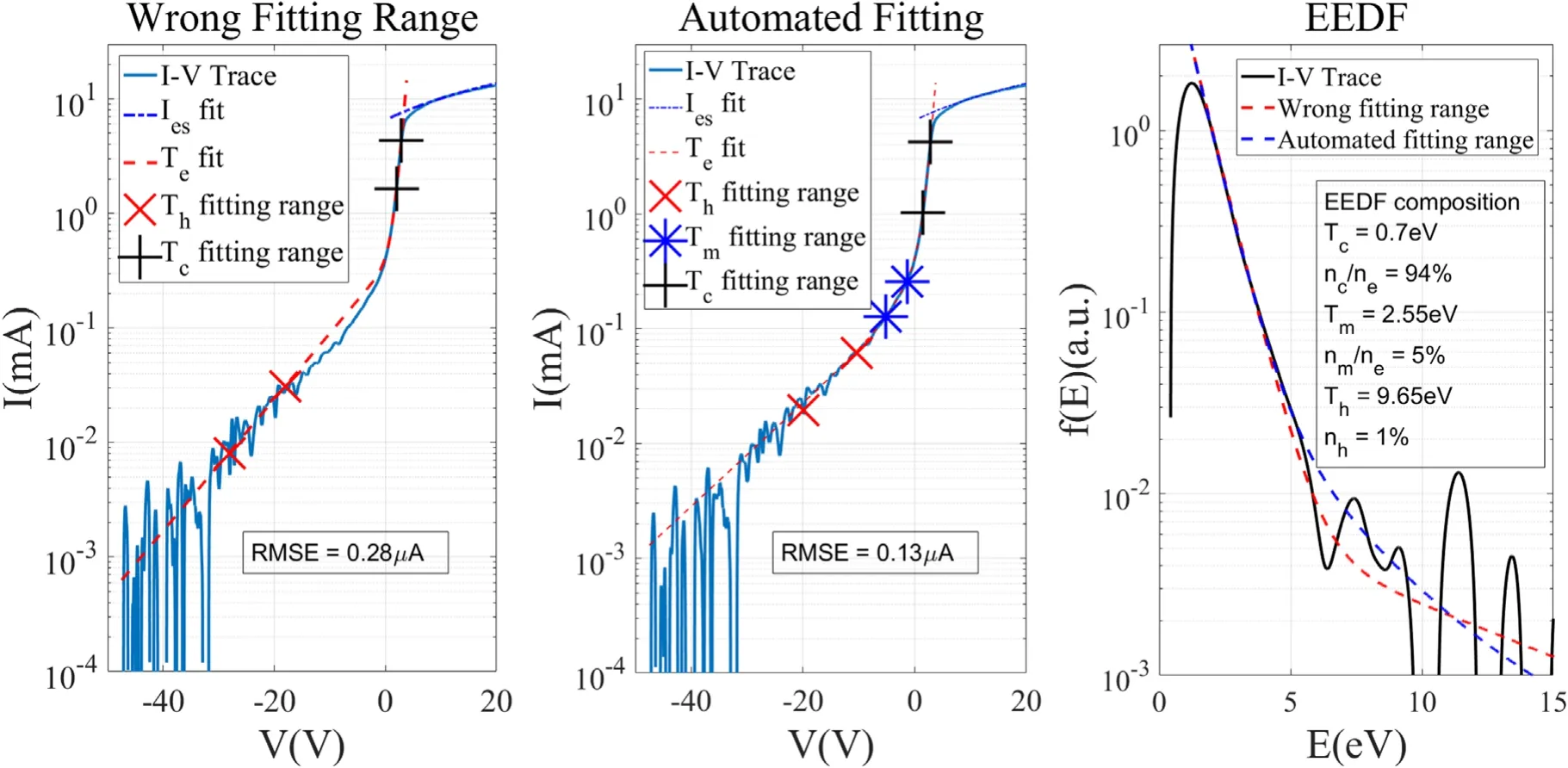
Figure 11.I-V traces taken in a 0.05 Pa, IDis = 0.2 A argon discharge in the DTS device fitted with incorrect and correct fitting ranges.Measured parameters are Teff = 0.73 eV, ne = 3.2 × 109 cm?3 and λDebye = 0.13 mm.

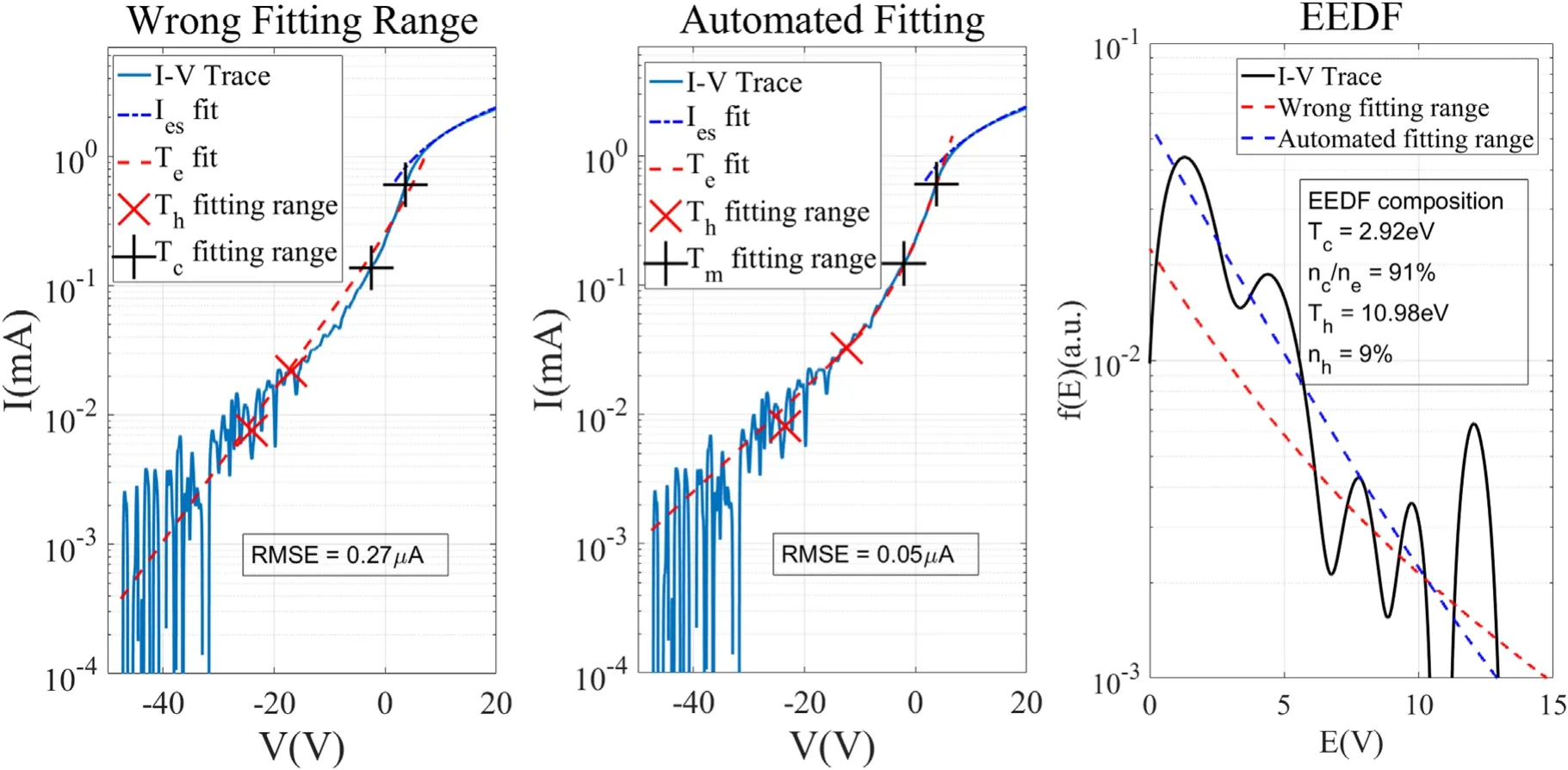
Figure 12.I-V traces taken in a 0.005 Pa, IDis = 0.2 A argon discharge in the DTS device fitted with incorrect and correct fitting ranges.Measured parameters are Teff = 3.1 eV, ne = 1.8 × 108 cm?3 and λDebye = 0.93 mm.

Figure 9 shows a Langmuir probe trace measured in a DTS discharge at 0.1 Pa argon neutral pressure and 0.5 A discharge current with its ion saturation current subtracted. Reconstruction of theI-Vtrace through automated triple Maxwellian fitting shows good agreement with theI-Vtrace until approximately 0.5Te/enearVp. This portion of theI-Vtrace is known to be affected by virtual cathodes and surface contaminations [13-15]. It is unlikely that this relatively slight flattening reflects a real transition to saturation since the current still increases by more than 20% (22.7 mA versus 27.4 mA) within 0.16Te/ebefore flattening at the characteristic ‘knee’ of theI-Vtrace of a planar probe. This issue,consistent with previous studies, is the reason whyVinfandIinfare not immediately selected as the plasma potential and the saturation current respectively.The interception technique and the inflection point can result in an approximately 10%disagreement inVp(2.61 V versus 2.88 V) but a 40% disagreement inIes(22.7 mA versus 31.2 mA).

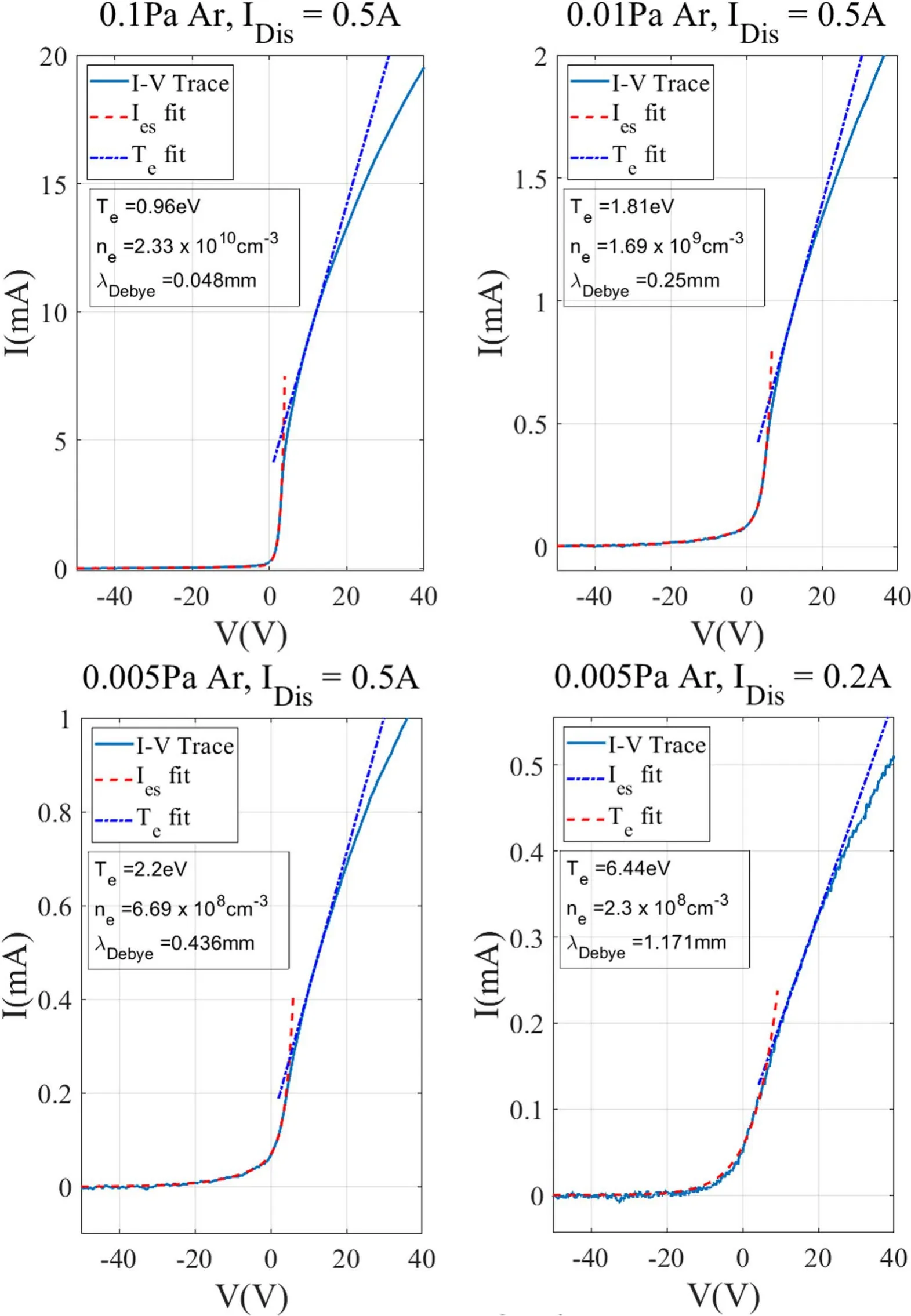
Figure 13.I-V traces of a cylindrical probe with decreasing neutral pressures and discharge currents.

I-Vtraces from the University of Wisconsin-Madison’s multi-dipole filament discharge with and without a Maxwell Demon [5, 10]turned on were analyzed using the fitting algorithm to test its effectiveness. When the Demon is turned off, a ～0.4 Pa argon multi-dipole confined filament discharge usually exhibits three Maxwellian electron populations:degraded primary electrons,secondary emitted electrons from the walls, and ionization electrons. With increasing bias on the DemonVDemon,the triple Maxwellian EEDF is eventually reduced to a double Maxwellian EEDF with only the degraded primaries and a ‘cold’ population with its temperature at or above that of the secondary electrons from the walls [10, 16]. Figure 10 shows twoI-Vtraces, with their ion saturation current subtracted, in such plasma with theVDemon= 0 V andVDemon= 100 V. As shown in the figure, the algorithm reconstructed both traces with triple and double Maxwellian EEDFs with good agreement matching both traces. The algorithm also determined that theVDemon= 100 V trace is not suitable for triple Maxwellian fitting as it detected a meaningless negativeTc3, which is usually due to a lack of significant signal for the fitting process to iterate. It should also be noted that in theVDemon= 100 V case, mid-energy electrons are depleted as the Demon raises the electron temperature to a point where electrons that form the population’s tail are non-existent. This is consistent with previous studies [10, 16].

Figure 11 demonstrates the significance of determining the correct fitting range for both cold and hot electron populations. It shows a planar Langmuir probe trace in a 0.05 Pa, 0.2 A plasma, with its ion saturation current subtracted, that has been deliberately fitted with an incorrect fitting range for the degraded primary electron population and with the automated algorithm. As shown in the figure, fitting the trace with an incorrect fitting range causes the density of the degraded primary electron population to be overestimated,which in turn causes the mid-temperature population to become undetectable. When the signal-to-noise ratio is poor,this effect can be more profound, as shown in figure 12, in which another planar Langmuir probe trace in a 0.005 Pa,0.2 A plasma is similarly fitted with incorrect and automated fitting ranges. One can see that the reconstructedI-Vtrace severely mismatches the measuredI-Vtrace. In these cases,the fitted temperature is not a reliable estimate ofTe.

Figure 13 shows a series ofI-Vtraces obtained using a 0.15 mm diameter, 19 mm long cylindrical Langmuir probe for various neutral pressures and discharge currents,with their ion saturation currents subtracted to facilitate electron temperature fitting.When the Debye length λDebyeis much smaller than the probe’s radiusrprobe, the probe behaves as a planar probe even when it is cylindrical,as sheath expansion is small compared torprobe. As neutral pressure and discharge current decrease,nedecreases and thus the Debye length increases.As shown in figure 13, as λDebyebecomes much longer thanrprobe,the probe starts to behave as a cylindrical probe.This is signified by the ‘knee’of theI-Vtrace becoming less clear as neutral pressure andIDisdecrease. If a significant portion of the noise comes from outside the plasma, reducingnealso reduces the signal-to-noise ratio as the probe’s collected current decreases. This reduction of signal-to-noise ratio can affect cylindrical and spherical probes(rprobe? λDebye)more significantly because their electron saturation currents grow much steeper than that of a planar probe due to sheath expansion effects. This results in increased dI/dVbeyondVpwhich affects the determination ofVinf. This is illustrated in figures 13 and 14. Note that in figure 14 the smoothedI-Vtrace, used to produce dI/dV, almost overlaps the rawI-Vtrace. In this plasma,rprobe/λDebyeis between 1/10 to 1/15 for the cylindrical probe, which ensures that the probe is sufficiently cylindrical with respect to the plasma. A fitting with a manually selected lowerVinf, shown in figure 15, is a notably better fitting to theI-Vtrace despite all other fitting parameters still being determined automatically. This also shows why using cylindrical probes is often unfavorable under low signal-to-noise situations. Should cylindrical probes be used in these situations,using an emissive probe to determine the correctVpwill result in much betterTefitting,but only when global electron flows are absent.Note that one can always obtain a fitted parameter if one smooths theI-Vtrace enough for the fitting algorithm to find a consistent result, but the physical information of theI-Vtrace is gradually lost through smoothing.Thus,the acceptable signal-tonoise ratio is dependent on the degree of error acceptable to the user of the algorithm. TheI-Vtrace shown in figures 13(d)and 14 has a noise to electron saturation current ratio of approximately 1:10 before smoothing, which would be close to the minimum acceptable signal-to-noise ratio for the purpose of this work.

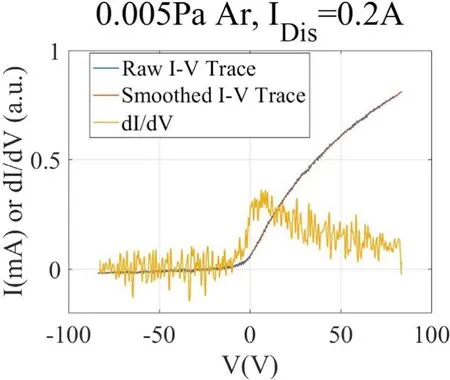
Figure 14.A cylindrical probe I-V trace and its derivative of a 0.005 Pa, IDis = 0.2 A argon plasma.

Also shown in figure 15 is an automatically analyzedI-Vtrace of a planar probe in a similar discharge. The planar probe is almost immune to the issue of theVinfbeing unclear as its transition to electron saturation is much more pronounced due to reduced sheath area expansion relative to the probe’s area.The planar probe trace also shows a clear double Maxwellian distribution, due to increased signal-to-noise ratio. Note that a probe is physically cylindrical only whenrprobe? λDebye, with typical cylindrical probes constructed with 0.15 mm diameter tungsten wires. This means that for plasmas withne＞ 109cm?3andTe≈ 1 eV,these probes are unlikely to be affected by the effects portrayed in figure 14 as they physically behave like planar probes,even when they are cylindrical. However, they not directional probes.

5. Conclusion

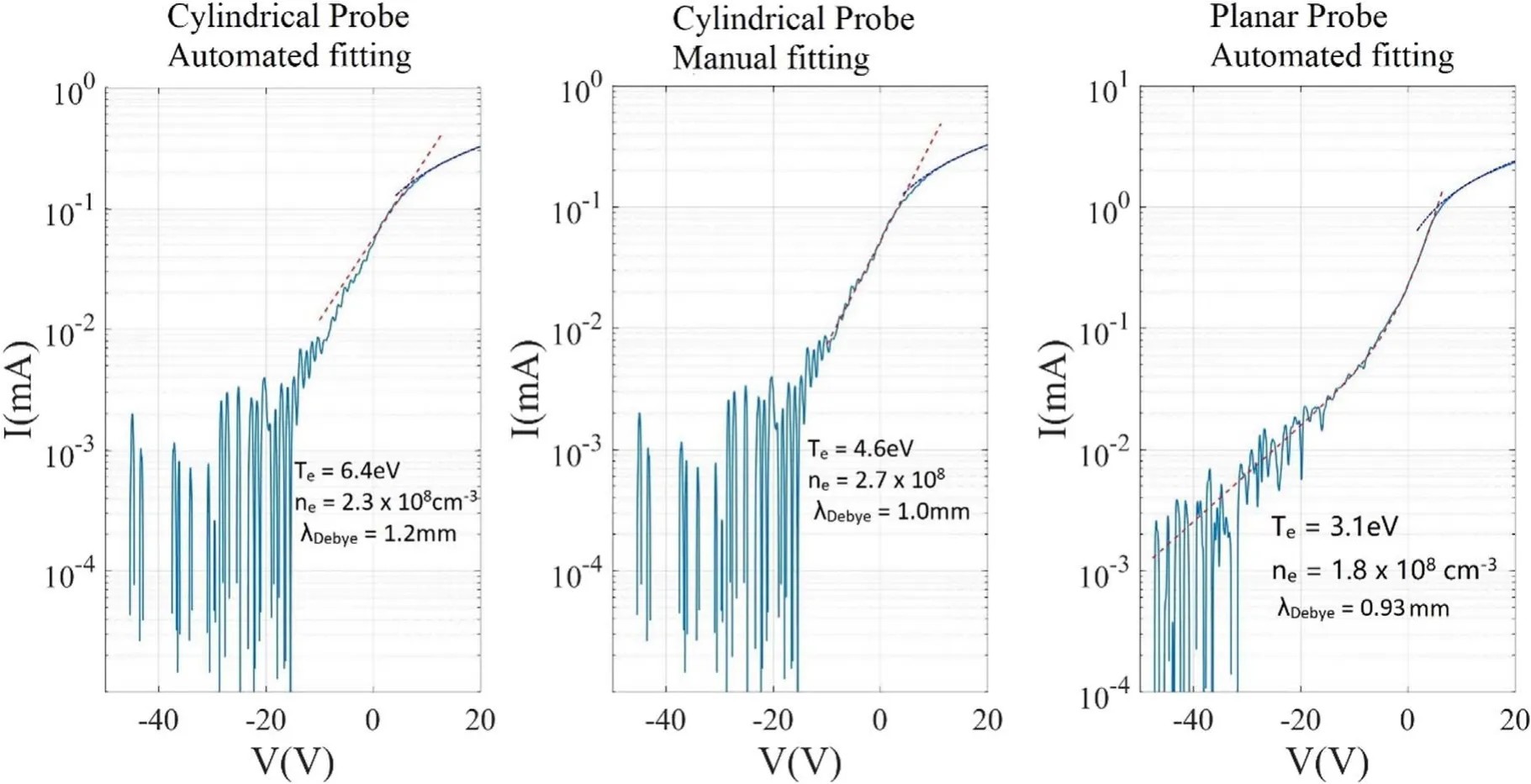
Figure 15.A 0.15 mm diameter cylindrical Langmuir probe trace in a 0.005 Pa, IDis = 0.2 A argon plasma analyzed through automatically and manually selecting Vinf. Also included is an automatically analyzed planar probe trace in a discharge with similar neutral pressure and discharge current.

By far the most comprehensive method to analyze a Langmuir probeI-Vtrace is to directly obtain the measured EEDF through the Druyvesteyn method[11].However,this method requires very good signal-to-noise ratio that might not be available. In these situations, conventional fitting of theI-Vtrace forTeandneis much more practical method as noise amplifications through the associated differential operations are avoided. It should also be noted that even EEDFs extracted through the Druyvesteyn method often need to be fitted forTeon semi-log graphs in order to be physically understood. In either case, fitting theI-Vtrace reconstructs the measured data through a combination of known distribution forms (in the case of this work, Maxwellian distributions)and finds the parameters that best reproduce theI-Vtrace.For parameters to be accurately extracted,a suitable fitting range must be decided. This is particularly important with multiple Maxwellian fitting in which the fitting range must both satisfy a reasonable signal-to-noise ratio and avoid the portion of theI-Vtrace where contributions of multiple electron populations overlap significantly.This is the primary reason why, if needed, multiple Maxwellian fittings have often been fitted manually in previous studies [10, 16].However, for experiments that have very large amount of data, fittingI-Vtraces manually is unrealistic. In this work,we present an iterative algorithm to automatically choose the fitting range for each electron temperature population,so that the position and size of the fitting range traces the temperature of the corresponding electron population, providing physically valid fitting ranges.The algorithm also fits theI-Vtrace for the plasma potential, provided that the EEDF is not drifting. The algorithm also defines criteria for which anI-Vtrace is not suitable for double or triple Maxwellian fitting and returns results of the lower order fittings if such criteria are satisfied.This is also important because,as experimental data show, not all EEDFs in all plasma sources under different working conditions can be properly described by single,double or triple Maxwellian distributions.These criteria act as fail-safe measures to prevent the automated procedures returning unphysical results under these circumstances.

It is also found that for probes behaving physically cylindrically as the Debye length increases with decreasing plasma density,poor signal-to-noise ratio significantly affects the determination ofVinf. This is because cylindrical sheath expansion results in higher dI/dVbeyondVp. This in turn affects the determination ofVinfand the fitting range forTe,as well as the plasma potential.In these cases,planar probes are recommended due to their pronounced transition to saturation resulting in a clearVinf.

Acknowledgments

This work is supported by the Chinese Academy of Science Hundred Youth Talent Program Start-up Funding, CAS Key Research Program of Frontier Sciences (No. QYZDB-SSWSLH001), National Natural Science Foundation of China(Nos. 11875285, 11575248 and 11505220), as well as US National Science Foundation Award (No. 1804654).