待定系數(shù)法解決一類三角函數(shù)的最值問題
廣東省中山紀(jì)念中學(xué)(528454) 鄧啟龍
高考真題(2018年高考全國(guó)卷Ⅰ理科第16 題)已知函數(shù)f(x)=2 sinx+sin 2x,則f(x)的最小值是____.
分析函數(shù)f(x)中既有sinx,又有sin 2x=2 sinxcosx,初看感覺無從下手,只能通過求導(dǎo)來求最值,于是得到解法一.然后觀察f(x)的結(jié)構(gòu),發(fā)現(xiàn)可以利用不等式來求最值,于是得到解法二,三,四.
解法一只需考慮一個(gè)周期[0,2π].

令f′(x)=0 得易得當(dāng)時(shí),f(x)取最大值,當(dāng)x=時(shí),f(x)取最小值
解法二先求f(x)在一個(gè)周期[0,2π]上的最大值.令則f(π ?x)=2 sinx ?sin 2x≤f(x),f(π+x)=sin 2x?2 sinx≤f(x),f(2π?x)=?2 sinx?sin 2x≤f(x),所以f(x)的最大值在上取到.易知sinx在[0,π]上凸,由琴生不等式得

解法三同解法二得f(x)的最大值在上取到.

當(dāng)且僅當(dāng)3(1?cosx)=1+cosx,即時(shí),f(x)取最大值又因?yàn)閒(x)是奇函數(shù),所以當(dāng)時(shí),f(x)取最小值
解法四f(x)=2 sinxcosx+2 sinx.假設(shè)當(dāng)sinx=a,cosx=b時(shí),f(x)取最大值,引入?yún)?shù)a,b >0,且a2 +b2=1.由得由sinx·a≤得于是

于是2 sinxcosx+2 sinx≤所以f(x)的最大值為當(dāng)且僅當(dāng)sinx=+2kπ(k∈?)時(shí),f(x)取最大值.又因?yàn)閒(x)是奇函數(shù),所以當(dāng)時(shí),f(x)取最小值
解法二把f(x)的表達(dá)式轉(zhuǎn)化為三個(gè)角的正弦,且這三個(gè)角的和是定值,然后利用琴生不等式求出函數(shù)最大值.解法三把f(x)的表達(dá)式轉(zhuǎn)化為正弦與余弦的乘積,然后利用多元均值不等式求出函數(shù)最大值,技巧性很強(qiáng).解法四利用待定系數(shù)法,通過假設(shè)f(x)取最大值時(shí)sinx,cosx的取值引入?yún)?shù),并利用結(jié)構(gòu)特點(diǎn)和取等條件構(gòu)造不等式,最后由系數(shù)的比例關(guān)系和參數(shù)滿足的條件求出參數(shù),進(jìn)而求出函數(shù)最大值.
變式探究若函數(shù)f(x)中既有sinx,sin 2x,又有cosx,cos 2x,即f(x)=psin 2x+qcos 2x+rsinx+scosx,p,r,s≥0,如何求函數(shù)f(x)的最大值? 此時(shí)解法一仍然適用,但是方程f′(x)=0 不好解.由于系數(shù)p,q,r,s的一般性,解法二和解法三就不適用了.本文通過探究發(fā)現(xiàn),解法四的待定系數(shù)法仍然可以解決這一類三角函數(shù)的最值問題.
假設(shè)當(dāng)sinx=a,cosx=b時(shí),f(x)=psin 2x+qcos 2x+rsinx+scosx取最大值,引入?yún)?shù)a,b >0,且a2+b2=1.由得由得由cosx · b≤得又qcos 2x=qcos2x ?qsin2x,于是

下面通過例題來說明如何利用待定系數(shù)法解決這一類三角函數(shù)的最值問題.
例1(第六屆世界數(shù)學(xué)團(tuán)體錦標(biāo)賽青年組試題第5 題)求函數(shù)f(x)=的最大值.
解f(x)=假設(shè)當(dāng)sinx=a,cosx=b時(shí),f(x)取最大值,引入?yún)?shù)a,b >0,且a2+b2=1.由得由sinx·a≤得由cosx·b≤得于是
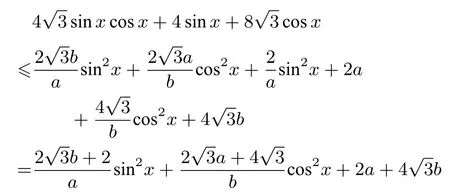
例2(《數(shù)學(xué)通訊》2018年第12 期問題376)求函數(shù)y=sinxcosx+3 sin(x+)+sin(x ?)的最大值.
解y=+ 3 sin(x+)+ sin(x ?).令得y=+ 3 sin(t+)+ sint=假設(shè)當(dāng)sint=a,cost=b時(shí),y取最大值,引入?yún)?shù)a,b >0,且a2+b2=1.由sint · a≤得由cost · b≤得于是

注如果把展開,將函數(shù)整理為psin 2x+rsinx+scosx的形式,系數(shù)很復(fù)雜,最后得到的方程很難解.本文先作代換然后將函數(shù)整理為qcos 2t+rsint+scost的形式,系數(shù)簡(jiǎn)單,最后得到的方程也好解.

