Jing Zhang,Fengying Wei,2?

(1.College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China;2.Key Laboratory of Operations Research and Control of Universities in Fujian,Fuzhou University,Fuzhou 350116,Fujian,PR China)

Abstract

Keywords stochastic SEIR model;media coverage;temporary immunity;persistence;extinction;stationary distribution

1 Introduction

It is necessary and important to reveal the transmission mechanisms of the infectious diseases incorporating media coverage and temporary immunity when human life is threatened in modern society.When the infectious diseases attack healthy population,the total population usually is separated into three compartments:the susceptible(S),the infected(I),the recovered(R)as referenced in some epidemic models,in which the corresponding dynamical patterns were proposed and investigated well.For instance,the epidemic models with vaccination[1,2],media coverage[1,3-8],temporary immunity[9-11],nonlinear incidence rate[5,10-12]have been considered in recent years.

Media coverage is one of the effective ways to control the spread of infectious diseases when infectious disease starts to invade the local population in a region[13,14].Usually,media coverage in modern societies,including television and radio,network and APPs,have been adopted to awake the awareness of people and to slow down the spread of infectious diseases.For COVID-19 epidemic course,local people obtain the information regarding the spread of infectious diseases via media terminal devices to avoid visiting high risk spot.Wearing masks when outing,washing hands when appropriate,these strategies what people obeyed are much helpful for the public health.As a consequence,the impacts of media coverage for slowing down the spread of infectious diseases are active and effective,which could be checked in the literature[1,3-8].

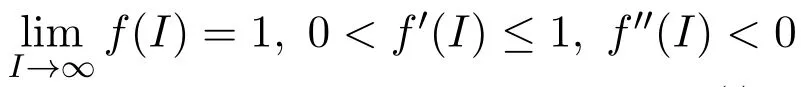
Another effective way to stop the spread of the infectious diseases is the vaccine.Immune system for each individual works well when vaccinated until losing the vaccine.In most articles[1,2,19-21],the valid period of vaccination was denoted by τ1,and the length of temporary immunity period was τ2.Recent studies[2,9,22,23]investigated the epidemic models with vaccination term S(t?τ1)e?μτ1,in which the individuals kept being susceptible after vaccinating for a specific time τ1.On the other hand,temporary immunity was built after a specific period of time τ2and the efficacy of the vaccine was less than one therewith being mentioned in the form of I(t? τ2)e?μτ2in[9,19,21-26].It means that the individuals lost their temporary immunities and return into the susceptible again.Recent related topics could be found in[18,27-31].

Motivated by the previous work,we propose an epidemic model incorporating vaccination and media coverage in this paper.We assume that epidemic model consists of four states:the susceptible(S),the exposed(E),the infected(I),the recovered(R),and Logistic type growth rS(1?)entered into the equation of the susceptible as a new recruitment term,where r is the intrinsic growth rate,and K is the maximum carrying capacity of the susceptible.

Based on the previous research regarding stochastic epidemic models[2,9,11,12,22-25,32-34],we aim at investigating a delayed stochastic epidemic model with media coverage and temporary immunity as follows:

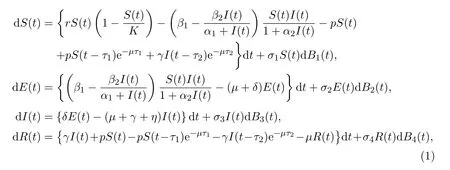
where S(t),E(t),I(t),R(t)indicate the population densities of the susceptible,the exposed,the infected,and the recovered individuals at time t respectively,μis the natural death rate of the total population,δ is the active infection rate of the exposed who turns into the infected,γ describes the recovery rate of the infected,η means the death rate due to disease,p denotes the vaccination rate within the susceptible.The term S(t? τ1)e?μτ1is the susceptible who are vaccinated at time t?τ1and keep bing susceptible at time t,and the term I(t?τ2)e?μτ2is the infected who are vaccinated t? τ2successfully,and lost the temporary immunity at time t to become the susceptible again.Parameters α1and α2are the half-saturation constants. σi＞ 0 denotes the intensity of the white noises,Bi(t)are standard independent Brownian motions which are defined on a complete probability space(?,F,{Ft}t≥0,P)with a filtration{Ft}t≥0satisfying the usual condition(that is,it is right continuous and F0contains all P-null sets)for i=1,2,3,4.

The arrangement of this article is as follows.In Section 2,we prove that model(1)admits a global positive solution with any positive initial value.In Section 3,by constructing suitable Lyapunov functions,the sufficient conditions for the persistence in the mean of positive solution of model(1)are established.In Section 4,we establish the sufficient conditions for the existence of stationary distribution,which is unique and ergodic.In Section 5,we derive the condition for the extinction of the disease.Consequently,some examples and numerical simulations are demonstrated to present our theoretical results of this paper.

2 Existence and Uniqueness of Positive Solution

3 Persistence in the Mean

For convenience,we define

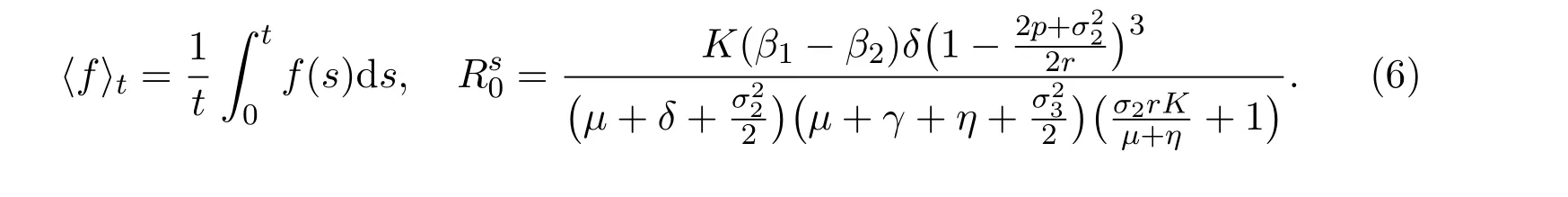
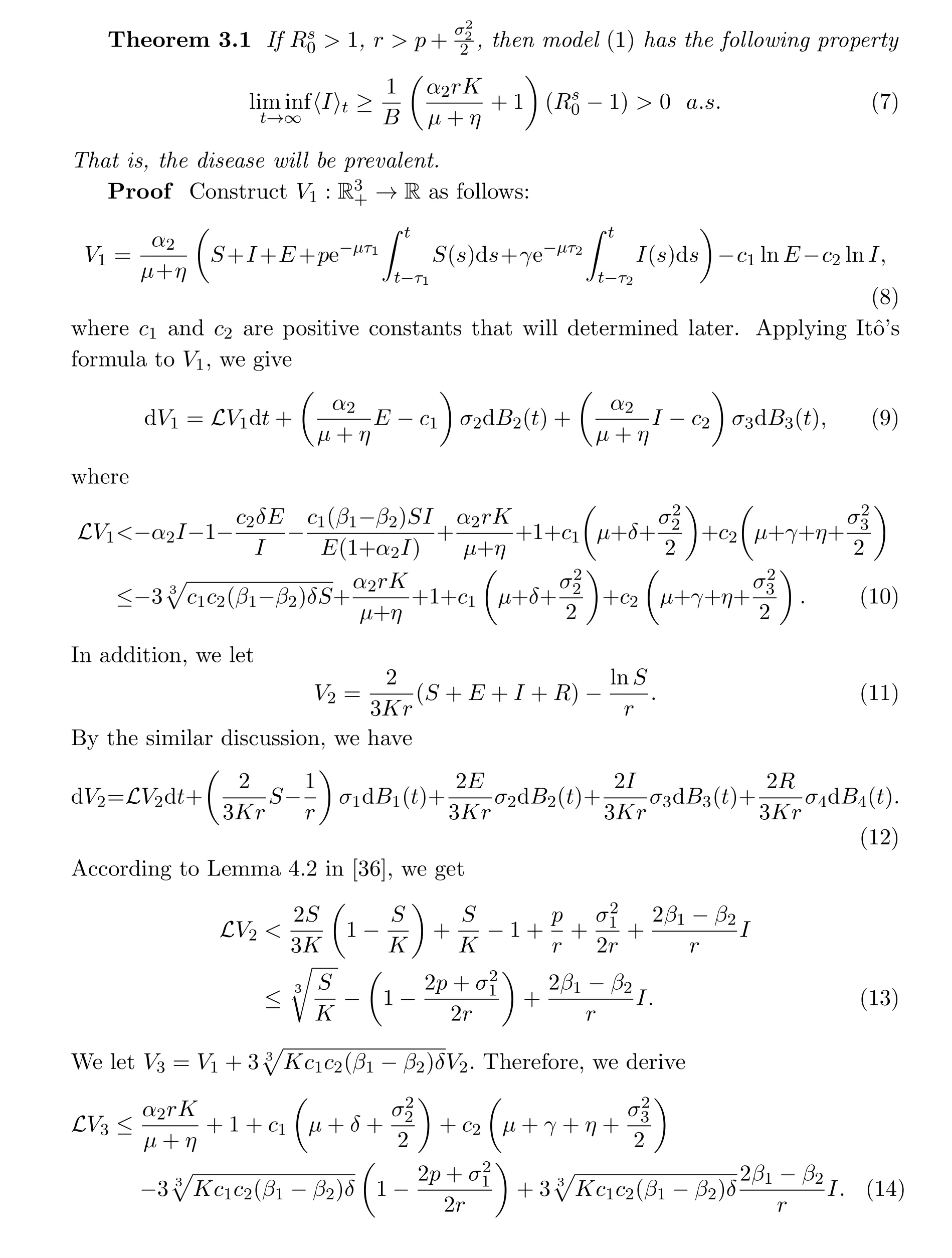
4 The Stationary Distribution

5 Extinction of the Diseases

In this section,we aim at investigating the sufficient conditions for the extinction of the disease.

Theorem 5.1 Let Z(t)be any solution of model(1)with initial value Z(0)∈R4+.If

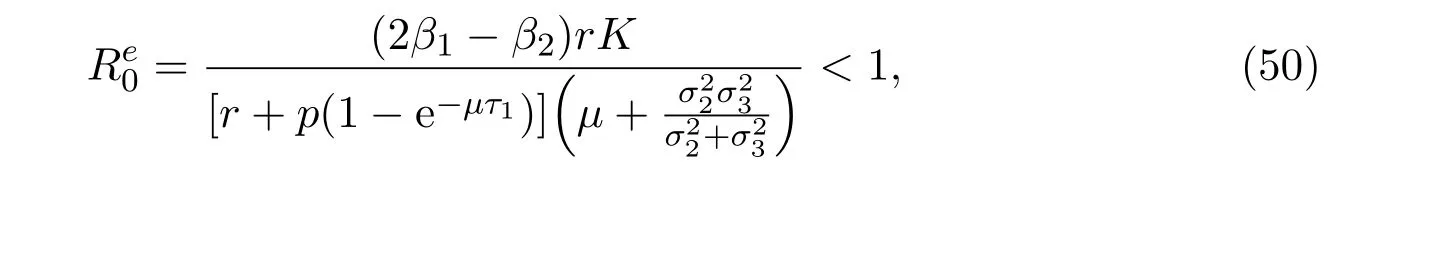
6 Examples and Simulations

By means of Milstein method in[39],several examples and corresponding numerical simulations will be presented to support the main results of this paper.

Example 6.1 We assume that the initial value is Z(0)=(0.5,0.3,0.2,0.2),and the parameters of model(1)are σ1=0.01,σ2=0.08,σ3=0.08,σ4=0.01,K=1.25,r=0.25,β1=0.5[3],β2=0.018[5],α1=0.1[3],α2=0.6[23],p=0.014[9],τ1=1[38],τ2=1[23],γ =0.06,μ =0.035,δ=0.15,η =0.03.A careful computation gives that

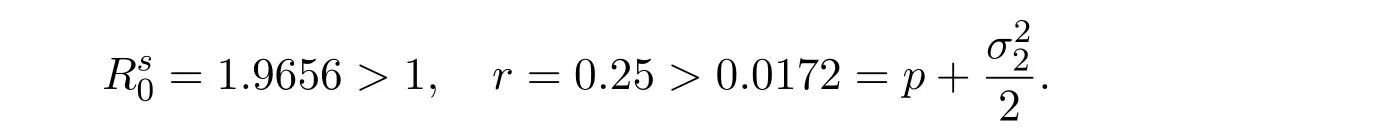
By Theorem 3.1,the solution of model(1)is persistent in the mean,which is shown in Figure 1.

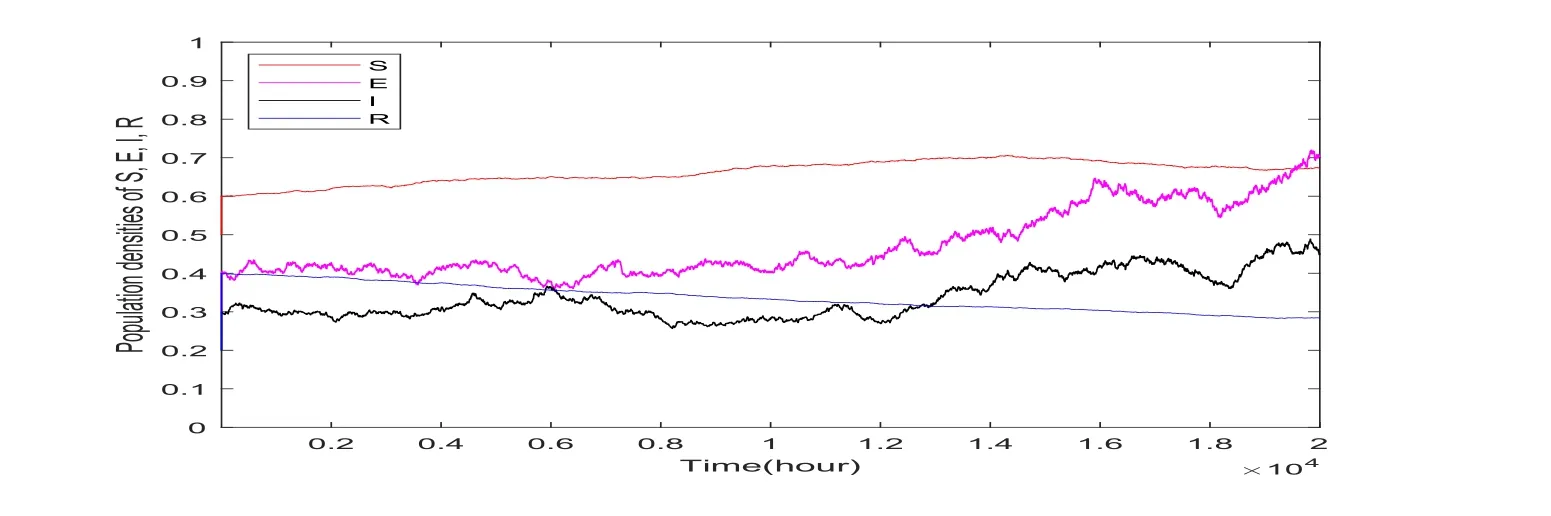
Figure 1:A realization of the solution of model(2),which is persistent in the mean.

Example 6.2 We assume that the initial value is Z(0)=(0.9,0.7,0.5,0.6),and the parameters of model(1)are σ1=0.01,σ2=0.08,σ3=0.08,σ4=0.01,K=1.25,r=0.35,β1=0.5,β2=0.018,α1=0.1,α2=0.6,p=0.014,τ1=1,τ2=1,γ =0.06,μ =0.035,δ=0.15,η=0.03.A careful computation gives that

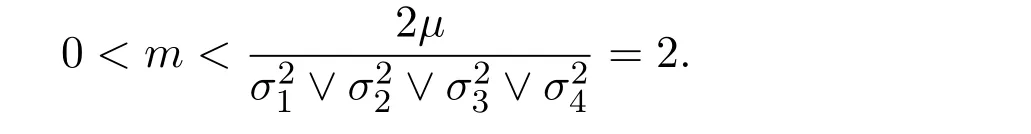
By Theorem 4.1,model(1)admits a unique stationary distribution as shown in Figure 2.

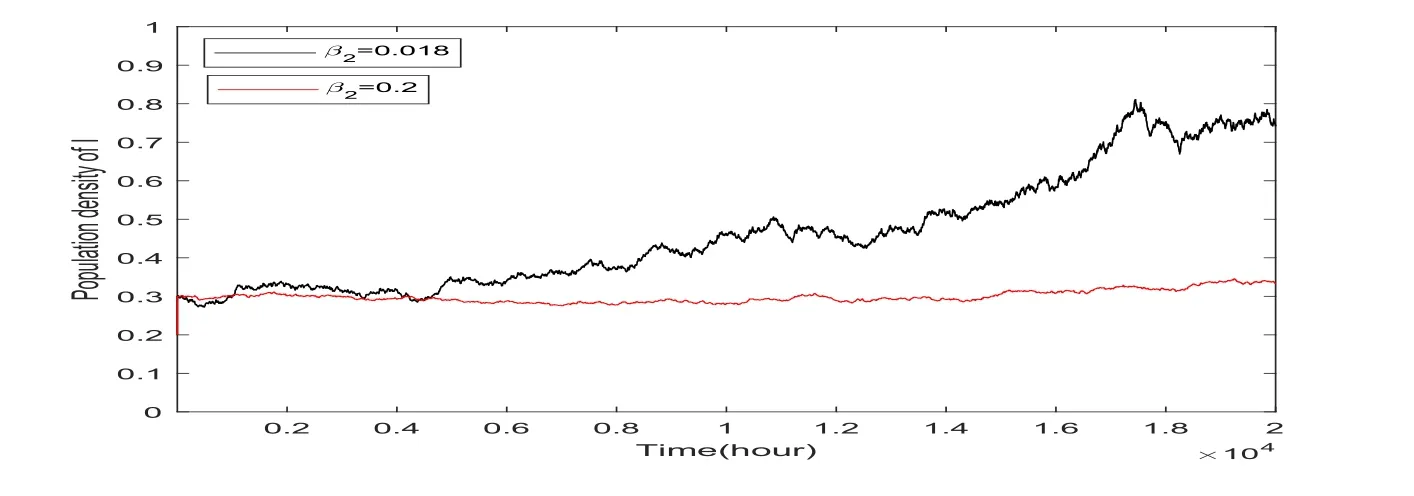
Figure 2:Population density of the infected declines when β2increases.

Example 6.3 We set the initial value to be Z(0)=(0.3,0.2,0.2,0.2)and parameters of model(1)are σ1=0.01,σ2=0.08,σ3=0.08,σ4=0.1,K=1.25,r=0.2,β1=0.78[5],β2=0.18[5],α1=0.1[23],α2=0.6[23],p=0.48[9],τ1=1,τ2=1,γ =0.5,μ =0.1,δ=0.15,η=0.13.Substituting them into the condition of Theorem 5.1,a careful computation gives that=0.1449＜1,then,the disease tends to extinction as presented in Figure 3.

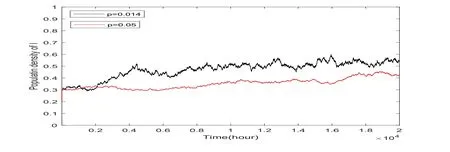
Figure 3:Population density of the infected declines when p increases.

7 Conclusion and Discussion

In this paper,the existence and uniqueness of the positive solution,extinction and persistence,and stationary distribution as well are investigated for a stochastic SEIR epidemic model with media coverage and temporary immunity.

First,we prove that,for any given initial value,model(1)admits a unique global positive solution.Further,under the conditionsthe persistence in the mean of the solution is checked in Theorem 3.1 and being presented in Figure 1.The numerical simulation for media effects of β2and vaccine rate p are considered finally.Precisely speaking,media reports have reduced the contact rate β.In other words,when β2increases,the tendency of prevalence to COVID-19 epidemic course will decrease as shown in Figure 2.We also find that,as a result of vaccination,more susceptible individuals obtain immunity when p increases,which will protect people against being infected by COVID-19 epidemic course.That is,when p increases,the tendency of the prevalence will slow down as shown in Figure 3.

Moreover,by constructing Lyapunov functions,the sufficient condition for the stationary distribution of a positive solution to model(1)is obtained in Theorem 4.1.The ergodicity of model(1)provides a biological perspective for understanding epidemic models with fluctuating environments,which could be found in Figure 4.

Finally,we prove that,under condition＜1,the disease tends to extinction in Theorem 5.1 as demonstrated in Figure 5.The numerical simulations present that when β2and p increase,the time for extinction of the infected individuals becomes earlier as shown in Figures 6 and 7.

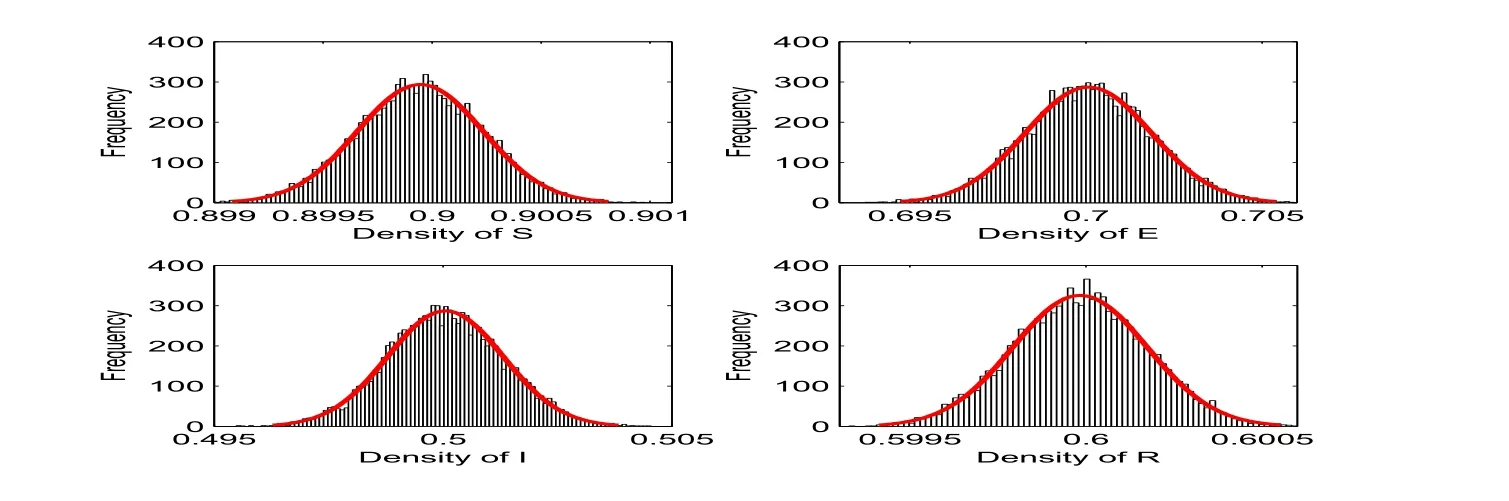
Figure 4:The histogram for susceptible-exposed-infected-recovered model(1).

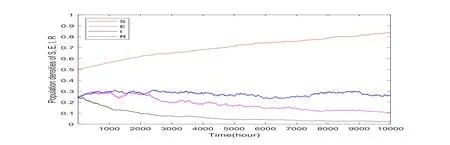
Figure 5:A realization of the solution to model(2),which is extinct when ＜1.

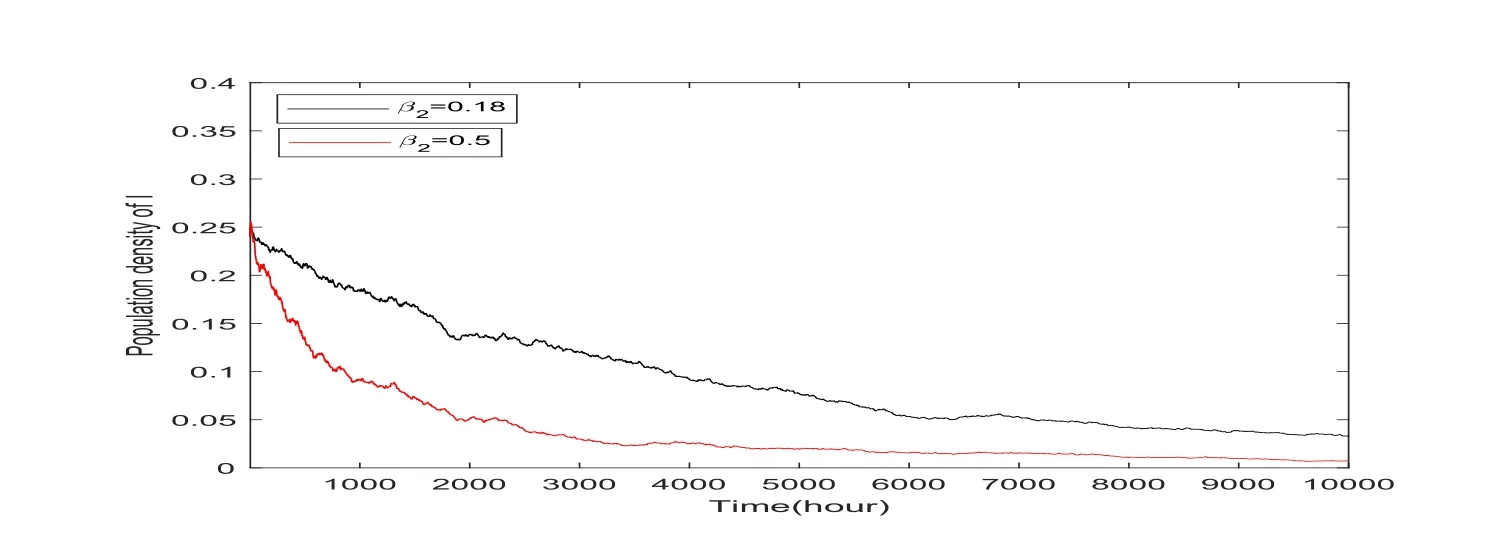
Figure 6:Population density of the infected declines when β2increases.

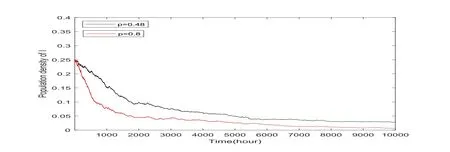
Figure 7:Population density of the infected declines when p increases.

Acknowledgement The authors are thankful to the editor and the referees for their valuable comments and suggestions for the improvement of this paper.