Novel structures and mechanical properties of Zr2N:Ab initio description under high pressures*
Minru Wen(文敏儒), Xing Xie(謝興), Zhixun Xie(謝植勛), Huafeng Dong(董華鋒),?, Xin Zhang(張欣),Fugen Wu(吳福根), and Chong-Yu Wang(王崇愚)
1School of Physics and Optoelectronic Engineering,Guangdong University of Technology,Guangzhou 510006,China
2School of Materials and Energy,Guangdong University of Technology,Guangzhou 510006,China
3Department of Physics,Tsinghua University,Beijing 100084,China
Keywords: phase transition,phonon dispersion,Zr2N,first-principles calculations
1. Introduction
As key materials for cutting coatings, super wearresistance, and thermal barrier coatings, group IVB transition metal nitrides (TMNs; TM=Ti, Zr, and Hf) have been widely used in mold-making industries,automobile manufacturing, and aerospace industries owing to their high melting point, excellent chemical stability, corrosion resistance, and metallic conductivity.[1–4]In the TMNs,the well-known stable phase is the stoichiometric B1-TMN compound with a rocksalt structure(space group Fmm). However,the TMNs may display a variety of compositions and phases featuring both cation and nitrogen enrichment.[5–8]Owing to the improvement of high-temperature and high-pressure experimental conditions, novel TMNs such as Th3P4-Zr3N4[9]and I4/mcm-TiN2[10]have been experimentally synthesized and exhibit excellent mechanical properties. With metalloid vacancies displaying long- or short-range order, or both, most TMNs(TMNx,for x=0–1)exist on the metal-rich side(i.e.,x<0.5)of the phase diagram.[5–7]However, compared to transition metal (TM) sub-nitrides, more research has focused on stoichiometric TMNs and nitrogen-rich TMNs. Consequently,an investigation of novel stable crystal structures for metal-rich TMNs under high pressure is essential for the development of practical applications.
Numerous studies exist on the phase stability, electronic structure,and mechanical properties of Ti-N,[11–17]Zr-N,[11–16,18–20]and Hf-N[12–16,18,21]systems. Recent studies using the evolutionary algorithm/search algorithm and density functional theory(DFT)have investigated the stable structures and possible stoichiometries of the TMN[15–17,20,21]systems. Yu et al.[17]explored the stable structures and possible stoichiometries of the Ti-N system at the pressures of 0 GPa, 20 GPa, and 60 GPa and found the new ground structures Ti3N2, Ti4N3, and Ti6N5at atmospheric pressure and two novel stable phases Cmcm-Ti2N and I4/mcm-TiN2at high pressures (synthesized by Bhadram et al. using the laser-heated diamond anvil cell technique at 73 GPa and 2400 K[10]).Weinberger et al.[15]investigated candidate stable structures of the group IVB and group VB TMNs at ambient pressure and demonstrated that the stable phase of Ti2N and Zr2N is the tetragonal P42/mnm phase, while Hf2N is more energetically favorable in the orthorhombic Pnnm phase. Research by Yu et al.[20]revealed that Fmm-ZrN, P42/mnm-Zr2N,C2/m-Zr4N3,C2/m-Zr6N5,C2/m-Zr8N7,P-Zr15N16,P-Zr7N8, and C2/m-Zr4N5are ground-state structures at 0 GPa and low temperatures. Zhang et al.[21]studied the pressure-composition phase diagram for the Hf-N system under 0–60 GPa and revealed new candidate phases with a Hf:N ratio of 6:1,3:1,and 3:2 at zero pressure.Zirconium as well as Ti and Hf are group IVB TMs whose nitrides display similar phase transitions,chemical bonding,and elasticity. Unlike many studies for titanium and hafnium nitrides, the investigations of novel structural phases of high-pressure zirconium nitrides are limited. Specifically, no theoretical study has yet focused on new crystal structures of Zr-rich nitrides under high pressures.
Considering this background, the present research focuses on novel crystal configurations of zirconium sub-nitride Zr2N at 0–200 GPa by combining evolutionary searches and first-principles calculations. By calculating the elastic constants and phonon spectra,the mechanical and dynamical stabilities for all candidate structures are evaluated. Additionally,the electronic and mechanical properties of the crystal phases are systematically analyzed to reveal the potential applications of the binary zirconium heminitrides.
2. Computational methods
To identify all potential novel Zr2N crystal structures,the evolutionary algorithm method implemented in the USPEX code[22–24]with variable cell number (up to 30 atoms)is performed at pressures of 0 GPa,30 GPa,60 GPa,90 GPa,120 GPa,150 GPa,and 200 GPa. We set the number of structures in the population to be 100,thus producing at random the first generation of structures. The 50 structures in the subsequent generations are produced by heredity(40%),soft mutation(20%),transmutation(20%),and randomness(20%).
The structural relaxations (i.e., optimization of lattice shape, volume, and atomic positions) and energies of every structure along with all calculations of the properties of interest are executed in the VASP code[25]based on DFT.[26,27]The projector augmented-wave method[28]is adopted for the ionelectron interactions,and the generalized gradient approximation of Perdew et al.[29]is used for the exchange-correlation function. Electrons in the 4s24p64d25s2and 2s22p3orbitals are considered as valence electrons for Zr and N, respectively. The plane-wave kinetic energy cutoff is set to 600 eV.Monkhorst-Pack[30]k-meshes with a resolution of 2π×0.04 ?A are adopted to characterize the energy integration in the Brillouin zone. The criteria for the force on the atoms are set at 0.01 eV/?A for ion self-consistency, while the energy convergence of the electronic self-consistency is set to be 10-5eV per atom.
Using a 2×2×2 supercell, the phonon dispersion relations are achieved in the framework of density functional perturbation theory[31,32]as implemented in the PHONOPY package[33]as well as the VASP code. The elastic constants are calculated by the strain–stress method,[34]and the elastic moduli (i.e., bulk modulus B, shear modulus G, and Young’s modulus E)as well as Poisson’s ratio ν,are obtained under the Voigt–Reuss–Hill approximation.[35–37]Employing Chen’s model,[38]the theoretical Vickers hardness values are estimated using
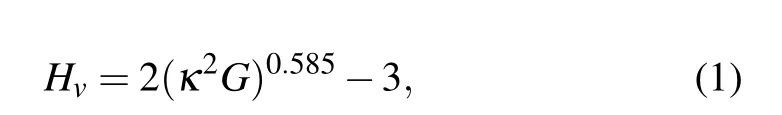
where κ =G/B is the Pugh ratio. The directional dependence of Young’s modulus is also calculated to reveal the anisotropy of all potential Zr2N phases.
3. Results and discussion

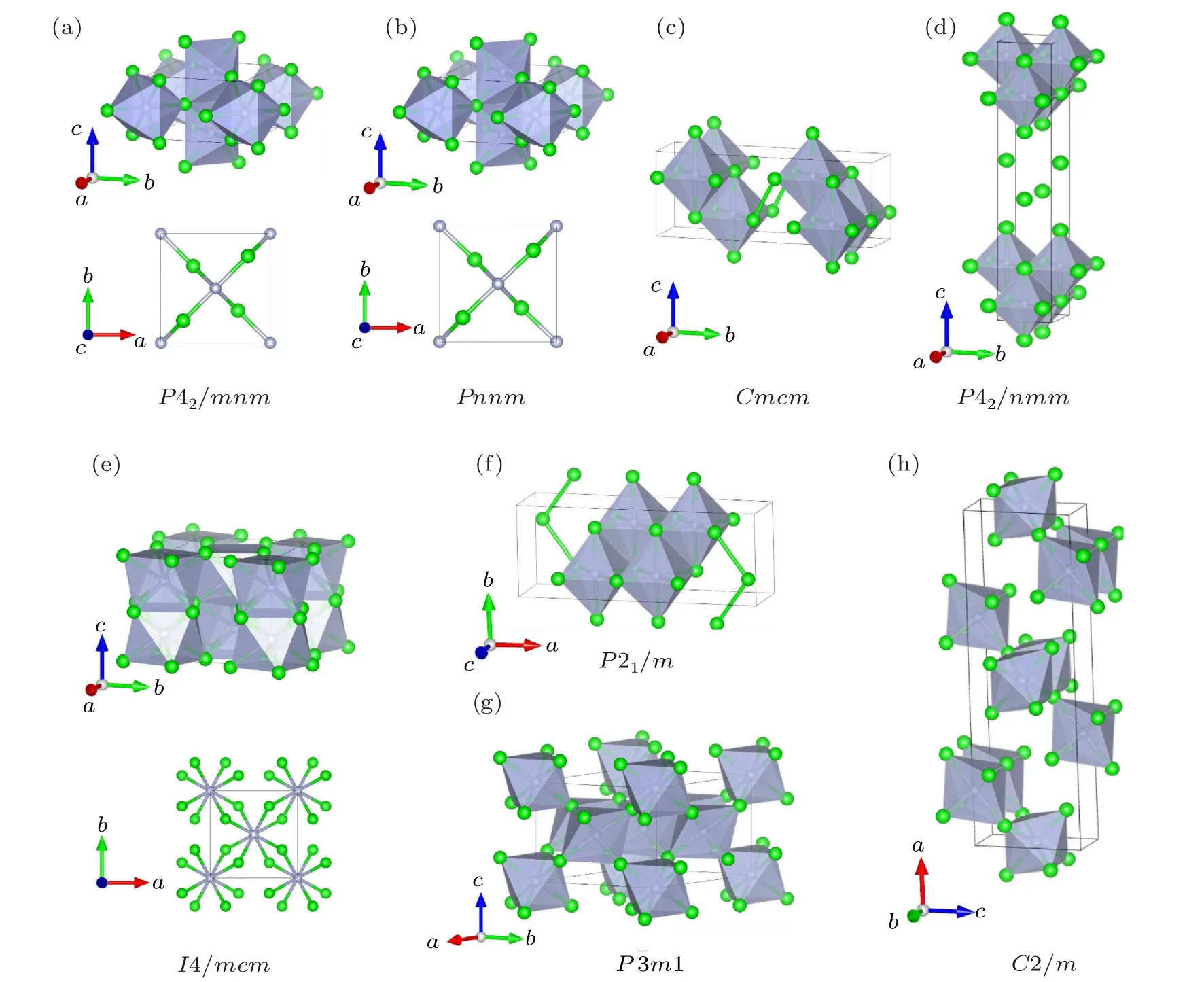
Fig. 1. Schematic crystal structures of potential Zr2N for (a) P42/mnm, (b) Pnnm, (c) Cmcm, (d) P4/nmm, (e) I4/mcm, (f) P21/m,(g)Pm1,and(h)C2/m phases at 0 GPa. The schematic shows the N atoms(gray circles)in the centers of the gray polyhedrals and the Zr atoms(green circles).
As displayed in Fig. 1, although the Cmcm, P4/nmm,and P21/m phases belong to different crystal systems and have different symmetries, they demonstrate similar characters wherein all N atoms are octahedrally coordinated by six Zr atoms and the NZr6octahedrons arrange along a uniform direction. In fact,the Cmcm,P4/nmm,and P21/m phases are versions of the rocksalt B1-TiN(space group Fmm,No.225)with ordered N-vacancies. Likewise,vacancy-ordered phases have also been reported for group IVB TMNs[17,21]and carbides.[39,40]In the Pm1 and C2/m phases, N atoms are also centered in the octahedron(composed of Zr atoms)interstices, though NZr6octahedrons arrange along different orientations. There are 12 atoms in a unit cell of the anti-rutile structure of the I4/mcm phase,of which the metal Zr and nonmetal N atoms occupy the Wyckoff 8h and 4a positions, respectively. Each N atom is coordinated by eight Zr atoms,forming a decahedron.This crystal structure naturally reminds us of the I4/mcm-TiN2phase belonging to the same space group,where the metal atoms and nitrogen atoms in I4/mcm-TiN2and I4/mcm-Zr2N phases occupy the opposite Wyckoff positions.However,unlike the short NN dumbbell bond length of I4/mcm-ZrN2,which is as short as 1.424 ?A at 1 atm,[16]the Zr–Zr bond length of I4/mcm-Zr2N is as long as 2.981 ?A at ambient pressure. It can therefore be predicted that the mechanical strength and hardness of I4/mcm-Zr2N will be significantly less than those of I4/mcm-ZrN2.
To ascertain the thermodynamic stability of the predicted Zr2N configurations, we obtain the formation enthalpies per atom ΔH using
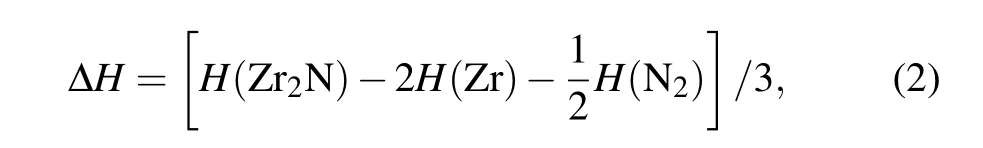
where H(Zr2N),H(Zr),and H(N2)are the enthalpies per formula unit of Zr2N, P63/mcm-Zr, and α-N2, respectively, at a specific pressure. Our determined formation enthalpies of all Zr2N candidate phases at 0 GPa are summarized in Table 1.It can be seen that P42/mnm-Zr2N is the most stable phase of zirconium heminitride at atmospheric pressure with the formation enthalpy calculated to be-1.2914 eV per atom,which agrees well with the result of-1.249 eV/atom from Ref. [21].As a distorted version of ε-Zr2N(see Figs.1(a)and 1(b)),we note that the ΔH of the Pnnm phase is only slightly higher than that of P42/mnm-Zr2N.As shown in Table 1,the I4/mcm phase exhibits the highest formation enthalpy among the eight phases, indicating that I4/mcm Zr2N is the least energetically favorable phase for zirconium heminitride at 0 GPa.
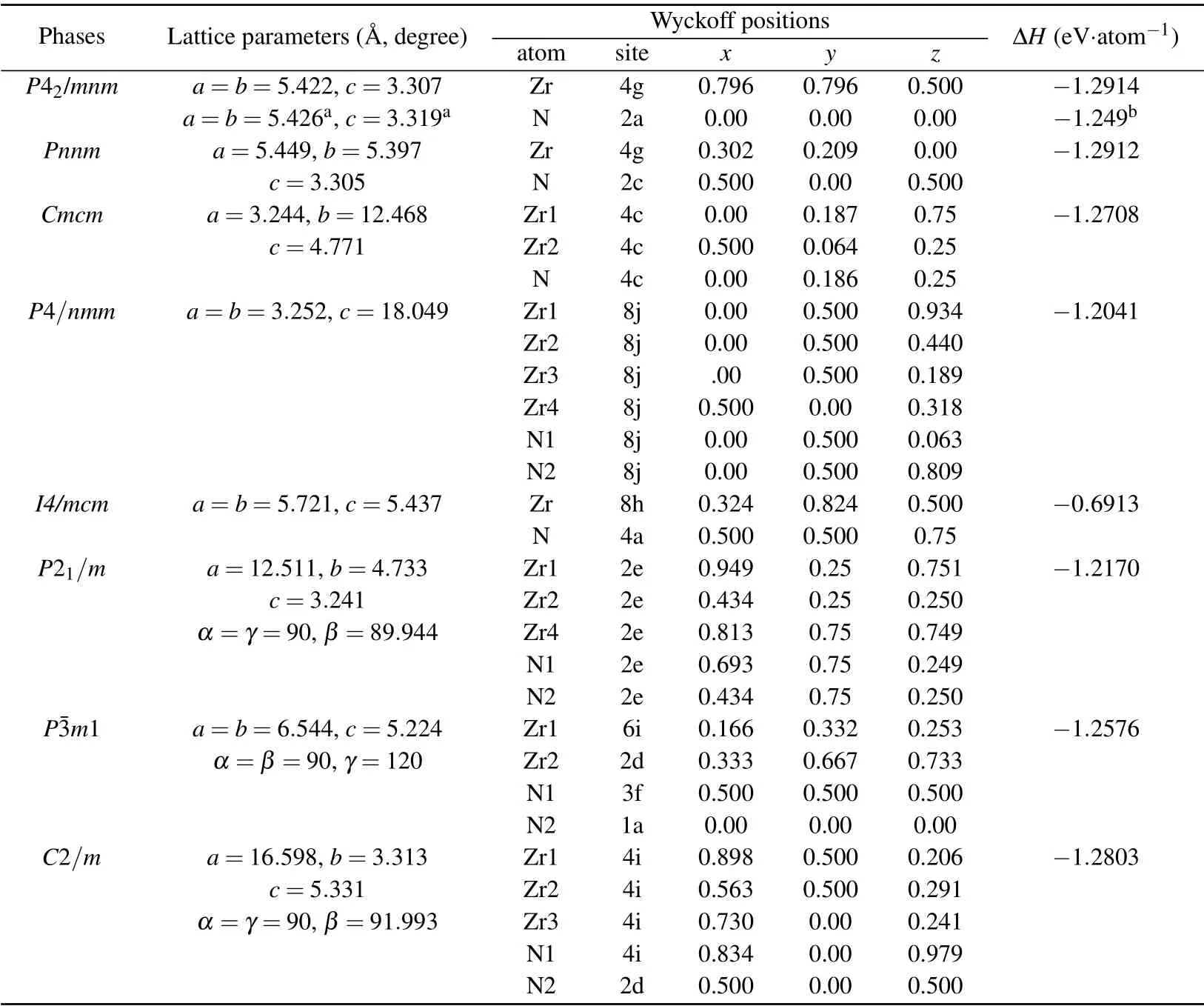
Table 1. Structural parameters(lattice constants and atomic coordinates)and formation enthalpies ΔH of the candidate phases of Zr2N at 0 GPa,along with other DFT-predicted values.
To further investigate the phase transition of Zr2N at high pressure, the enthalpies of these candidate configurations are calculated as a function of pressure up to 200 GPa. Figure 2 plots the calculated enthalpy(relative to the Cmcm phase)per atom as a function of pressure for all candidate phases and the inset shows a detail of the enthalpy-pressure curves for the 3–17 GPa pressure range. As demonstrated in Fig.2,the diverse crossings between different structures in the pressure range of 0–200 GPa indicate the existence of various structural phase transformations for Zr2N under pressure. The P42/mnm-Zr2N transforms to Pnnm-Zr2N at approximately 6.5 GPa, whereupon Pnnm-Zr2N transforms to Cmcm-Zr2N at 16.3 GPa.This is different from the scenario of Ti2N and Hf2N. Specifically,the stable crystal structure of titanium heminitride at the ambient pressure (i.e., P42/mnm-Ti2N) transforms directly to Cmcm-Ti2N at 20.8 GPa.[17]In terms of hafnium heminitride,the orthorhombic Pnnm-Hf2N phase,which is the most stable configuration at atmospheric pressure, transforms to Cmcm-Hf2N at 12.5 GPa.[21]According to Fig.2,though the Cmcm-Zr2N is initially the most energetically favorable when the pressure exceeds 16.3 GPa, other phases become more energetically favorable as the pressure increases further. For example,the P4/nmm-Zr2N phase exhibits a lower enthalpy than Cmcm-Zr2N at 55.2 GPa, as does the P21/m-Zr2N phase at 65.0 GPa, where the P4/nmm-Zr2N phase possesses the lowest enthalpy from 55.2 GPa to 144.4 GPa. When the pressure further increases, the P4/nmm and P21/m phases both transform to the I4/mcm configuration at pressures of 122.8 GPa and 144.4 GPa, respectively. This signifies that the I4/mcm-Zr2N phase is the most energetically-favored structure in the 144.4–200 GPa pressure range. The enthalpies of the Pm1 and C2/m phases are higher than those of the Pnnm phase during the entire studied pressure range,but these phases possess a lower enthalpy than the P42/mnm phase when the pressure exceeds 34.5 GPa and 40.3 GPa,respectively.
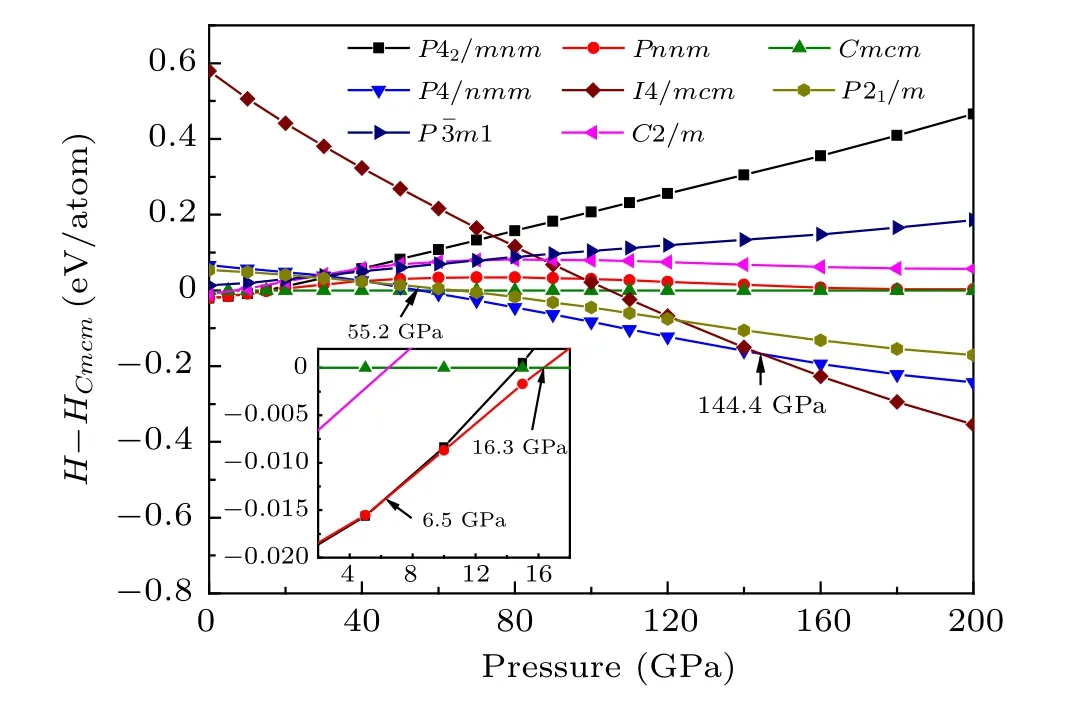
Fig. 2. Calculated enthalpy curves as a function of pressure for the different phases of Zr2N,with reference to the Cmcm phase. Inset: Detail of the enthalpy–pressure curves in the 3–17 GPa pressure range.
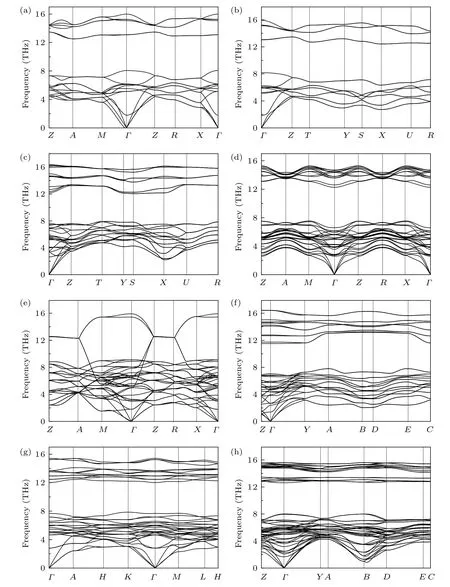
Fig. 3. Phonon dispersion curves for (a) P42/mnm, (b) Pnnm, (c) Cmcm, (d) P4/nmm, (e) I4/mcm, (f) P21/m, (g) Pm1, and (h)C2/m phases at 0 GPa,respectively.
Next,the dynamical and mechanical stabilities of the candidate Zr2N structures are investigated using the phonon spectra and elastic constants.The calculated phonon frequencies of the five novel structures(P4/nmm,I4/mcm,P21/m,Pm1,and C2/m)and the P42/mnm,Pnnm,and Cmcm phases of Zr2N at atmospheric pressure are plotted in Fig. 3. Clearly, there are no imaginary frequencies for all predicted phases at 0 GPa,signifying that these configurations are all dynamically stable.The calculated phonon dispersion curves of P42/mnm-Zr2N in this study are consistent with previous DFT results.[20]In addition to ambient pressure,we also study the phonon stability of all structures under high pressure. Soft phonons are found in ε-Zr2N,P4/nmm-Zr2N,and C2/m-Zr2N with an initial negative slope at the Γ point(related to crystal instability under a homogeneous deformation)for pressures of 20 GPa,200 GPa,and 120 GPa,respectively. This suggests the existence of mechanical instability in ε-Zr2N,P4/nmm-Zr2N,and C2/m-Zr2N at these corresponding pressures.[41]The Cmcm,I4/mcm,and P21/m phases,however,maintain their phonon stability above 200 GPa, while the Pnnm and Pm1 configurations hold dynamic stability up to 200 GPa and 160 GPa,respectively.
The elastic constants were obtained using the strainstress method and are summarized in Table 2. The P42/mnm,P4/nmm,and I4/mcm structures belong to the tetragonal crystal system (Laue class of 4/mmm) and have six independent elastic constants. The mechanical stability criteria of the tetragonal crystal are given as[42–44]
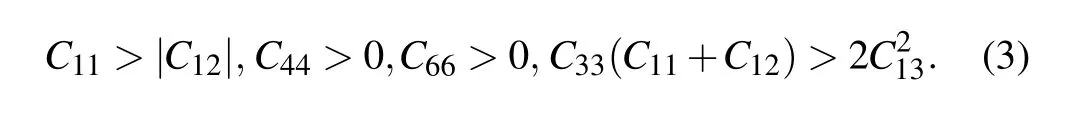
The Pnnm- and Cmcm-Zr2N are both orthorhombic crystal systems with nine independent elastic constants. The mechanical stability criteria for an orthorhombic class are[45]
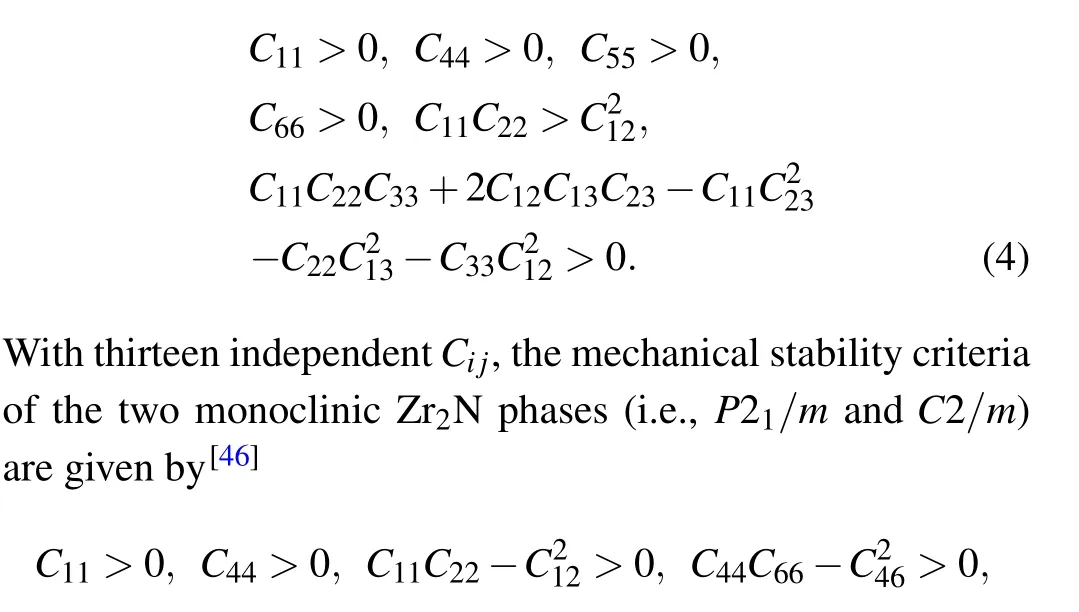

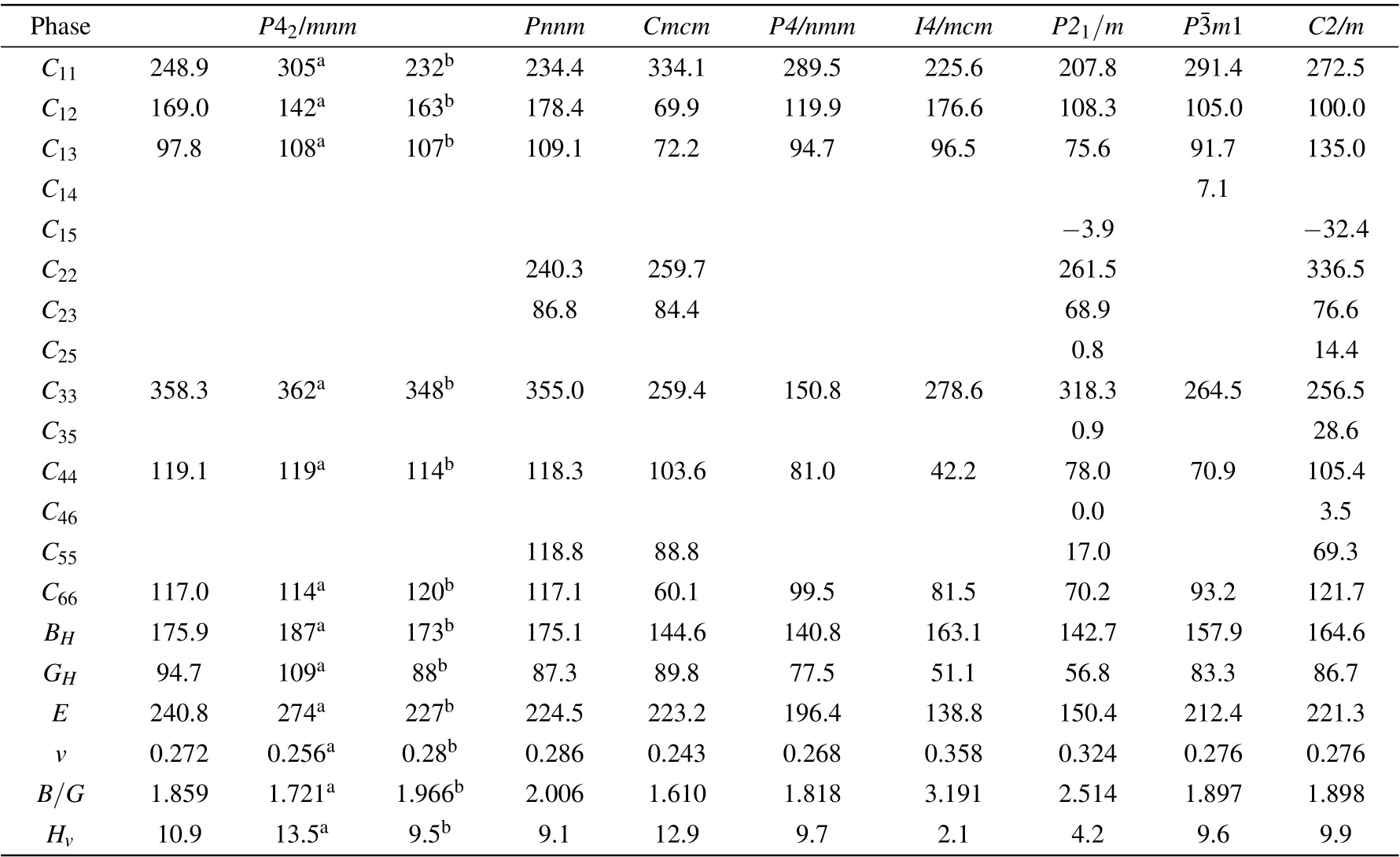
Table 2. Calculated elastic constants(Cij),elastic moduli(i.e.,bulk modulus BH,shear modulus GH,and Young’s modulus E),B/G ratio,Poisson’s ratio(v),and Vickers hardness(Hv)of the Zr2N compounds at zero pressure,along with other DFT calculated values. Ci j,BH,GH,E,and Hv are in GPa,B/G,and v are dimensionless.
The constants C11,C22, and C33reflect the resistance of the crystal to normal strain in the[100],[010],and[001]directions,respectively. As mentioned above,the Cmcm,P4/nmm,and P21/m phases are versions of the cubic B1-TiN possessing ordered nitrogen vacancies.As shown in Table 2,P21/m-Zr2N possesses the lowest C11among the eight predicted structures.This is because the N-vacancies of the P21/m phase are distributed in the(100)plane and the least-dense atomic arrangement is in the [100] direction (see Fig. 1). Similarly, the Nvacancies of the P4/nmm phase are distributed in the (001)plane and the atomic compactness in the[001]direction is the worst (shown in Fig. 1). The P4/nmm-Zr2N phase possesses the lowest C33value among the eight candidate structures.Conversely, the Cmcm,C2/m, and P42/mnm phases respectively exhibit the highestC11,C22,andC33values.We note that our calculated elastic constants(except C11)of P42/mnm-Zr2N are consistent with the results of Yu et al.,[20]and our calculated C11of ε-Zr2N agrees well with the result of Ref. [48].
The elastic moduli (i.e., bulk modulus BH, shear modulus GH,and Young’s modulus E),B/G ratio,Poisson’s ratio v,and Vickers hardness Hvof the Zr2N compounds at zero pressure are further studied by the methods mentioned in Secion 2 and are summarized in Table 2. Clearly, ε-Zr2N exhibits the largest bulk,shear,and Young’s moduli among the Zr2N compounds, which indicates that ε-Zr2N has the best resistance to volume change and shear shape deformation, and the best stiffness. Notably, the Pnnm phase, which is a distorted version of the ε-Zr2N phase,has similar but lower elastic moduli compared with those of the ε phase. The P4/nmm-Zr2N phase exhibits the smallest BHvalue,while I4/mcm-Zr2N possesses the smallest GHand E values.
The B/G ratios (proposed by Pugh[49]) of all structures except the Cmcm phase are larger than 1.75, implying that the P42/mnm, Pnnm, P4/nmm, I4/mcm, P21/m, Pm1, and
C2/m phases belong to ductile materials, where the I4/mcm phase is the most ductile among these configurations. In contrast,Cmcm-Zr2N possesses the smallest B/G ratio and Poisson’s ratio v,which is the most brittle phase among the Zr2N compounds.Intriguingly,owing to its brittleness,Cmcm-Zr2N exhibits the highest Vickers hardness (12.9 GPa), though its shear modulus is lower than that of ε-Zr2N. Contrarily, the I4/mcm phase has the lowest hardness as small as 2.1 GPa at ambient pressure. Note here that the I4/mcm phase has the lowest shear modulus,Young’s modulus,and hardness among the studied structures,where its abnormal and relatively higher bulk modulus primarily originates from its large mass density.
Moreover, we investigate the directional dependence of Young’s modulus for all predicted Zr2N phases (see Fig. 4).Although the eight candidate configurations possess identical chemical composition ratios, their mechanical properties exhibit considerable differences. Young’s modulus of the Pm1 phase displays the most isotropic features among the Zr2N compounds because its three-dimensional Young’s modulus diagram shape is the closest to a sphere. Looking at the diagram shapes in Fig.4 and the degree of their deviation from spherical,the P21/m-Zr2N phase exhibits the most anisotropic features, followed by the Pnnm and I4/mcm phases. The anisotropy of the P21/m-Zr2N arises from the high C33and C22values and the low C23value,resulting in a large Young’s modulus in the y- and z-axis directions and a small E in the diagonal directions of the y–z plane. The anisotropy of the Pnnm and I4/mcm phases is mainly owing to their relatively low C11and C22values and high C12value,resulting in a small Young’s modulus in the x-and y-axis directions and a large E in the diagonal directions of the x–y plane.
To understand the electronic properties and bonding features of these zirconium heminitrides, we further study the density of states (DOS) of each system. Figure 5 shows the s- and p-orbital partial DOS of N, the d-orbital partial DOS of Zr, and the total DOS for all Zr2N phases. Notably, all Zr2N compounds are metallic owing to the finite DOS at the Fermi level,which are dominated by the 4d orbitals of the zirconium atoms (see Fig. 5). Owing to the contribution of the 2s orbitals of the N atoms, all studied configurations exhibit a deep valence band below -12 eV. Similar to the scenario reported in the Tin+1Nn(n=1,2,3,and 5)structures,[17]interactions exist here between Zr and N atoms. According to Fig. 5, these interactions originate from the hybridization of the N-2p states and Zr-4d states in the energy region of-7 eV to -2.5 eV. We note that the interaction between Zr and N in the Cmcm phases exhibits greater hybridization than that in the P4/nmm and P21/m structures. This suggests that Cmcm-Zr2N will possess better mechanical strength and deformation resistance than the P4/nmm and P21/m phases, which is consistent with the calculated results of the elastic moduli in Table 2. Unlike the strong covalent N–N bonding nature in the I4/mcm-type TM pernitrides, weaker interactions are exhibited by the covalent-like Zr–N bond and metallic Zr–Zr bond in the I4/mcm-Zr2N phase. Consequently,compared with I4/mcm-type TM pernitrides,the I4/mcm-type TM heminitrides possess reduced mechanical strength and hardness.For example,compared with the values exhibited by I4/mcm-Zr2N, the I4/mcm-ZrN2structure exhibits larger calculated bulk modulus (1.7×), shear modulus (3.4×), Young’s modulus(3.1×),and hardness(12.3×).[16]
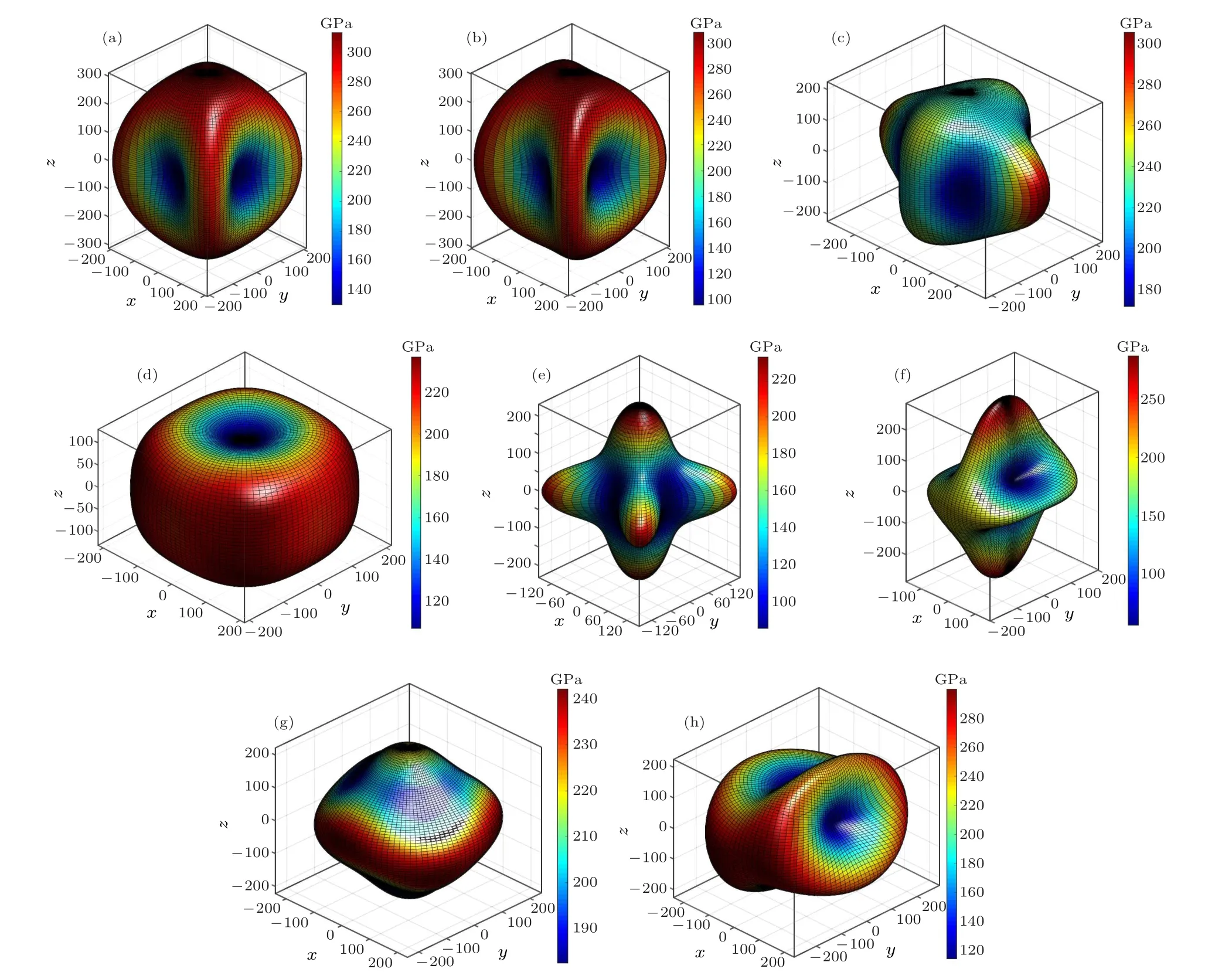
Fig.4. Directional dependence of Young’s modulus(in GPa)of(a)P42/mnm,(b)Pnnm,(c)Cmcm,(d)P4/nmm,(e)I4/mcm,(f)P21/m,(g)Pm1,and(h)C2/m phases at 0 GPa.
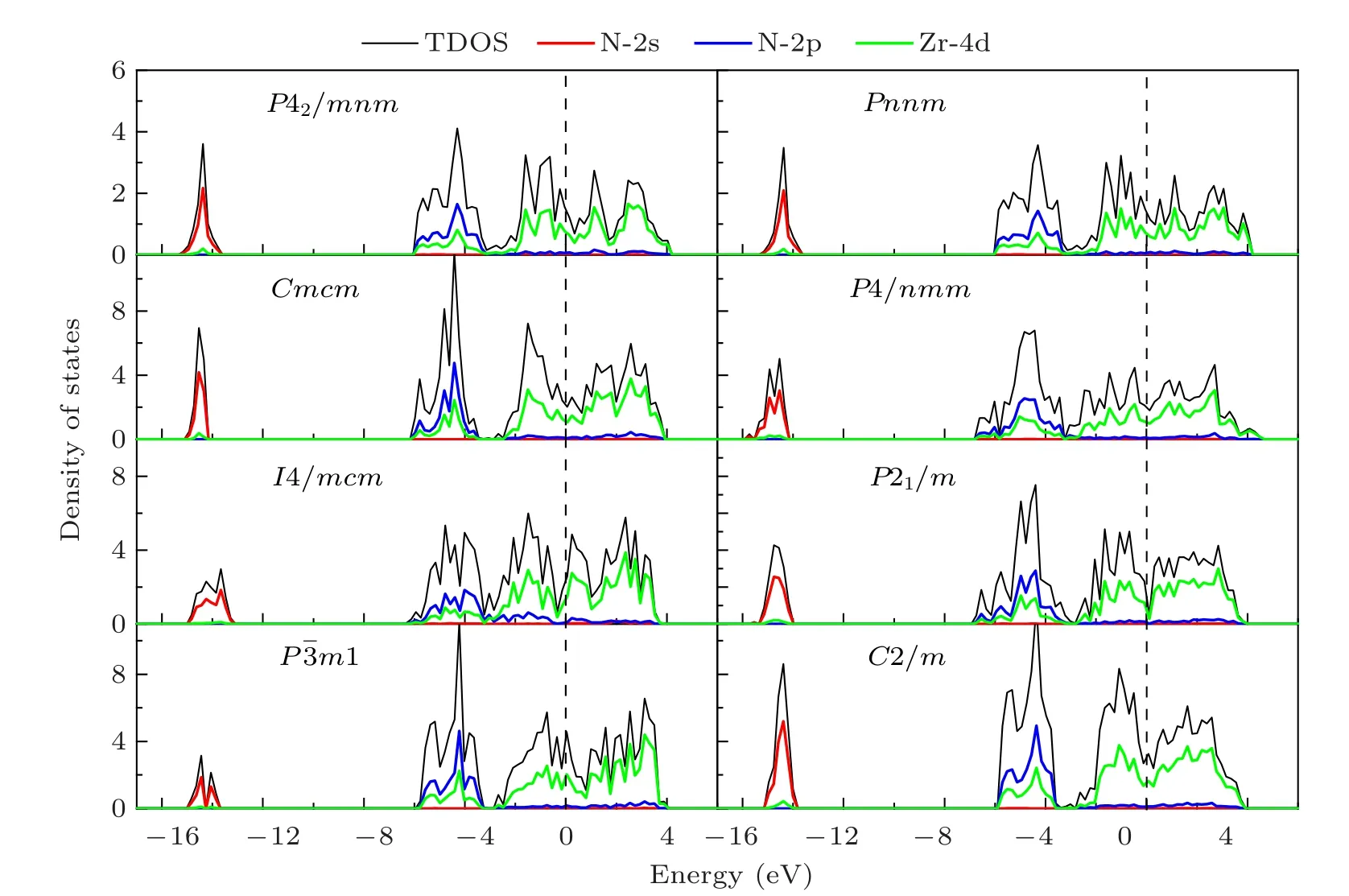
Fig.5. Projected density of states(DOS)of Zr2N compounds at ambient pressure,showing the partial DOS of the N 2s(red line)and N 2p(blue line)orbitals,the Zr 4d orbital(green line),and the total DOS(black line).
4. Conclusion
In summary, the pressure-dependent phase diagram of zirconium heminitride is investigated using ab initio evolutionary algorithm methods. Five novel high-pressure phases(i.e., P4/nmm, I4/mcm, P21/m, Pm1, and C2/m) of Zr2N are predicted in the present study. As the pressure increases from 0 GPa to 200 GPa,Zr2N moves sequentially through the phases as P42/mnm→Pnnm →Cmcm →P4/nmm→I4/mcm at the corresponding transition pressures of 6.5 GPa,16.3 GPa,55.2 GPa,and 144.4 GPa,respectively.The calculated phonon spectra reveal that all candidate Zr2N structures are dynamically stable at ambient pressure. According to the calculated elastic constants, all predicted Zr2N configurations are expected to be mechanically stable at atmospheric pressure.Although the eight candidate configurations possess identical chemical composition ratios, their mechanical properties exhibit considerable differences. Excepting the Cmcm phase,the Zr2N structures are ductile materials,among which the I4/mcm phase is the most ductile configuration. At atmospheric pressure, the Vickers hardness of the Zr2N compounds is ordered as Cmcm >P42/mnm >C2/m >P4/nmm >Pm1 >Pnnm >P21/m >I4/mcm. The calculated electronic structures demonstrate that the high mechanical strength and hardness of the Cmcm phase originate from the strong hybridization of the N-2p states and Zr-4d states, while the weaker interactions between the Zr and N atoms are likely responsible for the weaker mechanical behaviors of I4/mcm-Zr2N. These results provide important additional insight into the structureproperty relationships of TM heminitrides and the development of practical applications for Zr2N.
Acknowledgment
We thank Sara Maccagnano-Zacher, PhD, from Liwen Bianji, Edanz Editing China (www.liwenbianji.cn/ac), for editing the English text of a draft of this manuscript.
- Chinese Physics B的其它文章
- Two-dimensional finite element mesh generation algorithm for electromagnetic field calculation*
- Stable water droplets on composite structures formed by embedded water into fully hydroxylated β-cristobalite silica*
- Surface active agents stabilize nanodroplets and enhance haze formation*
- Synchronization mechanism of clapping rhythms in mutual interacting individuals*
- Theoretical study of the hyperfine interaction constants,Land′e g-factors,and electric quadrupole moments for the low-lying states of the 61Niq+(q=11,12,14,and 15)ions*
- Ultrafast photoionization of ions and molecules by orthogonally polarized intense laser pulses: Effects of the time delay*