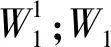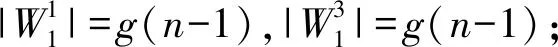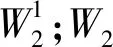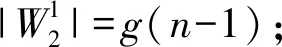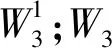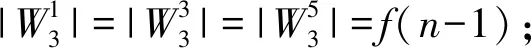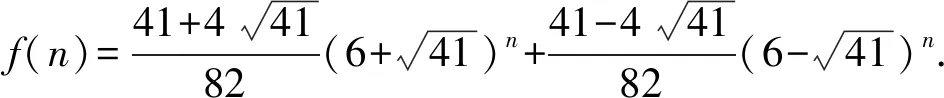唐保祥,任 韓

(1.天水師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,甘肅 天水 741001)(2.華東師范大學(xué)數(shù)學(xué)系,上海 200062)

圖的完美對(duì)集計(jì)數(shù)理論是近30年來圖論研究的熱點(diǎn)問題之一[1-6]. 對(duì)于存在完美對(duì)集的圖,把完美對(duì)集按照關(guān)聯(lián)某個(gè)頂點(diǎn)的邊進(jìn)行分類,求出每一類完美匹配數(shù)目的遞推關(guān)系式,再把各類完美對(duì)集的遞推式相加,就得到一組有相互聯(lián)系的遞推關(guān)系式,利用這些遞推式之間的相互關(guān)系,消去那些不需要的遞推關(guān)系式,從而得到這個(gè)圖的完美對(duì)集數(shù)目的遞推關(guān)系式,最后求出這個(gè)遞推式的通解,進(jìn)而就得到這個(gè)圖的完美對(duì)集數(shù)目的顯式公式[7-14]. 這個(gè)方法為圖的完美對(duì)集理論的應(yīng)用提供了支持.

1 基本概念

定義1若圖G有一個(gè)1-正則生成子圖,則稱這個(gè)生成子圖為圖G的完美對(duì)集.

定義2設(shè)圖G是一個(gè)有完美對(duì)集的圖,若圖G的兩個(gè)完美對(duì)集W1和W2中有一條邊不同,則稱W1和W2是G的兩個(gè)不同的完美對(duì)集.

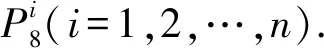
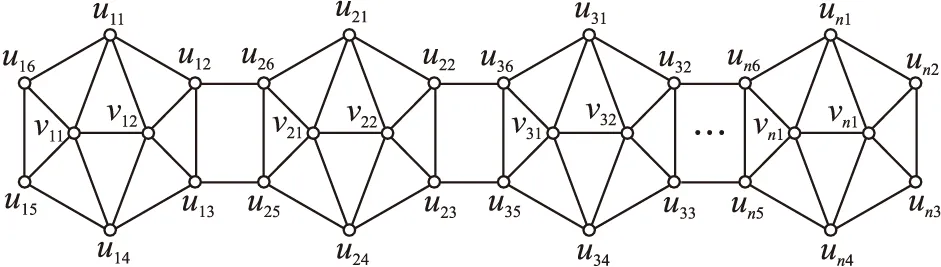
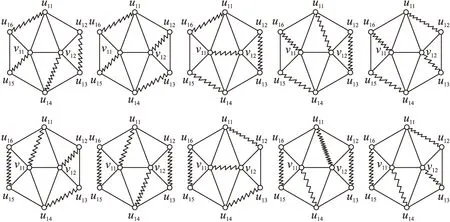
圖1 圖2-nP8Fig.1 Figure of 2-nP8

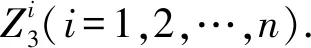
圖2 圖2-nZ3Fig.2 Figure of 2-nZ3

2 主要結(jié)果

定理1設(shè)圖2-nP8的完美對(duì)集數(shù)為f(n),則

證明容易看出圖2-nP8有完美對(duì)集. 為了計(jì)算f(n)的表達(dá)式,先定義一個(gè)圖G1. 把路xy的端點(diǎn)x,y分別與圖2-nP8的頂點(diǎn)u16,u15連接一條邊得到的圖記為G1,如圖3所示.

圖3 圖G1Fig.3 Figure of G1

容易看出圖G1有完美對(duì)集. 設(shè)圖G1的完美對(duì)集數(shù)為g(n),圖G1的完美對(duì)集集合為W,按照W中元素飽和頂點(diǎn)x的情況可分兩類:設(shè)W中包含邊xy的完美對(duì)集集合為W1,W中包含邊xu16的完美對(duì)集集合為W2,根據(jù)不同完美對(duì)集的定義知,W1∩W2=φ,W=W1∪W2,故g(n)=|W|=|W1|+|W2|.

因?yàn)閤y∈W1,故xu16,yu15?W1,由f(n)的定義知,|W1|=f(n).

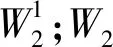
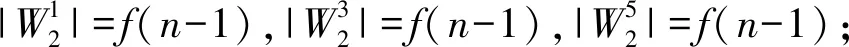
故

g(n)=f(n)+3f(n-1)+2g(n-1).

(1)

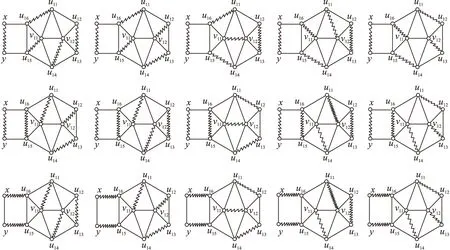
再求f(n)的遞推式. 設(shè)圖2-nP8的完美對(duì)集集合為W,圖2-nP8包含邊u16u11,u16v11,u16u15的完美對(duì)集集合分別為W1,W2,W3,則Wi∩Wj=φ(1≤i

綜上所述,

f(n)=5f(n-1)+5g(n-1).

(2)

由式(1),得

g(n-1)=f(n-1)+3f(n-2)+2g(n-2),

(3)

把式(3)代入(2),得

f(n)=10f(n-1)+15f(n-2)+10g(n-2),

(4)

由式(2),得

f(n-1)=5f(n-2)+5g(n-2),

(5)

由式(4)和(5)消去g(n-2),得

f(n)=12f(n-1)+5f(n-2).

(6)

由圖4知,f(1)=10.

圖4 圖G2Fig.4 Figure of G2

由圖5知,g(1)=15.

所以由式(2),得f(2)=125.

圖5 圖G3Fig.5 Figure of G3

定理2設(shè)圖2-nZ3的完美對(duì)集數(shù)為φ(n),則

證明容易看出圖2-nZ3有完美對(duì)集. 為了計(jì)算φ(n)的表達(dá)式,先定義一個(gè)圖G4. 把路wt的端點(diǎn)w,t分別與圖2-nZ3的頂點(diǎn)u11,u13連接一條邊得到的圖記為G4,如圖6所示.

圖6 圖G4Fig.6 Figure of G4

容易看出圖G4有完美對(duì)集. 設(shè)圖G4的完美對(duì)集數(shù)為h(n),圖G4的完美對(duì)集集合為N,按照N中元素飽和頂點(diǎn)w的情況可分兩類:設(shè)N中包含邊wt的完美對(duì)集集合為N1,N中包含邊wu11的完美對(duì)集集合為N2,根據(jù)不同完美對(duì)集的定義知,N1∩N2=φ,N=N1∪N2,故h(n)=|N|=|N1|+|N2|.

因?yàn)閣t∈N1,故wu11,tu13?N1,由φ(n)的定義知,|N1|=φ(n).

因?yàn)閣u11∈N1,所以tu13,v11v13,v12u12∈N2,由φ(n)的定義知,|N2|=φ(n-1).

故

h(n)=φ(n)+φ(n-1).

(7)

再求φ(n)的遞推式. 設(shè)圖2-nZ3的完美對(duì)集集合為N,圖2-nZ3包含邊u13u11,u13v13,u13u12的完美對(duì)集集合分別為N1,N2,N3,則Ni∩Nj=φ(1≤i

因?yàn)閡11u13∈N1,故v11v13,v12u12∈N1,由φ(n)的定義知,|N1|=φ(n-1).

故|N2|=φ(n-1)+h(n-1).

因?yàn)閡13u12∈N3,故v12v13,u11v11∈N3,由φ(n)的定義知,|N3|=φ(n-1).

所以

φ(n)=3φ(n-1)+h(n-1).

(8)

由式(7)和(8),得

φ(n)=4φ(n-1)+φ(n-2).

(9)

由圖7知,φ(1)=4.

圖7 圖G5Fig.7 Figure of G5

由圖8知,h(1)=5.

圖8 圖G6Fig.8 Figure of G6

由式(8),得φ(2)=17.