石煥南,鄭小彬,王東生

(1.北京聯(lián)合大學(xué) 師范學(xué)院,北京 100011;2.福建泉州桃李教育咨詢有限責(zé)任公司,福建 泉州 362000;3.北京電子科技職業(yè)學(xué)院 基礎(chǔ)部,北京 100176)

1 預(yù)備知識

定理已知x,y為正實(shí)數(shù),n為正整數(shù),若x2n+1+y2n+1≥2,則

這個(gè)由意大利學(xué)者Francesco Cavazzan提出的不等式,雖然形式簡潔,但證明起來并不輕松.本文利用受控理論[1]和分析方法給出四種不同的證明.

為此給出必要的定義與引理.設(shè) ?n,?n+和 ?n++分別表示n維實(shí)數(shù)集,n維非負(fù)實(shí)數(shù)集和n維正實(shí)數(shù)集,并記?1=?,?1+=?+和 ?1++=?++.對于x=(x1,x2,…,xn) ∈?n,將x的分量排成遞減的次序后,記作x［1］≥x［2］≥…≥x［n］.

定義1[2,3]設(shè)x=(x1,x2,…,xn)和y=(y1,y2,…,yn) ∈?n.若

且

則稱x被y所控制,記作x?y.

定義2[2,3]設(shè) Ω??n,若在Ω上,

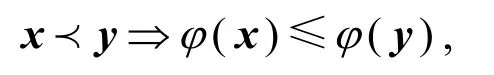
則稱φ為Ω上的Schur凸函數(shù),簡稱為S-凸函數(shù);若-φ是Ω上的S-凸函數(shù),則稱φ為Ω上的S-凹函數(shù).

楊鎮(zhèn)杭[4]定義了Schur-f凸函數(shù)及Schur-冪凸函數(shù),并研究它們的性質(zhì)及判定.

定義3[4](a) 設(shè)f:?++→?是嚴(yán)格單調(diào)函數(shù),Ω??n,n≥2.若對于任何x,y∈Ω,總有

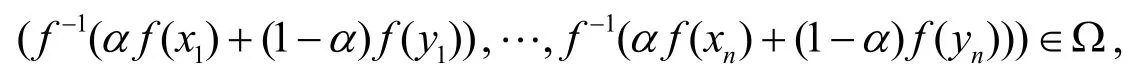
則稱Ω是f-凸集,其中α∈ [0,1]且α+β=1;

(b) 設(shè) Ω??n,其內(nèi)部非空.φ:Ω→?+,對于任意x,y∈Ω,若

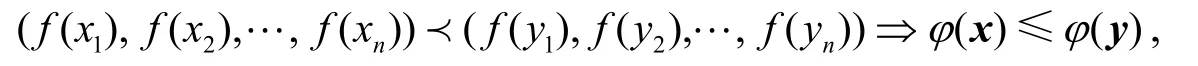
則稱φ為Ω上的S-f凸函數(shù);若φ-是Ω上的S-f凸函數(shù),則稱φ為Ω上的S-f凹函數(shù).

定義4在定義3中,若取

則稱φ為Ω上的m階S-冪凸函數(shù);若φ-是Ω上的m階S-冪凸函數(shù),則稱φ為Ω上的m階S-冪凹函數(shù).

注在定義4中取f(x)=x可得S-凸函數(shù)的定義.

引理1[4]設(shè)Ω??是帶有非空內(nèi)部Ω°的對稱集,φ:Ω→?在Ω上連續(xù)且在Ω°上可微,則φ在Ω上Schur m-冪凸(Schur m-冪凹),當(dāng)且僅當(dāng)φ在Ω上對稱且?x∈Ω°(x1≠x2),有

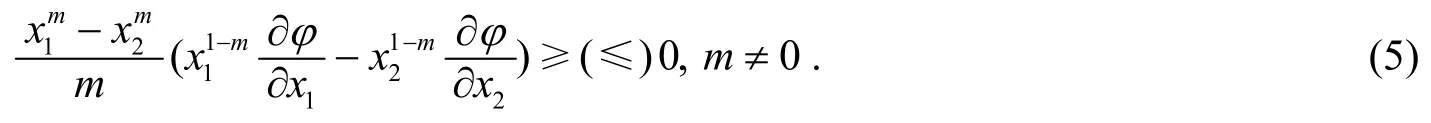
對于m≠0,因

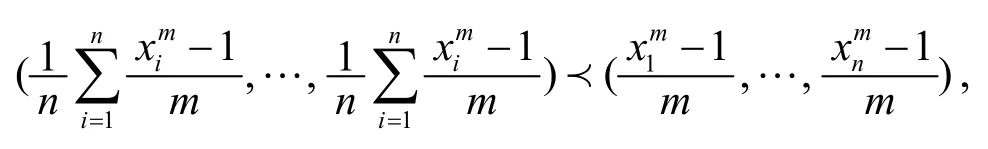
即

若φ在Ω上Schur m-冪凸(Schur m-冪凹),則

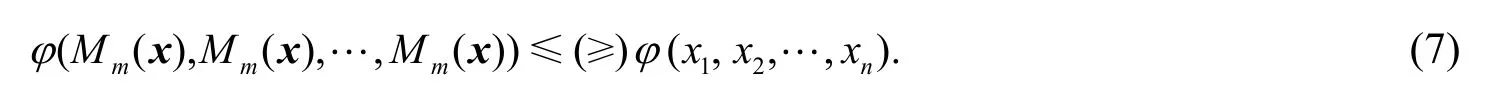
定義5設(shè)(r,s)∈?2,(x,y) ∈,定義二元Gini平均為:

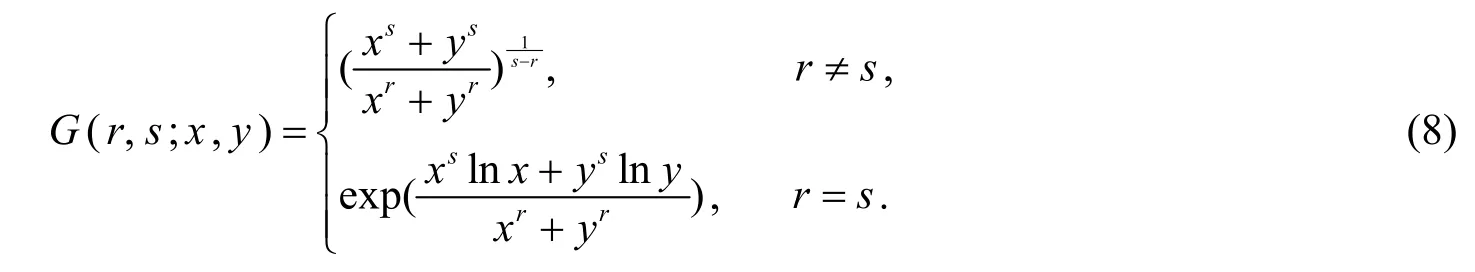
引理2[5]對于固定的(x,y)∈?2+且x≠y,G(r,s;x,y)在 ?2+上關(guān)于(r,s)Schur-凹,在 ?2-上關(guān)于(r,s)Schur-凸.

引理3(Gini平均比較定理)[6]設(shè)x,y∈ ?++,p,q,r,s∈?,(p-q)(r-s)≠0,則

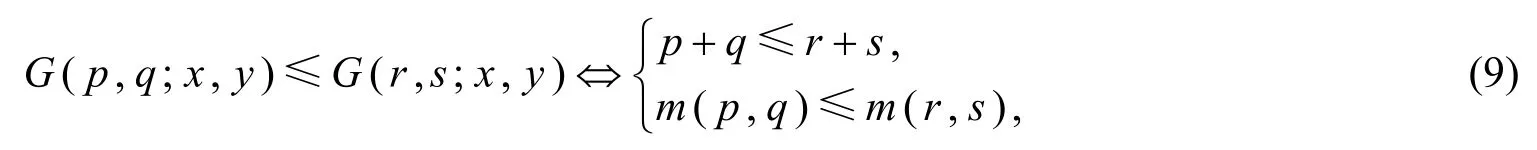
其中

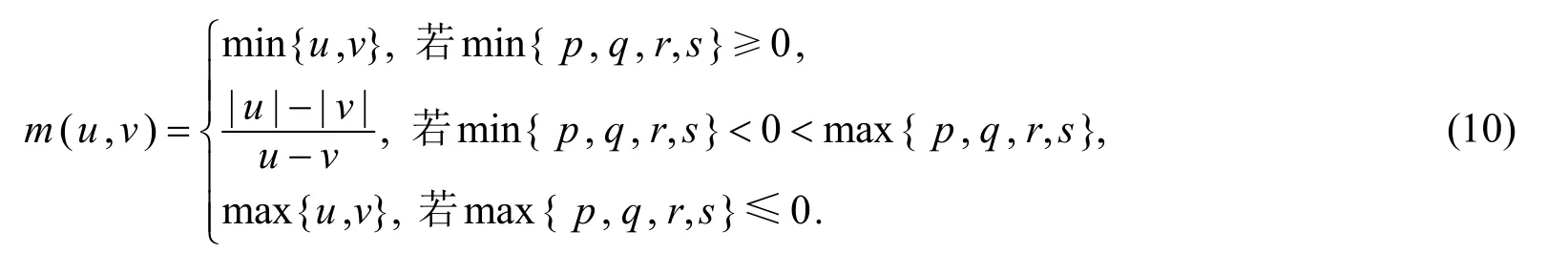
2 定理的證明

證法1令

分兩步證明.

(I) 若x2n+1+y2n+1=2,此時(shí),由冪平均的單調(diào)性,有

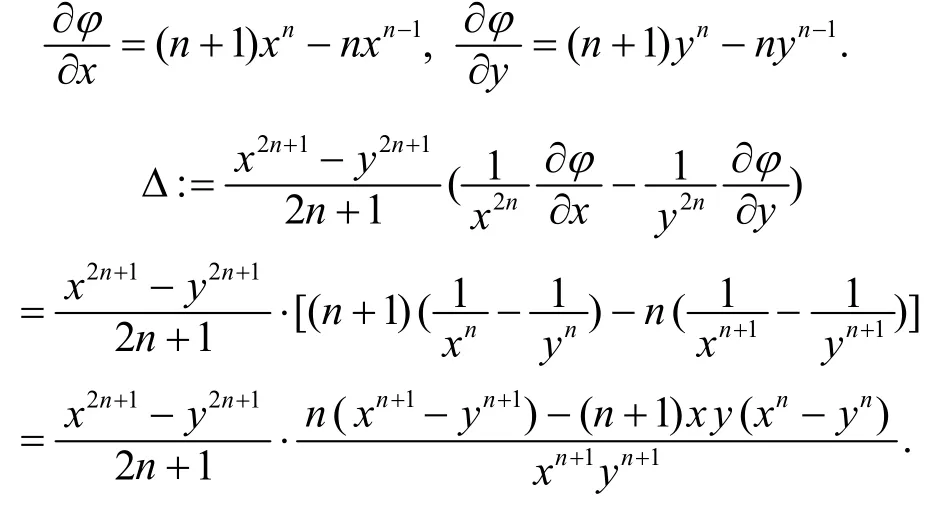
欲證Δ≥0,只需證n(xn+1-yn+1)≥(n+1)xy(xn-yn),即

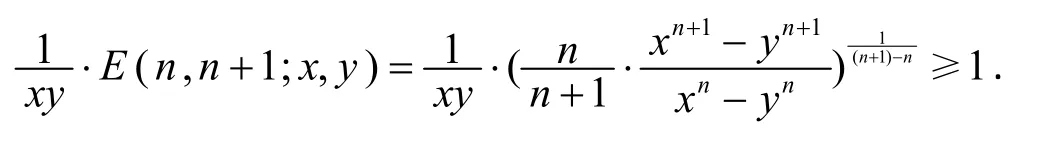
由文[1]定理1.1知,E(n,n+1;x,y)在上Schur-凸,故

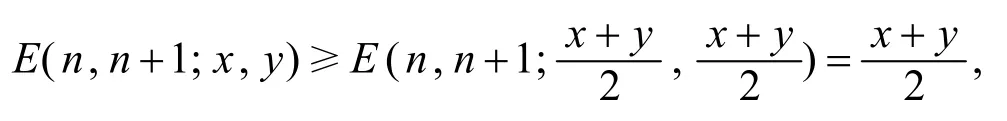
從而

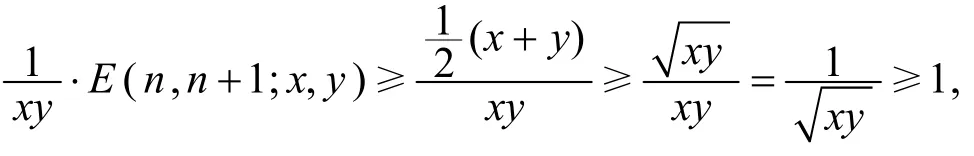
故Δ≥0,由引理1,φ是上的2m+1階S-冪凸函數(shù),從而

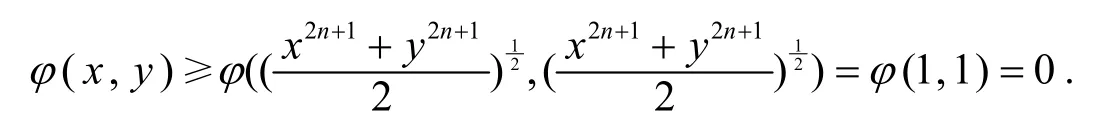
(II) 若x2n+1+y2n+1=a＞2,則

由(I)有

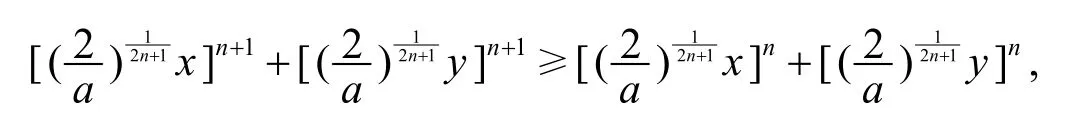
即

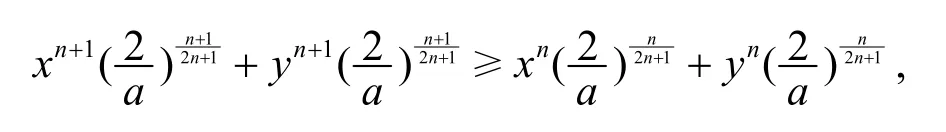
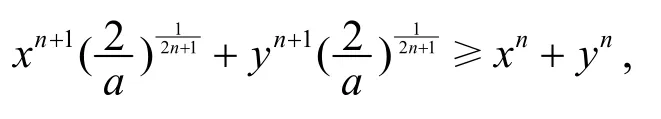
證法2據(jù)引理2,G(r,s;x,y)在 ?2+上關(guān)于(r,s)Schur-凹,由(n+1,n)?(2n+1,0),有

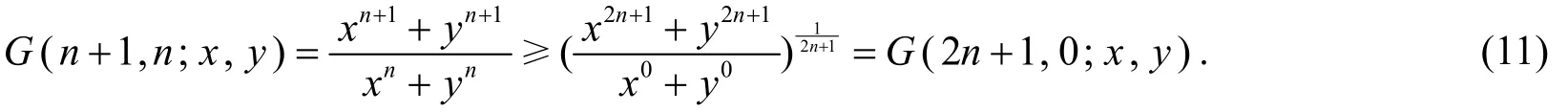
結(jié)合條件x2n+1+y2n+1≥2即得證.

證法3所證不等式等價(jià)于

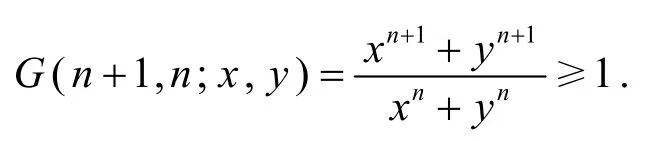
由條件x2n+1+y2n+1≥2,只需證

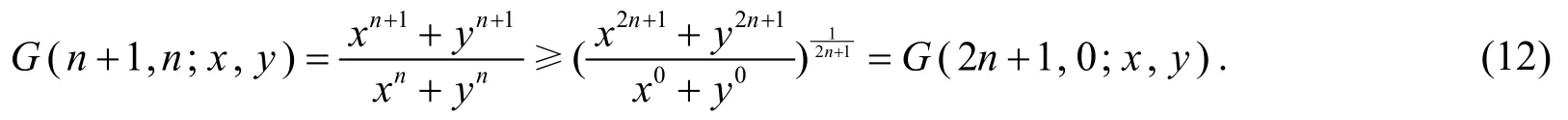
因n+1+n=2n+1+0,且min{n+1,n}=n＞min{2n+1,0}=0,由引理3知不等式(12)成立.

證法4不妨設(shè)x≥y,令x=ty,則t≥1.于是條件x2n+1+y2n+1≥2化為

因xn+1+yn+1≥xn+yn等價(jià)于只需證

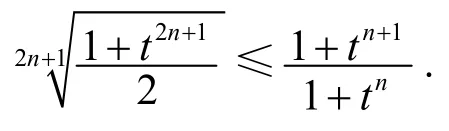
令

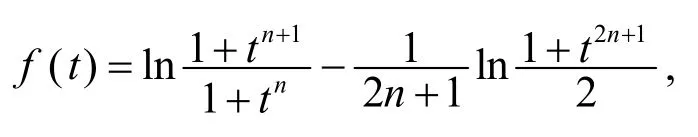
則

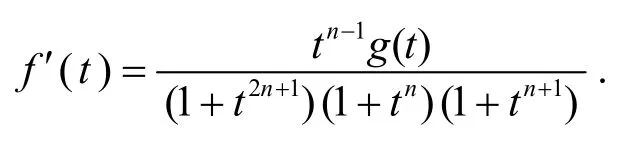
其中

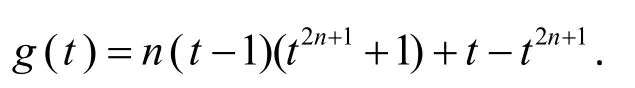
因

g(t)≥g(1)=0,故f′(t)≥0,進(jìn)而f(t)≥f(1)=0,由此得證.