Chao JIANG (蔣超) Zuhan LIU (劉祖漢) Ling ZHOU (周玲)

School of Mathematical Science,Yangzhou University,Yangzhou 225002,China

E-mail: jiangchao950319@outlook.com;zhliu@yzu.edu.cn;zhoul@yzu.edu.cn

Abstract In this paper,a fractional Laplacian mutualistic system under Neumann boundary conditions is studied.Using the method of upper and lower solutions,it is proven that the solutions of the fractional Laplacian strong mutualistic model with Neumann boundary conditions will blow up when the intrinsic growth rates of species are large.

Key words mutualistic system;fractional Laplacian;Neumann boundary;upper and lower solutions;blow-up

1 Introduction

In 2017,Dipierro,Ros-Oton and Valdinoci [6] introduced the following Neumann problem for the fractional Laplacian:

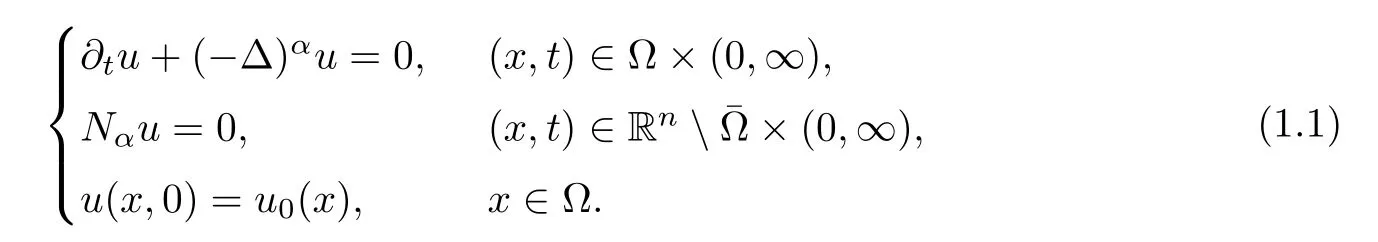
Here Ω is a bounded Lipschitz domain of Rnwithn≥1.Nαis a “nonlocal normal derivative”,given by

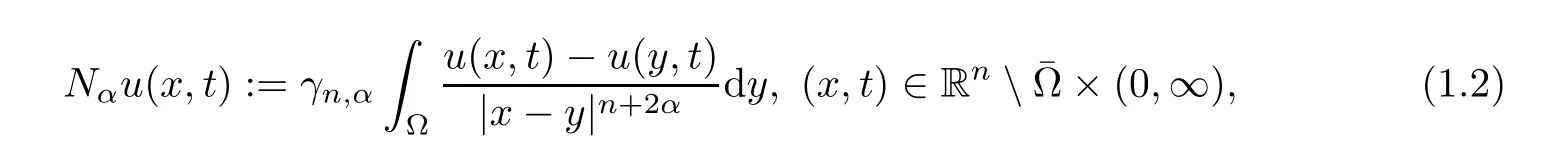
γn,αis a constant that appears in the definition of fractional Laplacian operator

The article [6] was devoted to studying the solutions of (1.1) with the following properties:conservation of mass inside Ω,decreasing energy,and convergence to a constant ast→∞.In addition,for the elliptic case,the variational formulation of the problem and the existence of solutions were given.Regarding the Neumann problems for the fractional Laplacian,readers can refer to [1–3,5–10,15–18] and the references therein.

In 1992,Pao [19] discussed a cooperating two-species Lotka-Volterra model

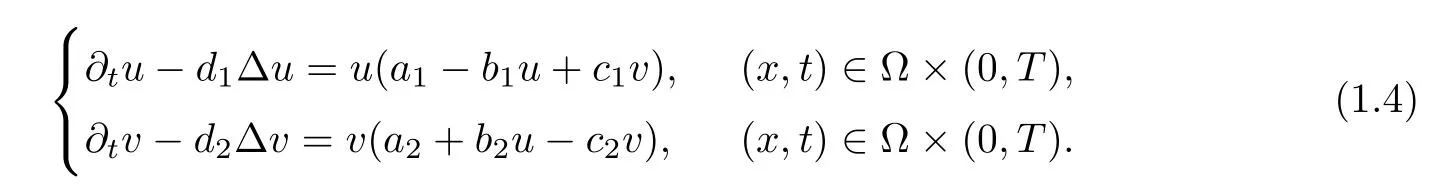
Pao showed that the solution of (1.4) under the Dirichlet or Robin boundary conditions with any nonnegative initial data is unique and global,while the blow-up solutions of (1.4) are possible when the two species are strongly mutualistic (b2c1＞b1c2),which means that the geometric mean of the interaction coefficients exceeds that of population regulation coefficients.

In this paper,we use the method of upper and lower solutions to deal with the blow-up problems of the following two-species fractional Laplacian mutualistic system with the Neumann boundary conditions:

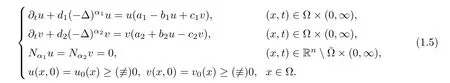
Hereu(x,t) andv(x,t) represent the population densities of two mutualistic species.The positive constantsd1andd2are dispersal rates ofuandv,respectively.The real numbersai(i=1,2) represent the intrinsic growth rates of the two species.The parametersb1,c2＞0 are interspecific competition coefficients and the parametersb2,c1＞0 are interspecific cooperations coefficients.u0(x) andv0(x) are continuous functions forx∈Ω.

Our main purpose is to study the influence of fractional Laplacian and Neumann boundary conditions on the blow-up of the solutions.To this end,we first establish the comparison principle.Since the fractional Laplacian is different from the classical case and a new definition of the Neumann boundary is given,the classical comparison principle is not applicable here.To overcome these difficulties,we give the definition of weak upper and weak lower solutions,and establish the comparison principle.

Next,we extend the blow-up properties of solutions to the fractional Laplacian mutualistic system under the Neumann boundary conditions.Employing the comparison principle,we obtain the following result:

Theorem 1.1Ifb1c2＜b2c1holds,then we have the following blow-up properties: if min＞0 andα1=α2:=α,the solutions of (1.5) blow up for any nontrivial initial data satisfying that for allx∈Ω,min{u0(x),v0(x)}＞0.

This rest of this paper is arranged as follows: in Section 2,we give the definition of weak upper solutions and weak lower solutions,and establish the comparison principle to system(1.5).In Section 3,we give sufficient conditions for the blow-up of the solutions for problem(1.5).

2 Preliminary

In this section,we give some definitions and establish the comparison principles for our system.

Definition 2.1Given a measurable functionu: Rn→R,we set

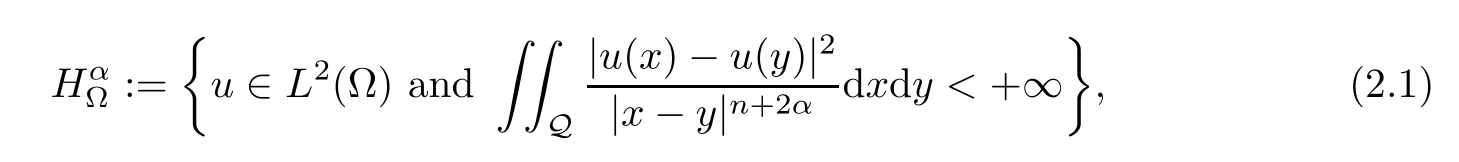
where Q :=(Ω × Ω) ∪((Rn Ω) × Ω) ∪(Ω ×(Rn Ω)).

Combining (2.5) with (2.6),we have that

Here,we denote byCa constant depending on the structural parameters.By Cauchy’s inequality,we have that

Substituting (2.8) into (2.7),we have that

Combining (2.9) with (2.10),we obtain that

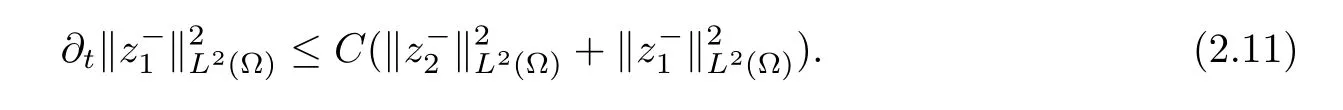
Similarly,we can obtain that

Next,adding up the two inequalities,we deduce that

3 Blow-up

In this section,whenα1=α2:=α∈(0,1),sufficient conditions for the blow-up of the solutions of (1.5) are established.

The following lemma plays a crucial role in Theorem 3.2:

Lemma 3.1Assume thatφ(x) ∈.Consider the eigenvalue problem

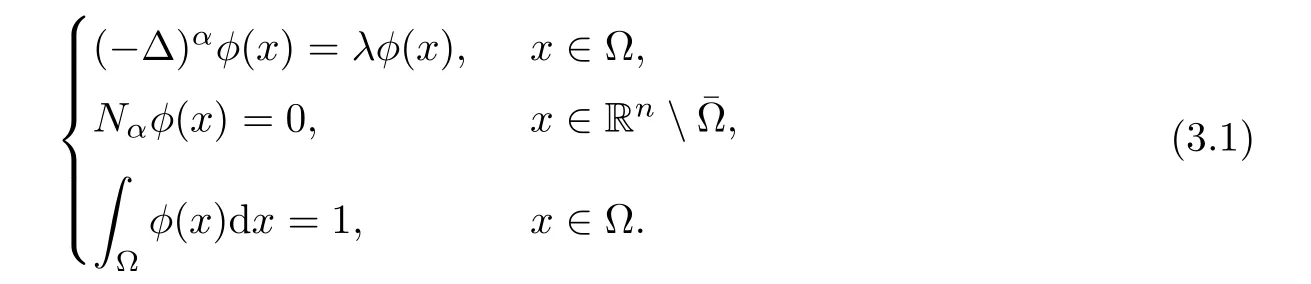
Ifφ(x) is a weak solution of (3.1),then

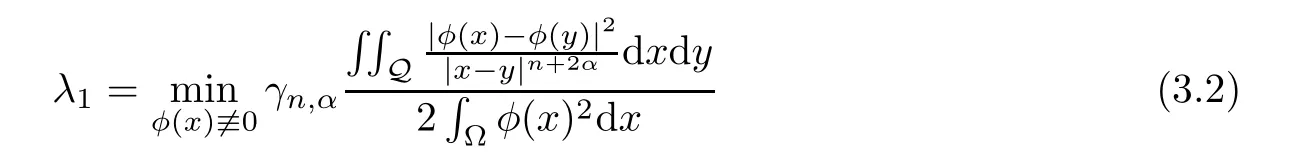
and Φ1(x)＞0 satisfy (3.1) and (3.2).λ1and Φ1(x) are called the first eigenvalue and eigenfunction of (3.1).Moreover,λ1=0.

ProofWe omit the proof here;interested readers can see [15] for more details. □

Theorem 3.2Letw(x,t) ∈L2([0,T];),?tw(x,t) ∈L2((0,T);L2(Ω)) be a nonnegative weak solution of the problem whered,α,aandbare constants and satisfyα∈(0,1),d ＞0 andb ＞0.Then we can get the following blow-up properties:

(i) ifa≥λ1,for any nontrivial nonnegative initial data,the solutions of (3.3) blow up;

(ii) ifa ＜λ1,for large enough initial data,the solutions of (3.3) blow up.

ProofDefine

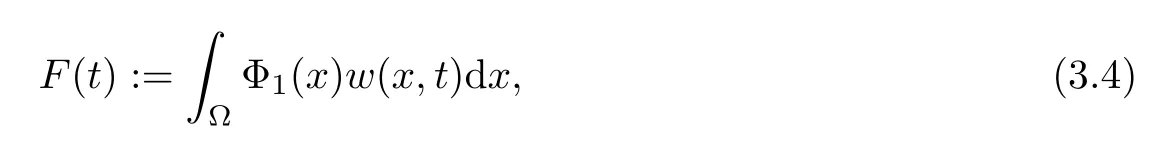
where Φ1(x) is given by Lemma 3.1.We take Φ1(x) as a test function.DerivingF(t) with respect totand using (3.3),we obtain that

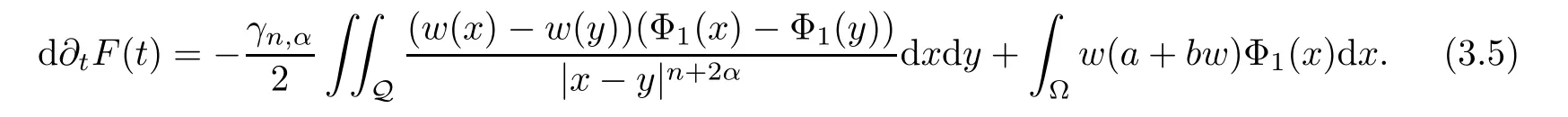
By Lemma 3.1,we have that

where the last inequality follows from Hlder’s inequality.

(i) In the casea≥λ1,from (3.6),for any nontrivial nonnegative initial data,we have thatF(t) blows up.

(ii) In the casea ＜λ1,we can choose sufficiently large initial dataw(x,0) such that

It follows from (3.6) thatF(t) blows up for sufficiently large initial data. □

The proof of Theorem 1.1Now,we are going to prove Theorem 1.1.To do this,it suffices to construct a weak lower solution of (1.5) that blows up at a finite timeT.Letw(x,t) ∈L2,?tw(x,t) ∈L2((0,T);L2(Ω)) be a nonnegative function satisfyingNαw(x,t)=0 for (x,t) ∈Rn× (0,T].We definewhereδ1,δ2are some positive constants to be determined later.In what follows,we will prove that,in fact the weak lower solution (δ1w(x,t),δ2w(x,t)) exists.In order to guarantee that (δ1w(x,t),δ2w(x,t)) is a weak lower solution of (1.5) in Ω × [0,T],we need to proveδ1w(x,0) ≤u0(x),δ2w(x,0) ≤v0(x) in Ω and,for any (x,t) ∈Ω ×(0,T],

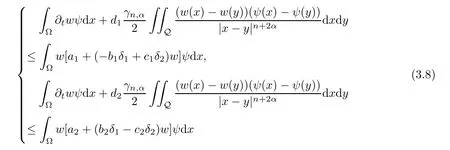
Therefore,by choosingwas a solution of the initial value problem

and by calculating,we can get thatw ＞0 fort∈(0,T].According to the positivity ofw,a,bandd,we can easily obtain that?tw ＞0 fort∈(0,T].Thus (3.8) is satisfied.We chooseεenough small such thatδ1＜1 andδ2＜1,which guarantees that

Hence,we arrive at the fact thatis a weak lower solution of (1.5).By using(i) of Theorem 3.2 and Lemma 3.1 withλ1=0 tow,we have thatblows up.Furthermore,by Lemma 2.3 (the comparison principle),the solutions of system (1.5) blow up.

□