School of Mathematics and Statistics,Hubei Key Laboratory of Mathematical Sciences,Central China Normal University,Wuhan 430079,China

E-mail: aissaoui.narimene@mails.ccnu.edu.cn

Wei LONG (龍薇)?

College of Mathematics and Information Science, Jiangxi Normal University,Nanchang 330022, China

E-mail: lwhope@jxnu.edu.cn

Abstract This paper deals with the existence of positive solutions to the following nonlinear Kirchhoffequation with perturbed external source terms: Here a,b are positive constants,V (x),Q(x) are positive radial potentials,1 ＜p ＜5,ε＞0 is a small parameter,f(x) is an external source term in L2(R3) ∩L∞(R3).

Key words nonlinear Kirchhoffproblem;Lyapunov-Schmidt reduction;positive solutions;level set

1 Introduction

In this paper,we consider the following nonlinear Kirchhoffequation with perturbed external source terms:

Herea,bare positive constants,V(x) andQ(x) are positive radial potentials,1＜p ＜5,ε ＞0 is a small parameter,andf(x) is an external source term inL2(R3) ∩L∞(R3).

Owing to the appearance of the termΔu,problem (1.1) is nonlocal.Consequently,problem (1.1) is no longer a pointwise identity.This leads to some mathematical difficulties and makes studying such issues more interesting.Indeed,ifV(x)=0 and R3is replaced by a bounded domain Ω ∈R3,then problem (1.1) becomes the KirchhoffDirichlet problem

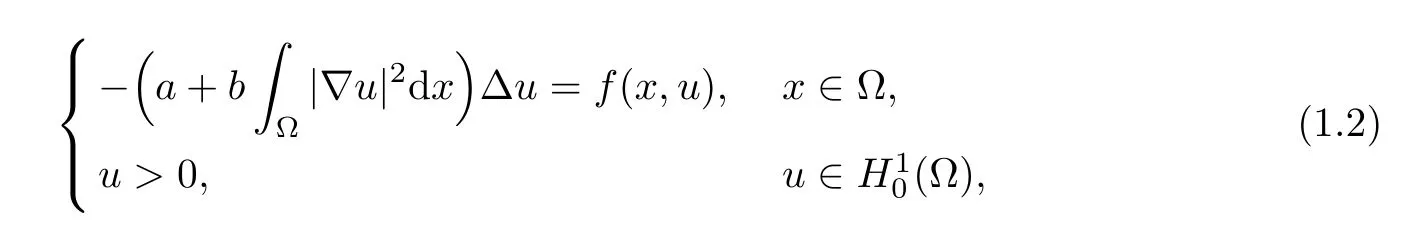
wherea,b ＞0 are constants.

Problem (1.2) is related to the stationary analogue of the equation

which was proposed by Kirchhoffin [19] as an extension of the classical d’Alembert’s wave equation for the vibration of elastic strings.Kirchhoff’s model takes into account the changes in length of the string produced by tranverse vibrations,so the nonlocal term appears.We refer to [8,29] for physical and numerical aspects of Kirchhoff’s model.Many interesting works on Kirchhoffequations can be found,for example,Arosio and Panizzi [4],Bernstein [6],Lions [21],and Pohozaev [30].

Since Lions proposed in [21] an abstract functional analysis framework to the equation

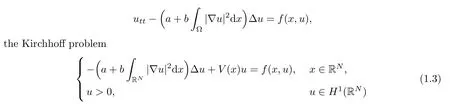
in RN(N=1,2,3) has been extensively studied.For whenVandfsatisfy different conditions,many interesting results on the existence and multiplicity of solutions to (1.3) have been obtained;see [2,3,10,15,16,22,24,31–34].Li et al.[20] focused on the problem

for when 1＜p ＜5.They first established a uniqueness and non-degeneracy result of positive solutions to (1.4) and then proved the existence of positive peak solutions to the related perturbed problem

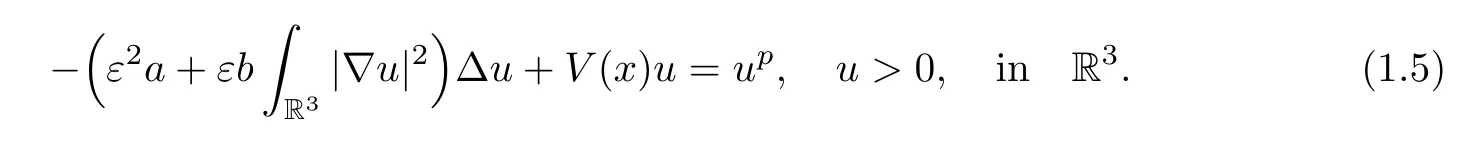
In [24],Luo,Peng and Wang proved the existence of positive multi-peak positive solutions of (1.5) whenV(x) satisfies some suitable assumptions.In [16],Hu and Shuai also obtained multiple positive solutions to this type of perturbation problem with general nonlinearity under some precise hypotheses.For more results,we refer to the recent papers [7,25–27].

From the mathematical point of view,Schrdinger equations are special cases of Problems(1.1) and (1.5).Indeed,whenb=0,Problem (1.5) is reduced to the classical Schrdinger equation

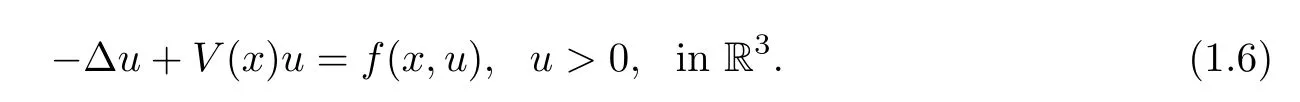
The classical nonlinear Schrdinger equation and the scalar field equation have been extensively studied in the last thirty years.A counterpart of Problem (1.6) may be the elliptic problem

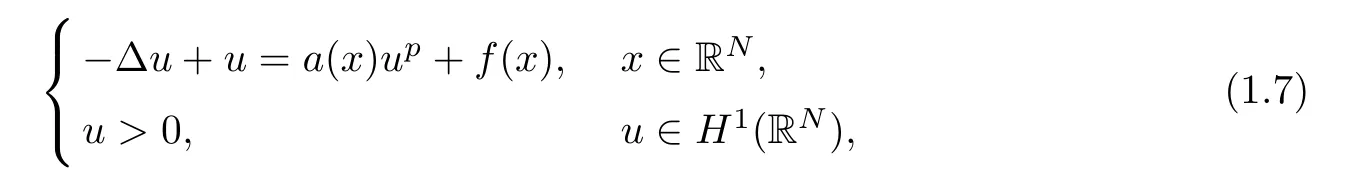
It is interesting whether or not positive solutions to (1.7) with a perturbationf(x) can survive this was studied in [1,9,17,35].For whena(x) ≥1,a(x)1 andf(x) ≡0,one can see that the Mountain Pass level is lower than the first level of the breaking down of the Palais-Smale condition.Hence,via the Mountain Pass Theorem,one can obtain a positive solution.Along these lines,in [9,17,35],a Mountain-Pass type of solution survives for (1.7) with the small perturbationf(x).For whenf(x)0 is small,the following interesting phenomena was observed in [1]: the Mountain Pass level is lower than the breaking down level of the Palais-Smale condition under the condition thata(x)-1 ≥-Ce-(2+δ)|x|.This is a consequence of the interaction phenomenon and it enables one to establish at least four positive solutions under the conditionsa(x)＞0,a(x) →1 as |x| →∞.

However,as far as we know,it seems that there are few results for the Kirchhoff-type problem (1.1) with perturbation.In this paper,inspired by Long and Peng [23],we intend to find that the Kirchhoff-type problem (1.1) with a perturbed term has one-bump positive solutions.Compared with the classical Schdinger equation,we cannot prove the existence of multi-bump solutions for problem (1),since the solutions of the limit Kirchhoffproblem have various decay rates with different numbers of bumps,which is also caused by the nonlocal term.

Our main idea is to use the radial ground stateUof

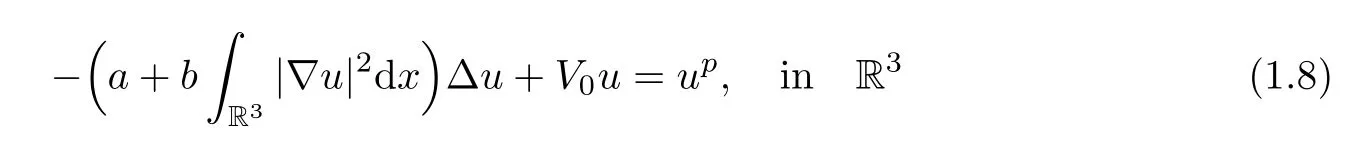
as the building block to construct positive single peak solutions,whereV0is a positive constant.From Li et al.([20]),we know that

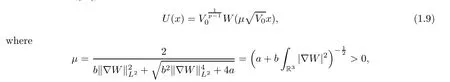
andW(x) is the unique solution of the equation

It is well-known thatW(x)=W(|x|) is non-degenerate (see [28]) and satisfies

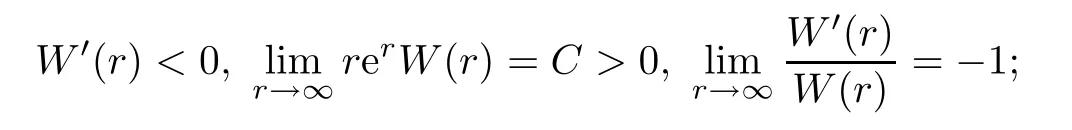
see [5] for an example.Thus,we haveU(x)=U(|x|),satisfying

Moreover,we get

Proposition 1.1(see [20]) There exists a unique positive radial solutionU∈H1(R3)satisfying that:

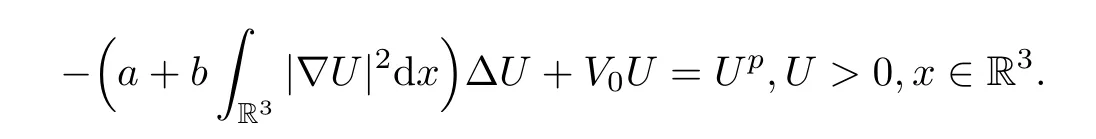
Moreover,Uis non-degenerate inH1(R3) in the sense that

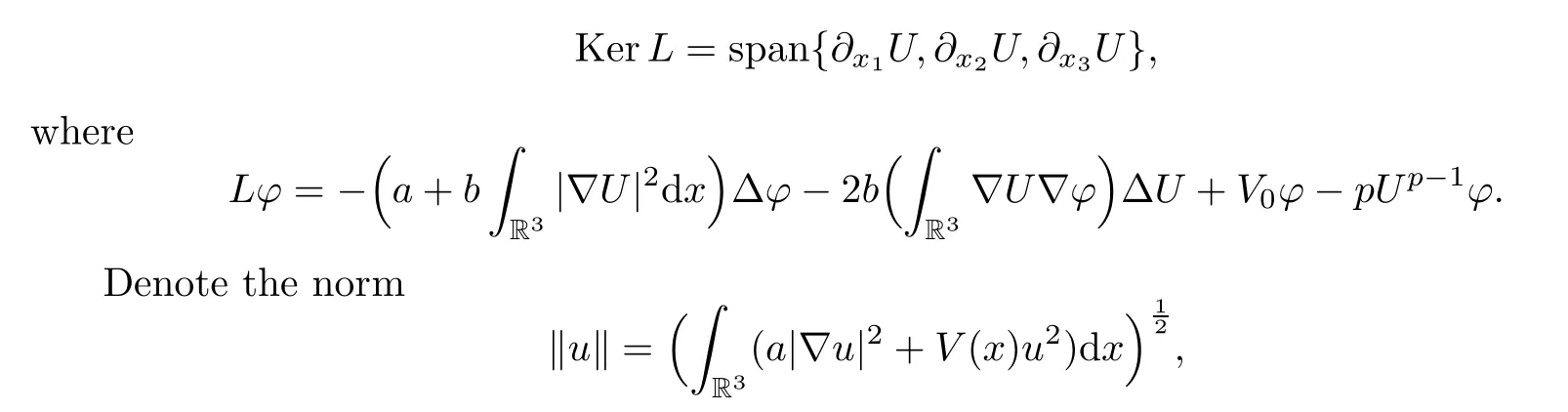
endowing it with the inner product

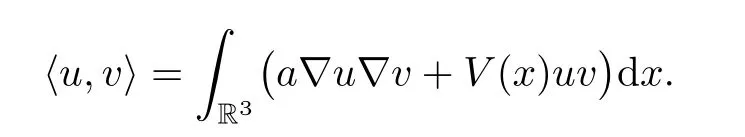
Moreover,define

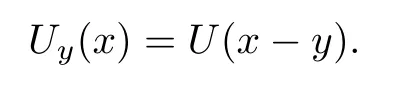
For any giveny∈R3,let

Throughout our paper,we assume thatV(x),Q(x) are radially symmetrical,and that the following assumptions hold:

· 0＜Q0(x) :=1 -Q(x)～Ce-sδ0|x|,?x∈R3;

· 0＜V0(x) :=V(x) -V0～Ce-s1δ0|x|,?x∈R3;

· |f(x)| ≤Ce-s2δ0|x|,?x∈R3.

Here 1＜s ＜p+1,1＜s1＜2 ands2＞1.

Our main results can how be stated as follows:

Theorem 1.2Under the assumptions on functionsV(x),Q(x) andf(x),there existsε0＞0 such that,for allε∈(0,ε0),problem (1.1) has at least two solutions of the form

where |yε| →+∞and ‖φε‖ →0 asε→0.

Under the assumptions onVandQ,the Palais-Smale condition may break down,hence it is extremely hard to obtain the existence or multiplicity results of positive solutions to(1.1) in the variational sketch.In the present paper,we will use the well-known Lyapunov-Schmidt reduction scheme and Lusternik-Schnirelman theory.It is worth emphasizing that the difficulties for using the Lyapunov-Schmidt reduction scheme here are caused by the complicated analysis for determining the main terms,since the potential functionsV(x) andQ(x) and the perturbationf(x) have different decay rates at infinity.On the other hand,the computations are much tougher,since Problem (1.1) involves the nonlocal term.

This paper is organized as follows: in Section 2,we will make an energy expansion for the function corresponding to Problem (1.1).We complete the proof of our main result in Section 3.

2 Some Technical Estimates and Energy Expansion

In this section,we will give some fundamental estimates for some integrals and the energy expansion.

Lemma 2.1IfH(x)0 is a nonnegative function and satisfies

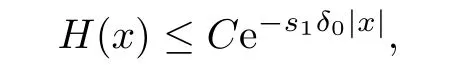
wheres1＞1,then,for any 1＜q ＜s1,there existC1andC2such that

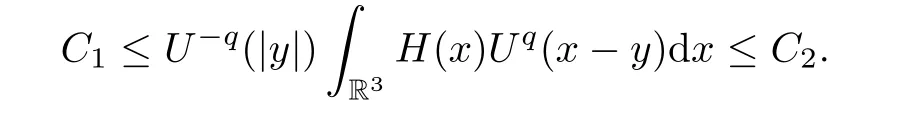
IfH(x) is a nonnegative radial function and satisfies

wheres ＞0,then,for any 0＜s ＜q,there exist some constantsC3andC4such that

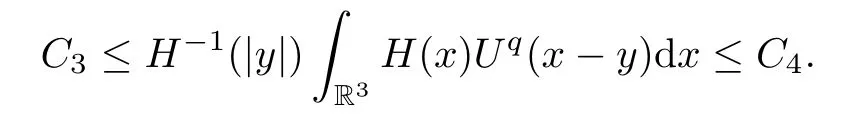
ProofThe first result is similar to the second one.Here we give the proof for the second.Letρbe a small constant.We have that

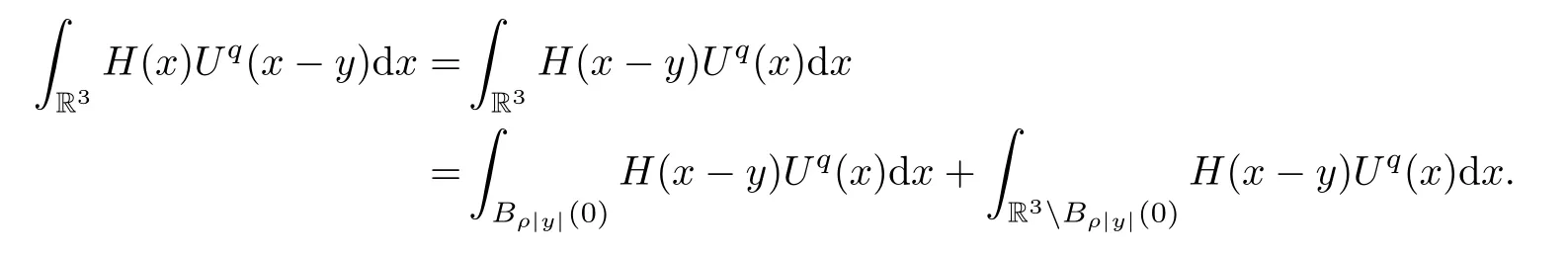
For |y| large enough,we have that

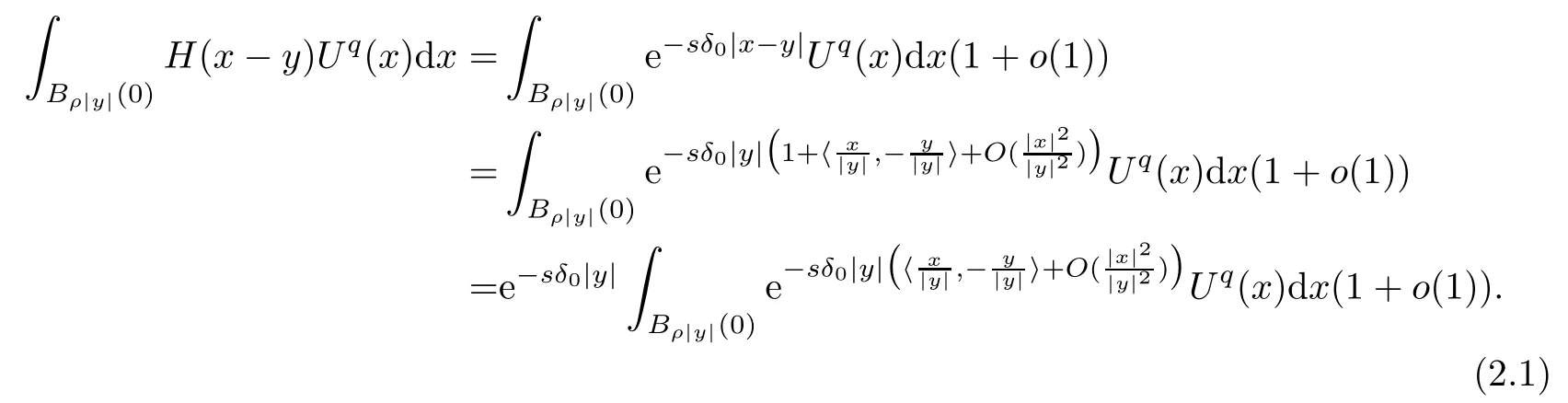
On the other hand,

Therefore,combining (2.1) with (2.2),the second result follows. □

In what follows,we use Lemma 2.1 to compute the energy functional.

Lemma 2.2Under the assumptions ofV(x),Q(x) andf(x),it holds that

satisfyC1≤B1(y),B2(y),B3(y) ≤C2for some constantsC2≥C1＞0.

ProofRecall that

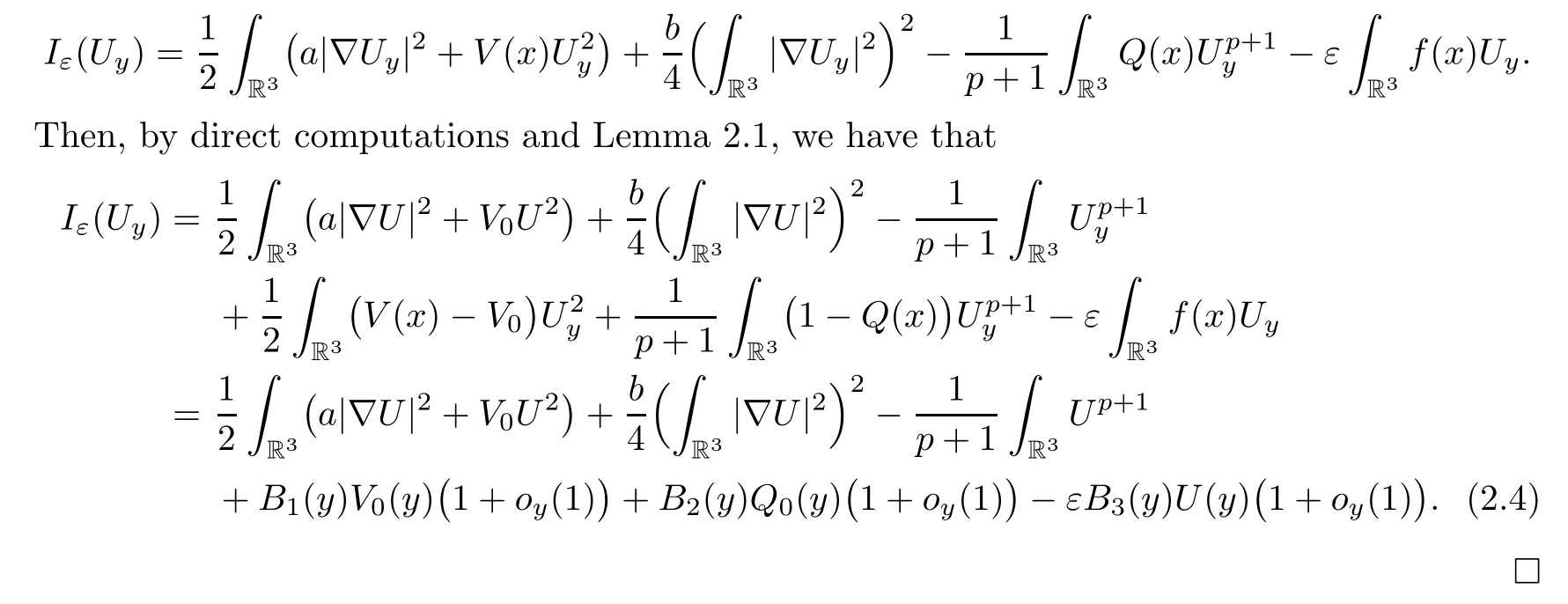
Finally,the estimates of the gradient for the energy functional will be given in the following.

Lemma 2.3Under our assumptions about functionsV(x),Q(x) andf(x),we have that

ProofBy direct computations,we have that

It is easy to verify that

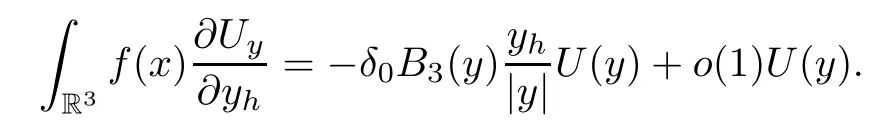
On the other hand,

Similarly,

Therefore,the result follows. □

3 Finite Dimensional Reduction and Proof of the Main Results

In this section,we intend to prove the main theorem by the Lyapunov-Schmidt reduction argument.

The constantδ ＞0 will be determined later.Ifs∈[s1,p+1),then

The variational functional corresponding to Problem 1.1 can be defined as follows:

By the expansion computation forJ(y,ω) atω=0,we have that

On the other hand,it is easy to check that the operator

is a bounded bilinear function inEy.Hence,by the Lax-Milgram theorem,there is a bounded linear operatorL,fromEytoEy,such that

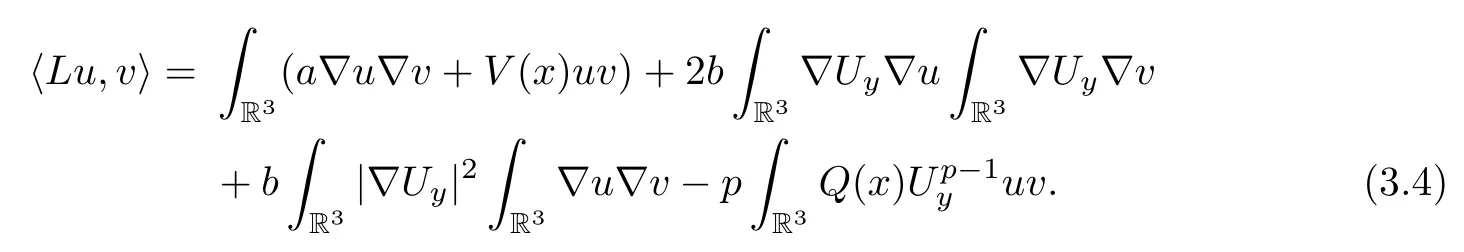
Next,we will prove that the operatorLis invertible inEy.

Lemma 3.1There is anε0＞0 such that,for any 0＜ε ＜ε0,we have that

whereρ ＞0 is a constant independent ofε.

ProofWe argue by contradiction.Assume that there existεn→0,|yn| →+∞andφn∈Eynwith ‖φn‖=1 such that

Thus,up to a subsequence,we may assume that

for someφ∈H1(R3).Next,we will prove that ?φ=0.

Note thatφn∈Eyn,so we have

which implies that

Therefore,we have that

Insertingφninto (3.6),then we have that

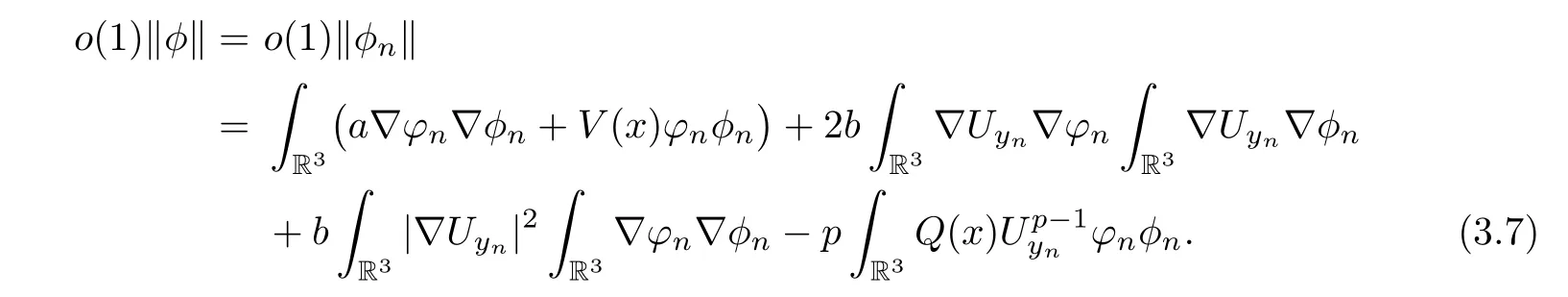
where the last equality follows from,for largeR ＞0,

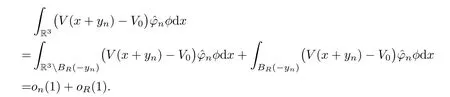
It is easy to obtain,by translation and weak convergence,that

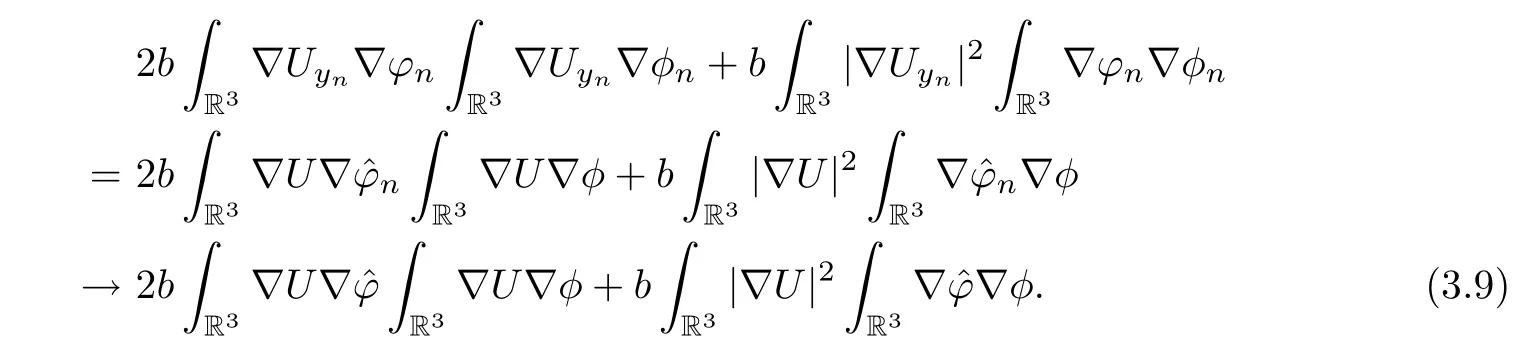
Similarly,it holds that

Hence,combining (3.7)–(3.9) with (3.10),asn→+∞,we have that

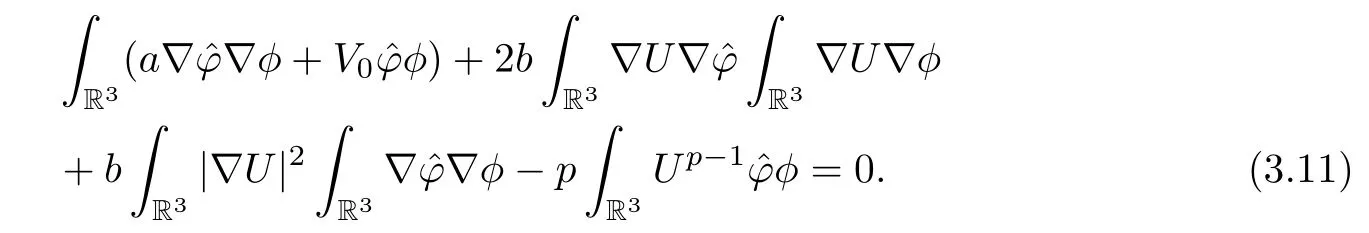
By Proposition 1.1 andφ∈,(3.11) holds for allφ∈H1(R3).By Proposition 1.1 again,we know that.Combining this with (3.5),we can deduce that=0.

On the other hand,we have that

which is a contradiction. □

Sincelis a continuous linear operator onEy,there exists a uniquel∈Eysuch that

Moreover,we have the following estimate of ‖l‖:

Lemma 3.2It holds that

ProofSinceUysatisfies (1.9),then,for anyφ∈H1(R3),we have that

By the conditions ofV(x) andQ(x),it can be deduced that

Moreover,by the conditions off,

Lemma 3.3We have that

ProofRecall that

By direct computation,we have that

Ifp ＞2,by using Hlder’s and Sobolev’s inequalities,we have that

Next,we will use Lemma 3.1 and Lemma 3.3 to find a suitableω∈Ey.

Proposition 3.4There existsε0＞0,such that,for allε∈(0,ε0),there exists aC1mapωεfromDεtoH1(R3) satisfyingωε∈Eyand

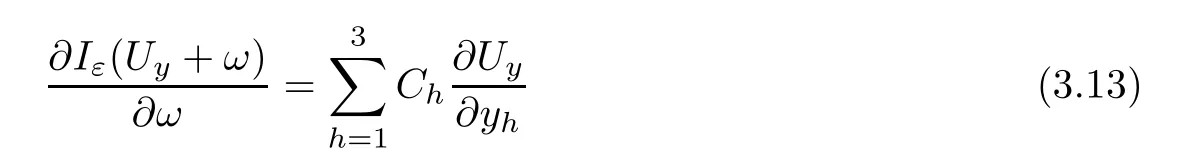
for suitable constantsCh,h=1,2,3.Moreover,

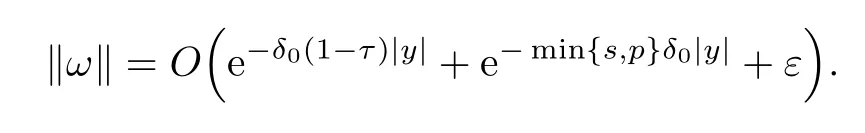
ProofThe problem of searchingωin (3.13) is equivalent to solving the problem

By Lemma 3.1,Lis invertible.Hence,(3.14) is rewritten as

whereδ ＞0 is small enough.

For anyω∈S,by Lemmas 3.1,3.2 and 3.3,we have that

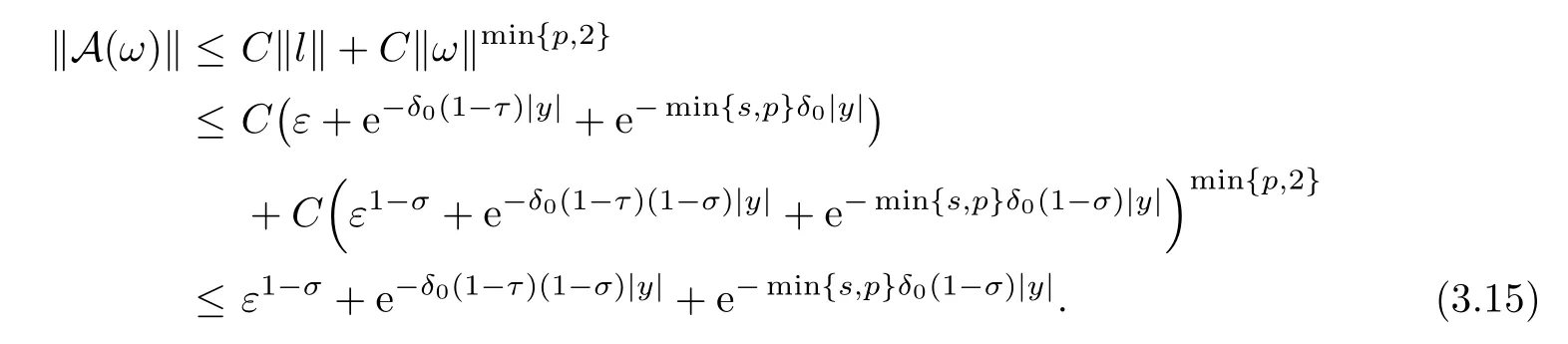
Hence,A is a map from S to S.On the other hand,for anyω1,ω2∈S,

which implies that A is a contraction map.Thus,there exists a unique solutionωε,y∈S such thatωε,ysatisfies (3.13). □

Now we are ready to prove our main theorem.Letωε=ωε,y.It follows from [18] that if Jεhas a critical point,thenUy+ωε,yis a solution of (1.1).Hence,to prove our main theorem,it suffices to prove that Jε(y)=Iε(Uy+ωε,y) has a critical point in Dε.

Proof of Theorem 1.2By direct computation,we have that

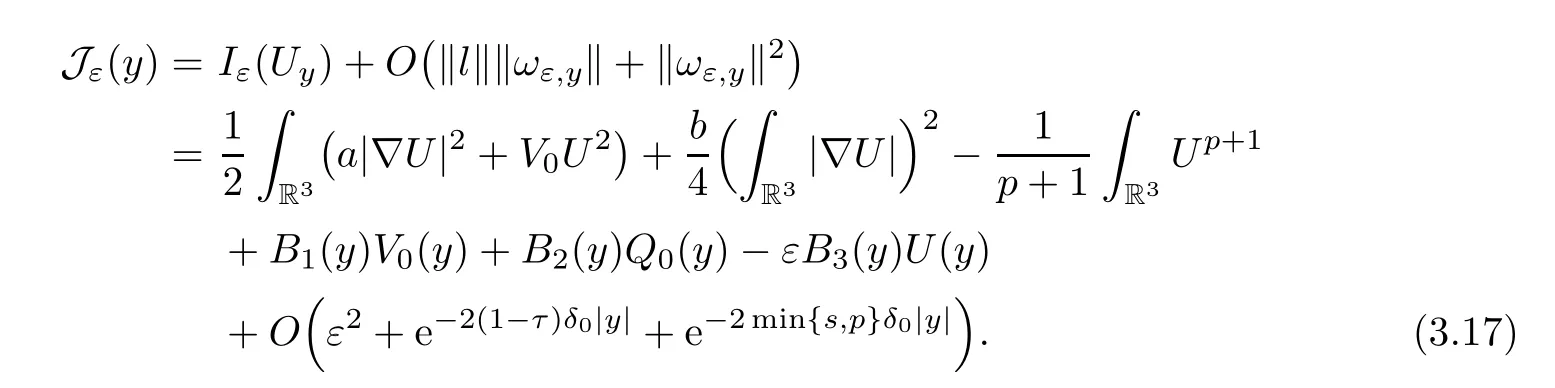
We only consider the cases∈(s1,p+1),since the others are similar.

Whens∈(s1,p+1),(3.17) can be rewritten as

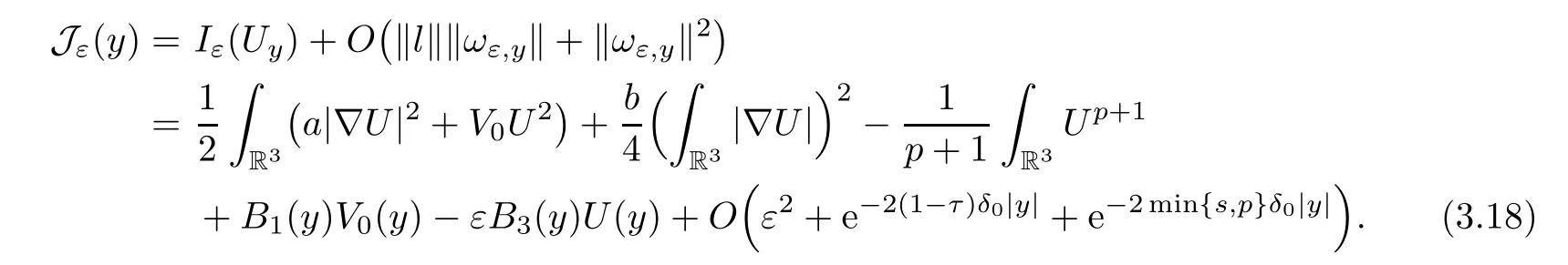
Through Lemma 2.3,we have that

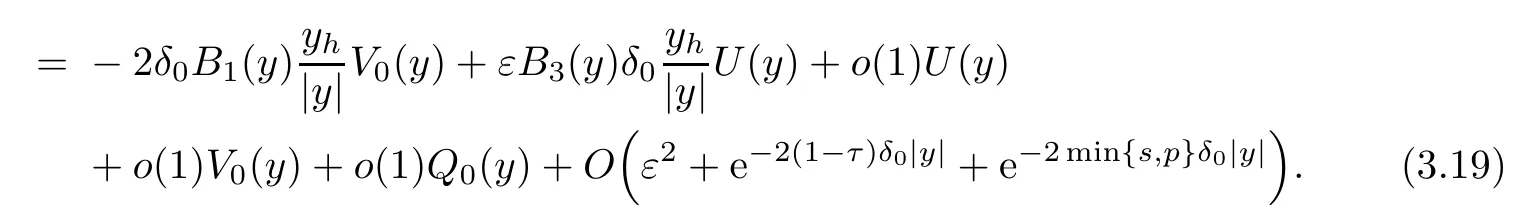
Next we will verify that

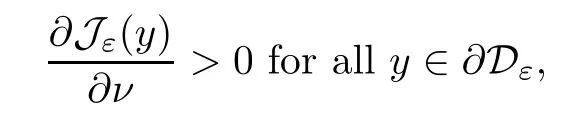
whereνis the outward unit normal of?Dεaty∈?Dε.

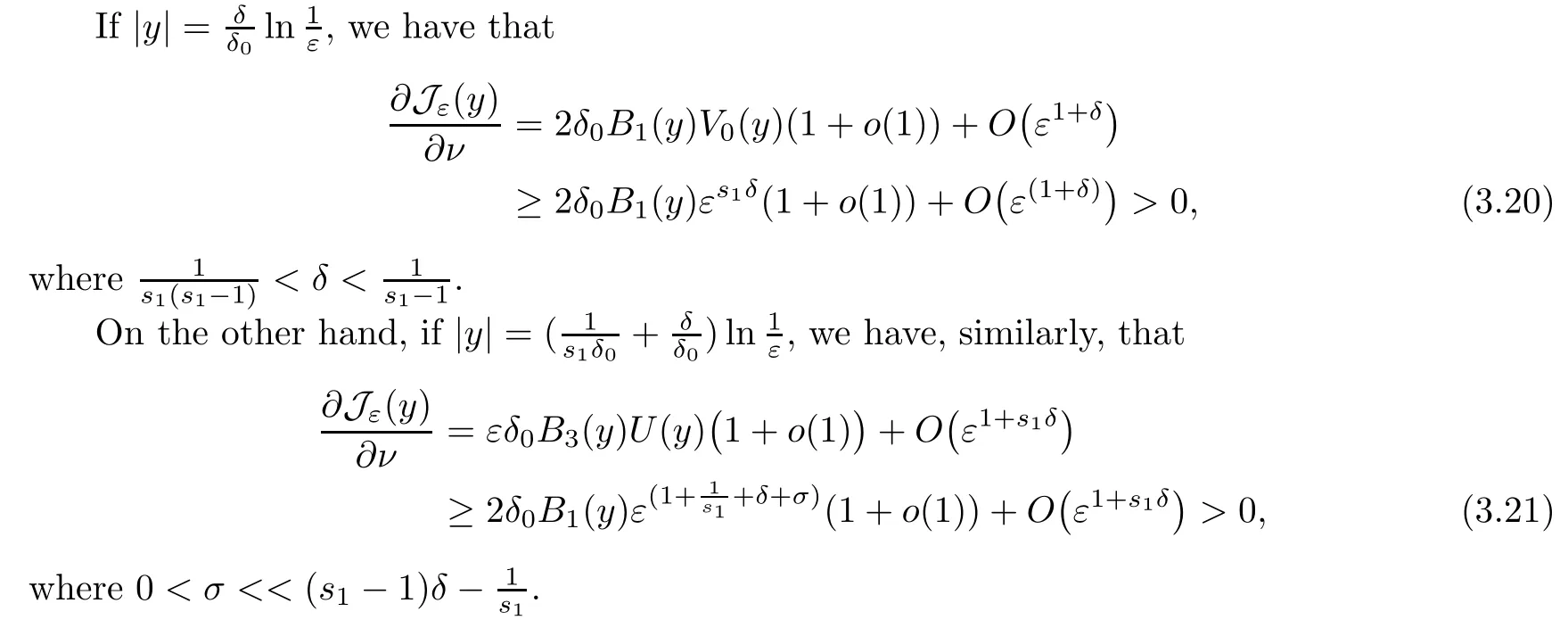
Combining (3.20) and (3.21) and employing the Lusternik-Schnirelman theory,we see that the number of the critical points of Jεin Dεis at leastCatDε=2.Consequently,the result is proved completely. □

AcknowledgementsThe authors are very grateful to Professor Shuangjie Peng for many helpful discussions and comments.