Thieu Huy NGUYEN Truong Xuan PHAM Thi Ngoc Ha VU The Sac LE3,

1.School of Applied Mathematics and Informatics,Hanoi University of Science and Technology Vien Toan ung dung va Tin hoc,Dai hoc Bach khoa Hanoi 1 Dai Co Viet,Hanoi,Vietnam

2.Department of Mathematics,Faculty of Information Technology,Thuyloi university Khoa Cong nghe Thong tin,Bo mon Toan,Dai hoc Thuy loi,175 Tay Son,Dong Da,Ha Noi,Viet Nam

3.Thuyloi University,Dai hoc Thuy Loi,175 Tay Son,Dong Da,Hanoi,Viet Nam

E-mail: huy.nguyenthieu@hust.edu.vn;xuanpt@tlu.edu.vn;ha.vuthingoc@hust.edu.vn;SacLT@tlu.edu.vn

Abstract In this paper we investigate the existence and stability of periodic solutions (on a half-line R+) and almost periodic solutions on the whole line time-axis R to the Boussinesq system on several classes of unbounded domains of Rn in the framework of interpolation spaces.For the linear Boussinesq system we combine the Lp -Lq-smoothing estimates and interpolation functors to prove the existence of bounded mild solutions.Then,we prove the existence of periodic solutions by invoking Massera’s principle.We also prove the existence of almost periodic solutions.Then we use the results of the linear Boussinesq system to establish the existence,uniqueness and stability of the small periodic and almost periodic solutions to the Boussinesq system using fixed point arguments and interpolation spaces.Our results cover and extend the previous ones obtained in [13,34,38].

Key words Boussinesq systems;periodic solutions;almost periodic solutions;unbounded domains;smoothing estimates;dual estimates;interpolation spaces;stability

1 Introduction and Preliminaries

1.1 Introduction

Let Ω be one of the following domains: the whole space Rn,the half space Rn+,a bounded domain inRnor an exterior domain Ω inRnwith a boundary?Ω of classC3forn≥3 or with boundary?Ω of classC2+μ,(μ ＞0) forn≥4.We consider the following Boussinesq system for convection-diffusion processes in Ω and on the half-line time axis R+:

where divfrepresents the reference temperature for a vector fieldf,divFrepresents the external force for a given second order tensor fieldFandgrepresents the acceleration of gravity.Usually,in models for geophysical fluids,(whereGis a constant).However,in the present paper,we will consider the more general form ofgand suppose thatgsatisfies the Assumption 2.1 below.Furthermore,the unknowns areu(x,t) ∈Rn,p(x,t) ∈R andθ(x,t) ∈R representing the velocity field,the pressure and the temperature of the fluid at point (x,t) ∈Ω × R,respectively.

The Boussinesq system of hydrodynamics equations arises from zero order approximation to the coupling between the Navier-Stokes equations and the thermodynamic equation modeling the fluid movement by the natural convection (see [26]).Historically,the existence of mild solutions to the Boussinesq system has been studied in the works [1,2,9,11,12,14,24].The asymptotic behaviors of the solutions such as decay and stability have been studied in[1,6,10,13,23–25,32,33].The existence of time periodic solutions to Boussinesq system(1.1) in bounded and exterior domains has been established in [31] and [34,38],respectively.The authors in [34,38] considered the Boussinesq system (1.1) in the product of weak-Lnspaces,i.e.,,where Ω ?Rnis an exterior domain.They used the interpolation spaces and Kato’s iteration scheme to construct mild periodic solutions to (1.1) under certain conditions on the boundedness of the temperature term and of the external force in suitable interpolation spaces.

In the present paper,we first consider the system (1.1) on only a half-line time-axis R+and prove the existence,uniqueness and stability of a periodic solution to (1.1) in this case.Usually,the evolution of a physical quantity may be studied only from certain initial time onward.Therefore,it seems more natural to consider the Boussinesq system (1.1) on only a half-line time-axis R+.When considering (1.1) on R+,we face a difficulty that the system (1.1)is defined only on a half-line time-axis R+.Therefore,we have no information of the system on the other half-line R-.Hence,we can not use the notions of mild solutions in the sense of Kozono and Nakao [30],nor the weak mild solutions in the sense of Yamazaki [35,36] or Nakao [34]since all such notions of solutions require that the system is defined on the whole line time-axis R.Thus,in our situation when the system is defined only on a half-line,we propose another approach to the problem of the existence and stability of periodic solutions to Boussinesq system (1.1) on exterior domains and on half-line R+by exploiting the method posed in [20].Namely,we combine theLp-Lqsmoothness,duality estimates and interpolation functors to prove the existence of a bounded mild solution for the linear Boussinesq system.Then we invoke Massera’s principle to obtain the existence of a periodic solution using the boundedness of solutions.More precisely,using a sequence of Cesàro sums and Banach-Alaoglu’s theorem,we construct an initial datum from which emanates a mild periodic solution for the inhomogeneous linear Boussinesq system (see details in Theorem 2.3 in Section 2).This method allows us to prove the existence of a unique periodic solution to linear Boussinesq system when the system is defined only on a half-line time-axis R+.The existence and stability of the periodic solutions of the Boussinesq system will be established by fixed-point arguments and the duality estimates between the interpolation spaces (see Theorem 3.1 in Section 3).

On the other hand,in case the system (1.1) is defined on the whole line time-axis,we will go farther than the previously obtained results by establishing the existence and stability of the almost periodic solutions to the Boussinesq system (1.1).In our best knowledge,up to now there has been no results on the almost periodic mild solutions to the Boussinesq system (1.1).We try to fill in this gap by extending the method in [18,22].Namely,we will consider the Boussinesq system for allt∈R and use the notion of mild solutions considered by Kozono and Nakao in [30].Then,we use interpolation functors to prove the existence and boundedness (in time) of such mild solutions.The boundedness of solutions allows us to construct a solution operator preserving the almost periodicity.Therefore,we can prove the existence of the almost periodic solution for the linear Boussinesq system under each almost periodic external force.The existence and stability of the small almost periodic solutions to the Boussinesq system(1.1) will be done in a similar way as the case of periodic solutions.Our main result on almost periodic solutions to Boussinesq system is contained in Theorem 4.3.

1.2 Preliminaries

In what follows,we recall some notations and preparatory results and for latter use.

First,since divu=0 and using the identity

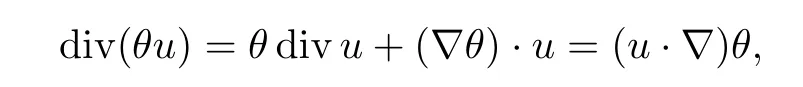
the Boussinesq system (1.1) can be rewritten as

We recall the following standard and homogeneous Sobolev spaces:f

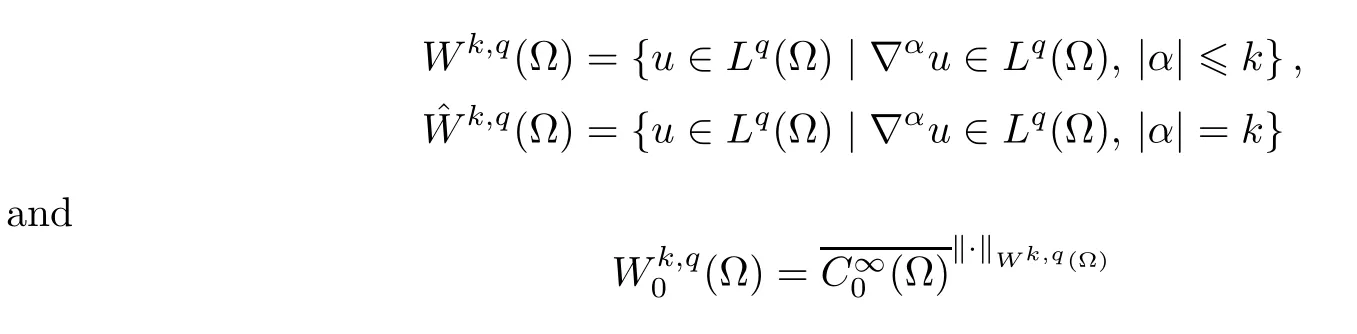
or 1＜q ＜∞,k∈N.

Next,we denote byB:=Bq=-Δ the Laplace operator onLq,1＜q ＜∞;with domainWe recall that the operator -Bgenerates a bounded analytic semigroupon eachLq(Ω) (see,e.g.,[7,19]).

In order to define the Stokes operator,we need the Helmholtz decomposition of the spaceLq(Ω) as

We recall the following results onLp-Lqestimates for Stokes semigroupe-tAand heat semigroupe-tB(see [8,Theorem 3.10],[13,Remark 5] and [30,Lemma 2.1]):

Proposition 1.1Let Ω be a domain in Rn.Fora∈(Ω) with 1＜p ＜∞andt ＞0:

i) [13,Remark 5]: If Ω is a bounded domain in Rn,n≥3 withC2-boundary?Ω,then the following inequalities hold:

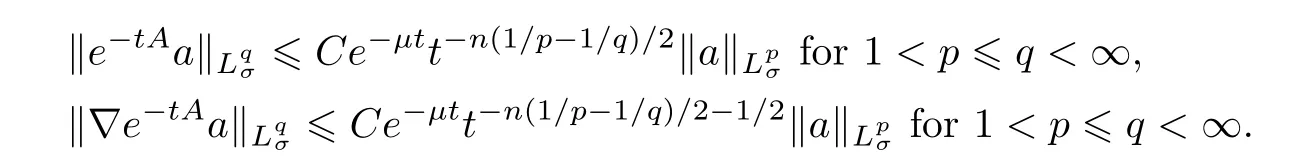
ii) [30,Lemma 2.1]: If Ω is the whole spaceRnor the half-space Rn+,n≥3,then the following inequalities hold:

iii) [8,Theorem 3.10] and [30,Lemma 2.1]: If Ω is an exterior domain in Rn,n≥3,withC3-boundary?Ω or an exterior domain in Rn,n≥4 withC2+μ-boundary?Ω (μ ＞0),then the following inequalities hold:

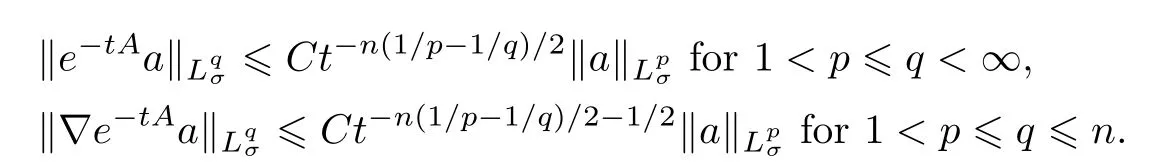
The same estimates hold forLq-norm of the semigroup ‖e-tBf‖Lq,wheref∈Lp(Ω).

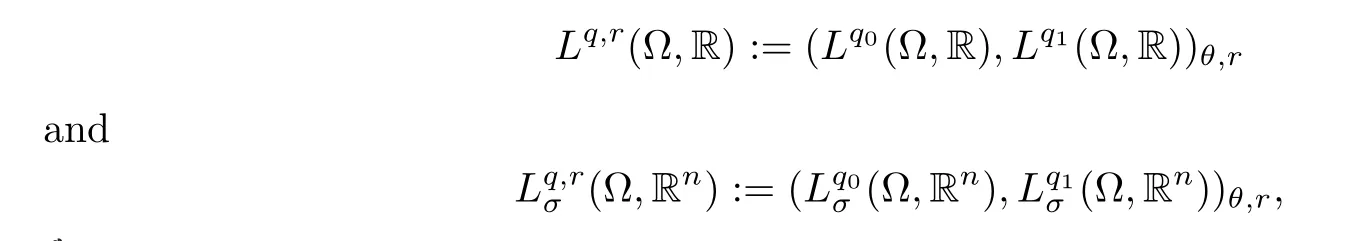
To exploit these estimates to the framework of interpolation spaces,we need the Lorentz spaces and solenoidal Lorentz spaces defined as respectively,where 1＜q0＜q ＜q1＜∞,1 ≤r≤∞andThen,by interpolation theorem,are extended to the bounded analytic semigroups on the spaceLr,q(Ω) and,respectively.

For simplicity in the presentation we denote

The dual space ofLq,r(Ω) (resp.isLq*,r*(Ω) (resp.,whereandfor 1 ≤r;q ＜1.Specially,we meanr*=∞andq*=∞,whenr=1 andq=1,respectively.Moreover,we recall the following weak Hlder inequality.

Proposition 1.2Let 1＜p0,p1＜∞and 1 ≤q0,q1≤∞,q=min {q0,q1} andp ＞1 satisfyThen,for allf∈Lp0,q0andg∈Lp1,q1we have thatfg∈Lp,qand there exists a constantC ＞0 such that

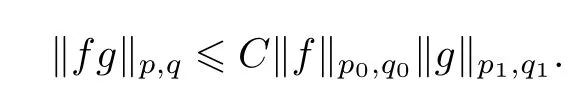
Using Proposition 1.1 we obtain theLq,r-Lp,restimates fore-tA(and similarly fore-tB)in the following proposition.

Proposition 1.3Fora∈(Ω) with 1＜p ＜∞,1 ≤r≤∞andt ＞0:

i) If Ω is a bounded domain in Rn,n≥3 withC2-boundary?Ω,then the following inequalities hold:

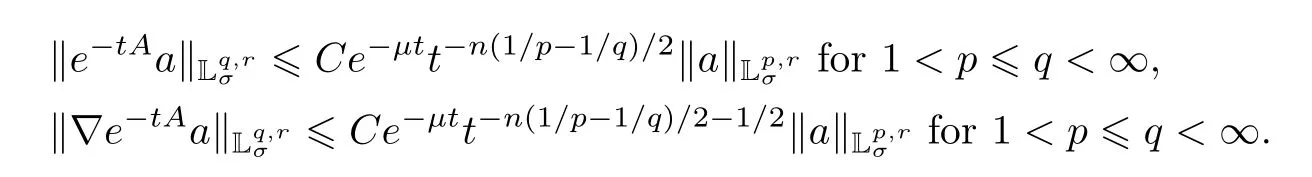
ii) If Ω is the whole space Rnor the half-space Rn+,n≥3,then the following inequalities hold:

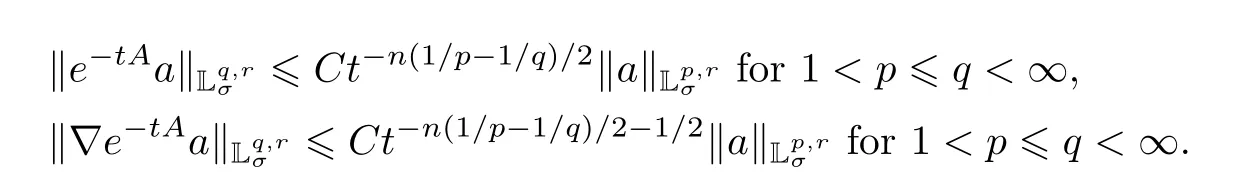
iii) If Ω is an exterior domain in Rn,n≥3,withC3-boundary?Ω or an exterior domain in Rn,n≥4 withC2+μ-boundary?Ω,then the following inequalities hold:

The same estimates hold for ‖e-tBb‖Lq,rand ‖?e-tBb‖Lq,r,whereb∈Lp,r(Ω).

Applying the Helmholtz projection P to the system (1.2) we obtain the following system

We now rewrite the above system in the form of a general evolution equation in the Cartesian product space.To this purpose,we set the operatoracting on the Cartesian product spacewith the domainD(A)×D(B).Then,equation(1.3) is rewritten in the operator matrix form as

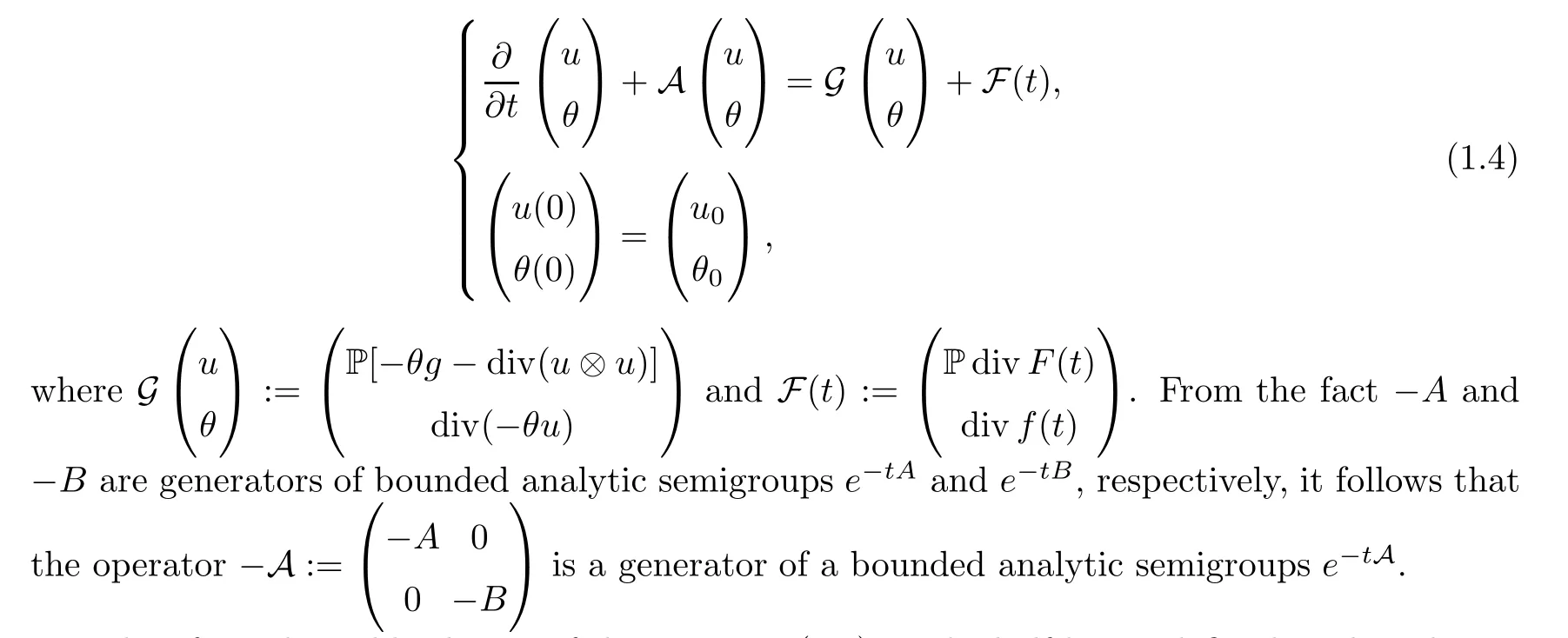
Therefore,the mild solution of the equation (1.4) on the half-line is defined as the solution of the integral equation

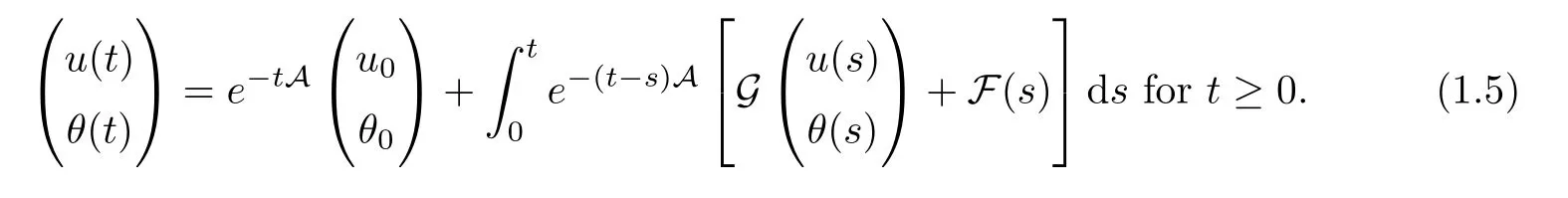
2 Bounded and Periodic Solution to the Linear Boussinesq System on a Half-line

We consider the following linear equation

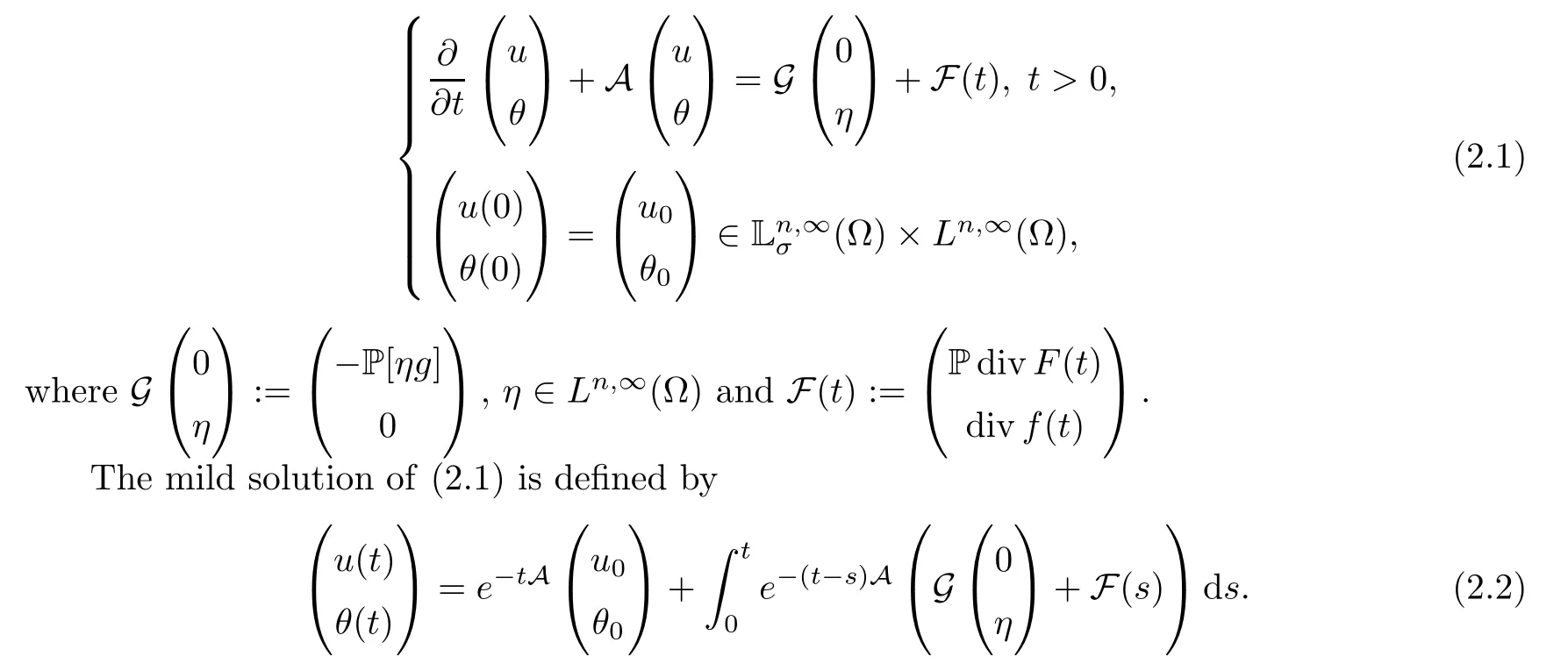
We need the space of bounded and continuous functions with values in a BanachXdefined as

to emphasize that we are working with weakLp-spaces.Moreover,for the Lorentz spaceX,we denote the norm inXby ‖f‖p,q:=‖f‖XforX=Lp,q(Ω),and ‖f‖p,w:=‖f‖XforX=Lp,∞(Ω).Note that the letter ‘w’ in the sub-indices means ‘weak’.

Furthermore,we denote the norm in,Ln,∞(Ω)) by

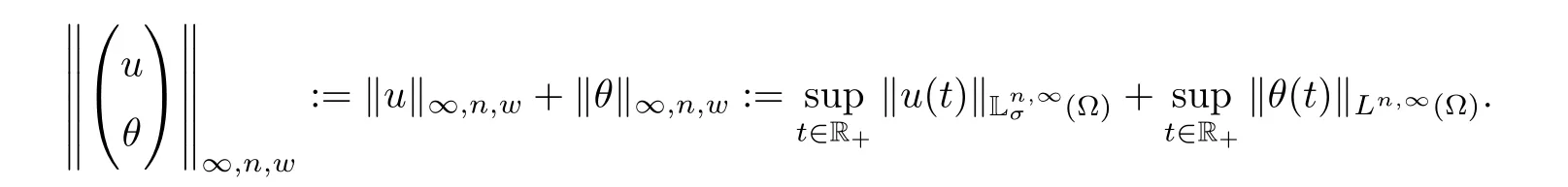
Assumption 2.1Assume that the functiongforn ＞3.Moreover,forn=3 we assume that there exist constants 0＜b ＜1＜a ＜such that

We would like to note that the above assumption is necessary to establish the boundedness(in time) of the mild solution to the linear equation (2.1) and also semi-linear equation (1.4).The existence of the bounded mild solution of (2.1) was proved in some previous works.In particular,Ferreira et.al.[13,Lemma 3.4 and Theorem 2.4] proved the existence of solutions inunder the condition thatIn the recent work,Nakao [34,Theorem 3.1] proved the existence of solutions inL2,∞(Ω) ∩L4,∞(Ω)) withg∈,where Ω is an exterior domain in R3.

We note also that,in casen=3,Assumption 2.1 does not cover the physical fieldg=since the functionfor 0＜b ＜1＜a.

For the sake of completeness,we state and prove the existence of solutions under Assumption 2.1 in the following theorem.

Theorem 2.2Letn≥3.Suppose that the external forcesand thatgsatisfies Assumption 2.1.Then,the problem (2.1) has one and only one bounded mild solution (u,θ) ∈Cb(R+,Ln,∞(Ω)) given by the formula (2.2) with (u(0),θ(0))=(u0,θ0) satisfying

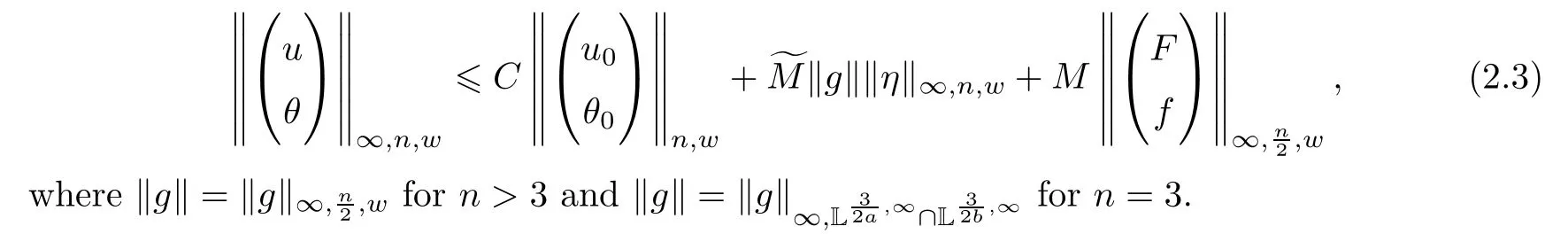
ProofUsing interpolation techniques as in [20–22,36]) it can be proved that for eachandn≥3 we have

As a consequence of the inequalities (2.4) and (2.5) we obtain that forn≥3,

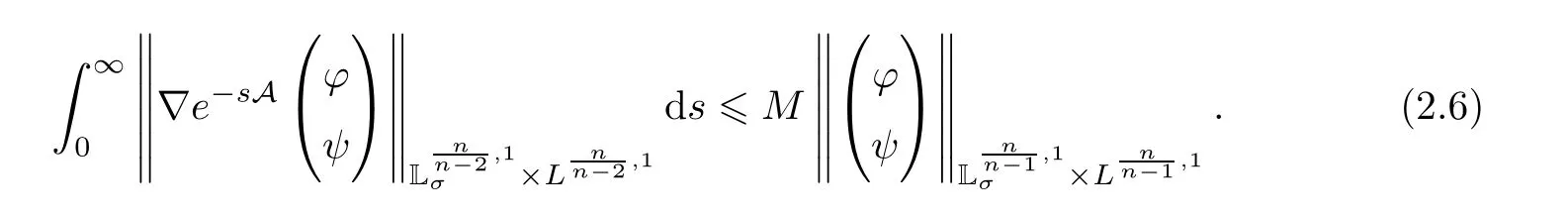
Consideringn ＞3,by the same way as above,we also have that

We now use (2.6) and (2.7) to estimate the norm ‖(u,θ)‖∞,n,w.To do this,denote by〈·,·〉 the dual pair between.For each (φ,ψ) ∈by using the weak Hlder inequality in Proposition 1.2 i),(2.6) and(2.7) we estimate that

Therefore,the inequality (2.3) holds.

Now we considern=3.There exists a constantCsuch that (see [34,Lemma 4.2]):

Therefore,by the interpolation theorem we have (see [3,Theorem 5.3.1]):

The last inequality is due to (2.6).

Using the above inequality we can estimate the normby the same way as done in (2.8) and get (2.3) with.Our proof is completed. □

Theorem 2.3Letn≥3.Given the external forcesF∈,f∈andgsatisfying Assumption 2.1.Suppose that these external forces areT-periodic with the same periodT.Then,there exists a unique mildT-periodic solutionto the problem (2.1).Moreover,satisfies

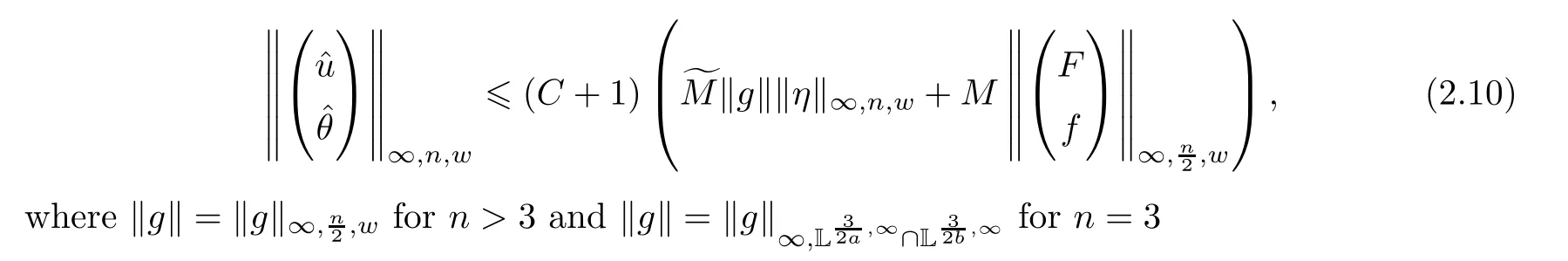
ProofWe develop the method in [20,Thm.2.2] to establish the existence and uniqueness of the periodic mild solution of the equation (2.1).

is the unique mild solution of (2.1) with

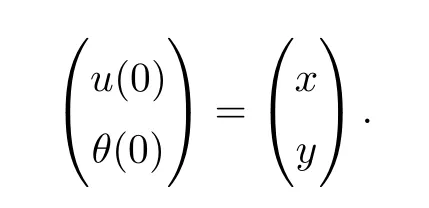
Note that using the formula (2.2) of the solutions we see that

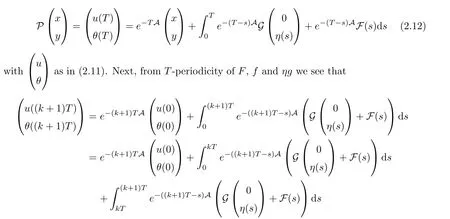
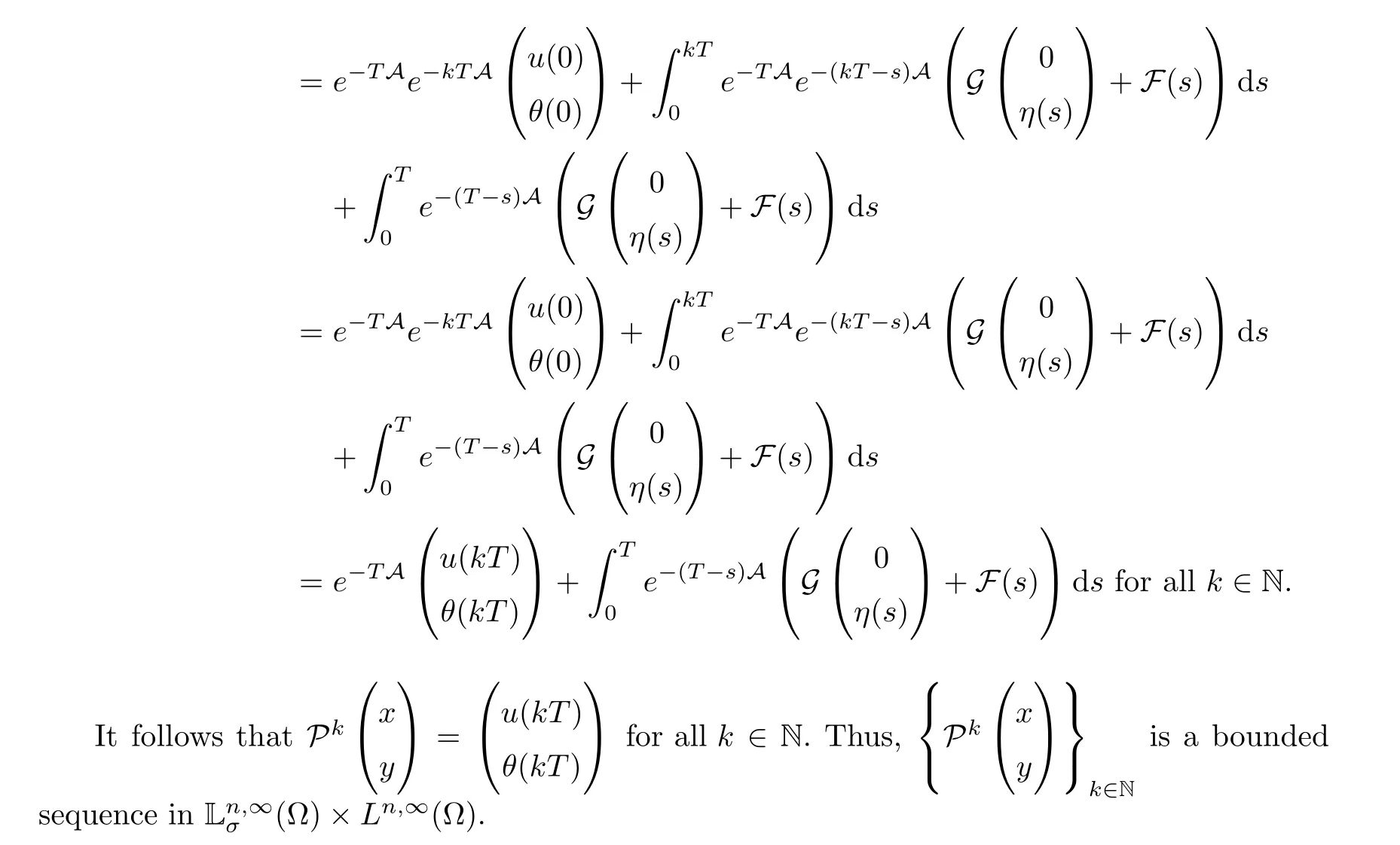
Next,as usual in ergodic theory,for eachn∈N we define the Cesàro sum Pnby

By simple computations using formula (2.13) we obtain

This limit,together with (2.16),leads us to

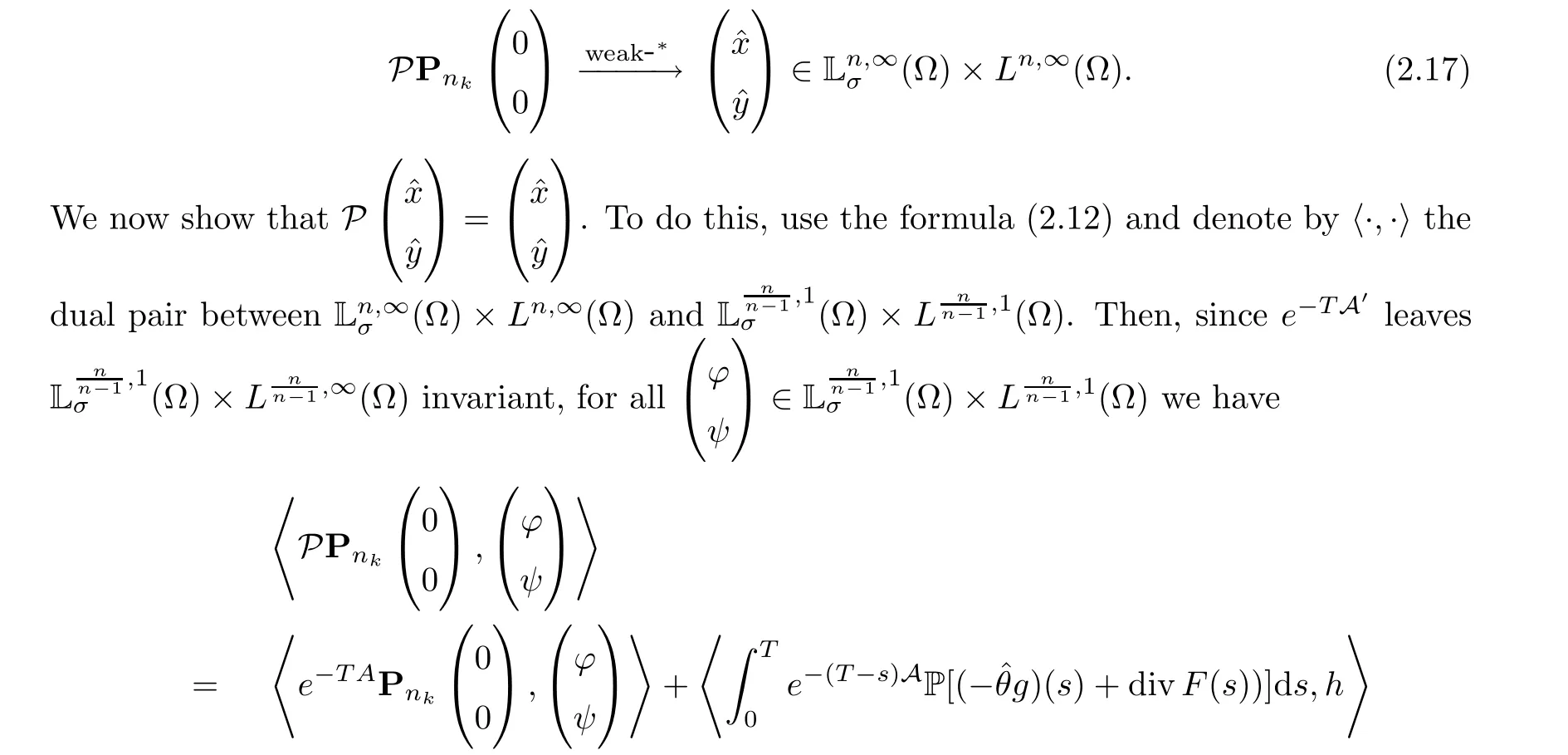
It now follows from (2.17) and (2.19) that

This fact,together with the periodicity ofvandη,implies thatfor allt≥0.This yieldsThe uniqueness holds. □

3 Existence and Stability of Periodic Solutions to the Boussinesq System

We now investigate the existence,uniqueness and stability of periodic mild solutions to the Boussinesq system (1.4).The mild solution (u(t),θ(t)) to (1.4) with the initial data(u(0),θ(0))=(u0,θ0) is defined as follows

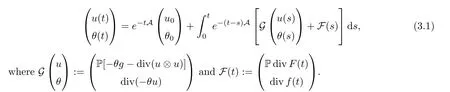
The existence of the periodic mild solution of the semi-linear equation (1.4) was previously proved in some works.Precisely,Villamizar-Roa et.al.[38,Theorem 1] proved the existence of such a solution in the spacewithg∈Cb(R+,La,∞(Ω) ∩Lb,∞(Ω))and Nakao has proved the existence in the spacewithwhere Ω is an exterior domain in R3in the recent work [34,Theorem 3.1].The stability of mild solutions was established in [13,Theorem 2.3 and Theorem 2.4]under some decaying condition ongin.Here,we will give another proof for the existence and stability of the periodic mild solution by using Theorem 2.3 and Assumption 2.1.The main theorem of this section reads as follows.

Theorem 3.1Letn≥3.Given the external forces,f∈andgsatisfying Assumption 2.1.Suppose thatF,f,andgareT-periodic with respect totwith the same periodT.Then,the following assertions hold.

for allt ＞0,wherer ＞nandCis a positive constant.

Proof(I) We prove this assertion by using the existence of periodic mild solutions to the linear equation and the estimates (2.10) obtained in Theorem 2.3 in combination with fixed-point arguments.Putting

We define the transformation Φ as follows: For each (v,η) ∈Bρ×Bρwe set Φ(v,η)=(u,θ)whereis the uniqueT-periodic solution to the following integral equation

Moreover,for (v1,η1) and (v2,η2) in Bρ×Bρby applying again the inequality (2.10) with

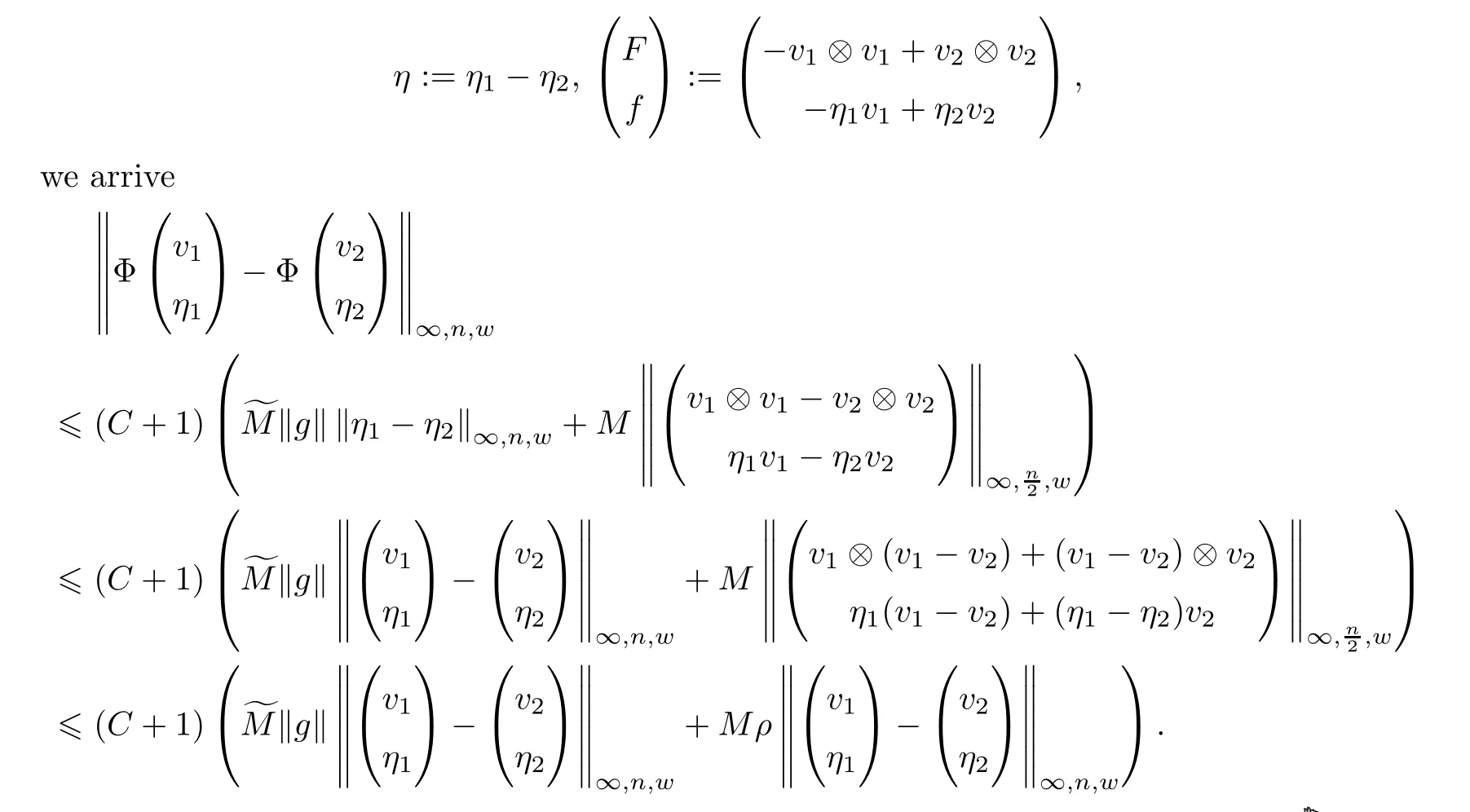
Hence,ifρa(bǔ)nd ‖g‖ are sufficiently small the map Φ is a contraction.Then,there exists a unique fixed pointof Φ.By definition of Φ,the functionis the uniqueT-periodic mild solution to the equation (1.4) and the assertion (I) holds.

(II) Using the interpolation techniques it can be proven that (see [20–22,36])

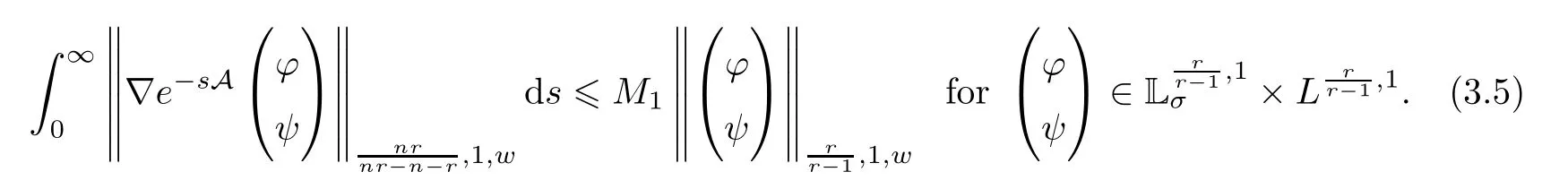
Moreover,Sincen≥3,we have that,hence.This leads tonr-n-2r ＞0.Therefore,again the interpolation techniques yields that

Indeed,for (v,η) ∈M we consider the mapping Φ defined formally by

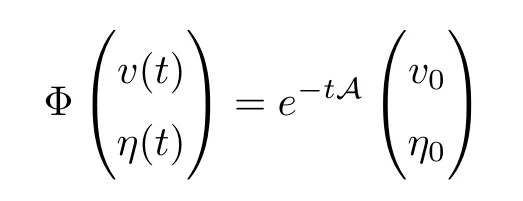
By estimates i) in Proposition 1.3 for semigroups (e-tA)t≥0and (e-tB)t≥0we obtain that

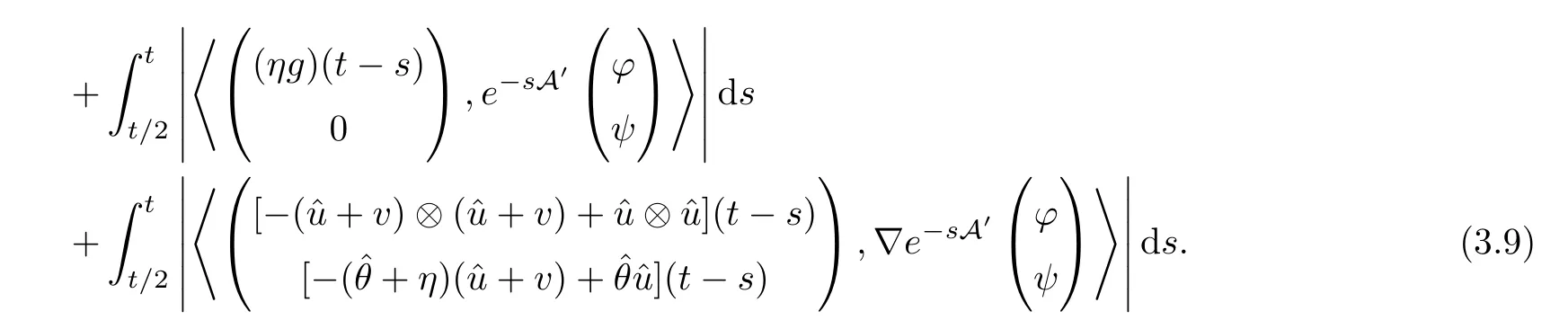
We then estimate the three integrals on the last line of (3.9).Forn ＞3,the first integral is estimated as follows:

Forn=3 we have (see [3,Theorem 5.3.1]):

Therefore,inequality (3.10) becomes

We next estimate the two last integrals in (3.9).Forn ＞3 we have

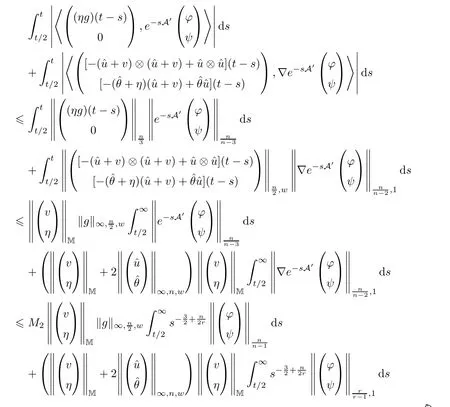
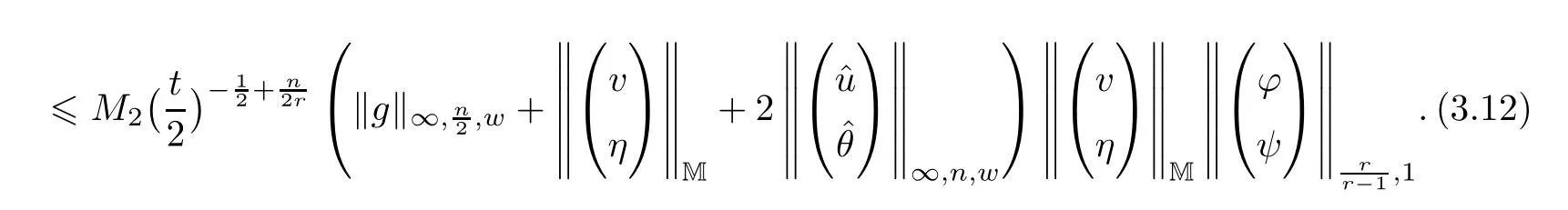
Forn=3,by the same way as in the proof of Theorem 2.2 we can estimate that

Combining now (3.9),(3.10),(3.11),(3.12) and (3.13) we obtain that:

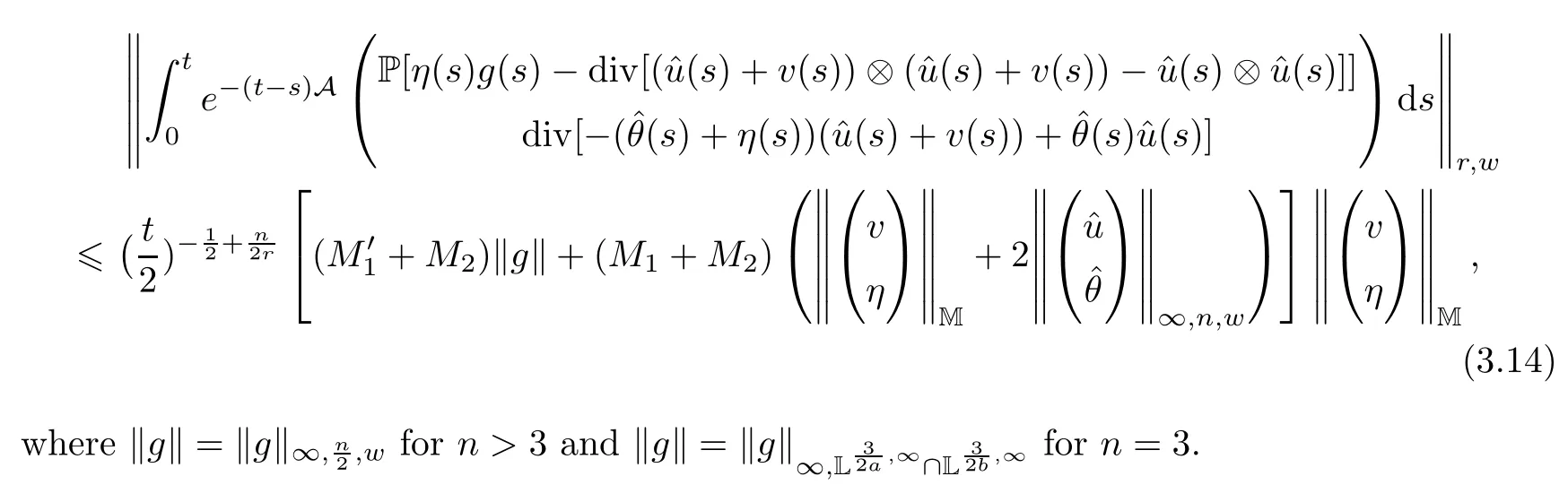
In view of the inequalities (3.8) and (3.14),we have that

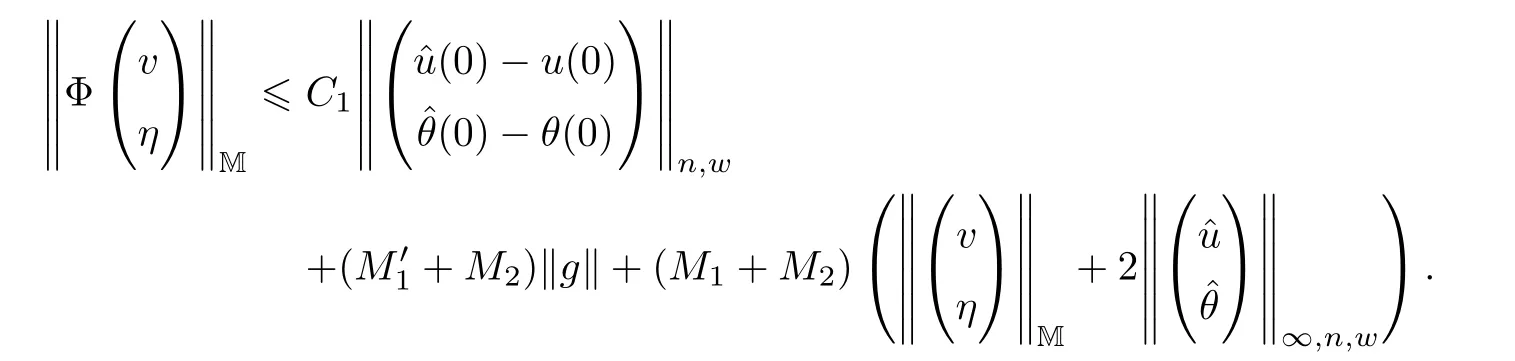
Similar calculations yield

Remark 3.2In the cases of bounded domains,since the semigroupe-tAis exponentially stable as in Proposition 1.3 i),the polynomial stability of the solution (?u,?θ) obtained in Theorem 3.1 can be improved to become exponential stability: Concretely,under the same conditions in Theorem 3.1,if the domain Ω is bounded,then we have that

4 Almost Periodic Solutions to Boussinesq Systems on the Whole Line

This Section we consider the Boussinesq system in on the whole line time-axis of the form

The corresponding linear system of (4.1) is

We will show the existence and uniqueness of the almost periodic mild solutions to equations(4.3) and (4.1).To this purpose,we first recall the notion of almost periodic functions in the following definition.

Definition 4.1A functionh∈Cb(R,X) is called almost periodic if for each∈＞0,there existsl∈＞0 such that every interval of lengthl∈contains at least a numberTwith the following property

We denoteAP(R,X) :={h: R →X|his almost periodic} which is a Banach space endowed with the norm

To establish the boundedness of mild solutions of equations (4.1) and (4.3) we need the following assumptions forgon the whole line time-axis.

Assumption 4.2Assume that the functionforn ＞3.Moreover,forn=3 we assume that there exist constants 0＜b ＜1＜a ＜such that

We now come to our main result in this section.

Theorem 4.3Letn≥3.Suppose that Assumption 4.2 holds and that the external forcesF,fand functionsη,gare given such that the functiont(F(t),f(t),g(t),η(t)) belongs toThen the following assertions hold.

(I) Problem (4.3) has one and only one almost periodic solution (?u,?θ(t)).Moreover,forn ＞3 we have

for allt ＞0 andr ＞n.Moreover,in the cases of bounded domains we have the following exponential stability

Therefore,the inequality (4.6) holds.

Now we considern=3.By the same way as in the proof of Theorem 2.2 we have that

The inequality (4.6) allows us to define the solution operator

We now prove that the operatorSpreserves the almost periodic property,i.e.,if (F,f) is almost periodic,so isS(F,f).Indeed,we can reformulateS(F,f) in the form

There areLδ＞0,such that for eacha∈R,we can choose aT∈[a,a+Lδ] with

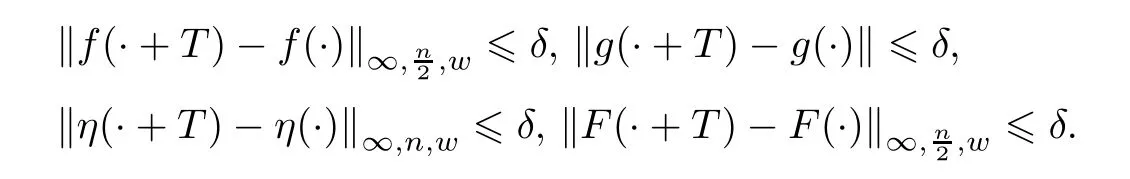
Therefore,we have that

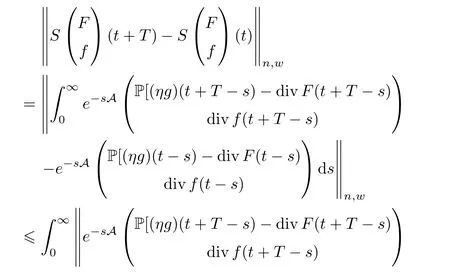
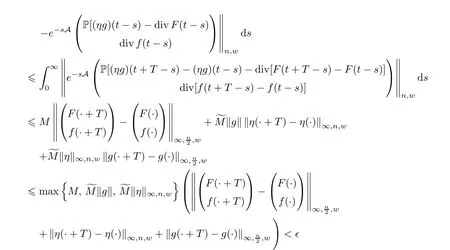
for allt∈R.It follows thatSpreserves the almost periodicity of the functionh=(F,f).Therefore,for the almost periodic functiont(F(t),f(t),η(t),g(t)) we have that the mild solutionis also almost periodic.

(II) The proof of Assertion (II) can be done in a same way as done in Theorem 3.1 (I) by using the inequality (4.6).

(III) Observe that fort ＞0 we have

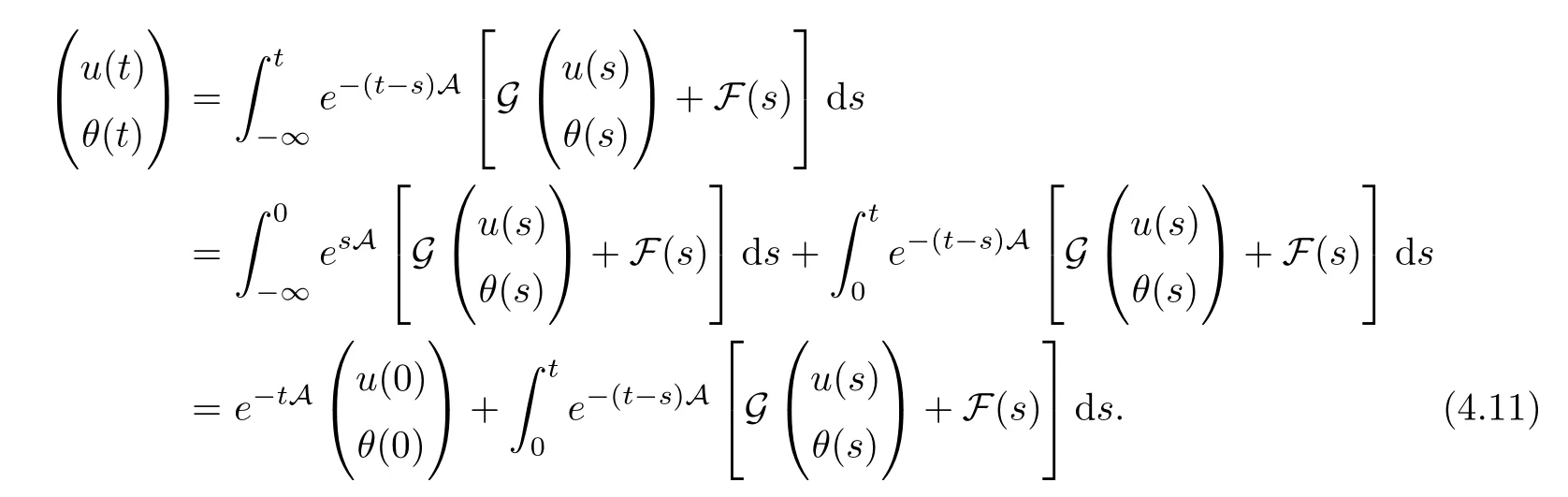
Using formula (4.11),the proof of Assertion (III) can be done by a similar way as in Assertion(II) of Theorem 3.1. □

We would like to note that from the above proof it follows that the solution operatorSdefined as in (4.10) satisfies

Therefore,ifF,f,η,gareT-periodic then clearly the mild solutionisT-periodic.Thus we have the following theorem on the existence of periodic solutions to the Boussinesq system.

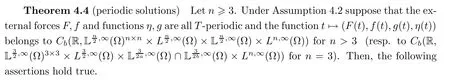
(I) The linear problem (4.3) has one and only oneT-periodic solution (?u,?θ).Moreover,forn≥3 we have

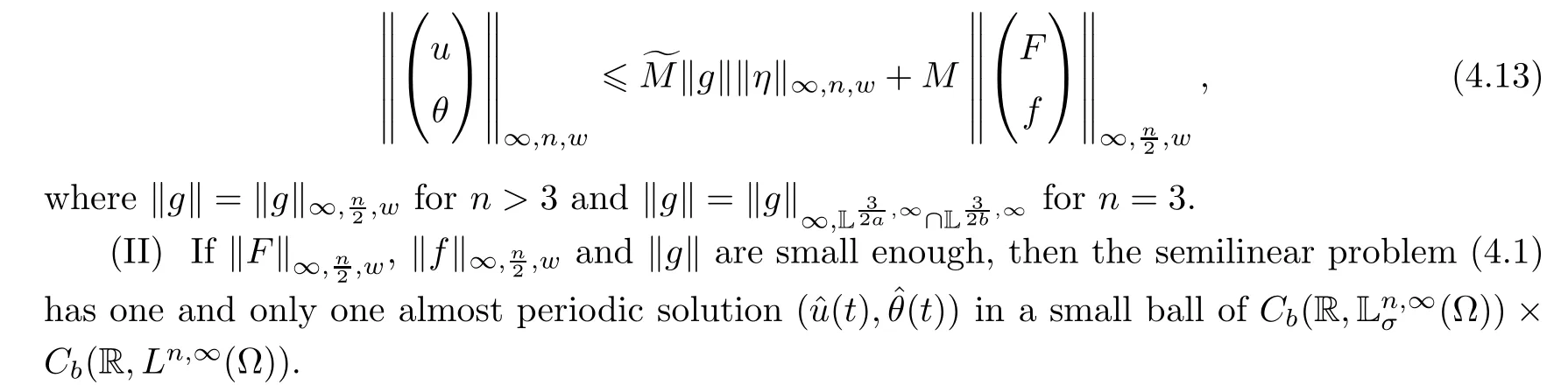
(III) The periodic mild solutionof the equation (4.1) is stable in the sense of Assertion (III) in Theorem 4.3.

ProofAssertion (I) follows from estimate (4.12) of the solution operatorS.Assertions(II),(III) can be proved in a same way as in the corresponding proofs of Theorem 4.3 ((II) and(III),respectively). □