用換元法探究一類最值問題的解法與推廣
2023-04-17 09:01:22程元慧安徽省績溪中學(xué)245300
中學(xué)數(shù)學(xué)月刊 2023年4期
程元慧 (安徽省績溪中學(xué) 245300)
對某種復(fù)雜的最值問題,如果從題目內(nèi)部結(jié)構(gòu)出發(fā),通過等價變形,找到變量相等的條件后作換元處理,就能使均值不等式的運(yùn)用有了用武之地.
例1(《數(shù)學(xué)通報(bào)》2012年第9期數(shù)學(xué)問題2080題)正數(shù)a,b,c滿足a+2b+3c≤abc,求5a+22b+c的最小值.
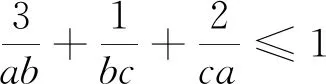
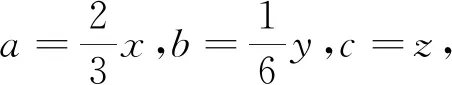
例2(2008年全國高中數(shù)學(xué)聯(lián)賽吉林省預(yù)賽試題)已知正數(shù)a,b,c滿足2a+4b+7c≤2abc,求a+b+c的最小值.
按照例1的方法加以分析,同樣可以得到下面的簡單解法.
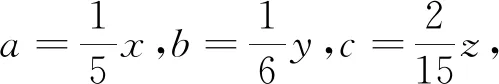
對上述兩道例題的解法進(jìn)一步分析,可將它們作如下推廣:
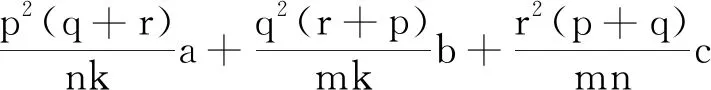
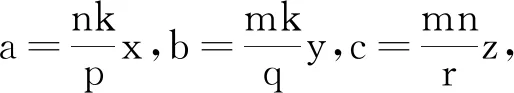
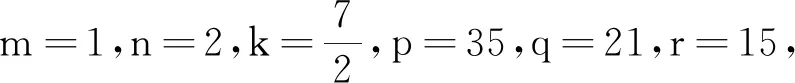
經(jīng)典的數(shù)學(xué)問題總是存在著變的學(xué)問,或已知條件在變,或所求目標(biāo)在變,但是不論怎么變,條件和目標(biāo)之間總隱含著某種神秘的關(guān)系,只要在解題時用心觀察,仔細(xì)思考,就會讓這種關(guān)系浮出水面,從而打開解題的綠色通道.
猜你喜歡
中等數(shù)學(xué)(2021年7期)2021-11-22 07:26:04
漢語世界(The World of Chinese)(2021年2期)2021-04-22 05:39:23
漢語世界(2021年2期)2021-04-13 02:38:00
中等數(shù)學(xué)(2020年3期)2020-08-24 07:59:24
中學(xué)生數(shù)理化·七年級數(shù)學(xué)人教版(2019年9期)2019-11-25 07:34:34
中等數(shù)學(xué)(2018年4期)2018-08-01 06:36:34
中學(xué)生數(shù)理化·七年級數(shù)學(xué)人教版(2016年9期)2016-12-07 08:28:52
中學(xué)生數(shù)理化·七年級數(shù)學(xué)人教版(2016年8期)2016-12-07 07:25:19
大眾攝影(2016年8期)2016-08-01 13:15:23
足球周刊(2014年33期)2014-11-14 16:39:19
- 中學(xué)數(shù)學(xué)月刊的其它文章
- 高考數(shù)學(xué)試題中的情境設(shè)置及啟示
——以2022年高考數(shù)學(xué)試題為例* - 基礎(chǔ)隱喻數(shù)學(xué)觀下的課堂新認(rèn)知
- 優(yōu)化數(shù)學(xué)思維 簡化解幾運(yùn)算
——以2022年新高考數(shù)學(xué)II卷第21題為例 - 培養(yǎng)解題反思能力 發(fā)展數(shù)學(xué)核心素養(yǎng)
——關(guān)于一類圓錐曲線定點(diǎn)問題的探討* - 2022年北京大學(xué)強(qiáng)基數(shù)學(xué)測試第20題的探究
- 對高中統(tǒng)計(jì)教學(xué)與命題的幾點(diǎn)思考
——基于2022年新高考I卷統(tǒng)計(jì)題的源與流*

