Disorder effects in NbTiN superconducting resonators
Wei-Tao Lyu(呂偉濤), Qiang Zhi(支強(qiáng)), Jie Hu(胡潔),Jing Li(李婧), and Sheng-Cai Shi(史生才),?
1Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210034,China
2GEPI,Observatoire de Paris,PSL Universite,CNRS,Paris 75014,France
Keywords: effects of disorder, NbTiN,superconducting film, Usadel equation, complex conductivity, superconducting resonator
1.Introduction
Low-temperature superconducting materials such as NbTiN,as well as its parent compounds NbN and TiN,have attracted significant attention due to their potential applications in low-temperature detectors and circuit quantum electrodynamics.NbTiN and NbN possess a high?andTc, making them ideal for implementation in superconductor–insulator–superconductor (SIS) mixers and hot-electron bolometer(HEB) mixers.[1–3]NbTiN and TiN are also promising candidates for microwave kinetic inductance detectors (MKIDs)because of an adjustableTcand large kinetic inductance fractions.[4,5]Moreover, NbTiN and NbN are well suited for applications in circuit quantum electrodynamics due to a highTcand?, particularly in environments with strong magnetic fields.[6]These superconducting materials, however, are not immune to disorder effects on their basic parameters, such as the?,Tc, and QDOS distribution.[7–10]One kind of disorder effect, named magnetic impurities, in materials is reported to lead to the transformation of superconductors into insulators,[11]the appearance of pseudo-energy gaps, and the enhancement of pair-breaking effects in materials.[12,13]The generalized Usadel equation, which takes account of elastic scattering,non-elastic scattering,and electro–phonon coupling, is often introduced to solve diffusion, interface, and pair-breaking effects.[14]Here,we introduce the Usadel equation to simulate and describe the disorder effects in superconducting materials.
In this paper,we firstly introduce the Usadel equation and the related complex conductivity formulas.Then, we present numerical simulations by taking into consideration the Usadel equation to investigate the disorder effects on the?,Tc,QDOS,and complex conductivity of NbTiN superconducting film.Finally, we describe the experimental methodology by characterizing the disorder effects in NbTiN superconducting resonators.
2.Complex conductivity based on Usadel equation
The Usadel equation—a simplified version of the Eilenberger equation[15]— offers a more general and non-linear approach to describe superconductivity under the diffusion limit.[16]The superconducting state is described by the pairing angleθ(x,E), which is a complex function depending on space(x)and excited energy(E),in the Usadel equation.The variableθranges in magnitude from 0 toπ/2, whileθ=0 corresponds to the normal state.The QDOS of superconducting materials isNqp=N0Re(cosθ),whereN0is the QDOS in the normal state at the Fermi energy.The Usadel equation in one dimension and equilibrium can be expressed as[14]
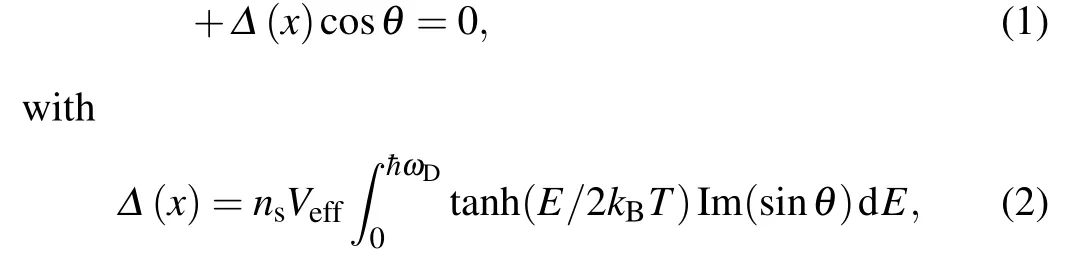
whereVeffis the BCS-like interaction potential,ˉhωDis the Debye energy,DSis the diffusivity constant,τsfis the spin-flip time,?is the usual superconducting phase,Axis the vector potential, and?is the energy gap.The first term in Eq.(1)describes the diffusion in superconductors, which is often included in interface problems.[17]The second and fourth terms describe respective energies of excitation and pairing interactions, the same as the BCS description.The third term in Eq.(1) describes the pair-breaking effects, which can lead to the smearing of coherence peaks in the QDOS and the reduction of the?.As we focus on the study of the pair-breaking effects of superconducting materials,i.e.,no diffusion and interface issues, Eq.(1) can be simplified withDS=0 as follows:
whereαis the pair-breaking parameter.
The complex conductivityσ=σ1+iσ2is a crucial parameter for calculating the surface impedance of a superconducting film and characterizing electromagnetic responses of superconducting detectors.The classical superconductors’complex conductivity was originally derived by Mattis and Bardeen,[18]and later extended by Nam to the Green’s function form of the pairing angle.[19]The extended version is written as
whereE′=E+ˉhω,f(E) is the Fermi distribution function,g1(E,E′) = Re[cosθ(E)]·Re[cosθ(E′)]+Re[i sinθ(E)]×Re[i sinθ(E′)],andg2(E,E′)=Im[cosθ(E)]·Re[cosθ(E′)]+Im[i sinθ(E)]·Re[i sinθ(E′)].In the absence of pair-breaking effects(α=0),Eqs.(4)and(5)can be simplified to the classical complex conductivity formulas.
3.Numerical simulations for disorder effects
To understand the disorder effects on the characteristics of superconducting films, it is essential to simulate their effects on key parameters, such as the?,Tc, QDOS, and complex conductivity.Disordered superconductors exhibit a phenomenon known as the smearing of the coherence peak in the QDOS distribution, described by the function of cosθ.The pair-breaking parameterαis introduced in the Usadel equation to account for the disorder effects in superconducting films.The largerαis, the lower and broader the coherence peak (E=?) in the QDOS distribution becomes.To obtain the QDOS distribution of disordered superconducting materials,cosθneeds to be solved from Eq.(3),which is essentially a quartic function about cosθ.By solving equations with the numerical solutions and considering the physical meaning of cosθ,we can calculate the complex functions cosθand sinθaboutEat a certainα.
Figure 1(a)illustrates the simulated results of QDOS distribution with respect toEfor different values ofα.Smearing of coherence peaks in the QDOS can be clearly seen, just as observed by reported results.[11]Figure 1(b)presents the distributions of cosθand sinθaboutEwhenα/?=0.05.Our numerical simulation results,obtained by solving Eq.(3),further confirm that the pair-breaking effects in superconducting materials do result in a minimum excitation energy (Eg) that is smaller than, rather than equal to, the?.According to the Abrikosov and Gor’kov model, the relationship between the pair-breaking parameterαand the minimum excitation energyEgisEg/?=(1-(α/?)2/3)3/2.[20]
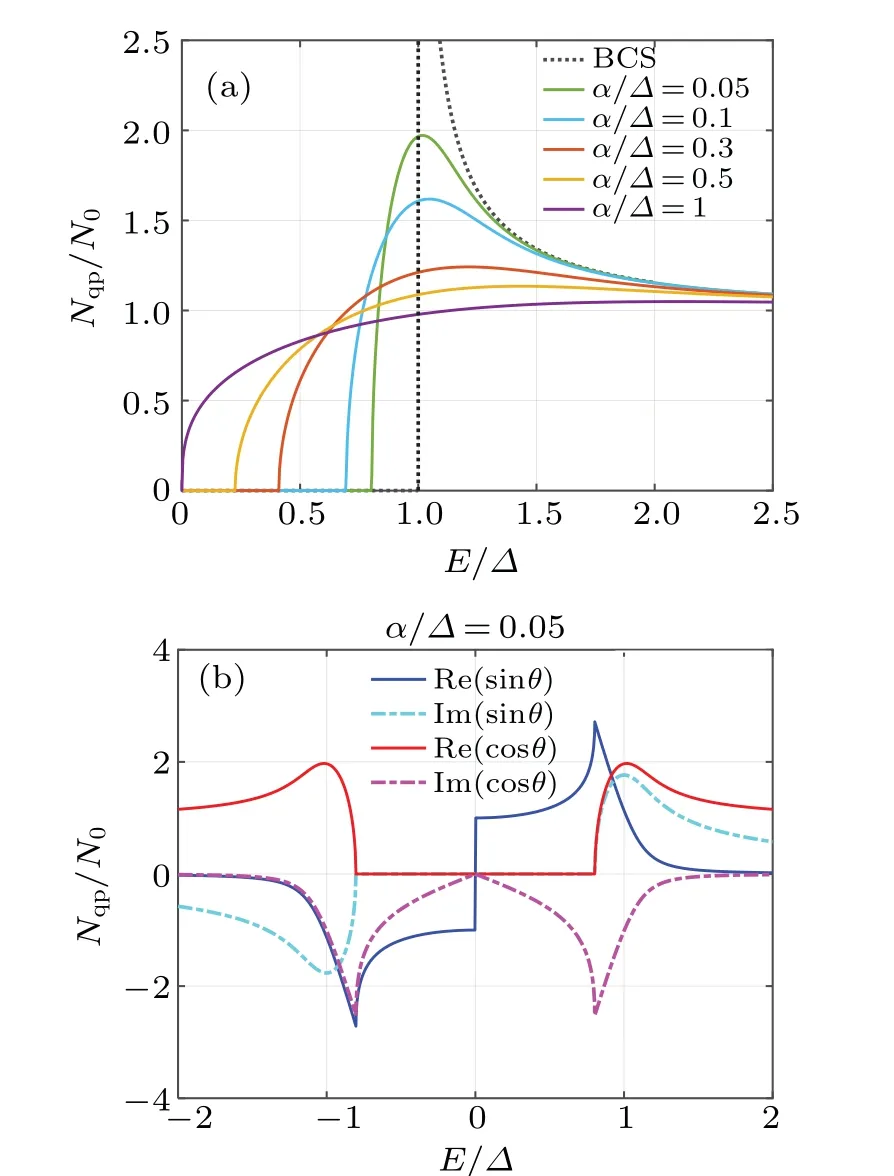
Fig.1.(a) Simulated results of the distribution of the QDOS distribution with respect to E for different values of α.(b)An example of the real and imaginary parts of cosθ and sinθ distributions about E when α/?=0.05.
As mentioned before, the?of superconducting materials also needs to be reevaluated in numerical simulations due to the pair-breaking effects.According to Eq.(2),?is related to the complex function sinθ.To solve?, we adopted iterative approaches in simulations.Using the Matsubara representation,we rewrite the formulas of?andαin disordered superconducting materials as follows:[21,22]
whereωn=(2n+1)πkBTare the Matsubara frequencies withn={0,1,2,...}.To solve?, we begin by guessing an initial value for?(here,we choose 1.76·kBTc).Next,we solve sinθ(ωn) under all Matsubara frequencies using Eq.(6).We then substitute the solved sinθ(ωn) into Eq.(7) to obtain an updated value of?until its convergence is achieved.the superconducting materials gradually decreases.Whenαexceeds 0.4?P(0), the?of superconducting materials decreases rapidly and drops to zero at 0.5?P(0),as predicted by Skalski.[11]
The simulated results indicate that pair-breaking effects have a negative correlation with theTcof the superconducting materials.The results are in accordance with the pair-breaking theory introduced by Abrikosov and Gor’kov for magnetic impurities in a superconductor.[24,25]According to the theory,theTcof the superconducting materials is written as
whereψis the digamma function.We solveTcvia numerical iterations.The simulated results are shown in Fig.3.
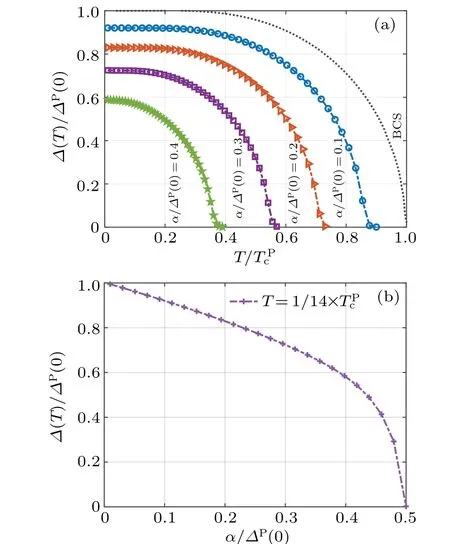
Fig.2.(a)The simulated normalized energy gap ?/?P(0)with respect to the normalized temperature T/TPc under different α.(b)Simulated results of the normalized energy gap ?/?P(0)with respect to α when T =TPc /14.

Fig.3.Simulated results of the normalized temperature T/TPc with respect to α.
Figure 2(a)shows the dependence of the normalized energy gap?/?P(0)upon the normalized temperatureT/TPcunder differentα.Here,?PandTPcdenote the?andTcof superconducting materials in the absence of the pair-breaking effects(i.e., a pure system).In this figure, the dependence of?andTbased on the BCS theory is also plotted for comparison.It can be seen clearly from Fig.2(a)that asαincreases,theTcof superconducting materials decreases at a much faster rate than?at 0 K(?(0)).Furthermore,the ratio?(0)/(kBTPc)is no longer a constant withαincreasing,as confirmed by reported scanning tunneling spectroscopy experiments.[23]Figure 2(b) shows the?of the superconducting materials as a function ofαwhenT=TPc/14.Asαincreases, the?of
Fig.4.Simulated results of σ1 and σ2 with respect to the normalized temperature T/TPc for different α, assuming f = 5 GHz and TPc =14.1 K.For reference, the dotted black line represents the simulated results using the BCS theory.
Once theTc,?,and complex functions cosθand sinθare determined via numerical simulations,we can utilize Eqs.(4)and(5)to calculate the complex conductivity of the superconducting materials.This, in turn, enables us to derive various other electrical properties.Figure 4 presents the simulated complex conductivity of the superconducting materials at a frequency of 5 GHz and theTcin a pure state of 14.1 K under differentα.The dotted line represents the simulated results based on the BCS theory for comparison.From Fig.4(a),we can see that as the temperature approaches theTc,the real part of the complex conductivity approaches one.The degradation of superconductivity with the increasing pair-breaking level is also expected,as shown in Fig.4(b).
4.Experimental characterization on NbTiN resonators
To validate our numerical simulations of superconducting materials in accounting for disorder effects, we chose NbTiN superconducting films as our subjects.To prepare our samples,we deposited a 130 nm thick NbTiN film on a 330 μm thick silicon wafer using reactive DC magnetron sputtering in a mixture of Ar and N2.Using e-beam lithography and reactive ion etching techniques,we fabricated a set of 10 planar CPW resonators that were capacitively coupled to a straight feed line on the NbTiN film.The dimensions of the CPW resonators were carefully designed,with the center conductor and gap set at 3μm and 2μm,respectively.Similarly,the center conductor and gap of the CPW feed line were designed at 10μm and 6μm,respectively.The normal state sheet resistanceRs,measured at 15 K andTc, is measured at 53.2μ?·cm and 14.1 K with our fridge,respectively.
The experimental sample,after cutting and cleaning,was mounted within a sealed gold-plated brass block connected to printed circuit boards(PCBs)with transition structures using aluminum wire bonding.The PCBs were then soldered to coaxial connectors for cable readouts.Beryllium copper pressure pads were employed to ensure an optimal thermal contact.The sample block was subsequently connected to an external vector network analyzer(VNA)through coaxial cables.Figure 5(a)provides a visual representation of the completed structures.Figure 5(b)depicts the installation of the sample on the 300 mK cold head of our adsorption refrigerator, as well as the setup and a diagram used during testing.
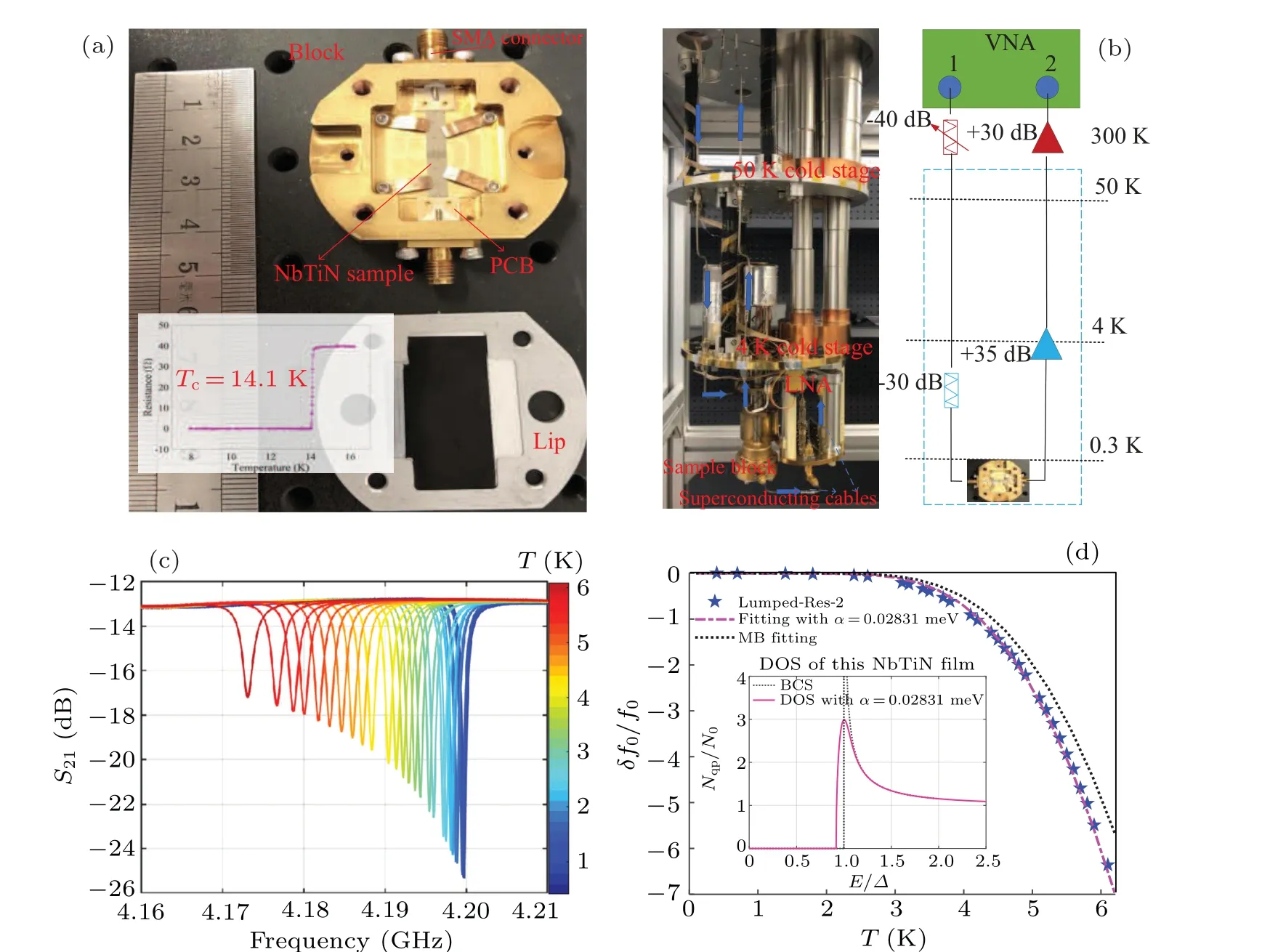
Fig.5.(a)A photograph depicting the connection and assembly of the sample chip within the block.(b)Visual representation of the sample block’s installation within the absorption refrigerator, together with a schematic diagram outlining the testing methodology.(c)Typical characteristics of one of the resonators,the absorption dip for different temperatures.(d)The relationship between the normalized resonant frequency of the resonator and the temperature.
The transmission coefficientS21of the feed line of the NbTiN sample at different temperatures was obtained using a heating device.Figure 5(c) illustrates the typical characteristics of one of the resonators, the absorption dip for different ambient temperatures.The temperature-dependent resonance characteristic is essentially induced by changes in complex conductivity,which can be expressed asδ f0/f0=αkiδσ2/(2σ2),whereαkiis the kinetic inductance fraction.[26]Consequently, the numerical simulations and the parameters of the superconducting film enable the prediction of the temperature-dependent variation of the resonant frequency of a superconducting resonator made of disordered materials.Figure 5(d) illustrates our experimental and numerical simulated results for the temperature-dependent relations of resonance frequencies.The experimental results are shown in blue stars,while the numerical simulated results are shown in pink dotted lines.In contrast, the black dotted line indicates the numerical simulated results using BCS theory.It can be seen that for our NbTiN sample with disorder effects,our numerical simulations that take the Usadel equation into consideration are more consistent with the experimental results.Based on our simulations and fitting results, the pair-breaking parameterαof our NbTiN sample is determined at 0.02831 meV,also corresponding to 0.013·?P(0)in our film,and the kinetic inductance fraction is 0.22.The inside figure in Fig.5(d)gives the QDOS distribution of our NbTiN sample.Note that the measuredTcof 14.1 K reflects theTcunder disorder effects.Thus,by incorporating the value ofαobtained for the NbTiN sample and by examining the relationship between theTcandα, the critical temperature in a pure stateTPcof our NbTiN sample is characterized at 14.359 K.
5.Conclusion
We have presented numerical simulations and discussions of the disorder effects on the basic parameters of the superconducting thin film, such as QDOS, the?,Tc, and complex conductivity.To validate our theoretical study and numerical simulations,we have fabricated and characterized a superconducting planar resonator composed of the NbTiN film.The disorder-induced pair-breaking parameterα=0.02831 meV and the critical temperature in the pure stateTPc=14.359 K of our NbTiN sample are successfully characterized via numerical simulations and experimental results.This study should be applicable for the characterization and optimization of superconducting resonators in the presence of disorder effects.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos.11925304 and 12020101002)and the Chinese Academy of Sciences Program (Grant No.GJJSTD20210002).
- Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution

