Junsheng Mu＊, Xiaojun Jing Hai Huang Ning Gao1 Laboratory of Biological Recognition and Information Application, Beijing University of Posts and Telecommunications,Beijing 100876, China

2 Key Laboratory of Trustworthy Distributed Computing and Service, Ministry of Education, Beijing 100876, China

Abstract: As a crucial component in Cognitive Radio (CR) networks, spectrum sensing has been attracting lots of attention. Some conventional methods for spectrum sensing are sensitive to uncertain signal and noise, its applicability is limited thereof. In this paper,a novel blind spectrum sensing method is proposed, where low-rank and sparse matrix decomposition is applied to the observation signal of a CR in the frequency domain. Then the ratio of the energy of the sparse part and the received signal in the time domain is considered as the criterion to decide whether the radio frequency band is idle by means of a comparison with a predefined threshold.The proposed method is independent of prior knowledge of signal and white noise, and has a better detection performance. Simulation experiments verify the performance of the proposed method in additive white Gaussian noise (AWGN), Rayleighand Rician channels.

Keywords: spectrum sensing; cognitive radio;OFDM; Rayleigh; AWGN

I. INTRODUCTION

WIRELESS communication [1] develops rapidly in company with computer and network technique at present. However, scarce radio frequency has been a restrictive factor of wireless communication until the Federal Communications Commission (FCC) [2] allows secondary user (SU) to opportunistically access a licensed band when the primary user(PU) is absent. PU is the licensed user prior to occupy the spectrum bands while SU is the free user that monitors the radio environment periodically and waits for opportunistic spectrum access without harmful interference to PU when PU is idle.

Spectrum sensing (SS) is a work to sense and judge whether PU is active. An evaluation scheme to a CR equipment is the detection probability and the probability of false alarm.Since a miss in the detection will cause the interference with PU and a false alarm will reduce the spectral efficiency, the optimal detection performance occurs in the case that the detection probability is maximized subject to the constraint of the false alarm probability[3].

Energy Detection (ED) is widely accepted for SS with its low computation and implementation complexity, whose main drawback is that it suffers from noise uncertainty and the detection performance degrades promptly when SNR declines. For possible removal of noise uncertainty and the prevention of mul-tipath fading and shadowing, some cooperative spectrum sensing methods are exploited.Such as, the majority voting (MV) rule [3]is formulated to jointly determine the existence of PU based on the voting of SUs. PU is considered existent if most of SUs vote for it. Nevertheless, this improves the detection performance at the expense of algorithm complexity.

The environment noise in CR networks is mainly caused by near-by unintentional transmissions and far-away intentional transmissions. The transmissions of other users are uncertain in time and space. Consequently, the numerical characteristic estimation of noise is imprecise, most likely, which is the primary reason of noise uncertainty in some methods of SS (for example ED). Additionally, fading and multipath in wireless communication complicate the problem. Fading will cause the signalfluctuates dramatically, while unknown multipath will cause coherent detection methods unreliable.

To solve the aforementioned problems, a novel blind spectrum sensing method is proposed in this paper, where low-rank and sparse matrix decomposition (LSMD) [4] is applied.The ratio of the energy of the sparse part and the received signal in the time domain is considered as the criterion to decide whether the radio frequency band is idle by means of a comparison with a predefined threshold. The proposed method is insensitive to noise and signal, has a wider scope of application as well as a better detection performance. Simulations based on MATLAB platform validate the effectiveness of the proposed scheme in AWGN,Rayleigh and Rician channels.

It is emphasized that LSMD differs from the other blind spectrum sensing methods,such as covariance based detection [5]. Covariance based detection mainly works based on the eigenvalue difference of the corresponding covariance matrix between the noise-only case and the signal-plus-noise case, while LSMD is established on the ratio difference of the energy of the sparse part and the received signal in the time domain after low-rank and sparse matrix decomposition.

This paper is organized as follows. Section 2 presents the primary principle of LSMD including the system model and some new definitions. Simulative experiments and performance comparisons are accomplished in section 3, followed by the conclusions in section 4.

II. THE PRIMARY PRINCIPLE OF LSMD

2.1 The primary formulation of LSMD

Let us suppose that the observation signal (of SU) y( n) is con figured with the primary signaland the ambient white noisewhileis independent of

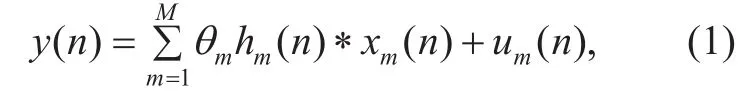
where represents the number of PU,denotes the corresponding propagation attenuation of each PU and θm={0,1} indicates the absence or presence of PU.

Then the discrete time Fourier transform(DTFT) is applied to y( n),

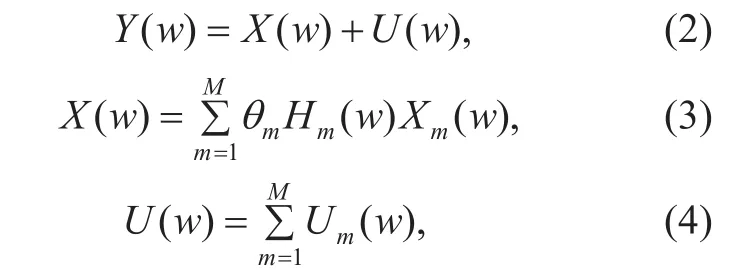
The research in [4] indicates that the AWGN in the frequency domain is low-rank and the primary signal is sparse in the frequency domain. As a result, we recover the lowrank matrix L and sparse matrix S from Y under the following constraints

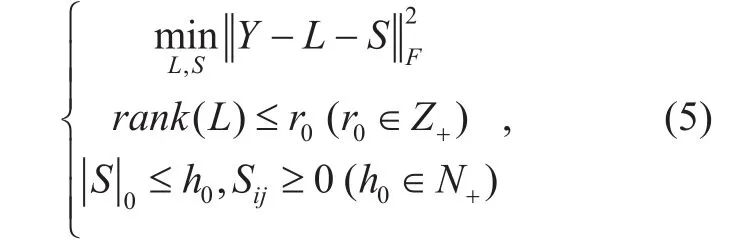
It is emphasized that (5) is the process of low-rank and sparse matrix decomposition.The main foundation of LSMD exists in that(stationary random) noise has a low-rank structure in the transform domain, such as T-F (time-frequency) and wavelet domain [6].For example, since every element in the T-F matrix is identical, the spectrogram for white noise can be assumed to be a rank-1 matrix in theory. Analogously, the periodic noise spectrogram could be treated as a low-rank matrix due to its repetitious nature. In contrast with noise in the time-frequency domain, the signal is more variable (high rank) and relatively sparse. Additionally, S is constrained to have non-negative elements, because the spectral magnitude of PU signal is physically a non-negative value [7]. If we do not impose non-negativity on S, it may result in extra interference due to the occurrence of negative elements in S. Usually, rank( L) is a positive integer smaller than r0owing to the low-rank property of the white noise spectrogram in practice. The determination of r and p will be discussed later.

In the following, an alternating projection optimization algorithm [8] is introduced to solve (5),

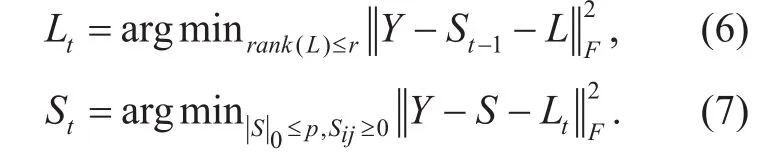
Actually, Ltand Stare updated by Y ? St?1and Y?Lt, respectively. However, for an estimation of sparse matrix St?1, the minimization in (6) over L is to learn a rank-r matrix from the partial observations. This is a fixed rank approximation problem, which could be computed by singular value hard threshold of Y ? St?1,

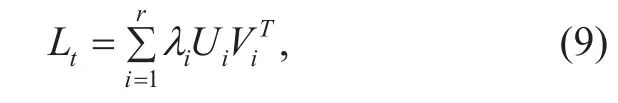
where U and V are two orthogonal matrices holding the left and right singular vectors of Y ? St?1, and Λ is the corresponding singular value matrix.

In addition, the estimation of S could be conducted by using a hard-threshold function[9], which is formulated as

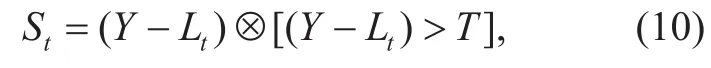
where ? is an element-wise multiplication and T is the judgment threshold of the hard-threshold function.

After the convergence of Ltand St, the Inverse discrete time Fourier transform (IDTFT)is conducted to L and S, and the observation matrix of SU could be converted into two corresponding parts in the time domain: the lowrank part l( n) mainly representing noise and the sparse part s( n) primarily representing the key information of PU,

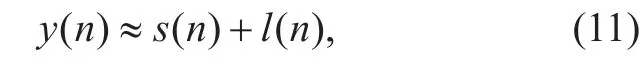
The average energy of y( n), s( n) and l( n)is defined as,

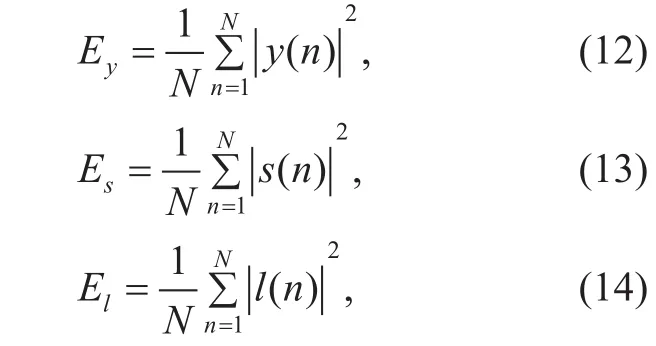
where N is the sampling number of SU terminal.

Spectrum detection can be described as a classical hypothesis testing, where H0states that there is no primary signal in a certain band and H1represents the presence of the primary user. In H0case,the ratio of Esand Eyis equal to the threshold γ for appropriate r0and p0;on the contrary, when PU is present (in H1case), the ratio of Esand Eyis obviously above the threshold under the same condition. As a result, the ratio of Esand Eycould be treated as the criterion to determine whether PU exists,

Finally, we give the definition of detection probability and false alarm probability as fol-lows,

It is stated that the similar conception(LSMD) has appeared in speech enhancement[6]. However, this is the first time to be employed in SS like this. The LSMD could even serve as a novel framework of spectrum sensing, where white noise could be regarded as a low-rank component and the key information of primary signal could be considered to be sparse in the frequency domain. The ratio of the energy of the sparse part and the received signal in the time domain is considered as the criterion to decide whether the radio frequency band is idle by means of a comparison with zero. The LSMD method is independent of the noise variance and robust to some strong noise environment therefore. Noteworthily, the LSMD method dramatically differs from some existing algorithms using the similar decomposition. S. Hou et al [10] proposed a spectrum sensing algorithm considering the covariance matrix of received signal as a combination of a low-rank matrix and a sparse matrix and the PU was detected if the discrepancy between two recovered low-rank matrices was smaller than a predefined threshold. Subsequently, Y.Han et al [11] explored a novel criterion based on the ratio of the power of the low-rank and sparse matrices to decide the presence or absence of PU in a certain band of interest.

The work in [10,11] is suitable for the white noise case where the covariance matrix of the white noise is proportional to the identity matrix in the time domain, while the LSMD method works in the frequency domain based on the low-rank nature of white noise spectrogram. Furthermore, the complexity of the LSMD method is lower than the state of the art for that the LSMD method only requires DTFT and IDTFT with the complexity O( Nlog(N)) except the process of LSMD,while the complexity of the two mentioned methods is

2.2 Related parameters

In this part, the sparse parameter p, the lowrank constraint r and the judgment threshold T in (10) are mainly discussed.

The hard-threshold T works as the judgment threshold of the sparse component in matrix S and determines the magnitude of the sparse component. Factually, the sparse parameter p has the negative correlation with the hard-threshold T. When T increases, p decreases; and when T decreases, p increases. The low-rank constraint r determines the energy of the sparse component. For a large r, the energy of the low-rank component is large and the energy of the sparse part is small. Empirically,r=1,2,3,4 for the lowrank specialty of AWGN, and p=0.5,T=0.2 for convenience to discuss their influence on the detection performance. In the following,the influence from the sparse parameter p,the low-rank constraint r and the judgment threshold T on the detection performance is considered.

As shown in figure 1, the influence of T on the detection performance keeps similar as T varies. The reason for this phenomenon is that T affects the sparsity of each iteration in (6)and (7), but has little effect on thefinal sparsity of matrix S, which is mainly influenced by the low-rank constraint r and iteration times.Generally, T≥0 is the basic requirement for widely accepted white noise environment. The low-rank constraint r determines the energy of the sparse component. For a large r, the energy of the low-rank component is large and the energy of the sparse part is small.

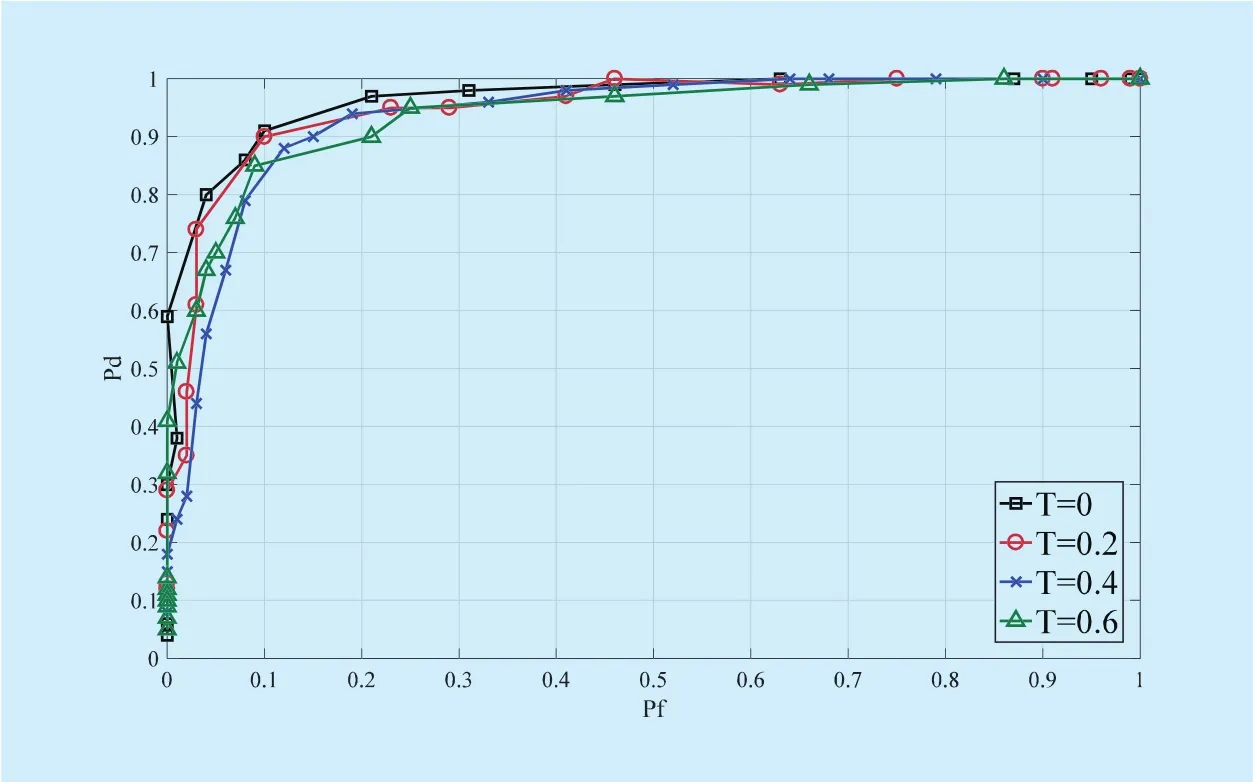
Fig. 1. The influence of sparse parameter on detection performance (signal type:OFDM signal; Channel type: Rayleigh fading channel; SNR:-10dB; r=3).

Figure 2 exhibits how the low-rank constraint r influences the detection performance.From figure 2, the selection of r greatly influences the detection performance and the detection performance improves as the rise of r. Obviously,r=3 or r=4 has a better performance than other cases. As shown in (15),the ratio of Esand Eycould be considered as the criterion to decide whether PU is present.Therefore, the selection of r influences the detection accuracy directly.

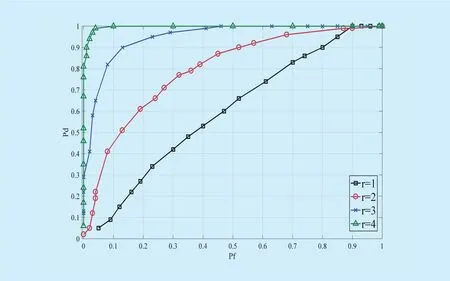
Fig. 2. The influence of low constraint on detection performance (signal type:OFDM signal; Channel type: Rayleigh fading channel; SNR:-10dB; T=0.2).

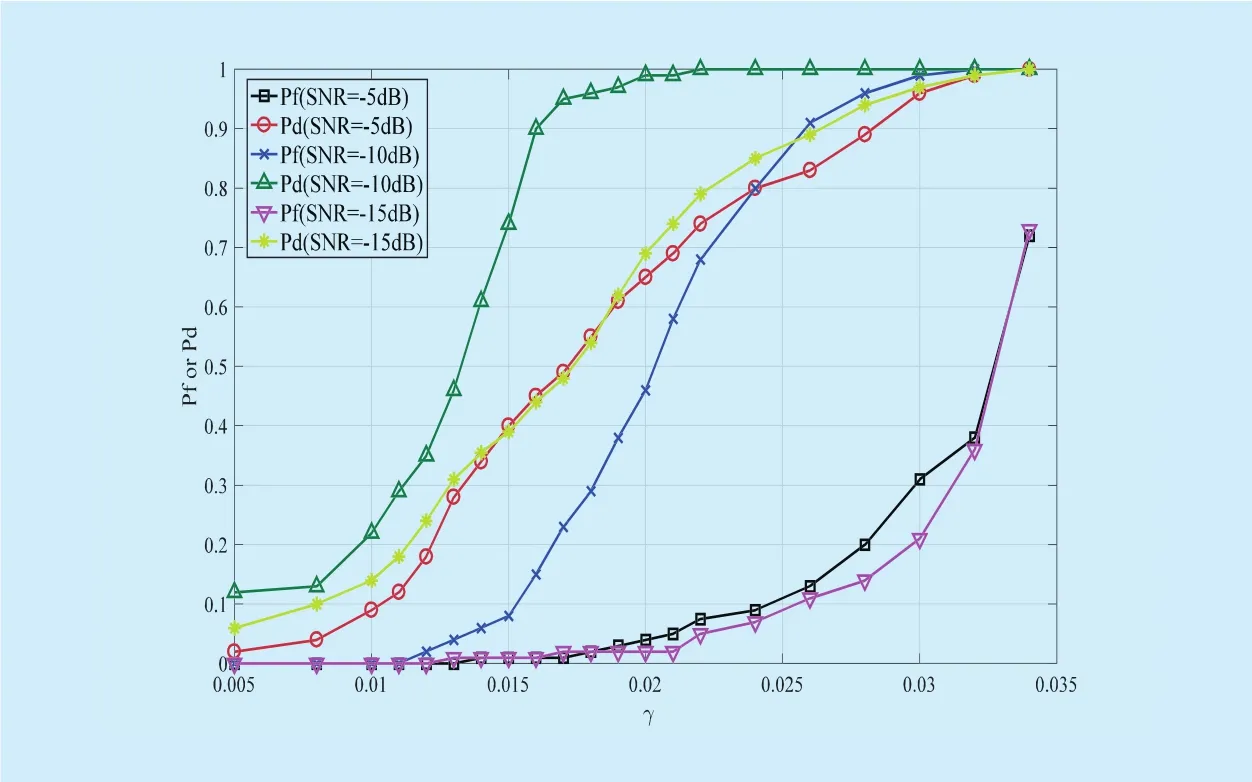
Fig. 3. The change of Pd and Pf when γ varies under vaious SNRs (signal type:OFDM; Channel type: Rayleigh; T=0.2; r=3).

In radio environment, the noise of propagation channel is generally regarded as white Gaussian. As a result, the spectrogram for white noise can be assumed to be a rank-1 matrix in theory, However, the influence from signal fluctuation, some other kinds of noise and the decomposition error of LSMD alter the rank of matrix L, just as shown in figure 2, where r=3 or r=4 has a better detection performance than others.

2.3 The estimation of detection threshold

As discussed in (15),γ is taken as the criterion to decide whether the radio frequency band is idle. In this subsection, we evaluate the detection threshold γ in theory and practice.

For appropriate r0and p0, l( n) contains the whole background noise and s( n) contains all the signal in ideal conditions, where the energy of s( n) in H0case is equal to zero.Consequently,the ratio of Esand Eycould be denoted as

That is, γ=0 in theory. Next, we will check it in practice.

Figure 3 exhibits the influence of γ on detection performance under various SNRs in practice. From figure 3, when γ varies from 0 to 0.03, Pdchanges from 0 to 1, which indicates the detection performance is sensitive to the threshold γ. Different from the case γ=0 in (18), γ=0.015 has a better detection performance considering both Pdand Pf.This is mainly due to the decomposition error of LSMD, which is our target of next work.For the case of different SNRs, the detection performance is basically similar except the case when SNR=?10dB. The LSMD method is independent of noise variance estimation,so that this may be caused by the signalfluctuation or other factors of the certain radio environment.

Figure 3 exhibits the influence of γ on detection performance under various SNRs in practice. From figure 3, when γ varies from 0 to 0.03, Pdchanges from 0 to 1, which indicates the detection performance is sensitive to the threshold γ. Different from the case γ=0 in (18),γ=0.015 has a better detection performance considering both Pdand Pf. This is mainly due to the decomposition error of LSMD, which is our target of next work. For the case of different SNRs, the detection performance is basically similar except the case when SNR=?10dB, where a performancefluctuation occurs,slightly better than the case SNR=?5dB and SNR=?15dB. This may be caused by the signalfluctuation or decomposition error, etc. To sum up, the detection performance is basically insensitive to the change of SNR, for the reason that the LSMD method is independent of noise variance estimation compared with ED.

Table 1 shows the influence of γ on detection performance under different channel environments including AWGN, Rayleigh and Rician channel, where the false alarm probability is under 0.1. Obviously, the LSMD method is suitable to the whole mentioned sensing environments. Additionally, the threshold γ is basically in accordance with the H1case in (15)under various channel environments. However, the same as the case above mentioned,γ=0.015 has a better detection performance,which is suitable for the white noise based AWGN, Rayleigh and Rician channel.

It is noted that the appropriate threshold in practice is 0.015 while it is 0 in theory.The possible reasons for the this difference are rooted in signal fluctuation, some other kinds of noise and the decomposition error of LSMD. In the further work, these factors will be considered for a possible improvement on detection performance.

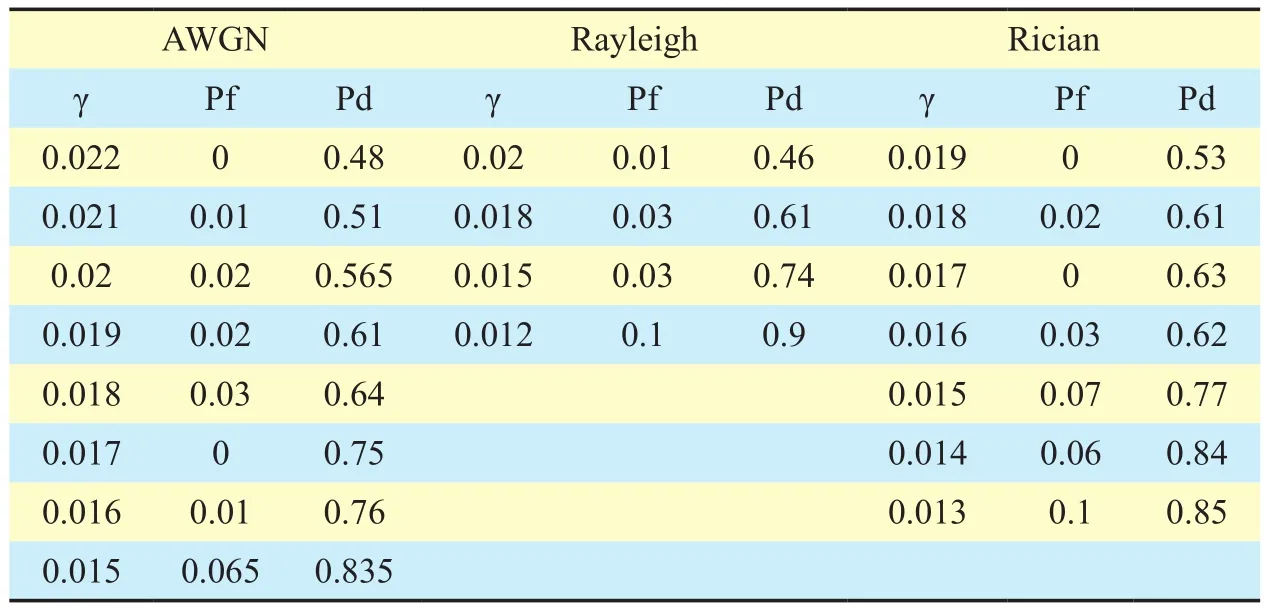
Table 1. The influence of γ on detection performance under different channel environments (signal type OFDM signal; low-rank constraint: r=3; sparse constraint:T=0.2; SNR:-10dB)

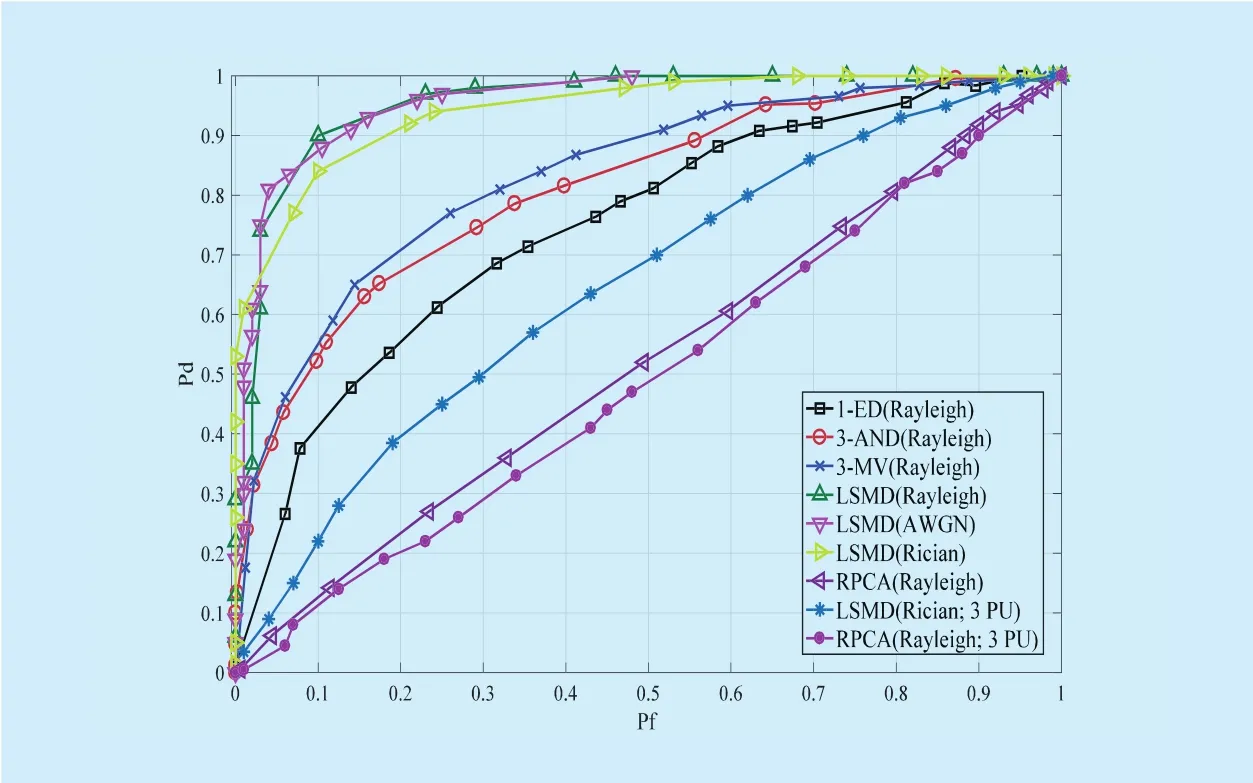
Fig. 4. Detection performance comparison of various methods for SS(SNR=-10dB).

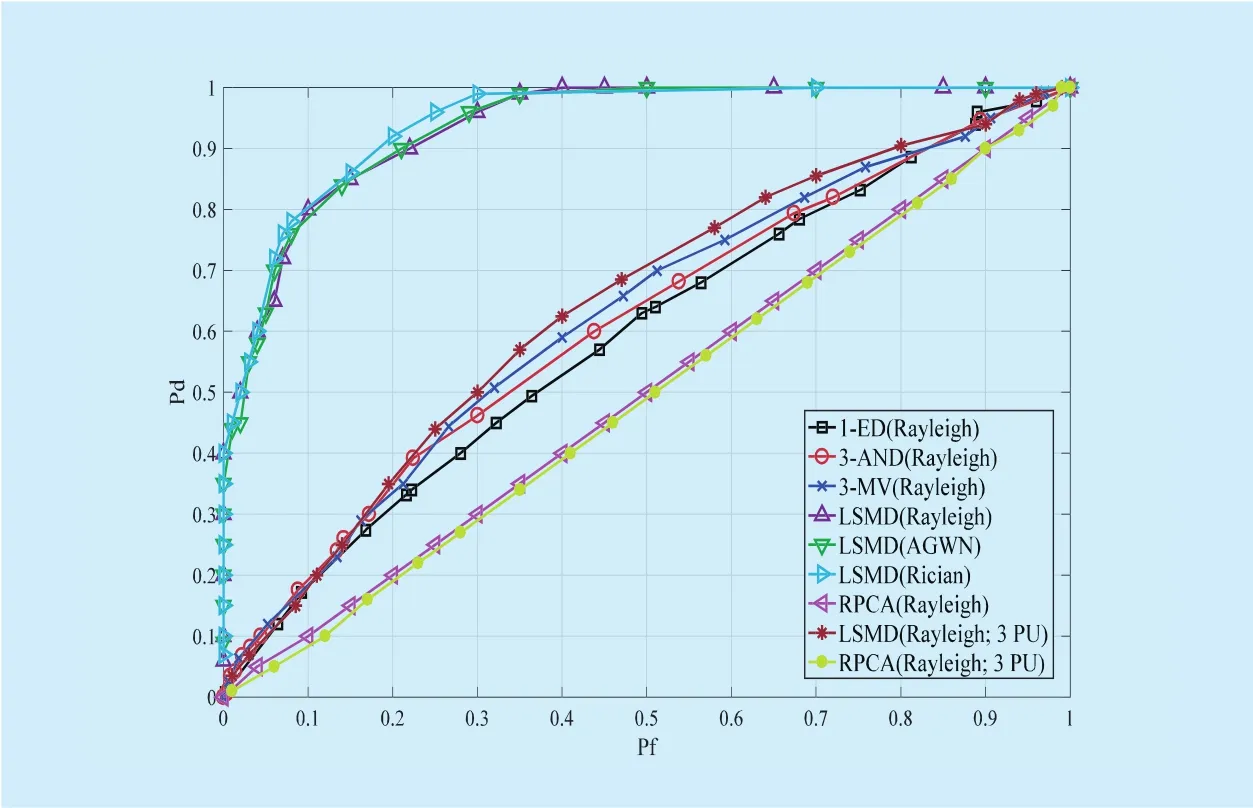
Fig. 5. Detection performance comparison for various methods for SS(SNR=-15dB).

III. SIMULATION AND PERFORMANCE ANALYSIS

In this section, simulations based on MATLAB platform are made to examine the performance of LSMD. Orthogonal Frequency Division Multiplexing (OFDM) signal is chosen as the test signal (PU) for its generality and popularity in wireless communication networks,whose center frequencyand the sampling frequency fsis the same as the bandwidth (W) of the primary user,T is fixed to be 0.2 and r is set as 3 for convenience. Additionally,the Doppler shift in both Rayleigh and Rician channel is set as 250, the Rice factor in the Rician channel isfixed as K=3 and N=100.Figure 4 shows the detection performance comparisons among different methods when SNR=?10dB, including 1-ED (energy detection of single SU), 3-AND (AND rule of 3 SUs), 3-MV (MV rule of 3 SUs) [3], and LSMD (in the Rayleigh, AWGN, Rician channel, respectively). In the Rayleigh channel,the LSMD method has a distinct performance improvement compared with other methods,which indicates the superiority of LSMD method for spectrum sensing. For LSMD method under different channel environments(the noise obeys Rayleigh, AWGN or Rician distribution), the detection performance does not have a great difference, which implies the wide application and strong robust of the LSMD method. In addition, the performance of the LSMD method outperforms the method in [10] (named RPCA here for short) for the same scene, reflecting some advantages on the capacity of discovering spectrum holes. Simultaneously, multiple PU situations are also considered between the LSMD and RPCA method. Although, the detection performance is dramatically affected by interference of the other PUs at the same frequency, the LSMD method also shows its superiority.

As a supplement, Figure 5 exhibits the detection performance of various methods when SNR=?15dB. From figure 5, the conventional ED based method has a remarkable performance decline for the rise of noise uncertainty in Rayleigh channel compared with the case of SNR=?10dB while the LSMD method has a preferable detection performance. For different channel environments and multiple PU case, the proposed LSMD method still has a good stability and performance in comparison with the corresponding other methods, which validates our discussion in figure 4.

IV. CONCLUSIONS

In this paper, the low-rank and sparse matrix decomposition is applied to spectrum sensing,where background noise is considered to be low-rank and the key signal information is treated to be sparse in the frequency domain.We judge whether the primary user is active by a comparison between the ratio of the energy of the sparse part and the received signal in the time domain and a predefined threshold.The proposed method basically overcomes the influence from noise uncertainty and could work as a novel framework of spectrum sensing. Further discussion and optimization will be made next.

ACKNOWLEDGMENT

This work is supported by the open project fund (No. 201600017) of the National Key Laboratory of Electromagnetic Environment and NSFC (No.61471066), China.