A Stackelberg Differential Game Based Bandwidth Allocation in Satellite Communication Network
Jingtao Su, Shengsong Yang, Haitao Xu*, Xianwei Zhou
School of Computer and Communication Engineering, University of Science and Technology Beijing, Beijing 100083, China
Abstract: In this paper, a Stackelberg differential game based approach is proposed to solve the bandwidth allocation problems in satellite communication network. All the satellites are divided into two groups, one has high download requirements, and the other one has low download requirements. Each satellites group has its own controller for bandwidth allocation, and can get payments from the satellites for the allocated resources. The relationships between the controllers and satellites are formed as a Stackelberg game. In our model,differential equation is introduced to describe the bandwidth dynamics for the whole satellite communication network. Combine the differential equation and Stackelberg game together,we can formulate the bandwidth allocation problems in satellite communication network as a Stackelber differential game. The solutions to the proposed game is solved based the Bellman dynamic equations. Numerical simulations are given to prove the effeteness and correctness of the proposed approach.
Keywords: stackelberg equilibrium; bandwidth allocation; differential game; satellite communication networks
I. INTRODUCTION
Satellite communication network has become a hot research topic as it can provide more extensive network coverage and multiple broadband access compared to the traditional ground networks [1]. The satellite communication network can supply multimedia services to satisfy different users’ QoS requirements[2]. But limited by the scarce resources on the satellites, there are much more challenges in the utilization of bandwidth and energy in the satellite communication network. In this paper, we will focus on the bandwidth allocation problem in the satellite communication network, to optimally allocate the satellite bandwidth for information transmission.
Bandwidth allocation in the satellite communication networks means dynamically allocate the channel resources based on the real-time requirements [3]. Lots of researches have been down on the bandwidth allocation in satellite communication networks [4-7].In [4], the authors proposed an adaptive resource management scheme for LEO satellite networks which can support multiple classes of multimedia traffic. The bandwidth can be reserved and shared dynamically based on the proposed scheme. The bandwidth utilization of the system is improved through the proposed priority based bandwidth adaption strategy. In [5], based on the BP neural network,the authors proposed a bandwidth allocation algorithm of traffic prediction to meets the real-time dynamic traffic requirements. The algorithm also considered the long term delay circumstances as an objective, to reduce the traffic waiting time. In [6], the authors proposed an enhanced congestion control based bandwidth management algorithm to dynamically allocate bandwidth among hosts, to improve the system performance and throughput.Ref [7] proposed a technique to enhance the available bandwidth utilization for satellite network, and a connection-oriented protocol to achieve high speed data transmission.Game theory based resource allocation problems in networks are widely studied[8-12], including Stackelberg game[8],cooperative bargaining game[9], evolutionary game[10], and so on. In this paper, we will combine the Stackelberg game and differential game together, which is named Stackelberg differential game. Differential Game, firstly proposed by Isaace [13], is one of the most practical and complex branches of game theory and can be used to solve a class of resource allocation problems, under which the evolution of the state is described by a differential equation and the players act throughout a time interval [14]. In this paper, we proposed a Stackelberg differential game based bandwidth allocation scheme in satellite communication network. The main motivation and contribution are,
(1) We consider a satellite communication network with multiple satellites that can be divided into two groups based on the download requirements. All the satellites in two different groups want to get enough bandwidth to satisfy their download requirements.
(2) For each group, there exists one controller for bandwidth allocation. The controller will announce the bandwidth price for allocation and can benefit from the bandwidth allocation through obtaining payments from the satellites in its related groups. Each satellite should pay for the allocated bandwidth based on the download requirements and the bandwidth price. Then a Stackelberg differential game for two satellites groups is constructed to formula the bandwidth allocation problems in the satellite communication networks.
(3) The controllers can control the allocated bandwidth for each satellite based on the equilibrium solutions of the proposed game. The controllers can maximize their payoff during the game process.
The whole paper is organized as follows.We will describe system model in Section II.In Section III, game analysis is given, and equilibrium solutions to the game is discussed.Section IV gives out the numerical simulation results. The work is concluded in Section V.
II. SYSTEM MODEL
2.1 Bandwidth allocation: a Stackelberg game
In this section, a differential game model of the bandwidth allocation with two satellite groups is presents. There are two groups in the satellite communication networks, one is the satellite group with higher download requirements (HDR), and the other one is the satellite group with lower download requirements(LDR). Assuming there are n satellites in the satellite group with higher download requirements, and m satellites in the satellite group with lower download requirements. They can share the same download resources, such as the bandwidth. In this paper, we wonder to formulate a Stackelberg differential game based approach for the bandwidth allocation in the satellite communication networks. The bandwidth allocation will be done for two different groups with different download requirements by the ground station, or the control satellites that can control the bandwidth, which is called the “controllers”. The controllers work as the leaders that would control the bandwidth by adopting bandwidth price. The satellites in require their bandwidth according to the bandwidth price and their requirements, and they are the followers. The controllers and satellites develop their policies at the different time,which leads to a Stackelberg equilibrium.
Let group 1 denotes the satellite group with HDR, and group 2 denotes the satellite group with LDR. Letdenotes the bandwidth required by the satellite i in group 1, anddenotes the bandwidth required by satellite i in group 2. Then we can express the revenue for the satellites in the form of the bandwidth requirements as follows,
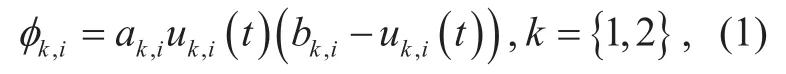
where k denotes the group number. In (1),the revenue function is imposed by two components. The first part is, which denotes the revenue earned by the satellite for the allocated bandwidth. The second partis a decrease rate. With the increase of the required bandwidth, there will be less bandwidth available for being allocated to the satellite. The parameter bk,iis the bandwidth constraint to ensure that the allocated bandwidth not exceed the total bandwidth of the satellites. Based on the revenue function given by (1), the profit of bandwidth allocation for the satellites can be expressed as
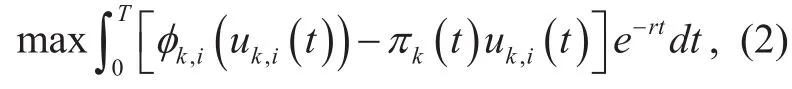
where πk(t) are the bandwidth price imposed by the controllers at time t, r is the discount rate, which is applied tofind the discount, subtracted from a future value to find the value before the game starts. e?rtis the discount factor. The discount factor should be considered when deciding whether to speed bandwidth on, or give more bandwidth for each satellite.Solving the above equations yield the optimal solutions for the bandwidth allocation in the satellite communication networks as follows,
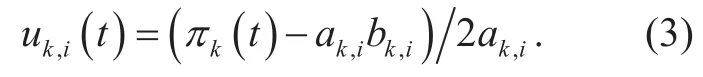
2.2 Bandwidth dynamics
The satellites in each group request the bandwidth from the satellite controllers for information transmission, and the bandwidth required by different satellites may be different.For the satellite controllers, their objectives are adopting their policies to increase the bandwidth efficiency. Meanwhile, the satellite controllers should withdraw the bandwidth that are not used by the satellites. Let x( t) denote the level of allocated bandwidth at time t, the dynamics of allocated bandwidth is governed by the following differential equation,
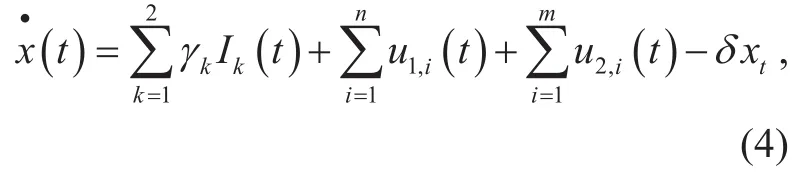
2.3 The controller’s objectives
Each satellite will be allocated an amount of bandwidth for information transmission. Once the bandwidth is allocated to one satellite,there will be less bandwidth available for the other satellites. In this paper, we assume this kind of effect is some kind of group activities.Once the bandwidth is allocated to the group 1, there will be a short-term impact (cost) on both the group 1 and group 2. For the bandwidth allocation offor group k, there will be a short-term impact (cost) ofon group 1 andon group 2. For the controllers, they will maximize the bandwidth allocation profit minus the sum of the short-term cost for bandwidth allocation. The objectives of the controller k,k={1,2} is to maximize its payoff function,
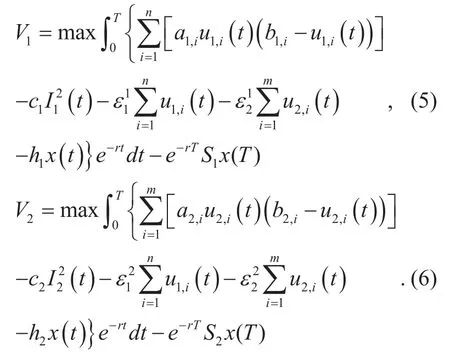
In the Stackelberg differential game, the satellites should give their decisions on the bandwidth requests based on the optimal solutions in (3). From (3), we can see that the optimal solutions are mainly controlled by the bandwidth price π1(t) and π2(t), which are imposed on the satellite controllers at time t.After the controllers announce the bandwidth price to the satellites in two groups, the satellites can make their optimal decisions on the bandwidth requests. Then the controllers in two groups can make a decision on the bandwidth price using (5-6) to maximize their payoff functions, which forms a Stackelberg game. The variablesin (5-6) are given by the solutions to (3).
III. GAME ANALYSIS
In this section, we discuss the solutions in the non-cooperative game (5) and (6). Under a non-cooperative framework, a feedback Nash equilibrium solution can be characterized as follows.
Definition 1 A set of feedback strategiesprovides a Nash equilibrium solution to the game (5) and (6) if there exist continuously differentiable functionssatisfying the following partial differential equations[15-16]:
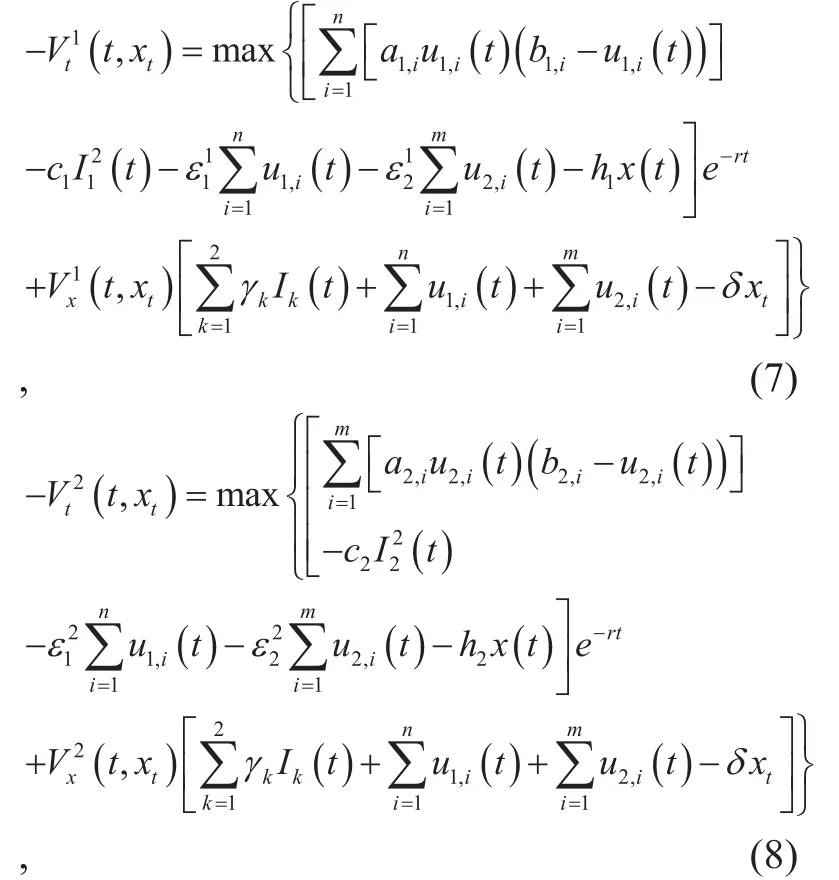
where
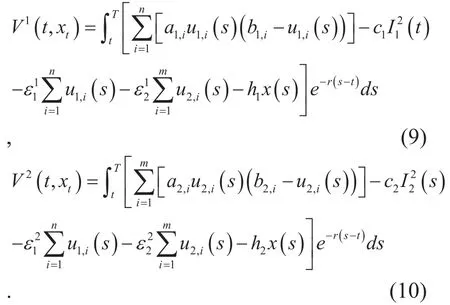
In the above equations, V1(t, xt) and V2(t, xt) are the objectives of the controllers for group 1 and group 2 during the time interval [t, T]. Based on the optimal bandwidth allocated to each satellite, which is given in (3),we can rewrite (7) and (8) as follows,
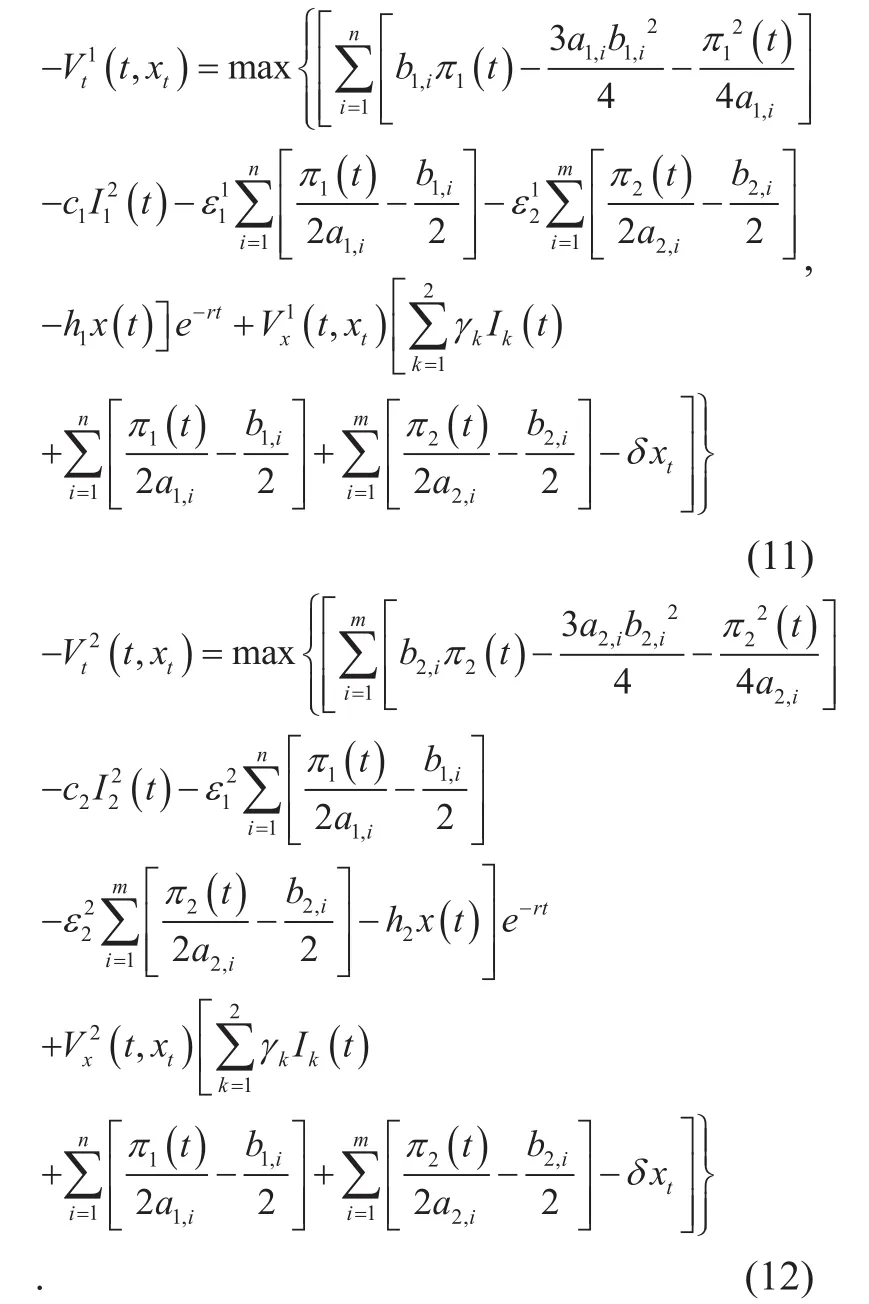
Performing the indicated maximization in(11) and (12) yields
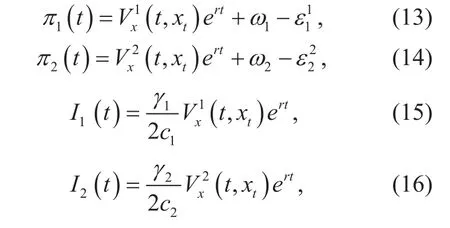
Theory 1 The payoff function Vk(t, x) of the controller k,k={1,2} during [t, T], can be obtained as:
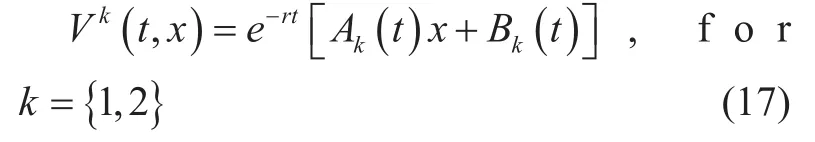
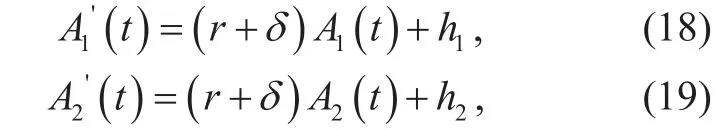
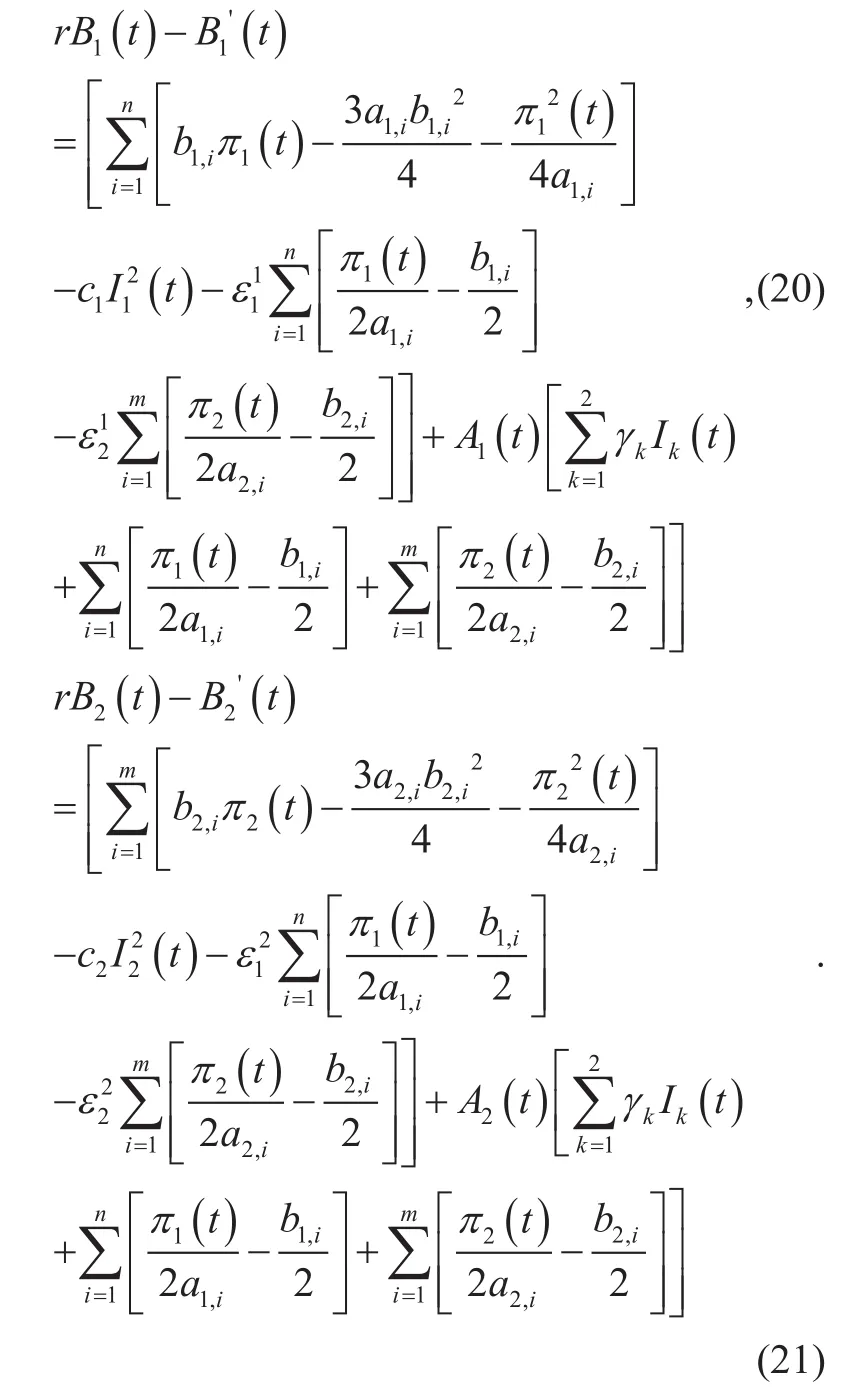
Proof.
See the appendix 1.
Based on (18) and (19), we can get thefinal expression ofas follows,
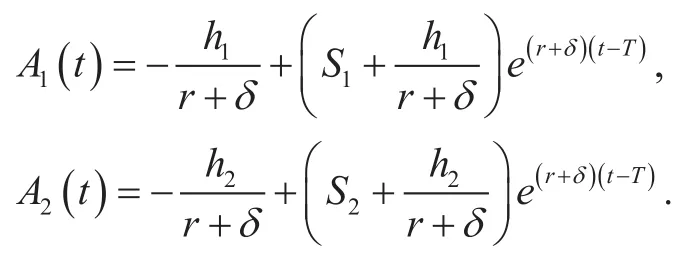
The corresponding feedback Nash equilibriums of the game (5) and (6) can be obtained as:
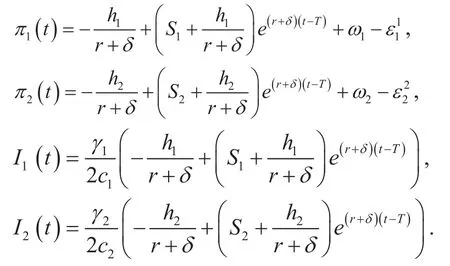
Based on the above definition and theory,the bandwidth allocation algorithm for the controllers can be given in algorithm 1.
IV. NUMERICAL SIMULATIONS
In this section, we will discuss the numerical simulations for the bandwidth allocation problems given in the Section III. We consider a satellite communication network which consists of two groups with different download requirements. Each group has two satellites, which means n=2 and m=2.The time for simulation is 60(minutes) The revenue function of satellite i in group k iswhere the parameters ak,iand bk,iare given in table 1.
In table 1, the value of b1,iis higher than that of .b2,i, because more resources should be allocated to group 1 compared to group 2. Other simulation parameters are given in table 2.

Algorithm 1. Optimal strategies for bandwidth allocation.

Table I. Setting for ak, i and bk, i.
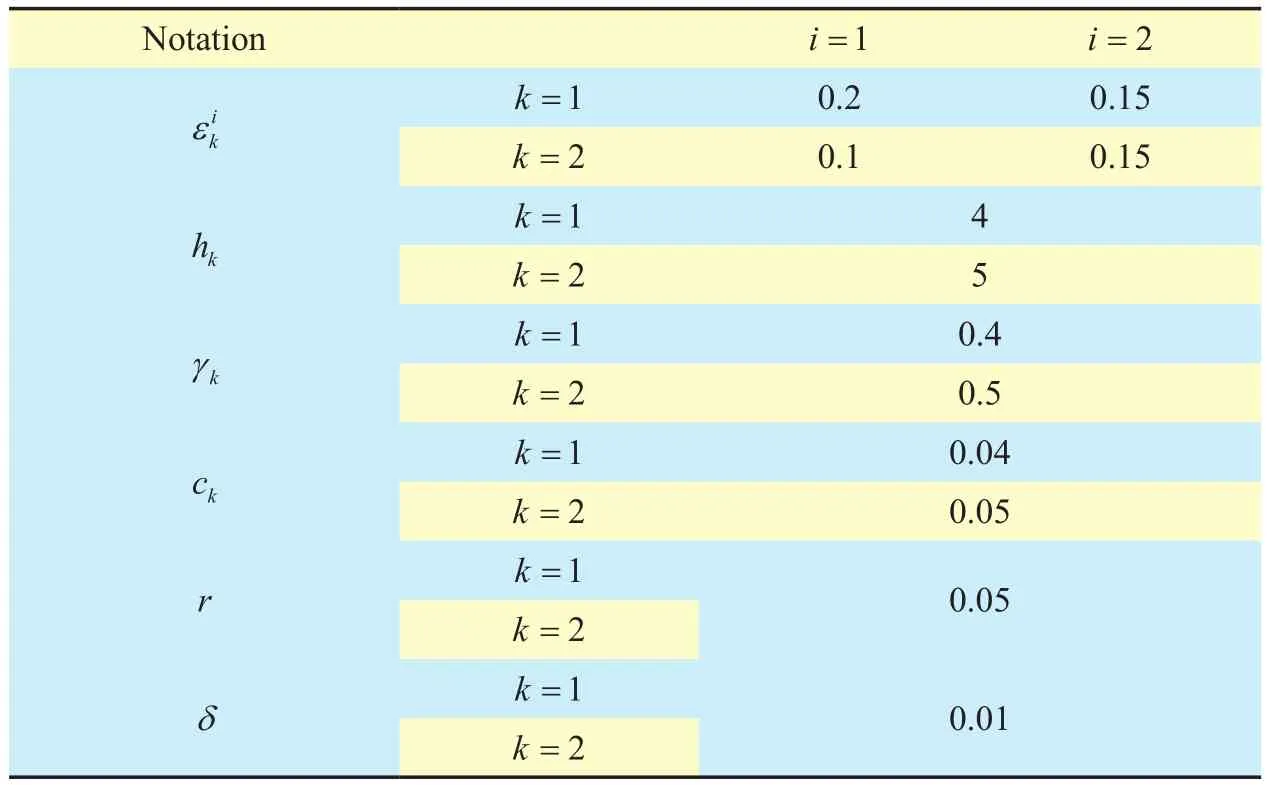
Table II. Simulation parameters.

Fig. 1. Variation of
Based on the Nash equilibrium, we can get the bandwidth withdrawn policies for each satellite group. Then we simulate the bandwidth withdrawn policies in figure 4 and figure 5.Figure 4 shows the bandwidth withdraw policies by the controllers in each satellite groups.Once the allocated bandwidth are not used by any satellite, the controllers should withdraw the bandwidth from the satellites, and prepare for the other bandwidth applications. The discount factor also affect the bandwidth withdraw policies of the satellite group, which is shown in figure 5.
For the satellites, they always focus on the allocated bandwidth, which are shown in figure 6 and figure 7. The allocated bandwidth to each satellite is shown in figure 6 and figure 7 gives the variation of the allocated bandwidth with the discount rate.
V. CONCLUSION

Fig. 2. Price variation of the satellites group.
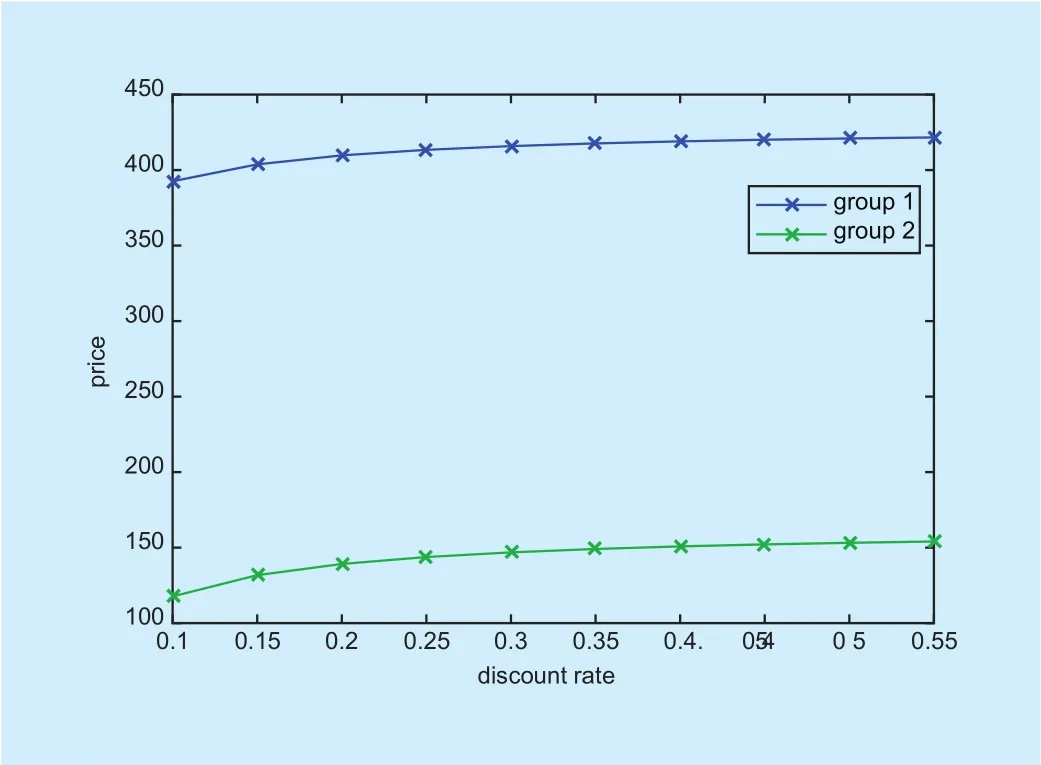
Fig. 3. Price variation with the discount factor.
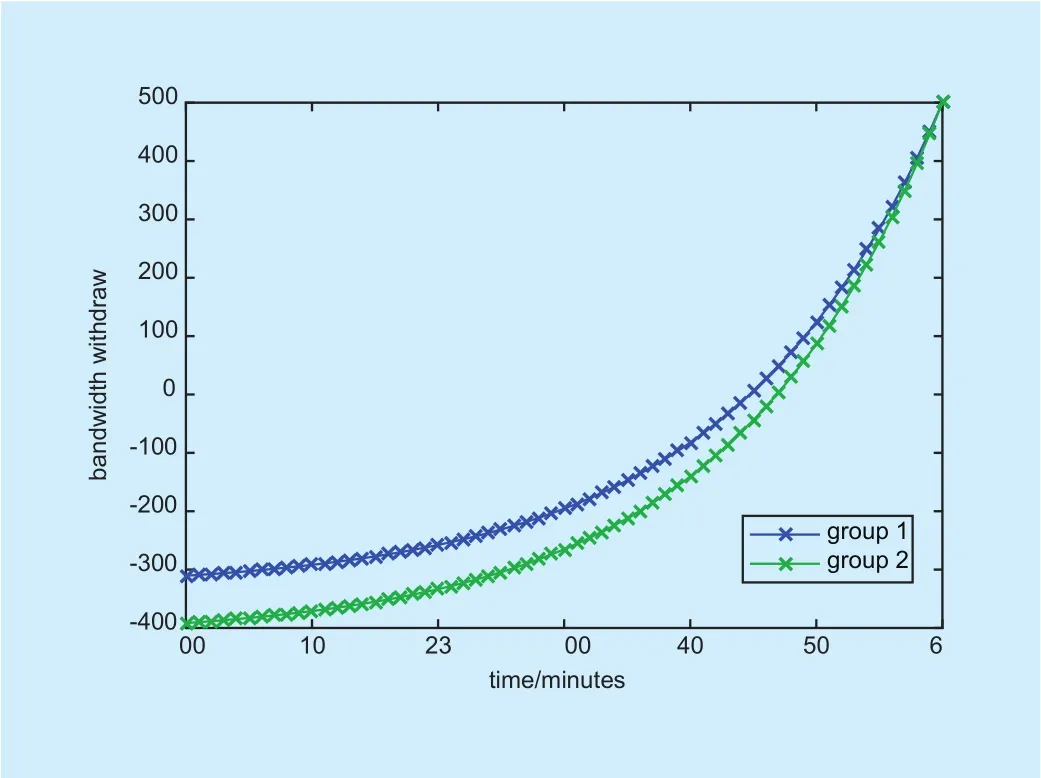
Fig. 4. Bandwidth withdraw policies of the satellites group.
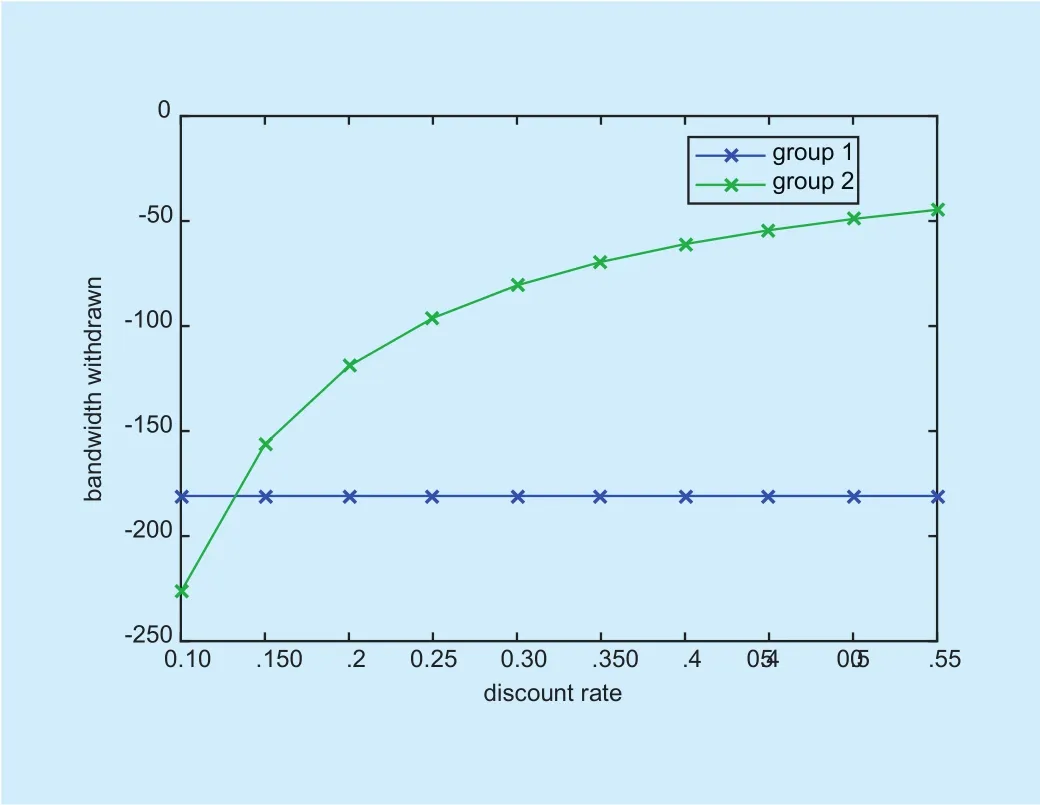
Fig. 5. Bandwidth withdraw policies on different discount factor.
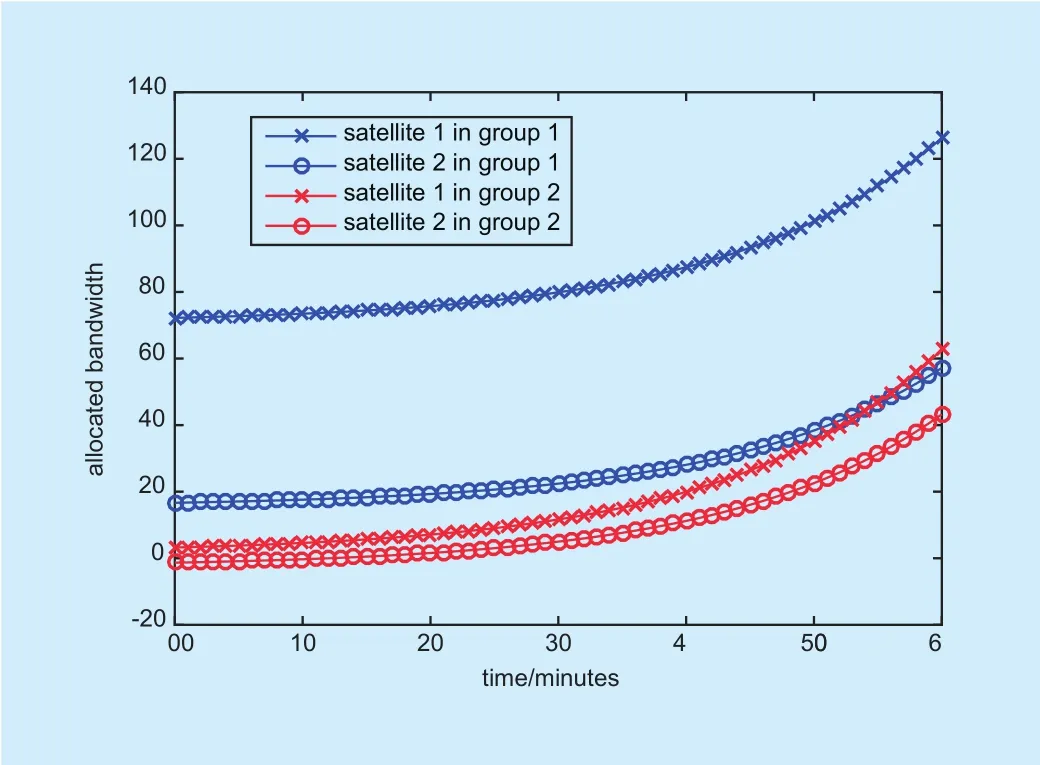
Fig. 6. Allocated bandwidth of the satellites.
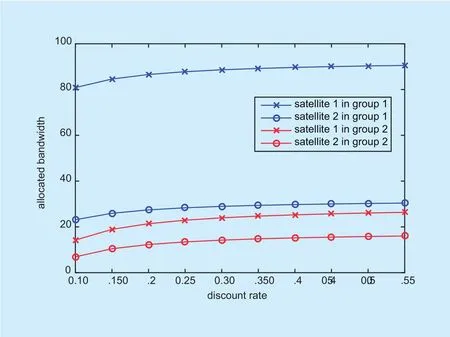
Fig. 7. Allocated bandwidth of the satellites with discount rate.
In this paper, we research the bandwidth allocation problems in the satellite communication network. In our proposed model, the satellite communication network is divided into two groups, one with high download requirements, and the other one with low download requirements. Each satellites group has its own bandwidth allocation controllers to control the bandwidth price. The bandwidth allocation problems between the controllers and satellite are constructed as a Stackelberg differential game, where the controllers are the leader which control the bandwidth, and the satellites are the followers which control their bandwidth requests based on the real-time requirements and the bandwidth price. Nash equilibrium is obtained for the proposed model to get the optimal price for bandwidth allocation. And the optimal bandwidth for each satellite can also be allocated. In future work,we will try to introduce some cooperative strategies for the satellites in different groups,and allocate the bandwidth to each satellite cooperatively. We will also attempt to combine the bandwidth allocation problem and time scheduling problem, which is more practical for the limited network resource.
ACKNOWLEDGEMENTS
We gratefully acknowledge anonymous reviewers who read drafts and made many helpful suggestions. This paper is supported by National Science Foundation Project of P. R.China (No. 61501026, U1603116).
Appendix I.
Using equations (11)-(17), system (7)-(8) can be expressed as,
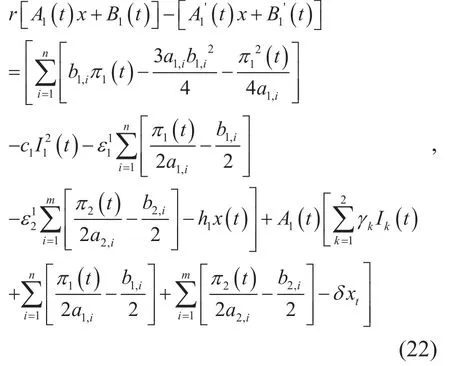
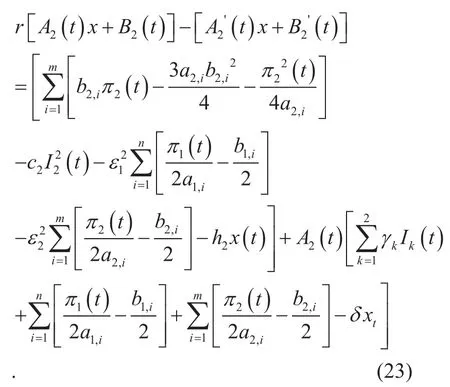
For (22) and (23) to hold, it is required that
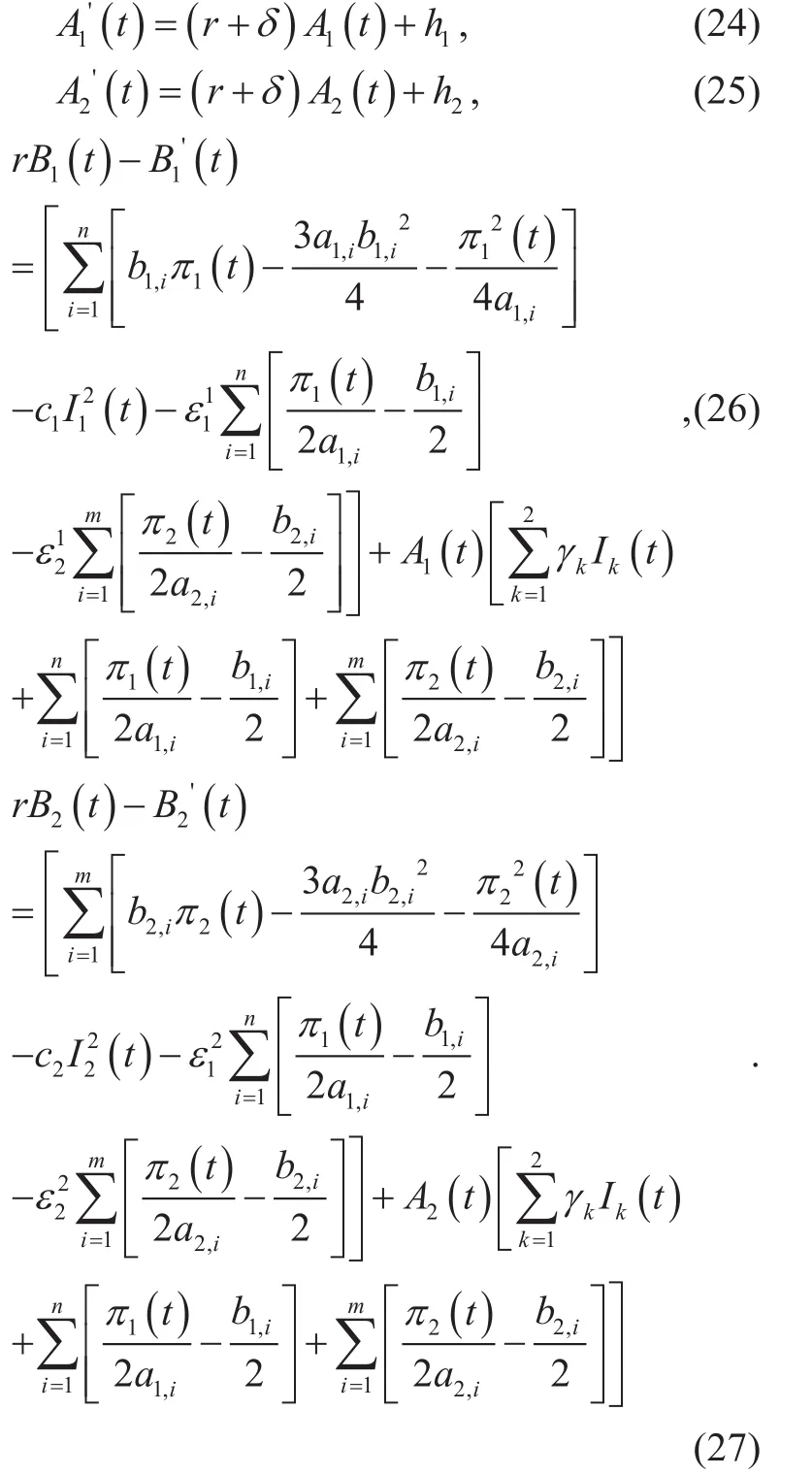
Hence Theory 1 follows.
- China Communications的其它文章
- Joint Resource Allocation Using Evolutionary Algorithms in Heterogeneous Mobile Cloud Computing Networks
- A Master-Slave Blockchain Paradigm and Application in Digital Rights Management
- The Coevolutionary Relationship of Technology,Market and Government Regulation in Telecommunications
- Mobile Jammer-Aided Secure UAV Communications via Trajectory Design and Power Control
- A Quantitative Security Metric Model for Security Controls: Secure Virtual Machine Migration Protocol as Target of Assessment
- A Blind Spectrum Sensing Based on Low-Rank and Sparse Matrix Decomposition

