An Li＊, Wenjing Zhang

Department of Electronic Information Engineering, Nanchang University, Nanchang 330031, China

Abstract: To further promote the achievable average secrecy rate for UAV-ground communications, a UAV-aided mobile jamming strategy was proposed in this paper. Specifically,an additional cooperative UAV is employed as a mobile jammer to transmit the jamming signal to help keep the source UAV closer to the ground destination, thus establishing more favorable legitimate link and enhancing the secrecy performance. We aimed to maximize the achievable secrecy rate by jointly optimizing the trajectories and transmit power of both source UAV and jammer UAV. To solve the considered non-convex optimization problem,we presented a block coordinate descent based iterative algorithm to address a sequence of approximated convex problems for the optimized parameter block by block tofind a local optimal solution. Numerical results verify that the proposed algorithm can achieve significant secrecy rate gain compared to all the benchmark schemes.

Keywords: physical layer security; UAV-ground communications; mobile jammer-aided; trajectory design; power control

I. INTRODUCTION

Facing the highly diversified application requirements in the future wireless networks[1],UAV-aided wireless communications have attracted fast-growing interest due to their many advantages, such as flexible on-demand deployment, fully-controllable mobility, lineof-sight (LoS) aerial-ground link[2], thus increasingly being applied for multifarious substantial scenarios including UAV-aided ubiquitous coverage[3-5], mobile relaying[6,7], information dissemination or data collection[8-10], energy broadcasting[11], etc.However, the open and shared nature of wireless medium, especially the feature with the LoS links between UAVs and ground nodes makes UAV communications more prone to being intercepted by ground eavesdroppers,thus bringing to a new security challenge.

Over the past few years, physical (PHY)layer security has emerged as an indispensable mechanism to enable secure wireless communications without relying on traditional cryptographic approaches[12]. Various PHY layer security schemes based on Multiple-Input Multiple-Output (MIMO), cooperative relaying, cooperative jamming, and/or power control techniques have been widely investigated to enhance the secrecy rate performance of wireless systems (see [13-16] and the references therein). However, all the above studies only considered the cases where all communications nodes are atfixed or quasi-static lo-cations, which cannot be directly extended to UAV-aided wireless systems.

Recently, the authors in[17] examined the secure UAV-ground communications in the presence of a ground potential eavesdropper by exploiting the mobility of UAV. However,it is shown in[17] that the trajectories of the UAV are not along the straight lines as the best-effort heuristic trajectories, and the hovering locations of UAV are not directly over the destination, which means the legitimate channels quality is sacrificed byflying as far away as possible from the eavesdropper to prevent eavesdropping. In fact, the advantages of UAVs also offer a new opportunity to perform mobile jamming so as to further improve the secrecy rate. First, under practical constraints on the UAV’s mobility, the UAV acted as a mobile jammer can adjust dynamically its own location as close as possible to ground eavesdroppers, and proactively jam eavesdroppers with power-aware, i.e., more power is used when it is nearby eavesdroppers but away from destinations and vice versa. Second, different from the threat arising from LoS links to the security of UAV-ground communications, the feature of LoS links with less impairment by terrestrial fading and shadowing is beneficial to make jamming more effective.

Motivated by the above studies, in this paper, we investigate a UAV-aided mobile jamming strategy to further promote the secrecy performance for UAV-ground communications. Specifically, subject to both average and peak transmit power constraints as well as the UAVs’ mobility constraints, an additional cooperative UAV is employed as a mobile jammer to transmit jamming signals to degrade the eavesdropper channel. Such a UAV-enabled mobile jammer is introduced to fly as close as possible to the eavesdropper and help the source UAV keep as close as possible to the destination, and thus enhancing the achievable secrecy rate. The achievable average secrecy rate maximization problem is addressed which jointly optimizes the trajectories and the transmit power of both source UAV and jammer UAV over afiniteflight period. To efficiently solve the non-convex secrecy rate maximization problem, an efficient iterative algorithm is proposed by employing the block coordinate descent and successive convex optimization techniques to compute the trajectories and the transmit power of both UAVs successively,thus obtaining a local optimal approximate solution. Simulation results demonstrate that the proposed joint design outperforms all benchmark schemes, especially the scheme without involving jamming in[17].

II. SYSTEM MODEL AND PROBLEM FORMULATION

2.1 System model

As shown in figure 1, we consider a UAV-ground wireless communication system where a source UAV (S) above the ground communicates with a ground destination (D) in the presence of an eavesdropper (E) on the ground over a given finite flight period T in second(s). Without loss of generality, we consider a Cartesian coordinate system with D and E located on the ground with wD=(0,0) and wE=(L,0) in meter (m), respectively, which are both known to S. To improve the secrecy rate of UAV-ground communication system, a cooperative UAV (J) is employed as a friendly mobile jammer to transmit jamming signals to confuse E, and therefore protect the source transmission over T. Note that Gaussian noise, which is the same as the additive noise at D, is considered as the jamming signals.Such jamming signals are easy to implement in practical systems for more practical cooperation since not only is no knowledge a priori required to generate it but also no extra overhead is required to eliminate it. Thanks to the mobility of UAVs, the larger T is, more time in general is provided for S (J) to move closer to D (E) to achieve better link quality and at the same time to keep farther away from E(D) for causing less information leakage (excessive interference), thus achieving a higher secrecy rate.

We assume that both UAVsfly horizontally at afixed altitude H in m and their initial/final horizontal locations, denoted byandrespectively, are pre-given depending on their launch/landing sites or pre-defined mission requirement. For ease of exposition, the UAVs’ flight period T is divided into N time slots with equal length,i.e., T=Nδt, where δtin s is chosen sufficiently small such that UAVs’ locations can be considered unchanged within each time slot[8]. Accordingly, the trajectories of both UAVs over T can be approximated by two N-length sequencesandrespectively, which satisfy the following mobility constraints:

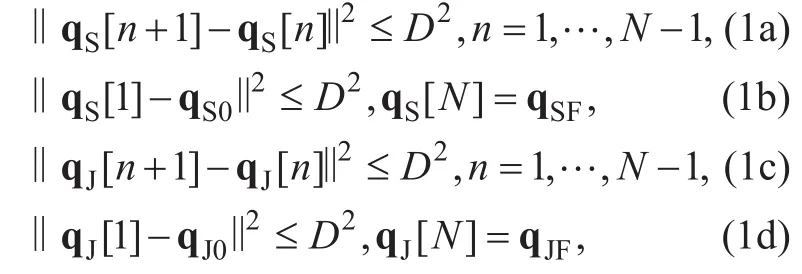
where D=Vδtis the maximum horizontal distance that each UAV can fly within each time slot at the maximumflight speed V in m/s.

The actual measurement observations in[18]have shown that the UAV-ground channels are dominated mainly by the LoS links even when the UAV flies at a moderate altitude.Thus, similar to [6, 8], we assume that the UAV-ground channel quality mainly depends on the distance between UAVs and ground users. Thus, the channel power gain from UAV i, i∈{S, J} to ground user j, j∈{D,E} at time slot n follows the free-space path loss model,given by

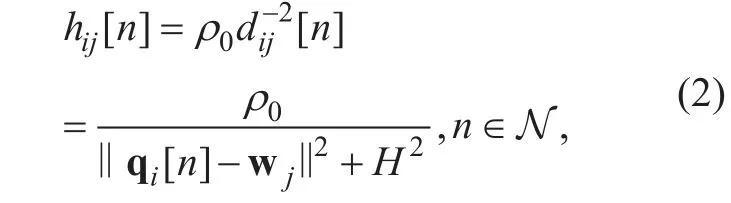
Fig. 1. A mobile jammer-aided UAV communication system.

Let PS[ n ] and PJ[ n] denote respectively the transmit power of the source UAV S and the jammer UAV J in time slot n. In practice,they are usually subject to both average/peak limits over time slots, denoted byand, respectively. Therefore, the transmit power constraints can be written as

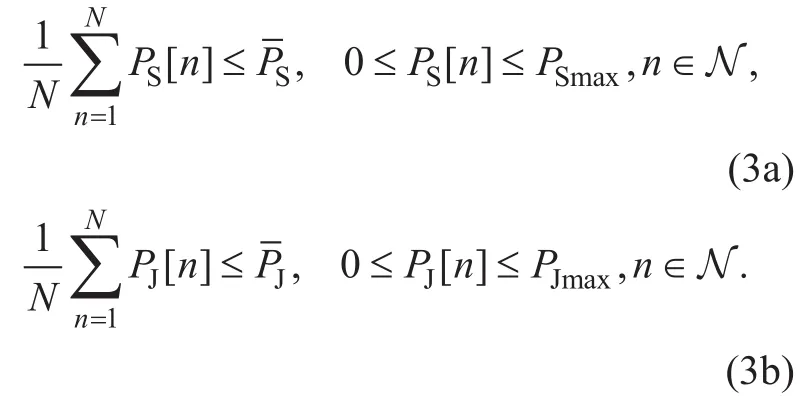
The average secrecy rate achievable of the UAV-aided jamming strategy in bits/second/Hertz (bps/Hz) over the total N time slots is given by [19]

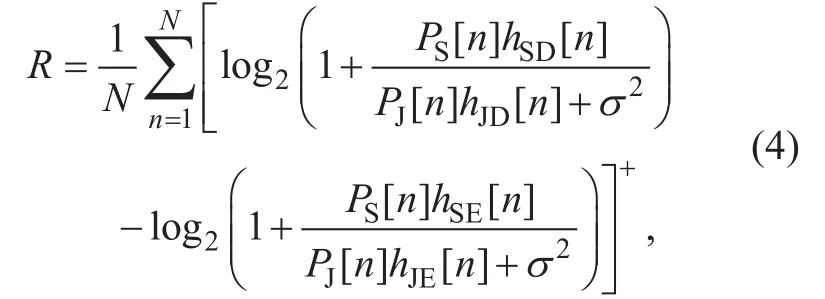
2.2 Problem formulation

Let the source UAV S’s trajectoryand the transmit power, and the jammer UAV J’s trajectoryand the transmit powerOur goal is to maximize the achievable aver-age secrecy rate in (4) by jointly optimizing both UAVs’ trajectories QSand QJ, and their respective transmit power PSand PJover all the N time slots subject to both UAVs’ mobility constraints in (1) and transmit power constraints in (3). Thus, the achievable secrecy rate maximization problem can be formulated as

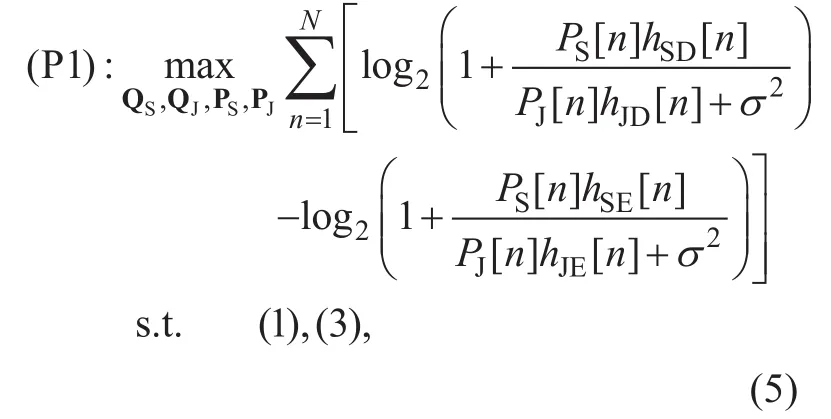
where the operation [?]+is omitted since each summation term in the objective function of(P1) must be non-negative with the optimal solution; otherwise, the value of (P1) can be always increased up to zero by setting PS[ n ]=0 without violating transmit power constraints. Although (P1) is smooth, it is still non-convex and challenging to solve. Thus,we propose an efficient iterative algorithm for (P1) which is guaranteed to converge to at least a locally optimal solution.

III. PROPOSED SOLUTION

In this section, we propose an efficient iterative algorithm for (P1) by applying the block coordinate descent and successive convex optimization techniques. Specifically, (P1) is divided into four subproblems to optimize both UAVs’ transmit power PSand PJas well as their trajectories QSand QJin an alternately iterative manner until the algorithm converges.

3.1 Subproblem 1: optimizing transmit power PS

For any given both UAVs’ trajectories QSand QJand jammer UAV’s transmit power PJ,(P1) can be expressed as

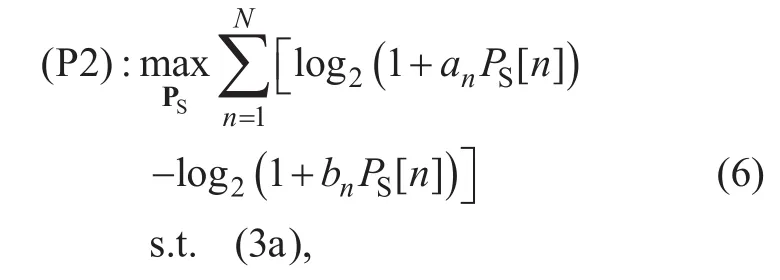
Although (P2) is non-convex with respect to PS, its optimal solution can be obtained as shown in [19]

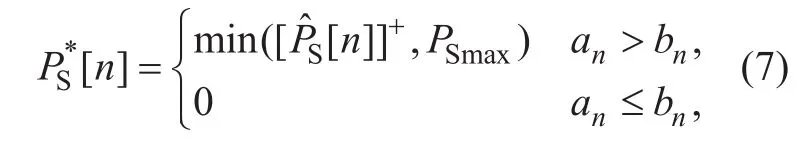
where

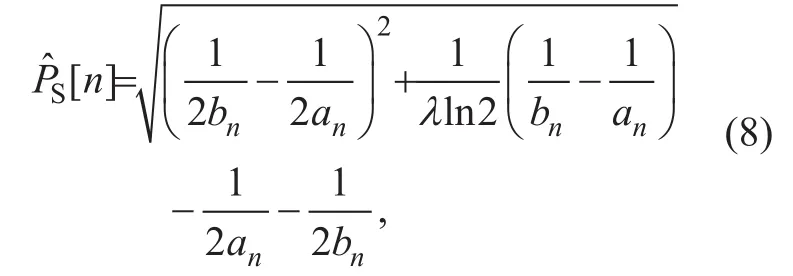
where λ is a non-negative parameter that ensureswhich can be found efficiently by applying the bisection search.

3.2 Subproblem 2: optimizing transmit power PJ

For any given source UAV’s transmit power PSand both UAVs’ trajectories QSandas

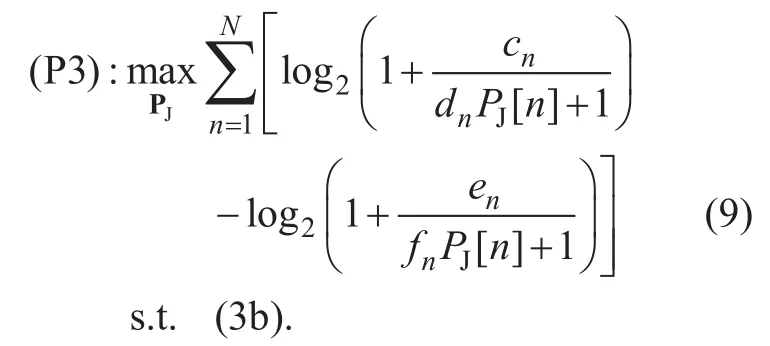
Although (P3) is still non-convex, based on the successive convex optimization tech-nique we can obtain an efficient approximate solution by successively maximizing a lower bound of (P3) at each iteration. Letdenote the given jammer UAV’s transmit power in the k-th iteration, thefirst term in (9) is lower bounded as with thefirst-order Taylor expansion

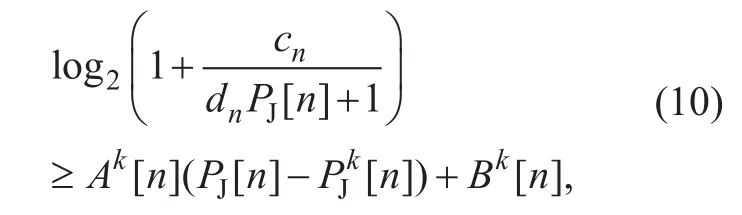
where

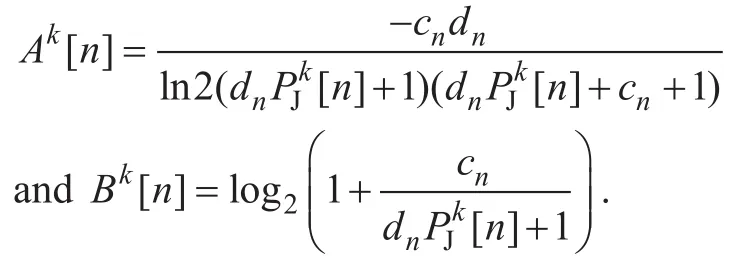
As a result, (P3) can be approximated as the following problem

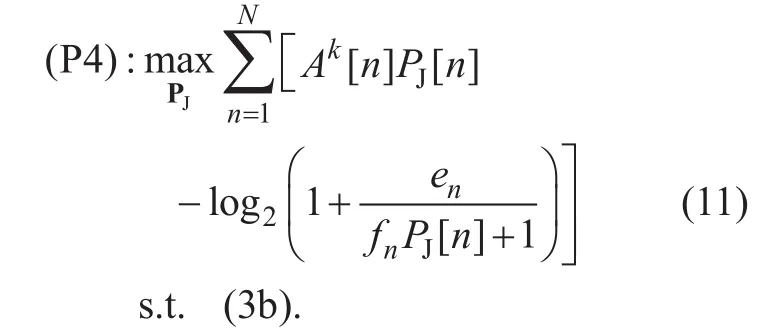
Since thefirst term in (11) is a linear function with respect to PJ, (P4) is a convex optimization problem, which can be solved optimally by the existing optimization tools such as CVX [20].

3.3 Subproblem 3: Optimizing Source UAV’s Trajectory QS

One can verify that constraints (12b) and(12c) must hold with equalities at the optimal solution, since otherwise t[ n]( u[ n]) can be decreased (increased) to improve the objective value. However, (P5) is still non-convex and thus difficult to be solved optimally.Similarly, by applying successive convex optimization technique, the termis replaced by its convex lower bound while the termby its concave upper bound at a given initial point. Definea s the source UAV’s given local trajectory in the k-th iteration, then we obtain

With (13), (P5) is approximated as

After such approximation, the objective function of (P6) is concave and its feasible region is convex, thus it can also be optimally solved by CVX.

3.4 Subproblem 4:Optimizing Jammer UAV’s Trajectory QJ

After introducing slack variablesany given both UAVs’ transmit power PSand PJand source UAV’s trajectory QS, (P1) can be recast as

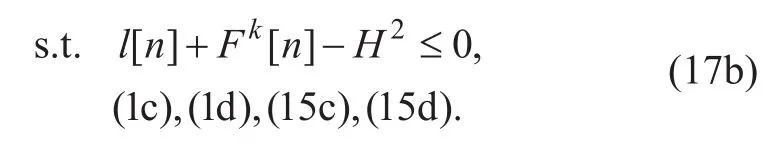
Since (P8) is a convex optimization problem, it can be efficiently solved by CVX.

3.5 Overall Algorithm

In summary, by applying the block coordinate descent method, the overall algorithm for (P1)is obtained by jointly optimizing both UAVs’transmit power PSand PJas well as their trajectories QSand QJalternately via solving four subproblems (P2), (P4), (P6), and (P8)respectively in an iterative manner. The details of the proposed iterative algorithm for (P1) are summarized in Algorithm 1.

Next, we consider the convergence of Algorithm 1. Letandbe defined as the objective values of (P1), (P4), (P6), and (P8)with any givenandrespectively. According to the step 3-6 of Algorithm 1, we have

where (a),(c),(f), and (i) holds sinceare the optimal solution of problem (P2), (P4), (P6), and (P8),respectively; (b),(e), and (h) holds since problem (P4) at, (P6) at, and (P8) athave the same objective values as that of problem (P3), (P5), and (P7), respectively by using first-order Taylor expansion; (d),(g),and (j) are true since the objective value of(P1) is lower bounded by that of (P4) at,(P6) at, and (P8) at, respectively.As a result, the objective value of (P1) with the solutions by solving subproblems (P2),(P4), (P6), and (P8) is non-decreasing over iterations. Furthermore, since the optimized value of (P1) isfinite, the proposed Algorithm 1 is guaranteed to converge.

IV. SIMULATION RESULTS

In this section, we present simulation results to verify the performance of the proposed UAV-aided mobile jamming strategy via joint trajectory design and transmit power control for UAV-ground communication (denoted by“traj. & pow. ctrl.”). We compare the proposed strategy with the following three benchmark schemes:

? traj. & avg. pow.: Only both UAVs’ trajectories are optimized by solving problem(P6) and (P8) iteratively until convergence with average transmit power, i.e.,tively.

? pow. ctrl. & line traj.: Both UAVs’ trajectories are fixed in a heuristic best-effort manner: source UAV S (jammer UAV J)first flies towards the location above D(E) at the maximum speed, then stays stationary there (if T is sufficiently large),and finally arrives its final location in the last time slot. It is noteworthy that if there is no enough time for S (J) to reach the location above D (E), it will turn at a midway pointon the line segment betweenand the point at a height of H over, which horizontal coordinate makes the sum of distances, i.e.,equals to VT}, and thenfly towards thefinal locationat the maximum speed. Both UAVs’ transmit power is optimized by solving problem(P2) and (P4).

Algorithm 1. Proposed iterative algorithm for problem (P1).

? traj. & pow. ctrl. NJ: No jammer UAV is employed as “joint traj. opt. & pow. ctrl.”in[17].

All simulation parameters are set up ascases where UAVs have different initial and final locations, denoted as Case 1 and Case 2, are considered. In Case 1, both UAVs have the same initial/final locations, which coordinates are set asm, andm, as shown in figure 2. In Case 2, both UAVs’ initial/final locations are on the parallel line connecting D and E with the coordinates as qS0=(?500,?150)m,qSF=(700,?150)m, qJ0=(700,150)m, and qJF=(?500,150)m, respectively.

First, for Case 1, Figure 2 exhibits the trajectories of both UVAs (S and J) of different algorithms for different period T. The locations of D, E, as well as both UAVs’ initial andfinal locations are marked with ○, ?, +, and × ,respectively. It is observed that when T=400 s, the minimum time required for S/Jflying at the maximum speed from the initial location to the final location, the trajectories of S (J)for all algorithms are identical. As T increases, the trajectories of S (J) for the proposed“traj. & pow. ctrl.” and the benchmark “traj.& avg. pow.” are still similar in an arced path,where Jflies in the opposite direction to S so as to efficiently jam the eavesdropper. This is because J tries tofly as close as possible to E in order to help S fly as close as possible to D. When T is sufficiently large, i.e., T=600 s, it is observed that for the proposed “traj. &pow. ctrl.”, Sfirstflies at the maximum speed to reach a point closer to D, then remains stationary there as long as possible, andfinally in an closer arced path to Dflies at the maximum speed towards thefinal location and reaches it in the last time slot than that for “traj. & pow.ctrl. NJ”. These stationary points closer to S strike a better balance between enhancing the legitimate channel and causing less leakage to E, thus achieving the larger maximum secrecy rate than that of “traj. & pow. ctrl. NJ”.

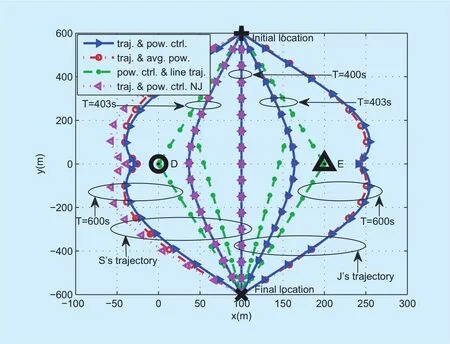
Fig. 2. Trajectories of UAV-enabled S and J in case 1.

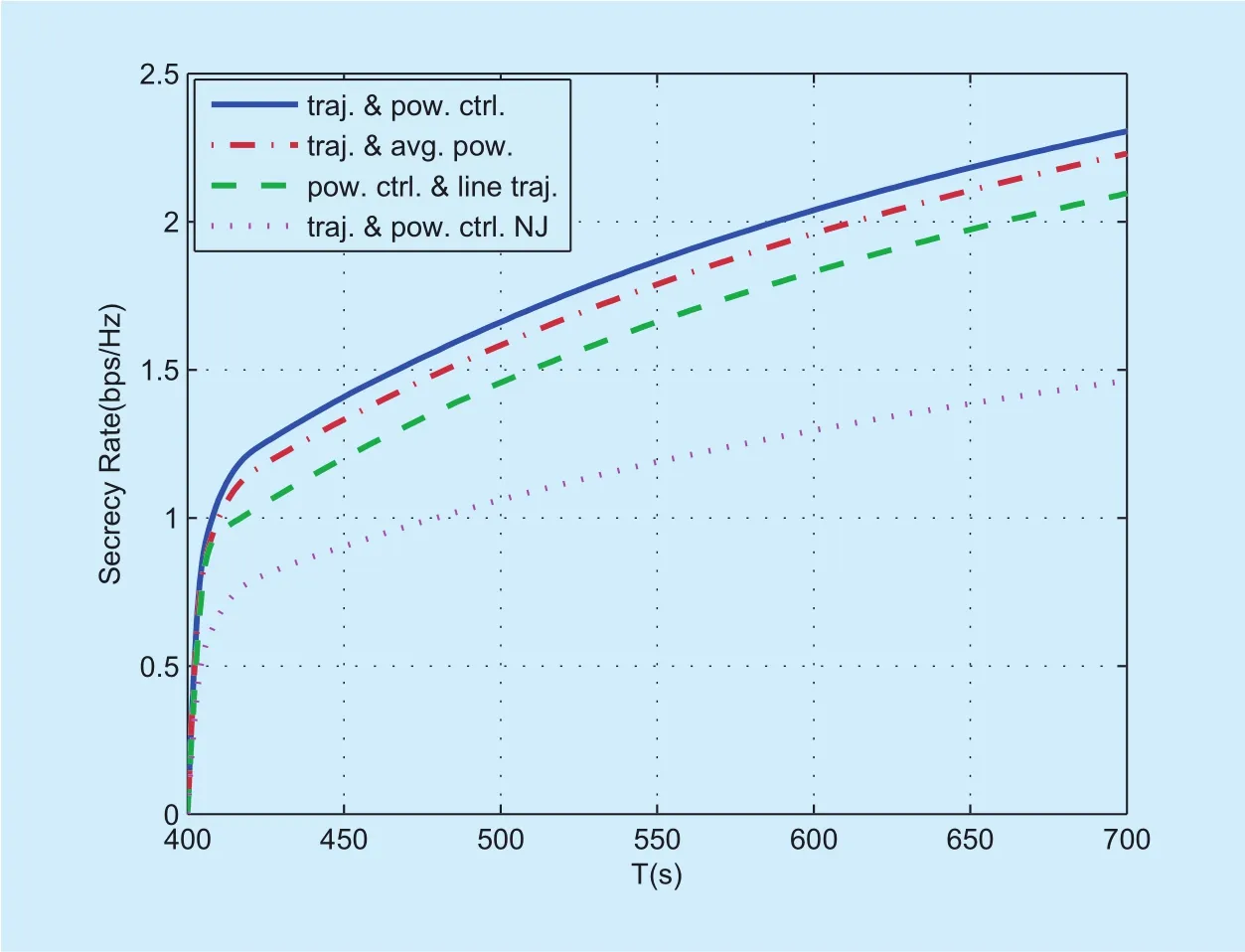
Fig. 3. Secrecy rate versus period T in case 1.

Figure 3 illustrates the average secrecy rates achievable as a function of period T for different algorithms. It is observed that the average secrecy rates of all algorithms monotonically increases as T gets larger. Regardless of the period T, the proposed “traj.& pow. ctrl.” outperforms the other three benchmark schemes while the benchmark “traj.& pow. ctrl. NJ” achieves the lowest secrecy rate. Such results indicates the cooperative jamming UAV is beneficial to significantly improve the achievable average secrecy rate performance of UAV-ground communications.Figure 4 shows the average secrecy rates of different algorithms versus the average jamming powerwhen=?5 dBm and 10dBm. It is observed that the secrecy rates of all algorithms except “traj. & pow. ctrl. NJ”first increase then decrease with the increase of. This is because for all algorithms except “traj. & pow. ctrl. NJ” too large jamming power will also increase the undesired interference to D, thus leading to the degrade of system secrecy performance. In particular,for the benchmark “traj. & avg. pow.” the secrecy rate sharply drops when＞0dBm because the equal jamming power in each slot is employed. The proposed “traj. & pow. ctrl.”algorithm always achieves the highest secrecy rate as expected. When=?5dBm, the benchmark “pow. ctrl. & line traj.” achieves higher secrecy rate than that of the benchmark“traj. & avg. pow.”, while when=10dBm,the latter achieves higher secrecy rate than the former when＜6dBm. Such results suggest that power control is more important for enhancing the achievable secrecy rate in the low S’s transmit power regime, while in the high S’s transmit power regime, trajectory design is more effective.

In figure 5, the average secrecy rates of the proposed algorithm are plotted versus the iteration number of Algorithm 1. Comparing the converged secrecy rate with the initial secrecy rate in figure 5, it is observed that joint trajectory and transmit power optimization enhances the achievable secrecy rate of mobile jamming system. It is also shown that Algorithm 1 is quite efficient as it converges in just a few iterations regardless of the period T.

Next, we consider Case 2. Figure 6 shows the trajectories of both UAVs by using different algorithms. Different from that in Case 1,the initial and final location of J are marked with □ and ?, respectively. It is observed that similar as the results in Case1, the trajectory of S for the proposed “traj. & pow. ctrl.” is closer to S with a closer hovering location than that for “traj. & pow. ctrl. NJ”. It can also be observed that J’s trajectory is quasi-odd symmetry with respect to S’s trajectories so as to degrade the eavesdropper’s channel as well as avoiding undesired interference to S. Besides,one can see that different from the results in Case 1, the trajectories for the proposed “traj.& pow. ctrl.” and the benchmark “traj. & avg.pow.” appear significant difference, especially when S (J) flies towards its final location.This is because for the proposed “traj. & pow.ctrl.”, S (J) is capable of deceasing the transmit power or even turn off the transmitter to avoid being eavesdropped (causing excessive interference to D) when S (J)flies along a relatively direct path towards thefinal location,while for the benchmark “traj. & avg. pow.”,since the equal power allocation is employed in each time slot, S (J) can only adjust its trajectory to be away from E (D) in order to prevent eavesdropping (interfering D), thus resulting in a longer arced path.

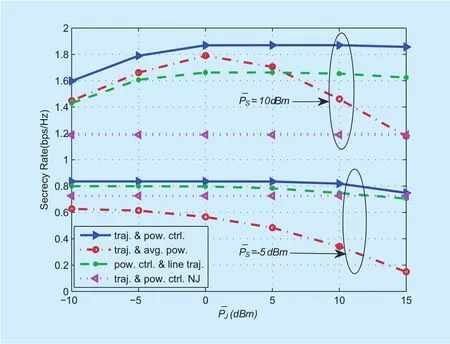
Fig. 4. Secrecy rate versus average jamming power in case 1.

Fig. 5. Convergence plot of Algorithm 1.

With such a UAV trajectory difference,Figure 7 plots a different secrecy rate performance of all the algorithms versus the period T from that shown in figure 3. Specifically,the secrecy rate gaps between the proposed“traj. & pow. ctrl.” and the benchmark “traj. &avg. pow.” is much larger than those in Case 1. In particular, “traj. & avg. pow.” achieves a lower secrecy rate than that for “traj. & pow.ctrl. NJ” when T ＜ 550s. This is because S (J)takes more time for a longer arced path which in turn resulting in a shorter hovering time,and do not utilize the transmit power efficiently. Such results validate that it is important and necessary to jointly optimize both UAVs’ trajectories and transmit power for UAV-ground communication with mobile jamming.

Fig. 6. Trajectories of UAV-enabled S and J in case 2.

Fig. 7. Secrecy rate versus period T in case 2.

V. CONCLUSION

In this paper, we investigate the secure UAV-ground communications with UAV-aided cooperative mobile jammer. Subject to both average and peak transmit power constraints as well as both UAVs’ mobility constraints, the average secrecy rate achievable is maximized by jointly optimizing both UAVs’ trajectories and transmit power over a given period. Based on the block coordinate descent and successive convex optimization methods, an iterative algorithm is proposed to solve the considered non-convex joint design problem. Simulation results demonstrate that the proposed UAV-aided mobile jamming strategy significantly outperforms the benchmark schemes.

ACKNOWLEDGEMENTS

This work was partly supported by National Natural Science Foundation of China (No.41504026, 61362009), Natural Science Foundation of Jiangxi (No.20152ACB21003),Foundation for Distinguished Young Talents Training Programme of Jiangxi(No.20171BCB23006).