Weizhi Zhong＊, Xiaoyi Lu Lei Xu Xin Liu

1 College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

2 China Dalian University of Technology, School of information and communications, Dalian 116024, China

Abstract: In order to solve the problem of inaccurate synchronization for distributed multiple-input multiple-output (MIMO) orthogonal frequency division multiplexing (OFDM)system in both multipath and low signal to noise ratio (SNR) channels, a golay pair aided timing synchronization (GPATS) method is proposed in this paper. A new synchronous training sequence based on the golay pair with guard interval is designed in GPATS method.By utilizing the unique properties of the new training sequence, the different timing point and the inter-transmitter delays (ITD) are obtained at the receiver. Simulation results show that, compared with the traditional synchronization approaches, the proposed algorithm can provide high accuracy in detecting different time offsets caused by the distributed transmitters of the MIMO-OFDM system, especially over multipath and low SNR channels.

Keywords: distributed MIMO-OFDM system;timing synchronization; golay pair; multipath;low SNR

I. INTRODUCTION

To enhance the channel capacity and transmission rate, MIMO-OFDM system has been proposed [1][2]. Utilizing the spatial and frequency multiplexing technique, the capacity and the transmission performance of the MIMO-OFDM system can be significantly improved; therefore it has become a promising candidate for 4G/5G [3-5]. There are two types of MIMO-OFDM system, centralized and distributed. For the centralized system,the antennas at the transmitter and the receiver side are placed very closely. Therefore, the signals from different transmitters arrive at the receivers simultaneously, and there is no inter-transmitter delay (ITD) exists. By contrast with the centralized system, the transmitters and receivers of the distributed system are placed in different geographical positions.Hence, the ITD has to be taken into account since different signals from different transmitters will be delayed and summed at the receivers. As comparing with the centralized system,the distributed system can achieve higher diversity gain, but it is much more sensitive to the synchronization error, therefore timing synchronization is the main problem to be solved in distributed MIMO-OFDM system.Various techniques have been proposed in the literatures to cope with this issue.

In [6-9], some researches have been suggested for MIMO-OFDM system to solve the timing synchronization problem. However,most of them are suitable for the centralized system. In these algorithms, the synchronization sequence (SS) is constructed by several repetitions of a synchronization pattern (SP).Since the SP for various transmitters has the same period, the methods are classified as the equal period synchronization pattern (EPSP).The methods can give good synchronization performance in centralized system, but in distributed system it is unable to find the ITDs and discriminate the signals from different transmitters. In [10], a training sequence for each transmit antenna in frequency domain is proposed. The method applies classes of orthogonal sequences to discriminate the transmit antennas. However, the problem of the algorithm is that the ITD must be less than the length of the cyclic pre fix (CP) of the training sequence, and it also assumes that the whole antenna does not exist the mutual frequency offset. To solve the problem, a typical timing synchronization method utilizing unequal period synchronization pattern (UPSP) is described in [11][12]. The idea of the UPSP method is to construct the SS for various transmitters with different periods, and thus,the algorithm enables the receiver to identify the time offsets from different transmitters individually. However, in practical systems,the ITDs are much smaller, and simulations results show that the UPSP method cannot afford correct estimation results in this situation.In the condition, a timing synchronization method with shift-orthogonal constant amplitude zero auto-correlation (CAZAC) method has been proposed [13-17]. In the method, the SS for various transmitters are constructed by weighted phase-shift CAZAC sequences, and then the ITDs can be easily found by the symmetrical correlation estimator at the receivers.However, the algorithm has two potential deficiencies, one is the in fluence of SNR and the other is the effect of multipath fading.However, in the case of multipath channels or poor SNR environment, the performance of the CAZAC method decreases rapidly.

In the literature [18], a common gray code sequence is used as synchronization sequence for single input and single output (SISO) system, but it is only suitable for SISO system.

To fill these research gaps, a novel golay pair aided timing synchronization (GPATS)method for distributed system is proposed in this contribution. Based on the golay pair, new synchronous training sequence with guard space is constructed. By utilizing the good correlation and anti-interference ability of the new training sequence, the ITDs can be easily found at the receiver and as demonstrated by the simulation results, the synchronization performance of the system in multipath and low SNR is greatly improved than CAZAC.

The rest of paper is organized as follows. In Section II, the distributed MIMO-OFDM system model is proposed, and the received non synchronous signal model is also formulated.In Section III, a brief overview of two typical synchronization methods is offered and the proposed novel GPATS algorithm is illustrated emphatically. In Section IV, the performance of the GPATS will be evaluated and compared to that of typical methods using UPSP and CAZAC. Finally conclusions are drawn in Section V.

In order to solve the problem of inaccurate synchronization for distributed multiple-input multiple-output (MIMO)orthogonal frequency division multiplexing(OFDM) system in both multipath and low signal to noise ratio (SNR) channels, a golay pair aided timing synchronization(GPATS) method is proposed in this paper.

II. SYSTEM MODEL

In this paper, a general distributed MIMO-OFDM system with Nttransmitters and Nrreceivers is considered. Besides, for ease analysis, the mobile station (MS) is assumed to use the centralized MIMO antenna, and the base station (BS) adopts the distributed antenna. The distributed MIMO-OFDM system model is described in figure 1. In the downlink case, it is considered that the times delays of the diverse transmitters are different.

The baseband samples of an OFDM symbol transmitted by the ith antenna can be given by

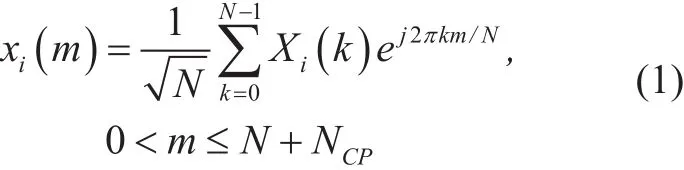
where Xi(k ) is the data in frequency domain before inverse fast Fourier transform (IFFT),N is the points number of IFFT and NCPdenotes the length of cyclic prefix (CP). The baseband samples received at the jth antenna of the receiver can be described as

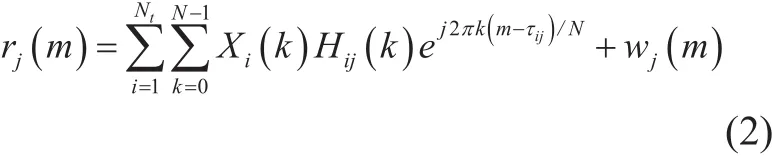
where Hij(k ) denotes the complex transfer function of the kth sub-carrier and the τijrepresents the time delay between the ith transmitter and the jth receiver. wj( m) is the additive white Gaussian noise (AWGN) with zero mean value and variance of

III. TIMING SYNCHRONIZATION METHOD FOR DISTRIBUTED MIMOOFDM SYSTEM

3.1 Review of the typical synchronization methods

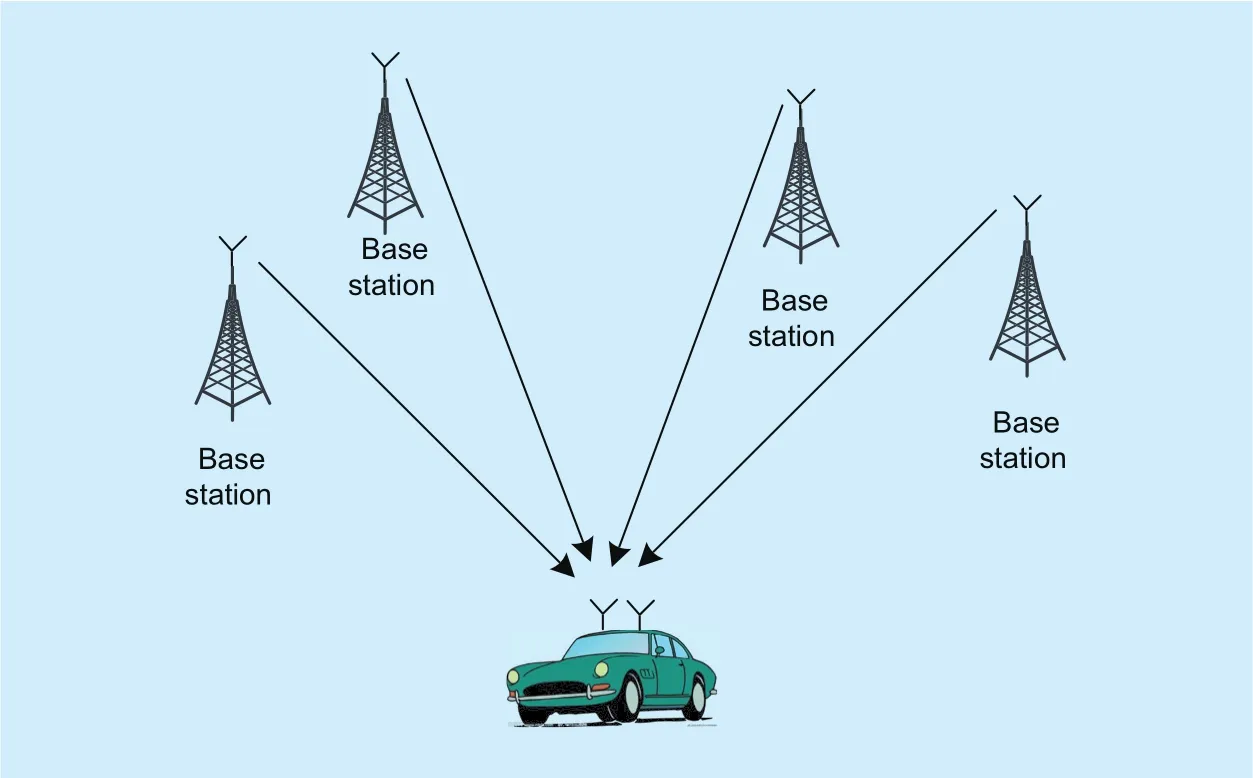
Fig. 1. The model of the distributed MIMO-OFDM system.

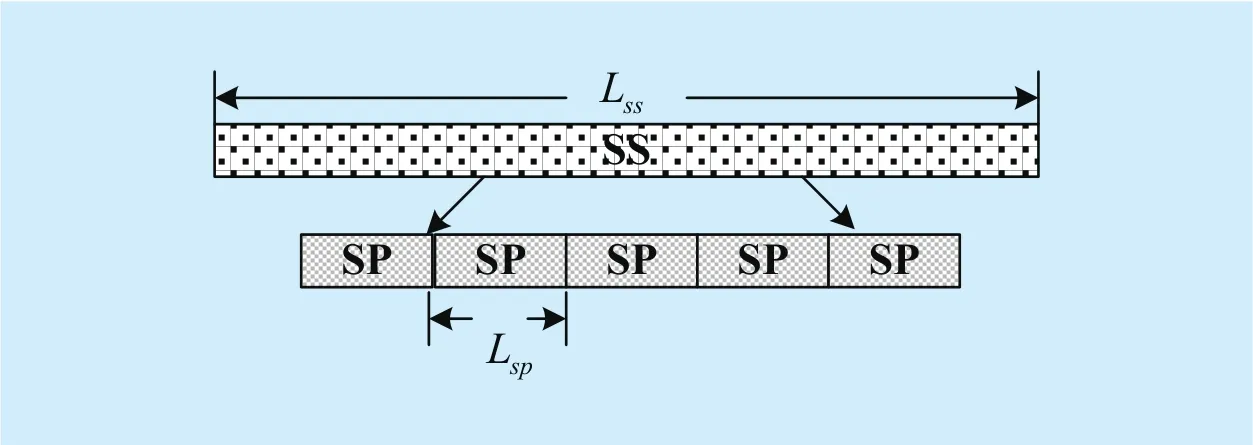
Fig. 2. The structure of the SS.

In this section, two typical timing synchronization methods for distributed MIMO-OFDM system will be briefly introduced, which are the UPSP and CAZAC. For simplicity, a system with two-transmitter and only one-receiver will be adopted in this work. The preamble at the beginning of the frame contains a SS with length Lss. Additionally, the SS is constituted by several repetitions of a shorter synchronization pattern (SP) with length Lsp. The structure of the SS of the two methods used in this contribution is described in Fig 2.

1) UPSP Synchronization Method

UPSP is a kind of synchronization method for distributed MIMO-OFDM system, the idea of UPSP is to design the synchronization sequences for various transmitters with different periods, and thus it enables the receiver to achieve the time offsets from different transmitters individually.

In UPSP, a unique Lspvalue is assigned for each individual transmitter when constructing the synchronization sequences. The SS should be designed as follows.

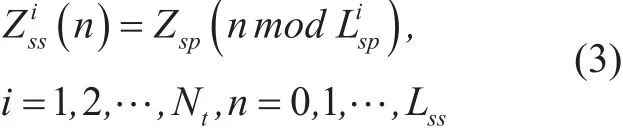
At the receiver, Ntcorrelators are required to find the time offset τifor each individual transmitter. Hence, the estimation valuecan be given by

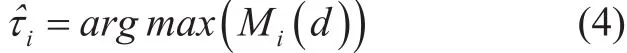
and

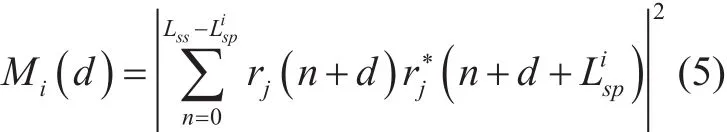
where, rj( n) is the received signal of the jth receiver. From equation (5) we can find that,when the receiving end uses theto carry on the correlation operation, only the SS sent by the ith transmitter will contribute to the correlation peak, hence the time offset for the ith transmitter can be found. Moreover, the SS from other transmitters do not generate peaks,because they have different periodicity.

However, in practical MIMO-OFDM systems, when the ITDs is smaller than several decades of samples, due to the interference between the different transmitters, the UPSP method cannot distinguish the right time offset.

2) CAZAC Synchronization Method

In order to overcome the shortcomings of the UPSP algorithm, the CAZAC sequence based synchronization method is proposed to estimate the time offset and detect the ITDs for distributed MIMO-OFDM systems. In the method, the SS assigned for various transmitters are constructed by CAZAC sequence.Since the sequences has good correlation and pseudo reflexive characteristics, the good time offset can be provided by only one symmetrical correlator at the receiver.

The CAZAC sequence is defined as follows

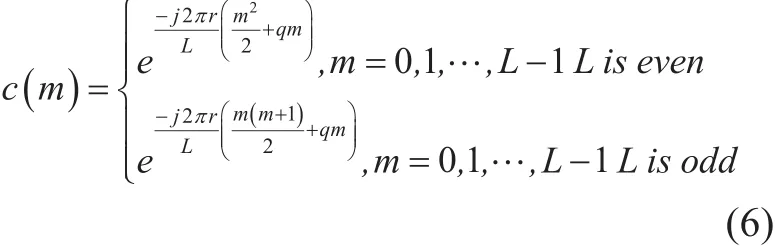
In the formula (6), L denotes the sequence length, q is an arbitrary integer, r and L are the prime numbers respectively. The autocorrelation of the CAZAC sequence is an ideal two valued function, which can be described as

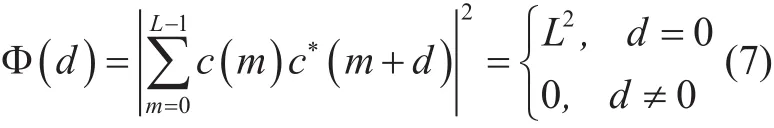
It can be proved by the definition of the CAZAC sequence, when the q equal to zero,the sequence has pseudo reflexive characteristics, that is

Fig. 3. The structure of the SS in the UPSP algorithm.

According to the characteristics of the CAZAC sequence described above, the synchronization sequence for the ith transmitter is designed as follow

where ωidenotes the orthogonal weighted factor, and Diis the cyclic shift length of the ith transmitter antenna. c (mod(k + Di)N)stands for the CAZAC sequence which is cyclically shifted with Di. Since Diis unique for each transmitter, the synchronization sequence xi,kassociated with the ith transmitter is different.

At the jth receiver, the correlation results of the SS from the ith transmitter should meet a pulse function, which can be described as follow

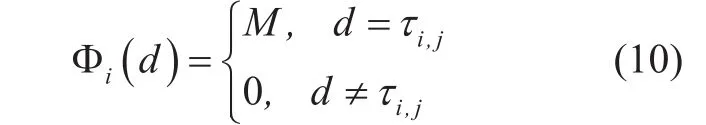
where M is a real number, and τijis the time offset between the ith transmitter and jth receiver. Because of the optimal auto-correlation property of the CAZAC sequence, the good correlation performance of the synchronization sequence can be guaranteed.

At the jth receiver, only one estimator is needed to identify the time offsets from various transmitters. Therefore, the time offsets can be given by

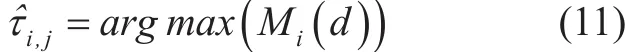
where

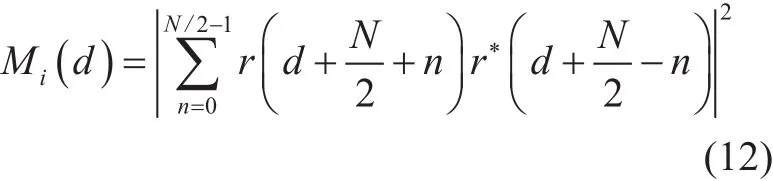
Owing to the self-invertible property and the good auto-correlation characteristic of the CAZAC sequence, the output of the correlator contains Ntpulses, each of which represents the starting point of the corresponding transmitter. As a result, the time offset can be found immediately, and the ITDs between different transmitters can be expressed as

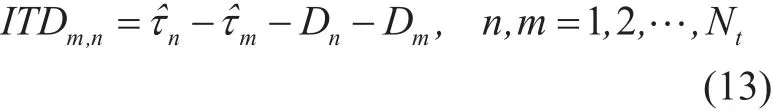
where ITDm,nrepresents the ITD between the mth transmitter and nth transmitter.

The CAZAC based time synchronization method can effectively obtain the time offsets for different transmitters. However, in poor SNR conditions and in a multipath environment, synchronization performance of the method degrades sharply.

3.2 Proposed novel synchronization method

In order to solve the problem of the typical UPSP and CAZAC synchronization algorithm,a novel GPATS method is proposed in this paper. In this section, the golay complementary pair (GCP) is presented first. Then, based on the golay pair, a kind of synchronous training sequence (SP) with guard space is constructed.Based on the designed SP, a novel synchronization algorithm is proposed.

1) Golay Complementary Pair

The sequence A and B are assumed to be the golay complementary pair, which can be given as[19]

where, akand bkare the kth value of the sequence A and B respectively, and N=2nis the length of the sequence. n = 1,2 ,……. In practice, the non-periodic autocorrelation of the sequence A and B has the following characteristics

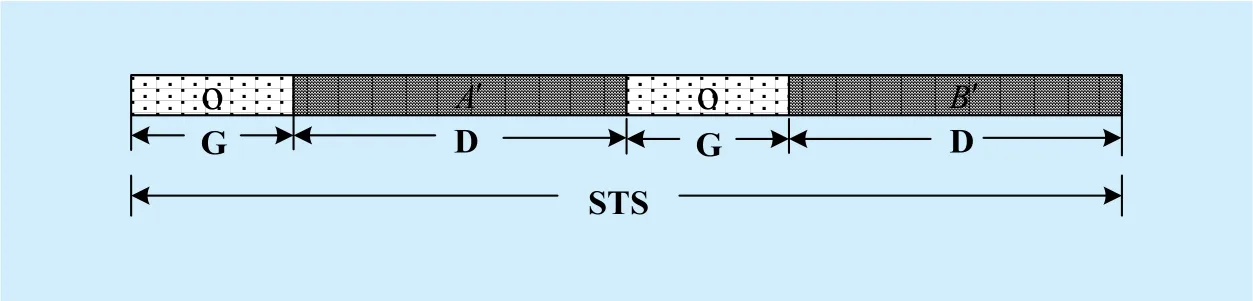
Fig. 4. The designed STS pattern adopts GCP and guard space.

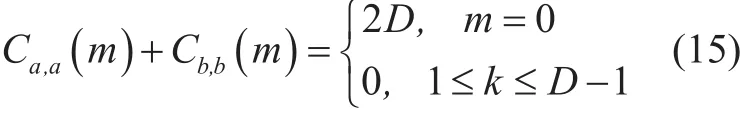
where Ca,a(m) and Cb,b(m ) denote the non-periodic autocorrelation of the A and B respectively, and they can be defined as

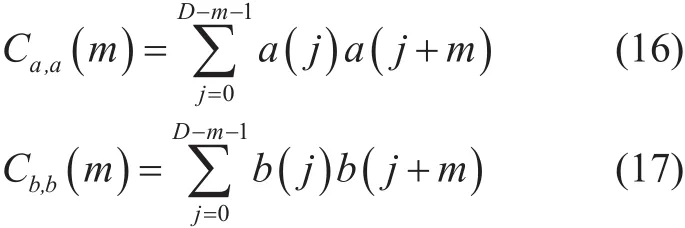
2) Novel Synchronous Training Sequence

The traditional synchronous training sequence (STS) is composed of pseudorandom noise sequence (PNS) or CAZAC sequence, in this contribution, a novel STS adopts GCP and uses guard space will be designed [20]. The STS pattern is depicted in figure 4

where O is the guard interval of the A′ and B′, and the values of it are zeros. G is the length of O, and it must be greater than the channel extension. A′ and B′ are novel GCP,which are constructed by A and B, and they can be expressed as follow

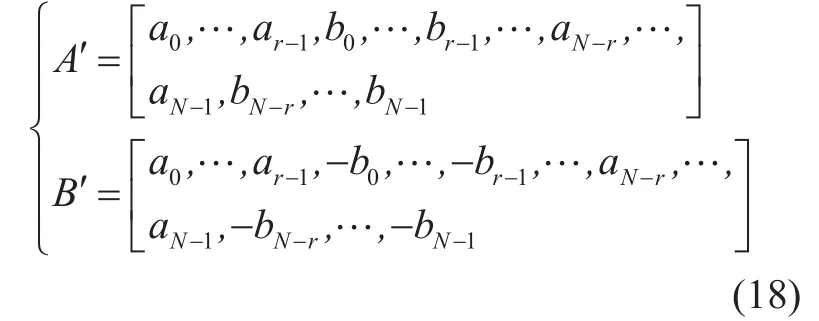
It has been proved that, A′ and B′ are also have better correlation properties, and the length of them areflexible. As the existence of the protection interval O and the good autocorrelation characteristics of the A′ and B′, the synchronization algorithm using novel STS can be used in the multipath and low SNR channels to effectively carry out the time point localization.

3) Proposed GPATS Method

In the proposed GPATS method, the STS sent by the transmitters are designed as figure 4. At the receiving end, the calculation of the correlation are respectively operated between the received data and the A′ and B′. The results of non-periodic auto-correlation are shown as follows

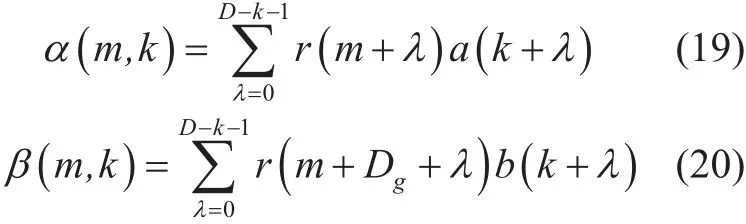
where r( m) represents for the mth received sample, a( k) and b( k) are the kth item of the sequence A′ and B′ respectively, and Dg= D+ G . γ(m,k) is the sum of α(m,k)and β(m,k), which can be expressed as follow

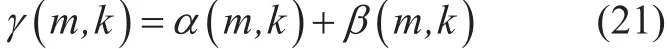
Then the estimation value of the timing offset can be given by

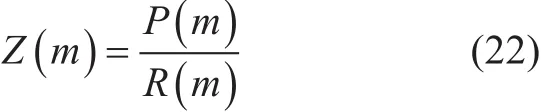
where

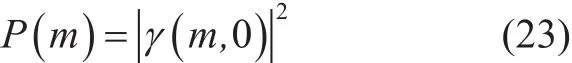
and

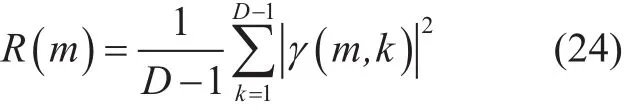
The sampling position corresponding to the maximum value of the Z( m) is the position of the timing synchronization, and the symbol timing offset can be approximated as follow

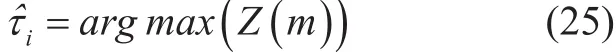
In the condition, the optimal time offset can be provided, which can be defined as

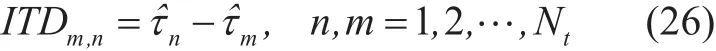
where ITDm,nrepresents the ITD between the mth transmitter and nth transmitter.

The difference between the proposed method and the classical algorithms is that, the UPSP and CAZAC based synchronous algorithm uses the signal energy normalization to suppress the noise and the multipath fading.However, the proposed method utilizes the non-periodic autocorrelation complementary characteristics of the golay pairs, and obtains the sharp peaks by calculating the ratio between the amplified signal energy and the averaged signal power in the auto-correlation complementary region. In addition, the protection interval can be easily loaded in the golay complementary pairs, and this kind of synchronization sequence with a protective interval can effectively restrain the multipath interference, however, this mode of loading in the UPSP and CAZAC sequence design is difficult to achieve. The theoretical results prove that the proposed method implements the timing synchronization more effectively than the traditional algorithms in low SNR and multipath fading environment.

IV. SIMULATION RESULTS

In this section, the performance of the proposed GPATS timing synchronization approach will be demonstrated when communication in distributed MIMO-OFDM system.The performance of the typical UPSP and CAZAC algorithm will also be simulated and used as comparison objects.

Without loss of generality, the STS structures of the UPSP and CAZAC described in figure 2 and figure 3 will be used for simulations, and the STS structure of the GPATS method shown in figure 4 will be adopted in this section. The simulation parameters are contained in Table.1 and Table.2. Using theparameters listed in Table.1, the ITDs of the UPSP, CAZAC and the proposed GPATS in single-path scenario are displayed in figure 5(a), Fig6(a) and figure 7(a) respectively, and the performances of the three methods in multipath condition are investigated in figure 5(b),Figure 6(b) and figure 7(b) respectively. The distributed MIMO-OFDM system employing two-transmitters and one-receiver is applied in the simulation. The ITD is set to be 100, which means the delay between two transmitters is 100. When in multipath conditions, the time delay of the lth path from the ith transmitter to the jth receiver is τl,ij, and τ1,ij=0, τ2,ij=10,τ3,ij=20, τ4,ij=30, τ5,ij=40. The amplitude of the lth path is al,ij, and a1,ij=1, a2,ij=0.8,a3,ij=0.6, a4,ij=0.4, a5,ij=0.2.

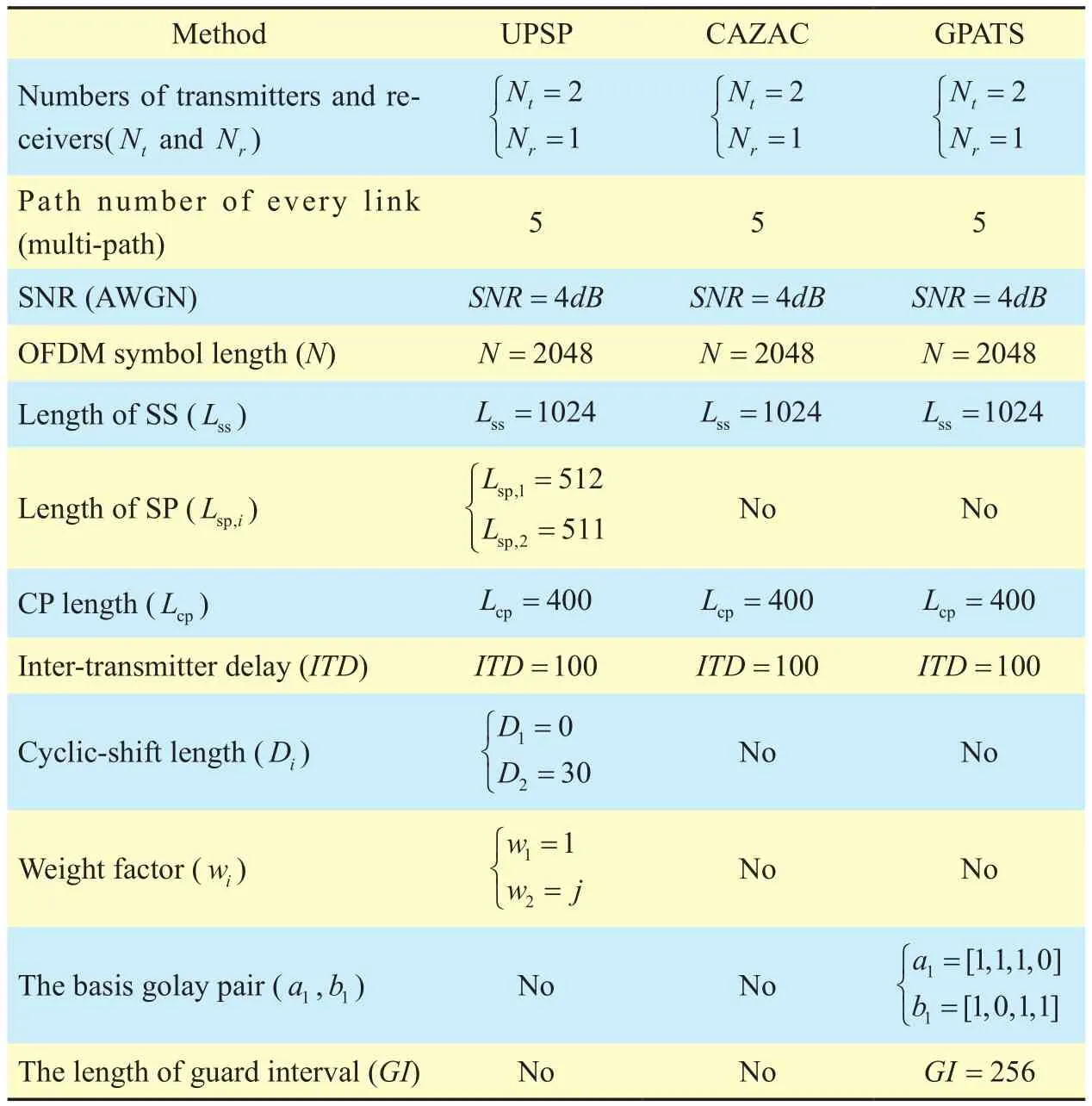
Table I. Parameters of simulation in single-path / multipath environment.

As shown in figure 5(a), in single-path environment, the UPSP can give a clear spike to locate the start of the synchronization sequence at the receiver, and the distance between the correlation peaks, which represents the time delay of the two transmitters can be easily found. As observed in figure 5(a), the ITD value of the UPSP approximates to 107 which is close to the real value 100. However,as shown in figure 5(b), in multi-path environment, due to the presence of the multipath interference, the UPSP has the phenomenon of ambiguous peak. In other words, all of these peaks have equal chance to be recognized as the start points.

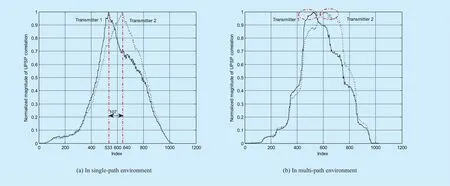
Fig. 5. The performance of the ITD recognition using UPSP.

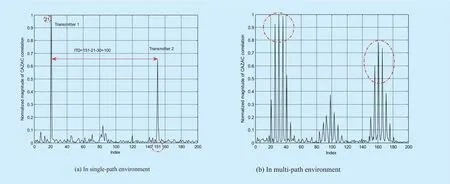
Fig. 6. The performance of the ITD recognition using CAZAC.

Fig. 7. The performance of the ITD recognition using GPATS.

Thus the UPSP is not able to distinguish the start of the different transmitters in multi-path condition and the accuracy value of the ITD can’t be obtained. The performance of the ITD recognition adopted CAZAC method in single-path environment is shown in figure 6(a).The simulation results show that the CAZAC based method can obtain two sharp pulses which represent the start points of the two transmitters. As presented in the figure 6(a),the distance of the two pluses is 130 and the value of ITD can be clearly identified as 100.However, as shown in figure 6(b), in multipath conditions, due to the existing of multipath interference, the CAZAC based method has a number of peaks, thus the starting point of the synchronization sequence can’t be separated which leads to the poor estimation accuracy of the ITD values. Comparing to the previous two methods, the performance of the proposed GPATS algorithm is much better in multi-path environment. As shown in figure 7(b), the two largest correlation peaks which represent the start points of the two transmitters, belong to the direct link; While the other peaks which are much smaller, belong to the multi-paths. The distance of the two largest pluses can be clearly identified as 100 and the value of ITD is 100.

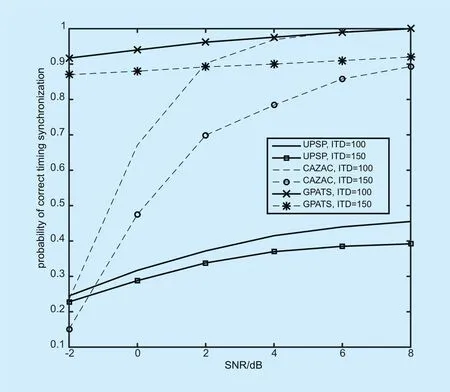
Fig. 8. The performance comparison of the three algorithms in single-path environment.

The figure 8 and figure 9 are presented to demonstrate the performance of the three al-gorithms in both single-path and multi-path environments. The simulation parameters are shown in Tabel.2.

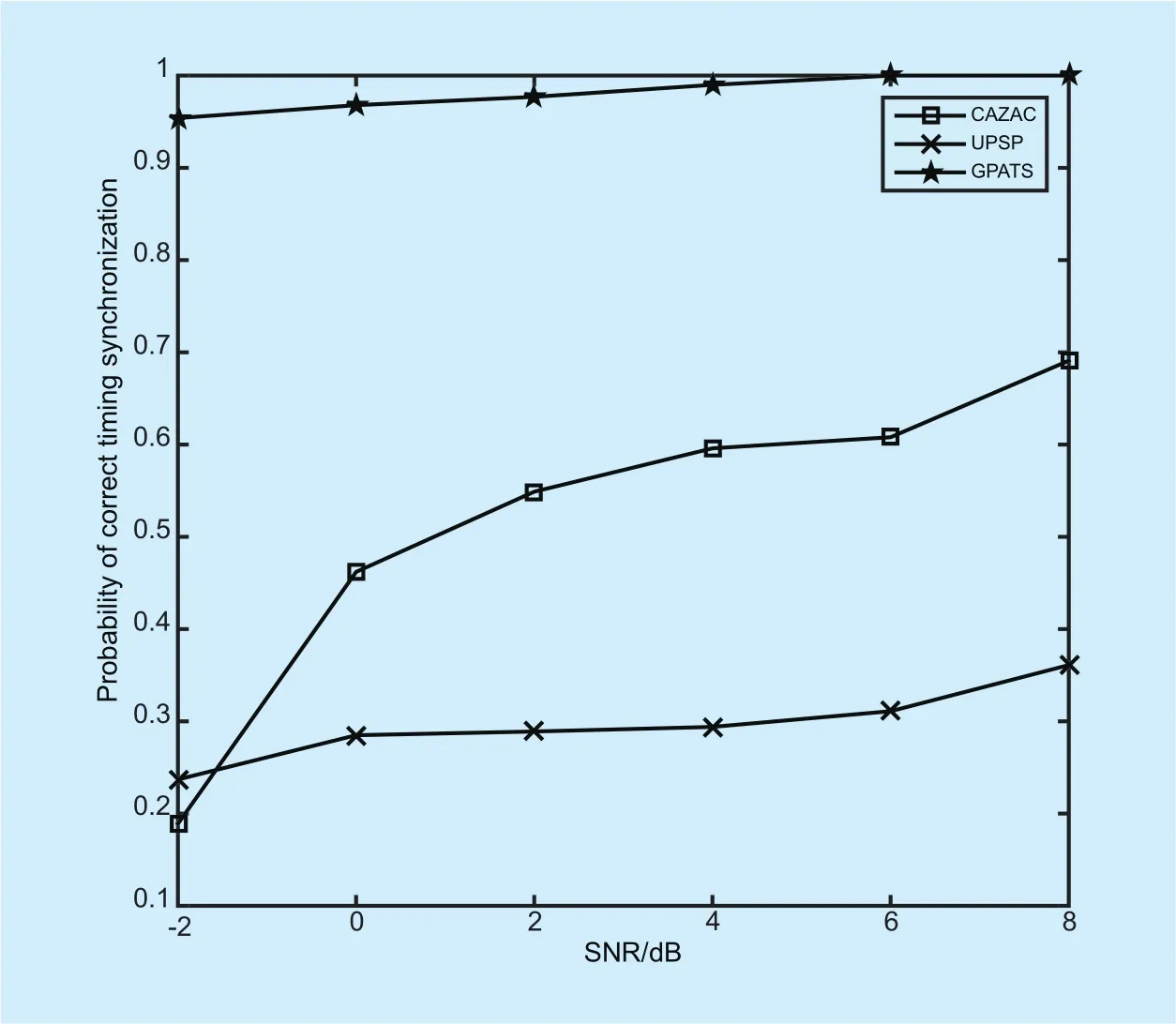
Fig. 9. The performance comparison of the three algorithms in multi-path environment.

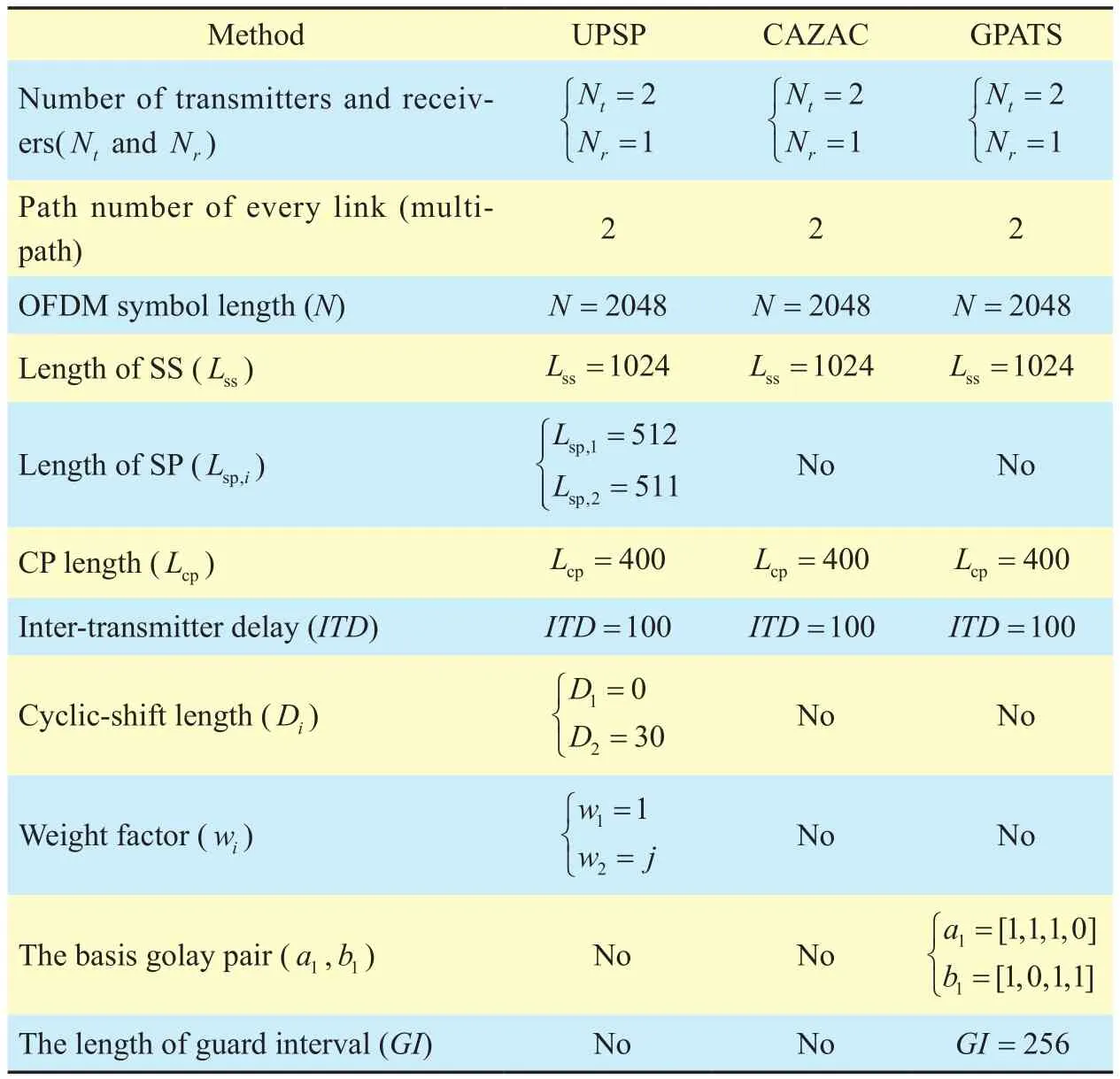
Table II. Parameters of simulation in single-path / multipath environment

As verified by figure 8 and figure 9, upon invoking the new golay synchronous training sequence and the guard interval, the proposed GPATS method has better performance than the other two algorithms, especially in low SNR and multi-path environment, and the proposed algorithm is only applicable to the multi-path case with LOS.

V. CONCLUSION

In this paper, a distributed MIMO-OFDM system was considered, and the design of timing synchronization algorithms was investigated. First, the golay complementary pair was introduced, and based on the pair a novel synchronous training sequence was designed.Then, using the novel synchronous training sequence, a GPATS method that efficiently improved the synchronization performance in both low SNR and multi-path environment was proposed. The performance of the proposed method was evaluated and the simulation results showed that in low SNR and multi-path channels, the GPATS method can provide high accuracy in detecting different time offsets caused by the distributed transmitters of the MIMO-OFDM system.

ACKNOWLEDGEMENTS

This work was supported by the Fundamental Research Funds for the Central Universities(NS2017066).