福建省廈門大學(xué)附屬實驗中學(xué)(363123) 林運來

題目已知拋物線C∶y2=2px經(jīng)過點P(1,2),過點Q(0,1)的直線l與拋物線C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N.

(I)求直線l的斜率的取值范圍;

(II)設(shè)O為原點,求證：為定值.

解析(I)由已知得4=2p,解得p=2,所以拋物線C的方程為y2=4x.設(shè)A(x1,y1),B(x2,y2),直線l的斜率存在且不為0,設(shè)其方程為y=kx+1(0),由得即ky2-4y+4=0.由已知,得?=16-16k＞0,解得k＜1 且0.又因為直線PA,PB與y軸相交,故l不過點(1,-2),從而3.所以直線l的斜率的取值范圍是(-∞,-3)∪(-3,0)∪(0,1).

(II)解法1 由(I)可知y1+y2=y1y2=因為A,B均在拋物線上,所以又因為直線PA,PB均與y軸相交,所以直線PA,PB的斜率均存在,即y12,y22.因為所以直線PA的方程為令x=0,解得所以可知所以同理可得所以

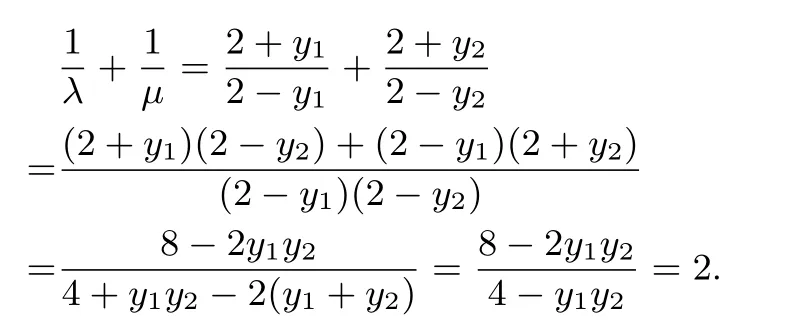
解法2 由(I)得(kx+1)2=4x,即k2x2+(2k-4)x+1=0,因為k20,所以

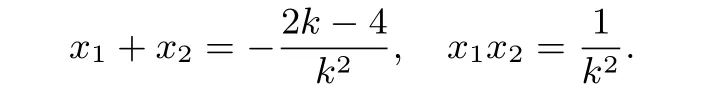
又因為直線PA,PB均與y軸相交,所以直線PA,PB的斜率均存在,即知x11,x21.因為kP A=所以直線PA的方程為令x=0,解得y=所以由λ--→QO,可知所以同理可得所以

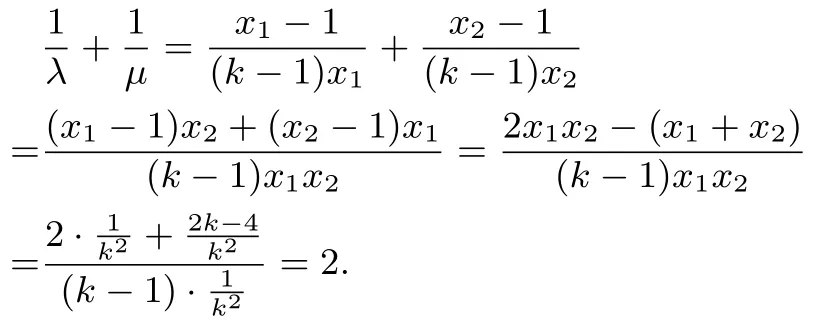
推論1 拋物線C∶y2=2px(p＞0)在點P(x0,y0)處的切線與y軸交于點Q,過點Q的直線l與拋物線C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N,O為原點,則為定值2.

證明拋物線C∶y2=2px(p＞0)在點P(x0,y0)處的切線PQ的方程為y0y=p(x+x0),由已知得x0y00,且設(shè)A(x1,y1),B(x2,y2),直線l顯然不能與x軸垂直,設(shè)其方程為聯(lián)立消去x,得即ky2-2py+py0=0,由已知得所以因為A,B均在拋物線上,所以又因為直線PA,PB均與y軸相交,所以直線PA,PB的斜率均存在,即y10,y20.因為所以直線PA的方程為令x=0,解 得所以由可知所以

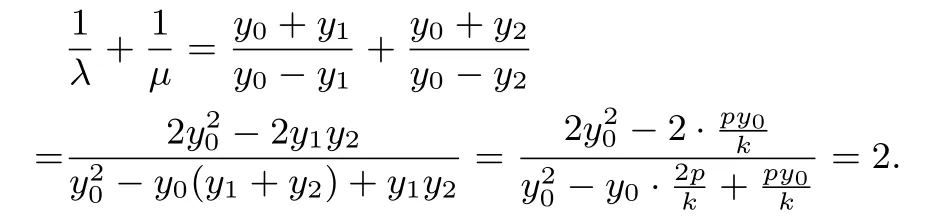
推論2 橢圓在點P(x0,y0)處的切線與y軸交于點Q,過點Q的直線l與橢圓C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N,O為原點,則為定值

證明橢圓在點P(x0,y0)處的切線PQ的方程為由已知得x0y00,且Q設(shè)A(x1,y1),B(x2,y2),直線l顯然不能與x軸垂直,設(shè)其方程為y=kx+聯(lián)立消去y得：整理得所以?＞0,且

又因為直線PA,PB均與y軸相交,所以直線PA,PB的斜率均存在,即x10,x20.因為

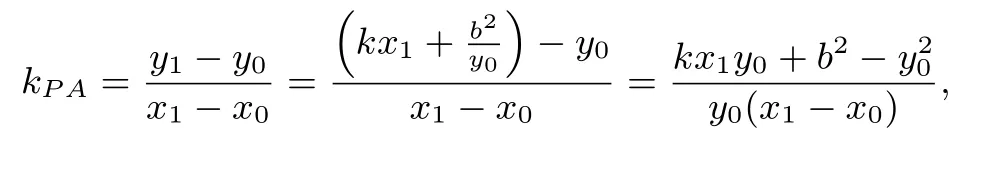
所以直線PA的方程為x0),令x=0,解 得所以由得所 以同理可得所以

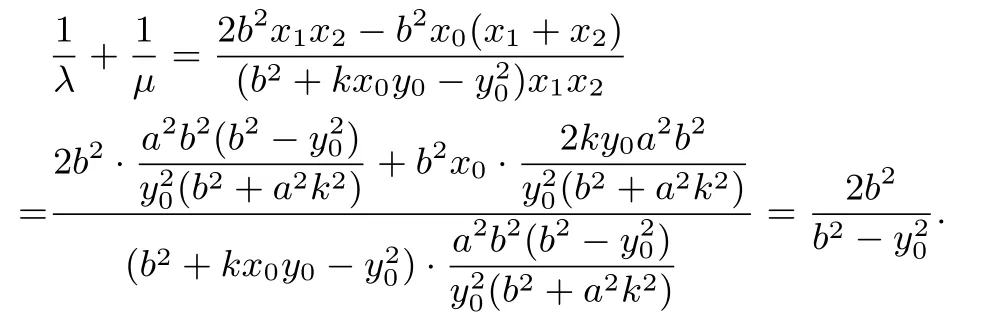
推論3 圓C∶x2+y2=r2在點P(x0,y0)處的切線與y軸交于點Q,過點Q的直線l與圓C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N,O為原點,則為定值

推論4 雙曲線=1(a＞0,b＞0)在點P(x0,y0)處的切線與y軸交于點Q,過點Q的直線l與雙曲線C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N,O為原點,則為定值

推論3 及推論4 可以類比推論2 進(jìn)行證明,此處不再贅述.