Jing Zhang, Yanhui Zhai ?, Deyu LiSchool of Foreign Language, Shanxi University, Taiyuan 030006, Shanxi, People’s Republic of China

2Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, School of Computer and Information Technology, Shanxi University, Taiyuan 030006, Shanxi, People’s Republic of China

Abstract: Fuzzy decision implication is an extension of decision implication in the fuzzy setting, serving to uncover the dependencies of fuzzy attributes. This study presents the interpretation of fuzzy decision implication in the fuzzy decision context. Specially, they will show that from fuzzy decision contexts one can obtain a closed fuzzy set of fuzzy decision implications, and the semantical characteristic of the obtained fuzzy set can be interpreted by fuzzy decision context and can be represented by some operators of fuzzy decision context. Conversely, starting from a fuzzy set of fuzzy decision implications, they can form a fuzzy decision context, from which the given fuzzy set can be derived. The result actually implies that they have constructed a correspondence between closed fuzzy sets of fuzzy decision implications and fuzzy decision contexts, and thus shows the equivalence of two interpretations of fuzzy decision implications.

1 Introduction

Decision-making is of importance in all science-based professions,where specialists apply their knowledge to make valuable decisions.This kind of knowledge can be captured by a decision implication A ?B, a term in formal concept analysis [1–5], expressing that when all conditions in A occur, one should take the decisions in B [6–10].

Similar to attribute implications [1, 11], the logical study of decision implications can be divided into two parts [7], the semantical aspect and the syntactical aspect. The semantical aspect accounts for the following questions on decision implications:

· The soundness of decision implications: how to determine whether a decision implication is valid?

· Redundancy of decision implications: does there exists a decision implication that can be deduced from the other decision implications?

· Completeness of decision implications: how to obtain a compact set of valid decision implications from the given set of decision implications without loss of information?

· Decision implication basis[8–10]:how to derive a non-redundant complete set of decision implications?

In the syntactical aspect, one starts with a set of decision implications and some inference rules [6, 12], and then deduce new decision implications from the given set by repeatedly applying some inference rules. This process brings forth the following questions concerning the semantical aspect:

· The soundness of inference rules: is any deduced decision implication valid, provided that any decision implication taken from the given set is valid?

· Completeness of inference rules:when the given set is complete,can one obtain all valid decision implications only by repeatedly applying some inference rules?

· Redundancy of inference rules:can one obtain one inference rule from the others?

Considering fuzzy values also existing in real datasets,Zhai et al.extended decision implication to fuzzy decision implication and presented its semantical and syntactical aspects [13]. By means of the results of [13], Zhai et al. [14] proposed fuzzy decision implication canonical basis and proved that the canonical basis is complete, non-redundant and contains the least number of fuzzy decision implications among all complete sets of fuzzy decision implications, just as canonical basis with respect to attribute implications [1] and decision implication canonical basis with respect to decision implications [8, 9]. Thus, a fuzzy decision implication canonical basis can be regarded as the most compact set of decision information without any information loss.

All the results, however, were obtained in a logical way and are not applied to data tables. Though the logical studies of fuzzy decision implications have provided a deep and theoretical insight into fuzzy decision implications, the studies of fuzzy decision implications with respect to data tables can link the properties of data tables with fuzzy decision implications and provide a practical insight into fuzzy decision implications [15]. Thus, this study aims to provide an interpretation of fuzzy decision implications within data tables, i.e. fuzzy decision contexts. We will show how to derive fuzzy decision implications from a fuzzy decision context and describe how to connect fuzzy decision implications with a fuzzy decision context. The results actually imply the equivalence of two interpretations of fuzzy decision implications, i.e. the logical way and the data-driven way.

This paper will be organised as follows. Section 2 provides an overview of basic notions, in particular, some basic properties of a complete residuated lattice. We will introduce fuzzy decision implications and fuzzy decision contexts in Section 3. Afterwards,we connect fuzzy decision implications with fuzzy decision contexts in Sections 4 and 5. Section 6 concludes the paper and presents some further work.

2 Preliminaries

A complete residuated lattice [16] is an algebra(L, ∧, ∨, ?, →,0,1) such that

(i)(L, ∧, ∨,0,1)is a complete lattice with 0 and 1 being the least and greatest elements of L, respectively;

(ii)?is commutative,associative,and a ?1=1 ?a=a,for each a ∈L;

(iii)?and →satisfy the adjointness property:a ?b ≤c if and only if a ≤b →c, for each a, b, c ∈L.

A truth-stressing hedge (hedge for short):?:L →L such that for each a,b ∈L, 1?=1, a?≤a, (a →b)?≤a?→b?and a??=a?.

As for hedges, two commonly used ones are

(i) Identity, i.e. for each a ∈L, a?=a.

(ii) Globalisation, i.e.

Several properties of the residuated lattice are listed here for later use; for a,b,c,yi∈L, we have

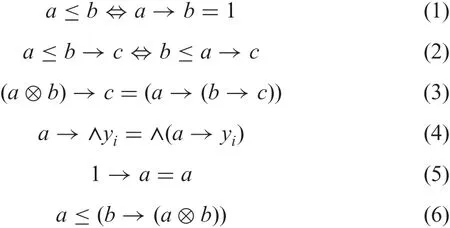
As a special case of complete residuated lattice, L=[0,1] is commonly used, with 0 and 1 being the least and greatest elements,respectively, and ∧ and ∨ being minimum and maximum,respectively.Several important pairs of adjoint operators are

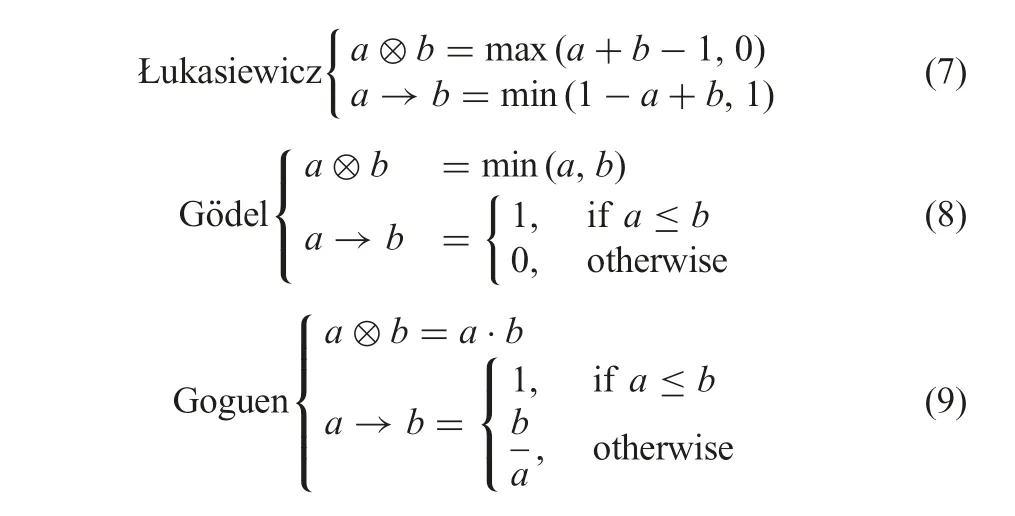
With L being the structure of truth degrees,we define a fuzzy set A(or L-set) as a mapping from a universe U to L,A:U →L,whose value A(u) is the degree to which u is contained in A. As usual, we also denote a fuzzy set A bywhere ai=A(ui). By, we denote the set of all L-sets in U. Several useful operators can be defined for L-sets A and B accordingly,such as

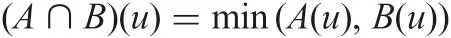
and

Other notions can, therefore, be adopted based on the two above operators; e.g. we say A ?B if, for each u ∈U, we have A(u)≤B(u). For a ∈L and A ∈LU, two special L-sets are given by a ?A and a →A with (a ?A)(u)=a ?A(u) and(a →A)(u)=a →A(u).

As an extension of the classical subset-hood relation ?, the subset-hood degree is given by

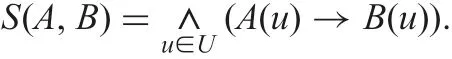
3 Fuzzy decision implications and fuzzy decision context

In this section, we will recall some basic notions and present some results of fuzzy decision implications and a fuzzy decision context[13, 14].

3.1 Fuzzy decision implications

Let C,D be two finite universes and LC,LDbe two systems of L-sets in C and D,respectively.A fuzzy decision implication on C and D is of the expression A ?B,where A ∈LCand B ∈LD.Here A is the premise of the implication and B the consequence of the implication.All fuzzy decision implications on C and D are denoted by I.

For a fuzzy set T ∈LC∪D,the degree to which T respects A ?B is defined by

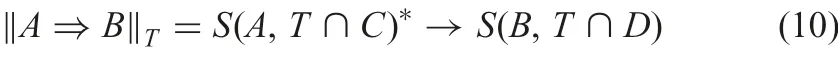
where * is a hedge. The degree to which A ?B holds in a set T ={T1,T2, ...,Tn} is defined by

For a fuzzy set L of fuzzy decision implications,the set of models of L is given by

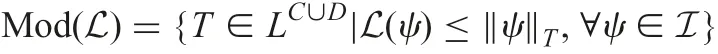
where L(ψ) is the membership degree of ψ in the fuzzy set L.Then the degree to which A ?B semantically follows from L is defined by

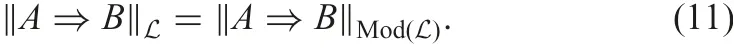
A fuzzy set L of fuzzy decision implications is closed if, for each A ?B, we have ‖A ?B‖L=L(A ?B). A fuzzy set D ?L is complete with respect to a closed fuzzy set L, if we have‖A ?B‖D=‖A ?B‖L, for each A ?B. A fuzzy set D ?L is non-redundant if no proper subset of D is complete with respect to L.

3.2 Fuzzy decision context

In this subsection, we will introduce a fuzzy decision context as an extension of the decision context under the setting of fuzzy attributes.

Definition 1:Given a complete residuated lattice L,a fuzzy decision context is a quadruple K =(G,C,D,I),where G is a set of objects,C is a set of condition attributes, D is a set of decision attributes and I =IC∪IDwith ICassigning a degree IC(g,m)∈L to g ∈G and m ∈C, and IDassigning a degree ID(g,m)∈L to g ∈G and m ∈D.

Example 1: An illustrative example is presented in Table 1, where

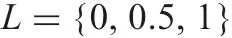
G ={Mercury,Venus,Earth,Mars,Jupiter,Saturn,

Uranus,Neptune,Pluto}

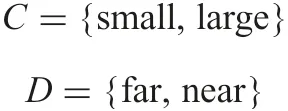
and entries indicate the degrees to which objects have attributes.Forinstance, IC(Uranus,small)=0.5 says that the degree to which Uranus is small is equal to 0.5, while IC(Uranus,large)=0.5 says that the degree to which Uranus is large is also equal to 0.5, which means that Uranus is not so small and is not so large either.

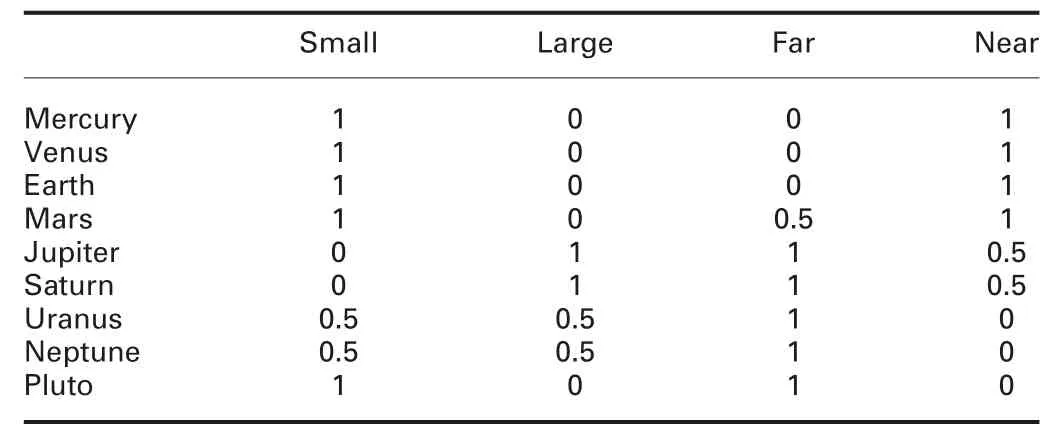
Table 1 Fuzzy decision context

Given a hedge *, the following notations from [13] are used in the study: for A ∈LGand m ∈C

and, for A ∈LGand m ∈D

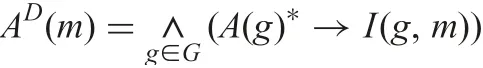
and, for B ∈LCand g ∈G

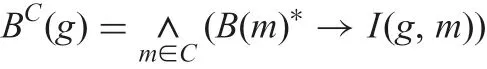
and, for B ∈LDand g ∈G

In the sequel, for g ∈G, we use Cg∈LCand Dg∈LDto denote the fuzzy sets IC(g,m), m ∈C and ID(g,m), m ∈D, respectively.Now, we introduce *-consistent fuzzy decision contexts.

Definition 2: A fuzzy decision context is *-consistent if for any g,h ∈G, we have S(Cg,Ch)?≤S(Dg,Dh), where?is a hedge.

This limitation in Definition 2 ensures that stronger conditionswill produce stronger consequencesThis will be clearer when Definition 2 degenerates to the crisp case. Recall that in the crisp case, a decision context is consistent[6] if for any g, h ∈G, Cg=Chimplies Dg=Dh. Observe that the condition of *-consistent is an extension of consistent.In fact, Cg=Chyields S(Cg,Ch)=1 and S(Ch,Cg)?=1, which implies S(Dg,Dh)=1. Thus, we have Dg?Dh, Dg?Dh, and Dg=Dh.

Example 2:Table 1 is not*-consistent for any hedge*since,for the objects, Mercury and Pluto, we have S({1/small,0/large},{1/small,0/large})?=1 but S({0/far,1/near},{1/far,0/near})=0 →1 ∧1 →0=0.

4 From fuzzy decision context to fuzzy decision implication

Now we show how to extract fuzzy decision implications from fuzzy decision contexts.

Definition 3: A fuzzy decision implication A ?B holds in K =(G,C,D,I) to the degree given by

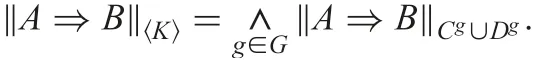
Obviously, ‖A ?B‖〈K〉is just the degree to which A ?B holds in the set IG= {Cg∪Dg|g ∈G}. We denote the fuzzy set of fuzzy decision implications by K(A ?B)=‖A ?B‖〈K〉.

Since we have formed the fuzzy set K of fuzzy decision implications in Definition 3,it is natural to apply the notations such as complete,model, and non-redundant to the case of fuzzy decision context, if the fuzzy set K is closed.

Theorem 1:The fuzzy set K is closed,i.e.K(A ?B)=‖A ?B‖K,for any A ?B.

Proof: Observing that ‖A ?B‖K=∧T∈Mod(K)‖A ?B‖Tand K(A ?B)≤‖A ?B‖Tfor each T ∈Mod(K), we have K(A ?B)≤∧T∈Mod(K)‖A ?B‖T=‖A ?B‖K.

To prove the other inequality K(A ?B)≥‖A ?B‖K, by the definitions of K(A ?B) and ‖A ?B‖K, we need to prove that

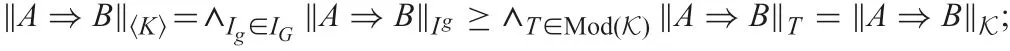
thus, it suffices to show IG?Mod(K). This is correct because, for each Ig∈IG, we have

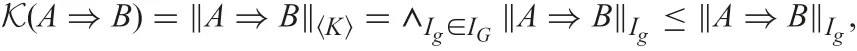
where Igis a model of Mod(K).

By Theorem 1, the fuzzy set K is closed; therefore, all the notations such as complete, model, and non-redundant, which are defined with respect to a closed fuzzy set, can now be applied to K and regarded as the notations with respect to fuzzy decision contexts. Now we say that a fuzzy set T ∈LC∪Dis a model of K,if for any A ?B we have ‖A ?B‖〈K〉≤‖A ?B‖T. We denote the set of all models of K (i.e. the fuzzy set K) by Mod(K). A fuzzy set L is complete with respect to K if it is complete with respect to K; L is non-redundant if no proper subset of L is complete.

A special set of fuzzy decision implications can be formed by using only one row of fuzzy decision context one time, i.e.I ={Cg?Dg|g ∈G}. At first glance, all of the fuzzy decision implications from I should fully hold in K, i.e. K(Cg?Dg)=1.However, it is not true in general.

Example 3: Take the object, Mercury in Table 1, as a counterexample. For h=Pluto, we have

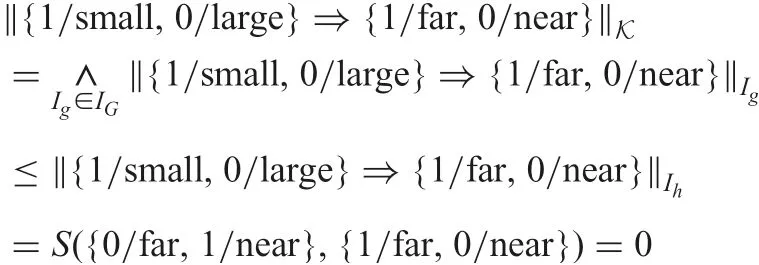
which means that the fuzzy decision implication{1/small,0/large}?{1/far,0/near} does not hold in Table 1.

In fact, for the general case, we have the following result.

Theorem 2: I ?K if and only if K is ?-consistent.

Proof: It is easily seen that I ?K if and only if K(Cg?Dg)=1 for each g ∈G. Now we have

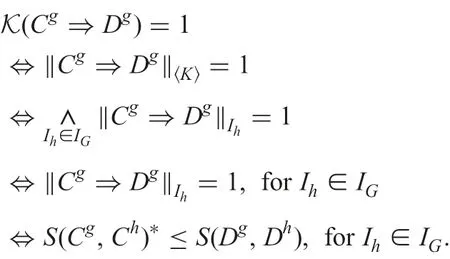
The last inequality is just the definition of?-consistent.

Theorem 2 states that for a*-consistent fuzzy decision context K,all the fuzzy decision implications in I hold in K,and that if one wants the fuzzy decision implications in I to hold in K, K has to be?-consistent.

Now we recall the notion of ‘unite closure’, which was first proposed in [13] and plays an important role in the semantical structures of decision implications [7], fuzzy decision implications[13], and variable decision implications [17].

For a fuzzy set L of fuzzy decision implications and an L-set A ∈LC, the closure of A with respect to L is an L-set defined by

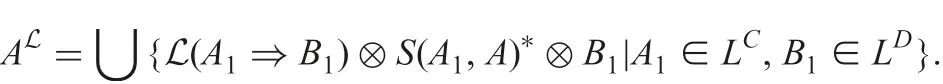
The unite closure of A with respect to L is given by A ∪AL.Closure and unite closure have the following properties [13].

Lemma 1: For any L-set A and fuzzy set L of fuzzy decision implications, we have

(i) A ∪AL∈Mod(L);

(ii) ‖A ?AL‖L=1

The first result of Lemma 1 shows that for each given L-set A ∈LC,we can obtain a model of L, which is just the unite closure of A,whereas the second says that each fuzzy decision implication with the form A ?ALcan be fully followed from L.

Concerning the fuzzy decision context, we now obtain the following result.

Theorem 3: For any A ∈LC, we have AK=ACD.

Proof: For A ∈LC, by the properties of residuated lattice, we have

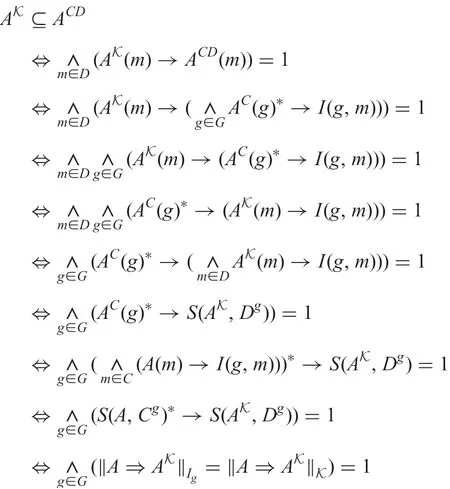
The last equation is true by Theorem 1 and (2) of Lemma 1.

On the other hand, we have AC??ACDCby the literature [16],i.e. (∧m∈C(A(m)→Cg(m)))?≤∧m∈D(ACD(m)→Dg(m)) for any g ∈G, which equals S(A,Cg)?≤S(ACD,Dg). Thus, we have ‖A ?ACD‖Cg∪Dg=1 for any g ∈G, which implies∧g∈G‖A ?ACD‖Cg∪Dg=1. We know that A ∪AKis a model of K by Lemma 1, i.e. K(A1?B1)≤‖A1?B1‖A∪AKfor any A1?B1. Particularly, K(A ?ACD)≤‖A ?ACD‖A∪AK,i.e. 1=∧g∈G‖A ?ACD‖Cg∪Dg≤‖A ?ACD‖A∪AK=S(A,A)?→S(ACD,AK)=S(ACD,AK). Thus, we have S(ACD,AK)=1 and then ACD?AK, which completes the proof.

This is the main result of the study,serving to connect fuzzy sets of fuzzy decision implications with fuzzy decision contexts, and showing that one can obtain closure and unite closure not only by means of the fuzzy set of fuzzy decision implications but also by

using the operatorsCandDin fuzzy decision context. In other words, given a fuzzy decision context K and an L-set A, one can compute ACDby the operatorsCandDin K; one can also achieve this by (i) extracting all the fuzzy decision implications from K and forming the fuzzy set K, and (ii) computing the maximal consequence AKof premise A according to K. This is correct since Theorem 3 shows that the maximal consequence AKis equal to ACD.By Theorem 3, many results from the logical study of fuzzy decision implications can be transferred to the data-driven study.For example, the following result shows how to represent models by means of the operatorsCandD.Theorem 4: Let K be a fuzzy decision context. Then we have

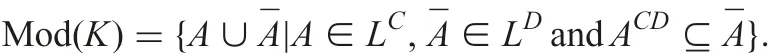
Proof: By Theorem 3, we only need to show

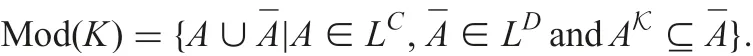
By Lemma 1, it is easy to see that Mod(K)?{A ∪AK|A ∈LC}.Furthermore, for any A1?B1we have S(B1,AK)≤S(B1, ˉA)since AK?ˉA, which yields ‖A1?B1‖A∪AK≤‖A1?B1‖A∪ˉA,i.e. A ∪ˉA ∈Mod(K).

Conversely, let T ∈Mod(K). Then, since we have K(T ∩C ?(T ∩C)L)=1 by Theorem 1 and Lemma 1, and since T is a model of K, we obtain K(T ∩C ?(T ∩C)K)≤‖T ∩C ?(T ∩C)K‖T, which yields ‖T ∩C ? (T ∩C)K‖T=1,i.e. (S(T ∩C,T ∩C)?→S((T ∩C)K,T ∩D))=S((T ∩C)K,T ∩D)=1. Thus, we obtain (T ∩C)K?T ∩D, which means

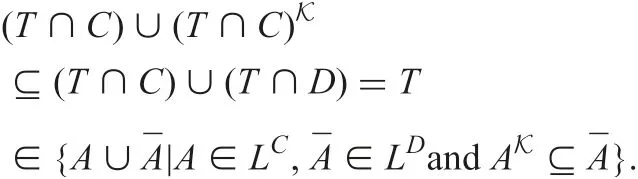
This completes the proof.

Theorem 4 shows that the set of models of K can be represented by the operatorsandThis result also implies that for any A ∈LC, ˉA=ACDis the least set to make A ∪ˉA be a model of K.

In the case of?-consistent,the unite closures of the special fuzzy sets, {Cg|g ∈G}, have simpler forms.

Theorem 5:For a?-consistent fuzzy decision context and g ∈G,we have (Cg)K=(Cg)CD=Dg.

Proof:By Theorem 3,it suffices to show(Cg)K=Dg.By definitionBy Theorem 2, we knowandthus

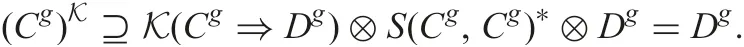
Now we have

Since the last equation is true, we have (Cg)K?Dgand thus(Cg)K=Dg. □

As another application of Theorem 3, Theorem 5 shows that in a?-consistent fuzzy decision context, the closures of the fuzzy sets{Cg}, g ∈G with respect to the fuzzy set K are just the fuzzy sets{Dg}, g ∈G.

5 From fuzzy decision implication to the fuzzy decision context

We have shown how to obtain a closed fuzzy set of fuzzy decision implications from a fuzzy decision context. In this section, we want to form a fuzzy decision context from a given fuzzy set of fuzzy decision implications and prove that the obtained fuzzy decision context has the same closed fuzzy set of fuzzy decision implications as that of the given fuzzy set. By doing this,one can study the fuzzy decision implications by studying the corresponding fuzzy decision context.

A sufficient and necessary condition for completeness based on the set of models is first adopted from[13] for later use.

Lemma 2:Let L be a closed fuzzy set of fuzzy decision implications.Then D ?L is complete if and only if Mod(D)=Mod(L).

Lemma 2 provides a convenient way to check if a subset is complete with respect to a closed set. For example, by Lemma 2, it is easy to see that for any complete fuzzy sets D1, D2, we have Mod(D1)=Mod(D2).

Lemma 3:Let L be a fuzzy set of fuzzy decision implications and setˉL(A ?B)=‖A ?B‖L. Then ˉL is a closed fuzzy set and L is complete with respect to ˉL.

Lemma 3 [13] shows that one needs only one step to get a closed fuzzy set of fuzzy decision implications, i.e. settingˉL(A ?B)= ‖A ?B‖L; moreover, the fuzzy set given is complete with respect to the closed fuzzy set obtained.

Now,for a fuzzy set L of fuzzy decision implications on C and D,we denote

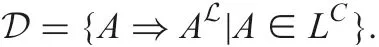
Example 4: ([14]): Let C ={x,y}, D={z} and L={0,0.5,1}.When using ?ukasiewicz adjoint pair and Identity hedge, and letting

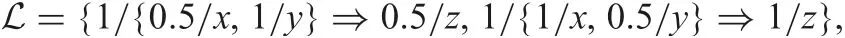
one can compute the unite closures for each A ∈LCand list the set D as follows:

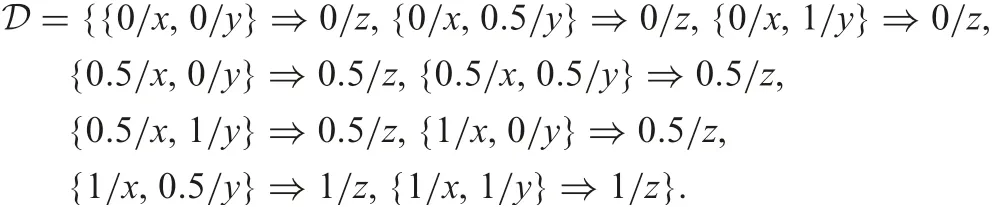
Lemma 4:D is complete with respect to Lˉ.By Lemma 4[13], D is a complete subset of ˉL; in other words,one can use the subset D in place of ˉL while keeping all the information needed.

Thus, given a fuzzy set L of fuzzy decision implications, by the complete set D, we can form a fuzzy decision context KD=(GD,C,D,ID) as follows:

· g ∈GDif and only if there exists A ?AL∈D with IC(g,m)=A(m) for m ∈C and ID(g,m)=AL(m) for m ∈D.

Theorem 6: KDis ?-consistent.

Proof: According to the definition of KD, we only need to prove that S(A1,A2)?≤S(AL1,AL2) for any A1, A2∈LC.In fact,we have

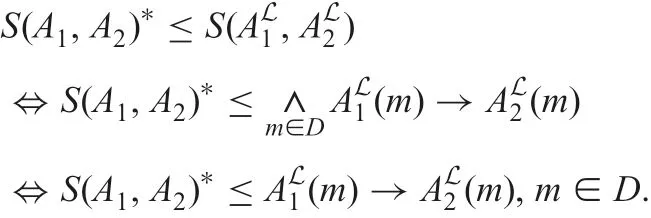
Since AL2(m)=∨A?B(L(A ?B)?S(A,A2)??B(m)) and→∨A?B(L(A ?B)?S(A,A2)??B(m))≥→(L(A1?AL1)?S(A1,A2)??AL1(m)),

we only need to prove S(A1,A2)?≤AL1(m)→(L(A1?AL1)?S(A1,A2)??AL1(m)) for any m ∈D. Thus, we need to prove S(A1,A2)?≤AL1(m)→(S(A1,A2)??AL1(m)). This is true since, by(6),we have AL1(m)→(S(A1,A2)??AL1(m))≥S(A1,A2)?.

Theroem 6 shows that the formed fuzzy decision context KDis *-consistent. Thus, by Theorem 2, all the fuzzy decision implications in I hold in K; in fact, by the construction process of KD, we have I =D. By Theorem 5, we have that for each g ∈G, (Cg)L=(Cg)CD=Dg. This is also easy to check, because for each g ∈G, by the construction process of KD, there exists A ?AL∈D such that A=Cgand AL=Dg,and by Theorem 3, we obtain (Cg)L=AL=Dg=ACD.

Just as above, we define KD(A ?B)=∧g∈GD‖A ?B‖Ig. Now,we can derive the closed fuzzy set ˉL from the obtain fuzzy decision context.

Theorem 7: We have KD= ˉL, where ˉL is given by Lemma 3.

Proof: By Theorem 3, if one can show that ACD=ALfor any A ∈LC, then it follows that AKD=AL, which yields Mod(KD)=Mod(L) by Theorem 4. Moreover, since both KDand ˉL are closed, by Lemma 2 we have KD= ˉL.

Now we show that ACD=ALfor any A ∈LC. For m ∈D, we reformulate ACD(m) as follows:

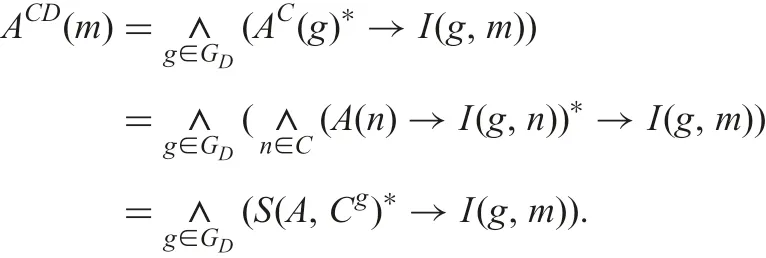
From the definition of KD, it follows that there exists h ∈GDsuch that Ch=A and Dh=AL, so we know

ACD(m)=S(A,A)?→I(h,m)∧∧{S(A,Cg)?→I(g,m)|g ∈GDand g ≠h}≤S(A,A)?→I(h,m)=I(h,m)=AL(m)

which implies ACD?AL.

To prove ACD?AL, i.e. ACD(m)≥AL(m), it suffices to show that AL(m)≤∧{S(A,Cg)?→I(g,m)|g ∈GDand g ≠h}. Now

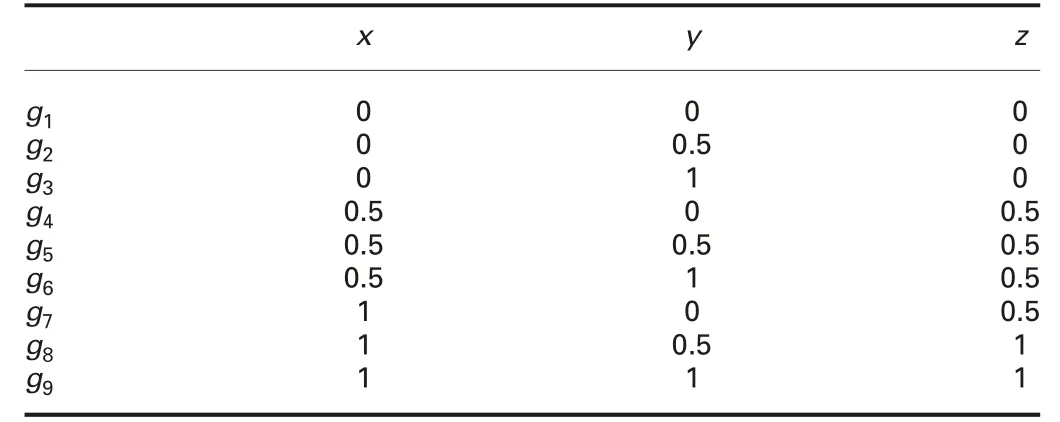
Table 2 Fuzzy decision context KD

we show that for each g ∈GD, AL(m)≤S(A,Cg)?→I(g,m). In fact, for g ∈GD, there exists B ?BL∈D such that Cg=B and Dg=BL; thus we need to show that AL(m)≤S(A,B)?→BL(m).

Then, by definition ofL, we have

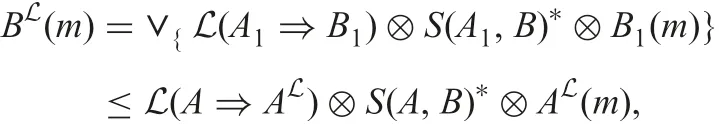
and thus

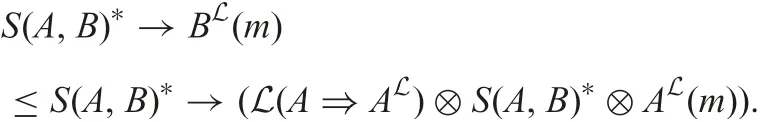
Thus, we need to prove

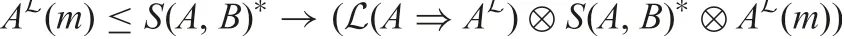
i.e. AL(m)≤S(A,B)?→(S(A,B)??AL(m)). This is true since, by(6), we have S(A,B)?→(S(A,B)??AL(m))≥AL(m). Thus we have KD= ˉL.

Example 5:(continued Example 4):By the set D,one can form the corresponding fuzzy decision context KD=(GD,C,D,ID), as shown in Table 2, each row of which is generated by one of the fuzzy decision implications in D.

Now,by Theorem 6,KDis*-consistent,where*is the identity hedge because D is computed by using ?ukasiewicz adjoint pair and identity hedge. This result can also be checked by the definition of?-consistent. For example, for the objects g3and g4, we have

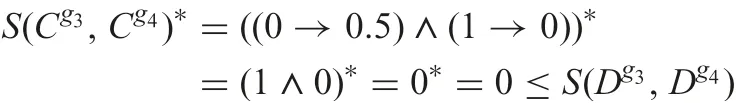
By Theorem 7, we have KD= ˉL, where L is given by Example 4 and ˉL is computed by Lemma 3. This result can be verified by checking whether KD(A ?B)= ˉL(A ?B) for any fuzzy decision implication A ?B. For example, let A ?B?{0.5/x,0.5/y}?1/z. Then, we have

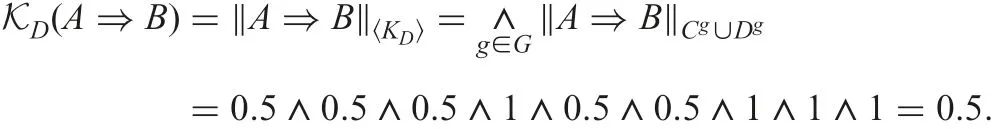
On the other hand, by Lemma 6 of [14], we have‖A ?B‖L=S(B,AL), and thus ˉL(A ?B)=‖A ?B‖L=S(B,AL)=1 →0.5=0.5.

Thus, we have KD(A ?B)=?B).

In summary,we have shown that for any given fuzzy set L of fuzzy decision implications, we can generate a complete fuzzy set D and then form a corresponding fuzzy decision context KD, and furthermore, the closed fuzzy set KDderived from KDis equivalent to the closed fuzzy set ˉL of L (Theorem 7). This implies that the fuzzy decision context obtained preserves all information from the given fuzzy set L and that one can study the fuzzy decision context instead of the given fuzzy set of fuzzy decision implications.

6 Conclusion and further work

The study intended to interpret fuzzy decision implications within fuzzy decision contexts. Thus, one can extract a fuzzy set of fuzzy decision implications from a fuzzy decision context and form a fuzzy decision context from the given fuzzy set of fuzzy decision implications. This actually establishes a correspondence between fuzzy decision contexts and fuzzy sets of fuzzy decision implications and furthermore implies the equivalence of the logic way and the data-driven way of interpreting fuzzy decision implications.

Important further works include: (i) using fuzzy concept lattice[16] to analyse the relationship between condition sub-context and decision sub-context; (ii) clarifying the effects of various hedges on the connections between fuzzy decision implications and fuzzy decision contexts; (iii) considering the data-driven way in variable decision implications [17].

7 Acknowledgments

The National Natural Science Foundation of China(no.61806116);the Natural Science Foundation of Shanxi Province (nos.201801D221175 and 201601D021076); and the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (STIP) (no. 201802014).

8 References

[1] Ganter, B., Wille, R.: ‘Formal concept analysis: mathematical foundations’(Springer, Berlin, Heidelberg, Germany,1999)

[2] Ma, J., Cai, M., Zou, C.: ‘Concept acquisition approach of object-oriented concept lattices’, Int. J. Mach. Learn. Cybern., 2017, 8, (1), pp. 123–134

[3] Wu, W., Leung, Y., Mi, J.: ‘Granular computing and knowledge reduction in formal contexts’, IEEE Trans. Knowl. Data Eng., 2009, 21, pp. 1461–1474

[4] Xu, W., Li, W.: ‘Granular computing approach to two-way learning based on formal concept analysis in fuzzy datasets’, IEEE Trans. Cybern., 2016, 46, (2),pp. 366–379

[5] Wei, L., Wan, Q.: ‘Granular transformation and irreducible element judgment theory based on pictorial diagrams’, IEEE Trans. Cybern., 2016, 46, (2),pp. 380–387

[6] Qu,K.,Zhai,Y.,Liang,J.,et al.:‘Study of decision implications based on formal concept analysis’, Int. J. Gen. Syst., 2007, 36, (2), pp. 147–156

[7] Zhai, Y., Li, D., Qu, K.: ‘Decision implications: a logical point of view’,Int. J. Mach. Learn. Cybern., 2014, 5, (4), pp. 509–516

[8] Zhai, Y., Li, D., Qu, K.: ‘Decision implication canonical basis: a logical perspective’, J. Comput. Syst. Sci., 2015, 81, (1), pp. 208–218

[9] Zhai, Y., Li, D., Qu, K.: ‘Canonical basis for decision implications’,Chin. J. Electron., 2015, 43, (1), pp. 18–23

[10] Li,D.,Zhang,S.,Zhai,Y.:‘Method for generating decision implication canonical basis based on true premises’, Int. J. Mach. Learn. Cybern., 2017, 8, (1),pp. 57–67

[11] Qu, K., Zhai, Y.: ‘Generating complete set of implications for formal contexts’,Knowl.-Based Syst., 2008, 21, pp. 429–433

[12] Li, J., Mei, C., Kumar, C.A., et al.: ‘On rule acquisition in decision formal contexts’, Int. J. Mach. Learn. Cybern., 2013, 4, (6), pp. 721–731

[13] Zhai,Y.,Li,D.,Qu,K.:‘Fuzzy decision implications’,Knowl.-Based Syst.,2013,37, pp. 230–236

[14] Zhai, Y., Li, D., Qu, K.: ‘Fuzzy decision implication canonical basis’,Int. J. Mach. Learn. Cybern., 2018, 9, pp. 1909–1917

[15] Zhai, Y., Li, D., Qu, K.: ‘Reverse study of formal concept analysis’, J. Front.Comput. Sci. Technol., 2014, 8, (12), pp. 1511–1516

[16] Bělohlávek, R.: ‘Fuzzy relational systems: foundations and principles’ (Kluwer Academic Publishers, Norwell, MA, USA, 2002)

[17] Zhai,Y.,Li,D.,Zhang,J.:‘Variable decision knowledge representation:a logical description’, J. Comput. Sci., 2018, 25, pp. 161–169