D.G. Prksh , P. Veeresh

a Department of Mathematics, Faculty of Science, Davangere University, Shivagangothri, Davangere-577007, Karnataka, India

b Department of Mathematics, Karnatak University, Dharwad-580003, Karnataka, India

Abstract The pivotal aim of the present investigation is to find an approximate analytical solution for the system of three fractional differential equations describing the Lakes pollution using q - homotopy analysis transform method ( q -HATM).We consider three different cases of the considered model namely, periodic input model, exponentially decaying input model, and linear input model.The considered scheme is unifications of q -homotopy analysis technique with Laplace transform (LT).To illustrate the existence and uniqueness for the projected model, we consider the fixed point hypothesis.More preciously, we scrutinized the behaviour of the obtained solution for the considered model with fractional-order, in order to elucidate the effectiveness of the proposed algorithm.Further, for the different fractional-order and parameters offered by the considered method, the physical natures have been apprehended.The obtained consequences evidence that the proposed method is very effective and highly methodical to study and examine the nature and its corresponding consequences of the system of fractional order differential equations describing the real word problems.

Keywords: Lakes system; Atangana-Baleanu derivative; Laplace transform; Fixed point theorem; q -Homotopy analysis method.

1.Introduction

The essence of mathematical tools for exemplifying the practical problems exist in daily life is as antic as the creation of the world.The growth of science and technology were recently accomplished grate attentions of the researcher with the aid of mathematical models in order to understand, describe, and predict future the behaviour of the natural phenomena.A mathematical model is a portrayal of a system by means of mathematical rules, formulas, theories and methods.Humankind has invented the most influential mathematical concepts known as calculus with the integral and differential operators, which can consider to model and simulate numerous mechanisms arising in the environment where he lives in the past decades.The concept of calculus is introduced and natured by grate mathematicians Newton and Leibniz in order to illustrate the physical models based on the rate of change.Later, it considered as a highly me- thodical and very efficient weapon to deal with all complex problems and also understand their corresponding conse- quences which play a vital rule in the betterment of the living beings.

Recently, many researchers pointed out and also illustrated that the integer-order differential operators are not always appropriate tools to model the complex and nonlinear phe- nomena.This is due to the fact that classical derivatives fail to capture essential physical properties like anomalous diffu- sion, non-Markovian processes, random walk, long-range, and most importantly heterogeneous behaviours.The concept of local differential operators along with the power-law setting and non-local differential operators was suggested in order to accurately replicate above-cited natural processes.The com- plexities of nature have led mathematicians and physicists to derive the most sophisticated and scientific mathematical op- erators to accurately replicate and capture pragmatic realities.Soon after the birth of classical calculus, the fractional cal- culus is derived as a consequence of correspondence between Leibniz and L’Hopital.Even though it is almost 324 years in 2019, recently it magnetizes the great consideration of many researchers from all accompanying areas of science [1–6] .

Due to the fast growth in the computer software and math- ematical algorithms, from the last twenty years, humankind is magnetised towards the innovations and research in the area of fractional calculus [7–32] .There is diverse definitions are derived and presented by many pioneers.However, each interpretation has its own drawback.The Riemann–Liouville derivative is inept while describing the significance of the initial condition and fails to satisfy the classical case of the derivative of the constant is zero.Later Caputo derived a new derivative which satisfies the classical case and it also ex- plains the significance of the initial condition but fails to il- lustrate the singular kernel of the model.Caputo and Fab- rizio in 2015 suggested a new definition which overcomes all the above-cited obliges [33] , and later this definition has been applied to many complex non-linear problems in or- der to capture their interesting behaviours.Recently, many mathematicians and physicist criticized about this differential operator due to its confines to explained very essential proper- ties like, the kernel applied was non-local and the associated anti-derivative is just the average of the function and its in- tegral.In order to overcome all these limitations, Atangana and Baleanu in 2016 suggested a new fractional differential operator.This derivative is natured with the aid of generalised Mittag–Leffler function [34] ; this function has been familiar- ized to provide a response to the conventional question of complex analysis, specifically to describe the process of the analytical continuation of power-law series outside the sick of their conference.The consequence of the Mittag-Leffler func- tion was exposed while its affiliation to calculus with frac- tional order is very essential.Hence, the considered deriva- tive is able to incorporate the essential properties in order to understand nature better and systematic manner.Particu- larly, the phenomena are highly dependent on its history and time.Since then, this derivative is considered to examine and understand the diverse class of natural phenomena.

Around the globe, contamination effects quality in the Lakes water.The pollution is mainly due to industrial, agri- cultural and municipal sources; for instance, sewage, herbi- cides, pesticides, and litter.As compared to the surrounding environment and landscapes, lakes often contain huge pol- lution levels.Some aquatic-organisms species are predomi- nantly delicate to pollution; they are considered as pointers of pollution.While chemicals are spilt, they can groove into nearby streams and be ecstatic downstream into lakes.

In order to demonstrate the efficiency of the proposed al- gorithm and novel derivative, in this paper we consider the system of three equations describe the Lakes pollution.The model is portraying the pollution of a system of three lakes [35] as presented in Fig.1 .The amount of water in all the three lakes assumed to be fixed, and also the pollutant in each lake is distributed uniformly.Further, each lake is taken as the huge compartment and the pipes are considered in or- der to interconnect between the compartments [36] .Here, we analysed three different cases namely, periodic, linear, and exponentially decaying.For example, the pollution is intro- duced into Lake 1 from a factory at the rateP(t)and then the polluted water flows through the pipes or channels into the remaining lakes as presented by the arrows.By consider- ing above-cited assumptions, we try to analyse the pollution level in each lake att≥0.

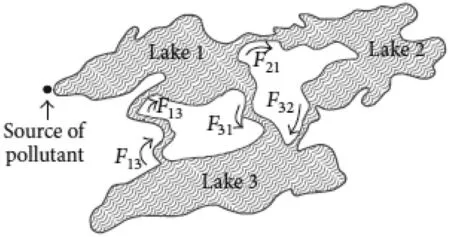
Fig.1.System of three lakes interconnecting with channels.

Now, at the timet≥0 the concentration of the pollutantci(t) in Lakeiwith the volume of waterViand the amount of pollutantxi(t) is given by the relation

The flow rateFijfrom Lakeitojis assumed as constant, then fort≥0 the fluxrjipollutant flowing from Lakeitojis presented as

For timet, the above relation gives the rate at which the pollutant concentration in Lakeiflows intoj.By using below principle to each Lakes

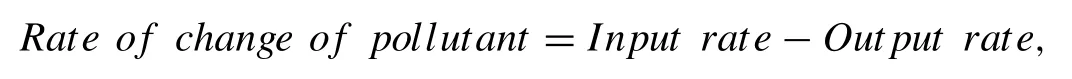
we obtained the system of three equations

wherex1(t),x2(t) andx3(t) are respectively denotes the amount of pollutant in Lakes 1, 2 and 3,F13is flow rate from Lake 1 to Lake 3 and similarly others.Here, it clear that the in- coming and outgoing flow rate in each Lakes is constant and hence water volume in each lake is fixed and also it leads the following conditions

In order to analyse the behaviour of the defined model, we consider the particular values of the parameters cited in the above system form [37] and which are as follows

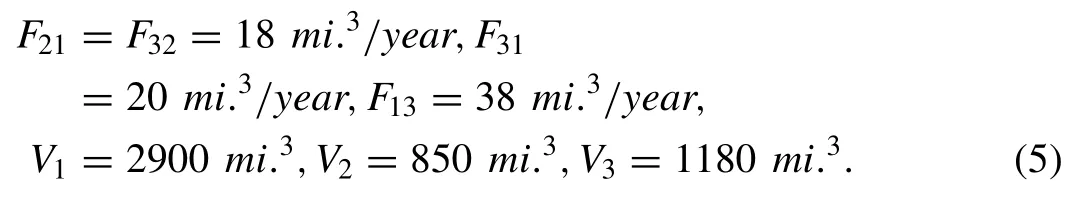
In the present study, we consider the system ( 3 ) with frac- tional order as follows

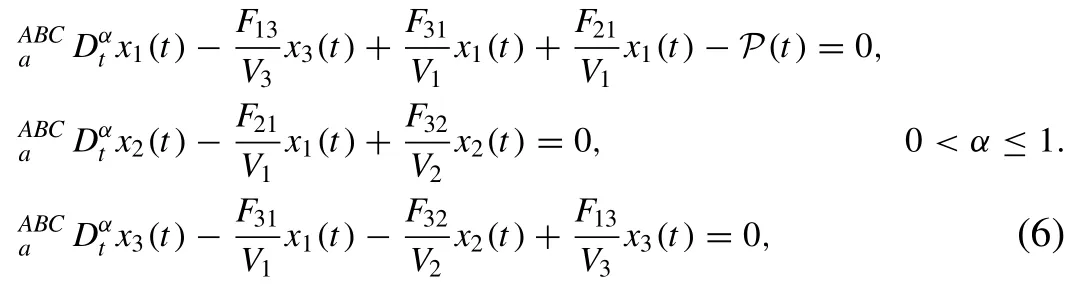
whereαis fractional order.

In order to find the solution for differential and integral equations describing the diverse class of phenomena exist in nature and analyse the corresponding consequences, recently many pioneers established sophisticated and very efficient al- gorithms.There have been many methods in the literature to solve nonlinear differential equations.The efficient and more accurate method in this epoch is the homotopy anal- ysis method (HAM) [38–39] .From 1992 onwards it has been employed the diverse class of nonlinear problems describing various phenomena exists in daily life.However, this method has to need huge computer memory and time.There is a necessity of combination of this technique with acquainted transformation methods in order to overcome obliges men- tioned above.

In this paper, we considerq-HATM to find the solution and also capture the corresponding consequences of the pro- posed model.The proposed scheme is a mixture ofq-HAM with LT [40] .The novelty is its methodical and systematic algorithm and it proposed by two parameters namely, axillary and homotopy parameters ( ? andn).These parameters help us to control and adjust the convergence region and provide swift convergence.Since HAM does not require perturbation, linearization, or discretization while solving the complex non- linear differential equations and the proposed method is an en- hanced method of HAM and hence it does not requires them.Theq-HATM can decrease the computational work and huge time as related to other classical techniques while preserving great accuracy.The future technique has many sturdy proper- ties including straight forward solution procedure, promising large convergence region, and moreover free from any as- sumption, discretization and perturbation.From the last three years, due to efficiency and applicability of the proposed algo- rithm, it has been extensively employed for various nonlinear problems by many authors to analyse and capture the physi- cal behaviours and their corresponding consequences [41–48] .For instance, authors in [49] capture the behaviour of imag- inary part of theq-HATM solution in terms contour plots for the fractional generalized Zakharov equations, authors in [50] presented the efficiency of considered method while studying the system of equation describing the three-species food chain model arising in the realm of mathematical ecol- ogy, the nature of obtained solution with respect to homotopy parameters for the equation describing the water transport in unsaturated porous media is presented in [51] , and many au- thors have been proved that the considered method is highly effective to examine wild class of mathematical models arisen in science and technology.

The considered model recently influenced the attention of many scholars.For instance authors in [37] hired variational iteration scheme in order to solve and analyse the pollution of lake system, the homotopy perturbation technique is ap- plied by authors [52] to find the solution for cited model, and also presented some interesting results, authors in [53] consid- ered He’s variational iteration algorithm in order to present the effectiveness of the method while solving the pollution model, researchers in [54] are employed modified differential transformation technique, many authors considered different schemes in order to analyse the considered model [35–36 , 55] .

In the present era, the study of ocean engineering magne- tizes the attention of many researchers.The study of marine environmental engineering, aquacultural engineering, coastal engineering, oceanophysics, marine chemistry, pipeline and riser technology, and many others are very important subdi- vision of the ocean engineering.By the help of these stud- ies, mankind can design and construct dams, levees, canals, Lakes and complex tide abatement systems.In this connec- tion, mathematics plays a vital role in order to reduce time, cost, human power and others by making computational mod- els to study complicated problems into simple way.Many equations describe the related model of ocean engineering, which are examined with the help of mathematical methods [64–66] .In the present framework, we consider the system of three fractional differential equations describing the Lakes pollution and presented the corresponding consequences in the form of mathematical model in order to understand and capture behaviour of the real word problems with simple and efficient technique.Moreover, we ensure that the considered model is highly dependences on time instant and its history, these futures can be incorporate and methodically described by the help of newly defined fractional operator.Further, we illustrated the existence and uniqueness for the projected model with respect to the newly defined fractional deriva- tive using fixed point hypothesis.The present investigation can help to young researchers to study and solve many real world problems arises in various phenomena associated to ocean engineering and science.

2.Preliminaries

The basic notions of the novel fractional derivative and Laplace transform are presented in this segment [56–58] .

Definition 1.Letf∈H1(a,b)(b>a,α∈ [0, 1]) be a function, and then its fractional Atangana-Baleanu-Caputo derivative is defined as

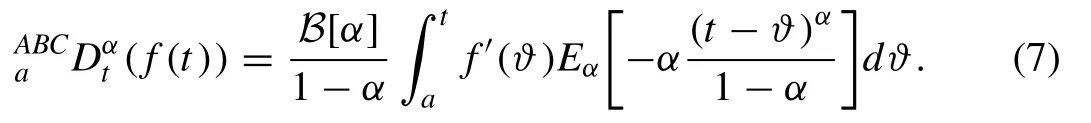
Definition 2.Letf∈H1(a,b),b>a,α∈ [0, 1] be a function, and then its fractional-order Atangana-Baleanu in Riemann- Liouville (RL) sense is given by

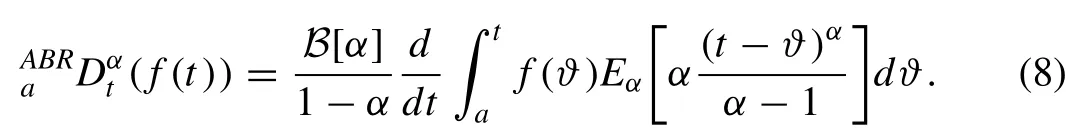
Definition 3.With respect to the non-local kernel, the frac- tional AB integral is presented as follows

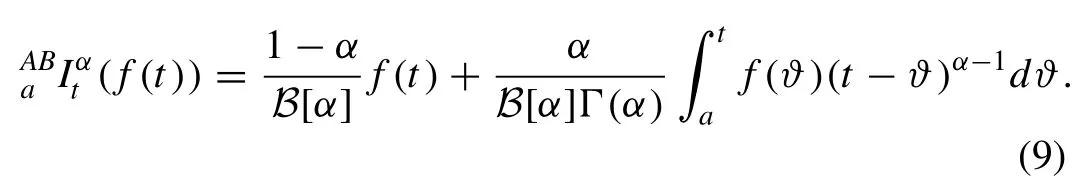
Definition 4.Laplace transform (LT) off(t) with respect to fractional AB derivative is

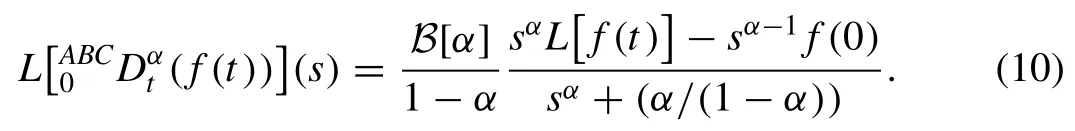
Theorem 1.FortheRLandABderivatives,thebelowdefinedLipschitzconditionsrespectivelyholdtrue[16]

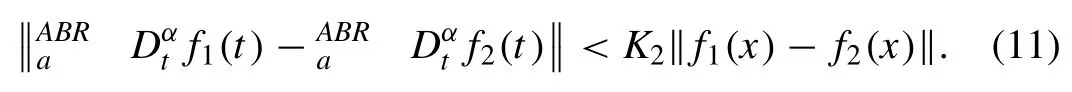
and

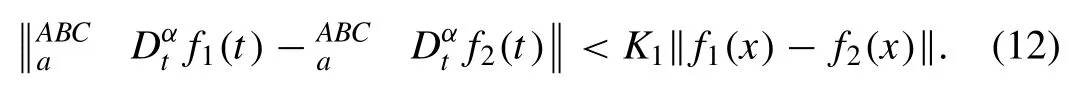
Theorem 2.Thedifferentialequationwithfractionalorderhasauniquesolutionandwhichisdefinedas[16]

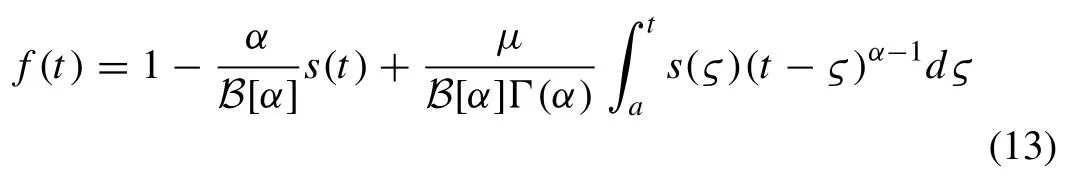
3.Fundamental solution procedure of q -HATM

In this segment, to illustrate the solution procedure of the proposed technique we consider fractional differential equa- tion [59–60]

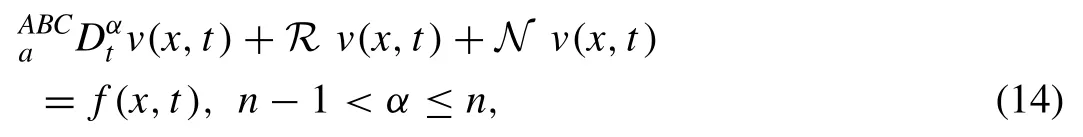
with the initial condition

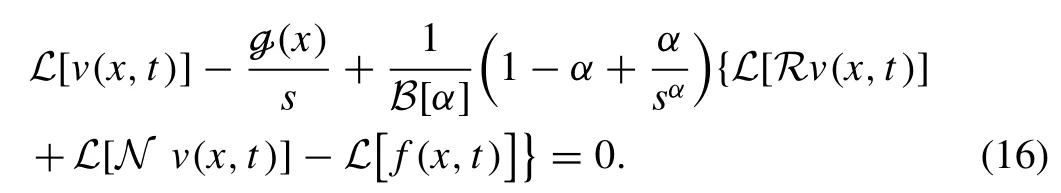
Then we define the nonlinear operator for corresponding real-valued function?(x,t;q)

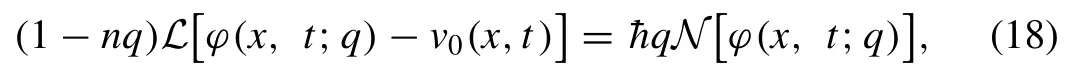
whereLis signifyingLT,is the embedding parameter andis an auxiliary parameter.Forq= 0 and, the results are given below hold true

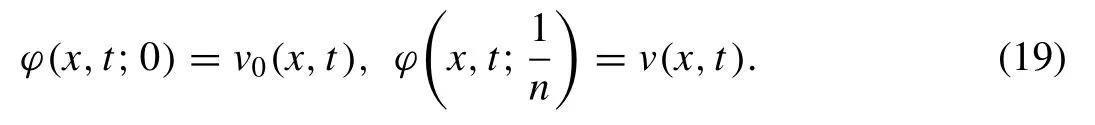
Now, by intensifyingqfrom 0 tothen?(x,t;q) varies fromv0(x,t) tov(x,t).By applying Taylor theorem near toq, we have

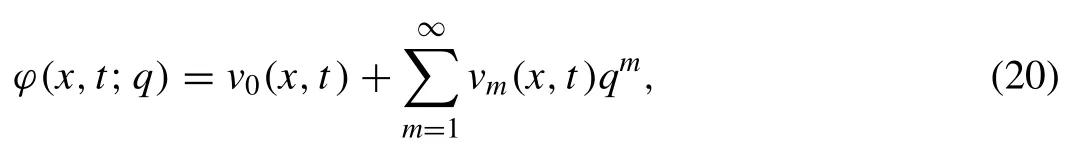
where

For the proper chaise ofv0(x,t), the series ( 17 ) converges atnand.Then

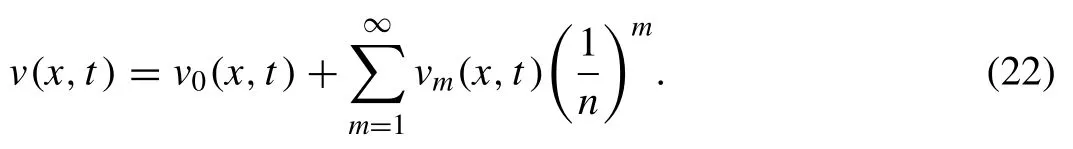
Onm-times differentiating Eq.(18) withqand then multiply

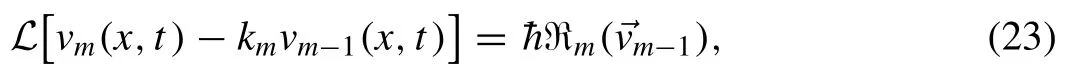
where the vectors are defined as

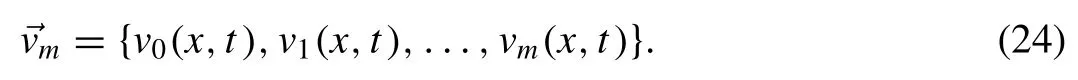
On applying inverseLTto Eq.(23) , it reduces to

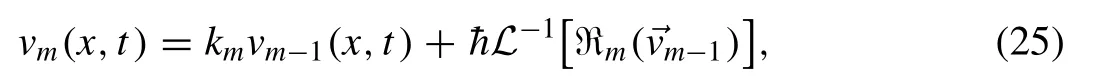
where

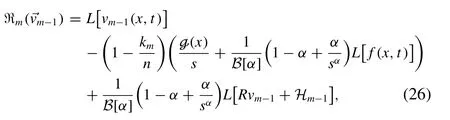
and

In Eq.(26) ,Hmis homotopy polynomial and which is defined as

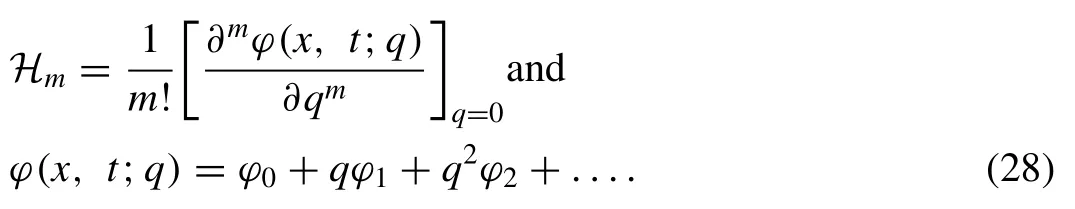
By the aid of Eqs.(25) and (26) , one can get

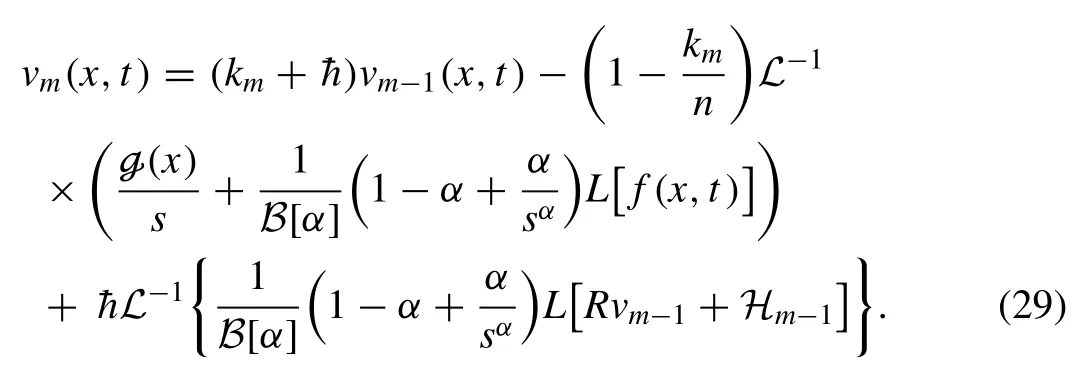
Then, the terms ofvm(x,t) can be getting by the help of Eq.(29) .Theq-HATM series solution is defined below

4.Solution for proposed model

Here, we consider the model defined in Eq.(6) to find the solution by using the proposed method

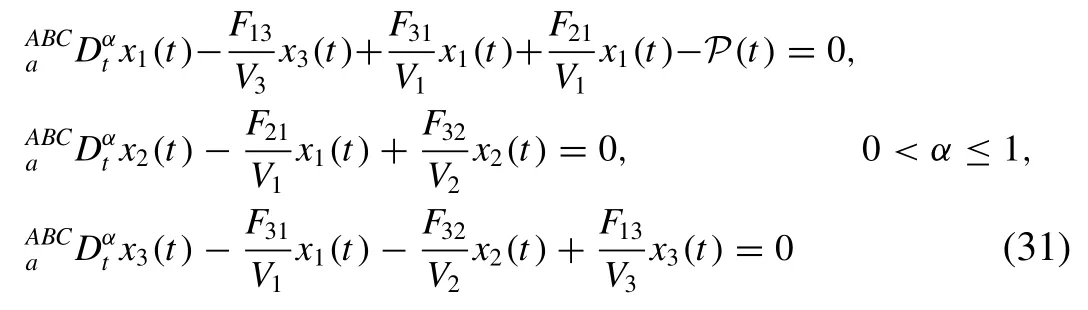
with initial conditions

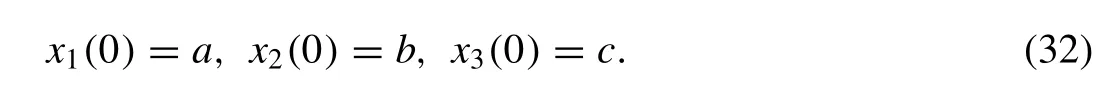
TakingLTon Eq.(31) and then using the Eq.(32) , we get

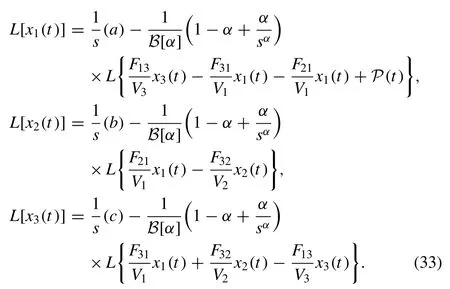
Now, we present the non-linear operatorNas

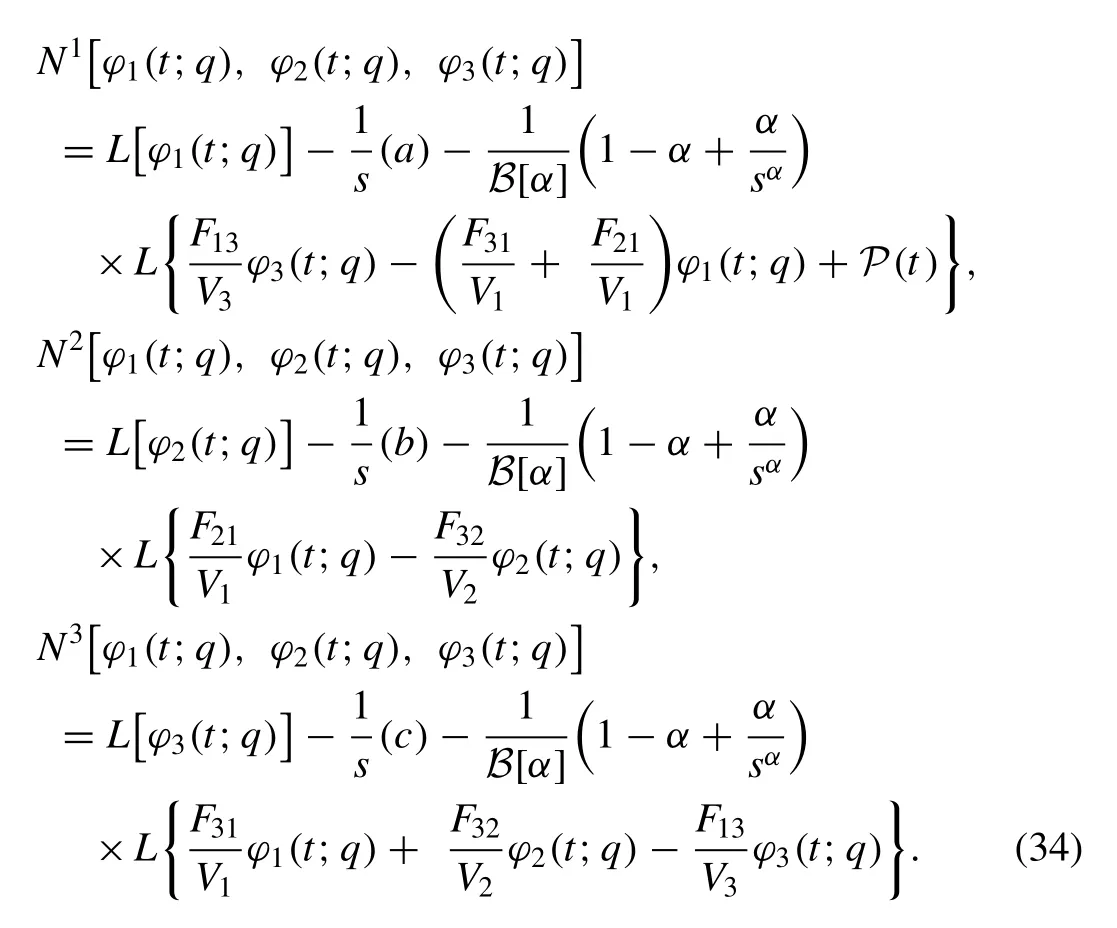
The deformation equation ofm-thorder using theq-HATM atH(x,t)= 1 , is given as follows

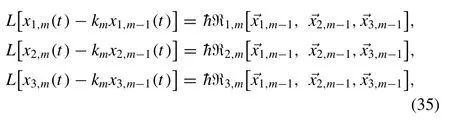
where

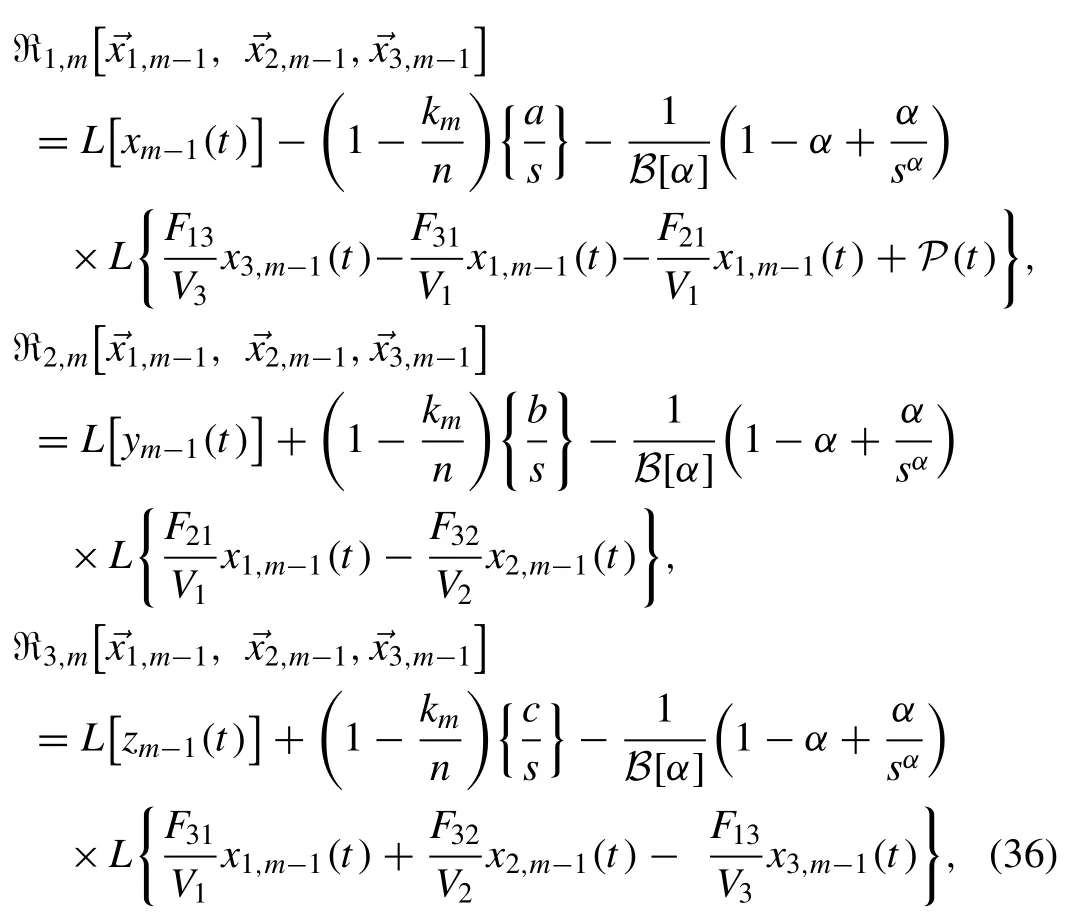
By employing inverseLTon Eq.(35) , we get

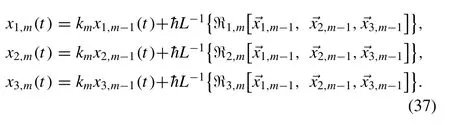
On solving the above systems by the help of initial conditions, we can obtain the components of the

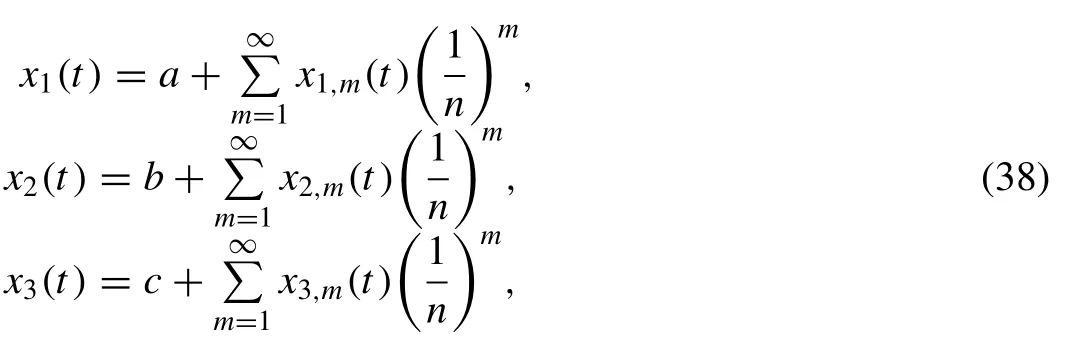
5.Existence of solutions for the considered fractional system

For the solution of the considered system, in this segment, we present the existence and uniqueness with the help of fixed-point hypothesis.Now, the system ( 31 ) is considered as follows:

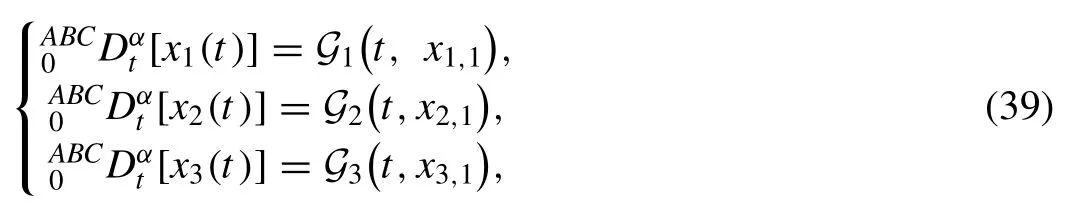
By the help of Theorem 2 and Eq.(39) we have

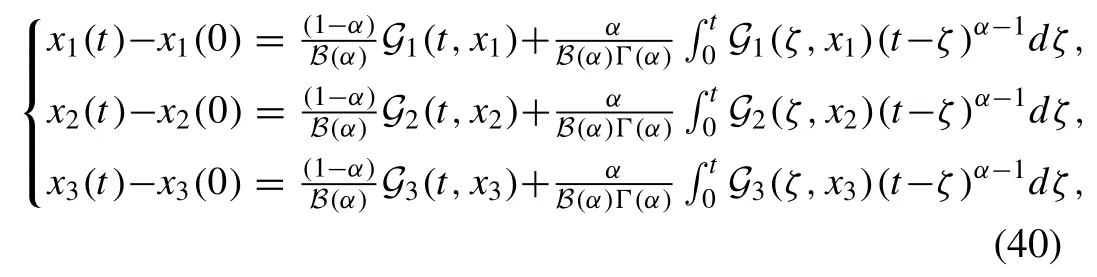
Theorem 3.ThekernelG1gratifiestheLipschitzconditionandcontractionifsatisfies1 .

Proof.We choose the two functionsx1andx1,1in order to evidence the above-cited theorem, then

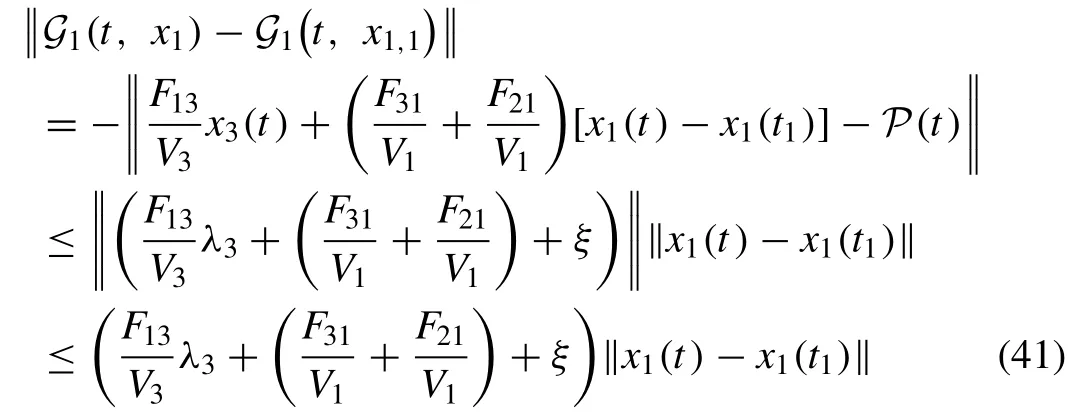
where ‖x3(t) ‖ ≤λ3is a bounded function and also ‖P(t)‖ ≤ξ.Puttingη1=+ξin Eq.(41) , one can get

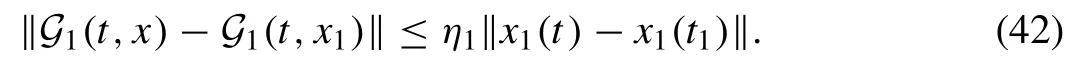
The above condition shows that the Lipschitz condition is obtained forG1.Further, if 0 ≤1 , then it leads to contraction.We can similarly verify the remaining cases, and which are presented as

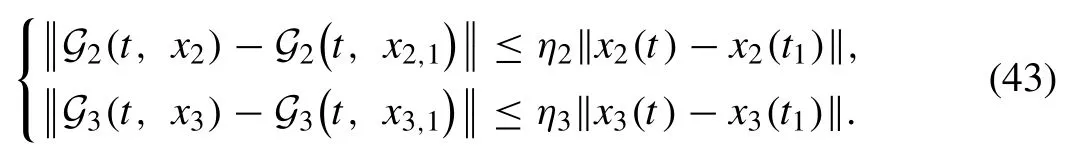
Now, we present the recursive form of the foregoing as

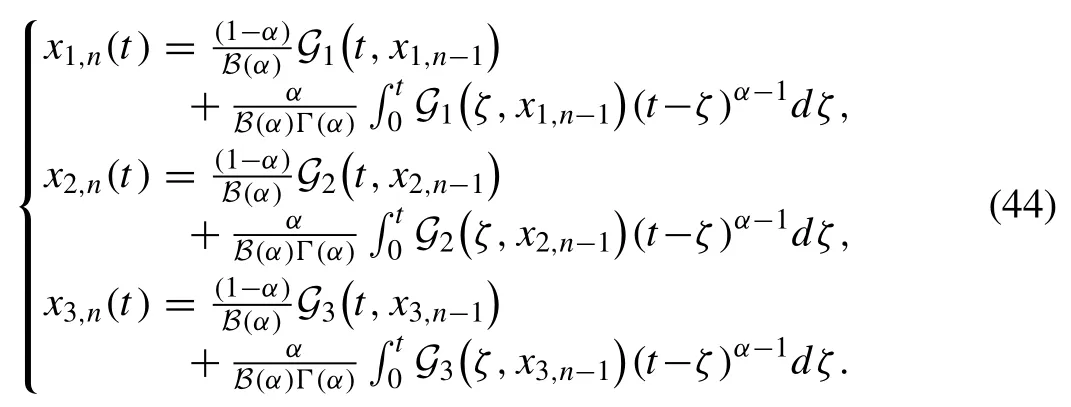
The associated initial conditions are

Then between the terms, we present the successive difference as follows

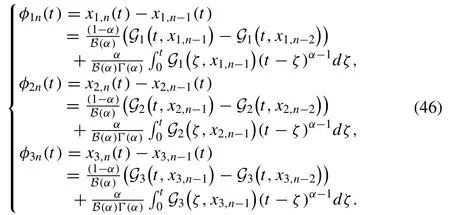
Notice that

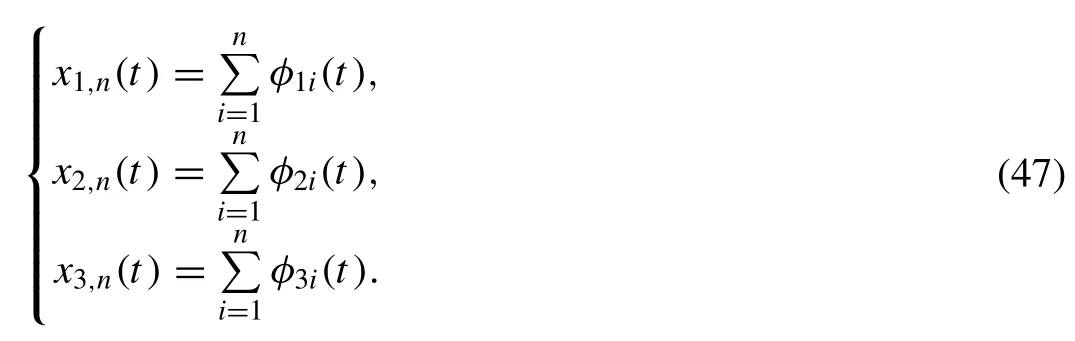
By plugging norm on the first term of Eq.(46) , and then by the assist of Eq.(43) , we have

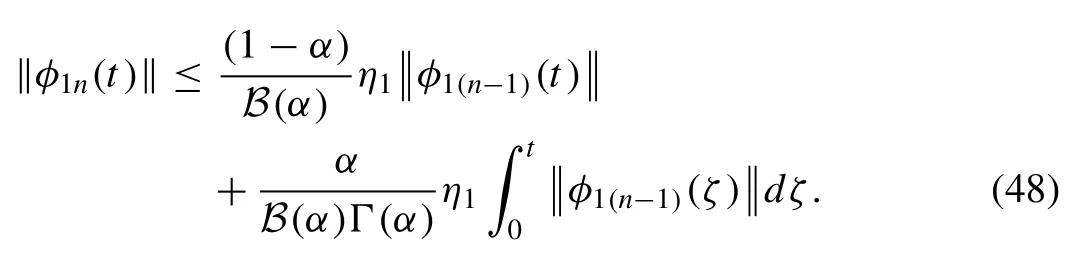
Similarly, we get

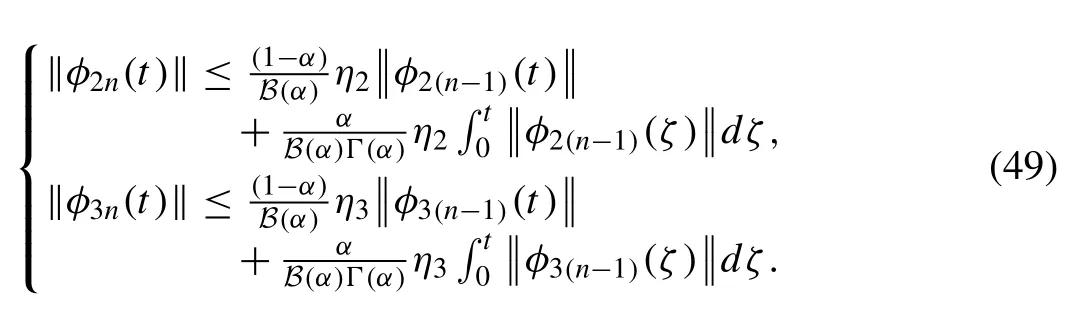
By the help of the preceding result, we verify the following theorem

Theorem 4..Thesolutionfortheproposedsystem(31)willexistanduniqueiffortheparticulart0wehave

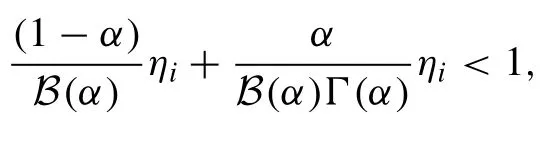
fori= 1,2 and 3.

Proof.Letx1(t),x2(t) andx3(t) be the bounded functions grat- ifying the Lipschitz condition.By the help of Eq.(47) and Eq.(49) , we obtain

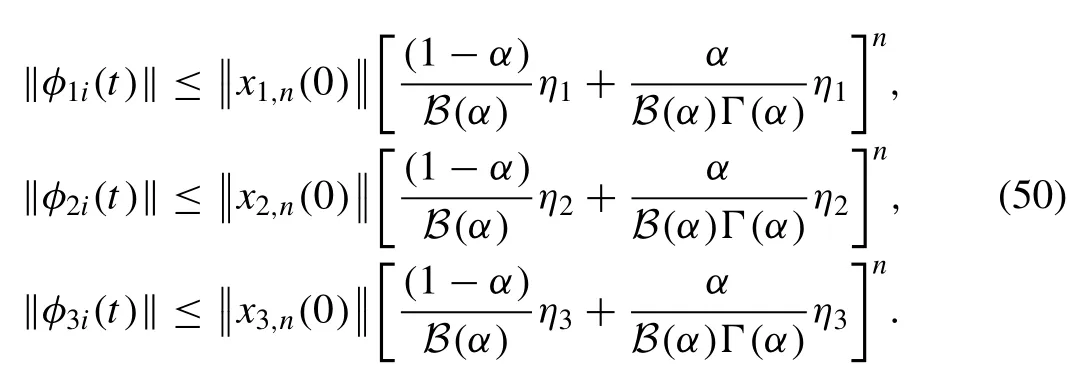
For the obtained solutions, this proves the continuity and existence.Then, we consider in order proving the above system is a solution for the considered model defined in Eq.(31)

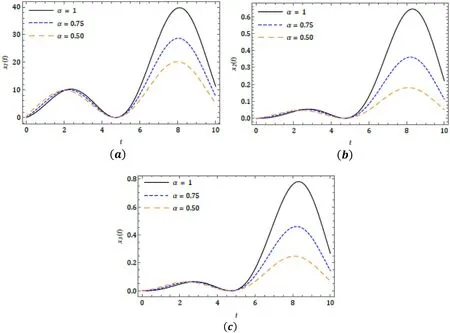
Fig.2.Behaviour of q -HATM solution for ( a ) x 1 ( t ), ( b ) x 2 ( t ) and ( c ) x 3 ( t ) at ˉh = ?1 and n = 1 for the Case 1.

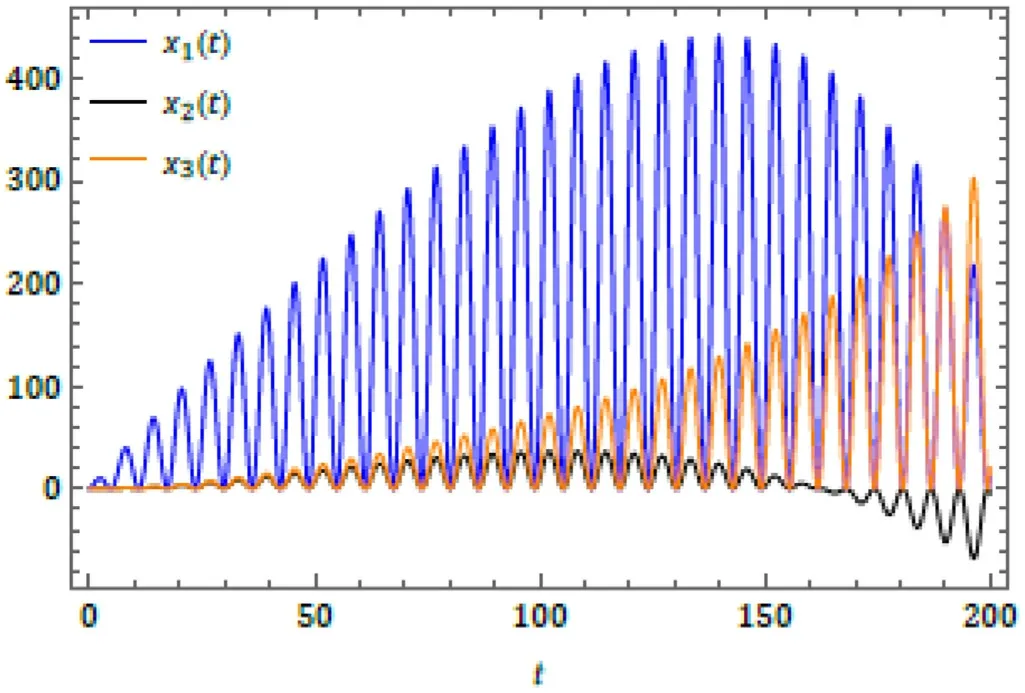
Fig.3.Response of time series for the Case 1 at ˉh = ?1 , α = 1 and n = 1 .

Now, we consider the below condition in order to prove the required results

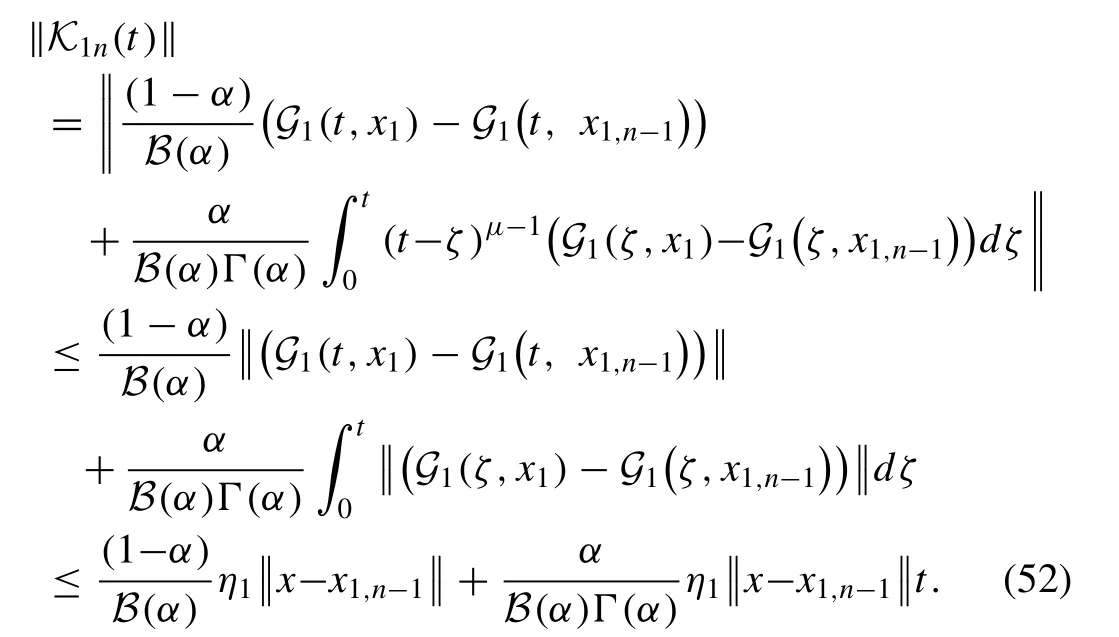
Similarly, att0we can obtain

We can see that form Eq.(53) , asntends to ∞ , then ‖K1n(t)‖ approaches to 0.In the same manner, we can prove for‖K2n(t)‖ and ‖K3n(t)‖ .

Next, prove the uniqueness for the solution.Assume that,be the set of different solution with respect tox1(t),x2(t) andx3(t), then we get

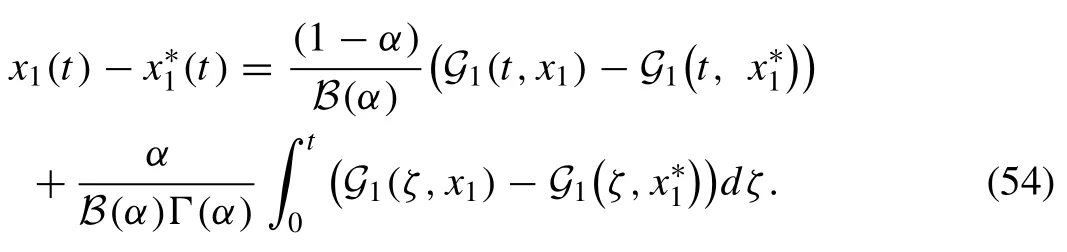
Eq.(54) simplifies on applying norm, and then we have

On simplification

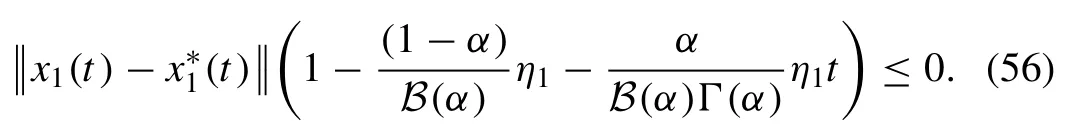
From the above condition, it is clear thatx1(t)=(t), if

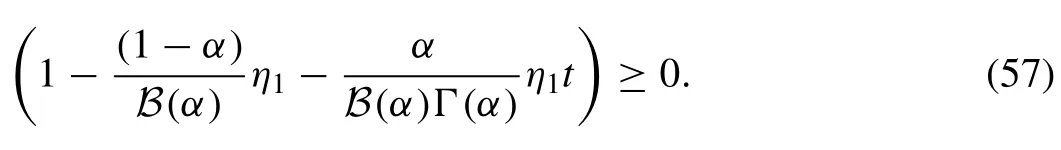
Therefore, Eq.(57) proves the theorem.

6.Numerical results and discussion

In this segment, to present the effectiveness of the proposed method we consider three different cases, and also find the solution for the corresponding cases.

Case 1: Periodic Input Model

In this case, the model considered while pollutant is peri- odically applied into Lake 1.As a particular case, we choseP(t)=asin(ωt)+c, whereαandωare respectively the variations amplitude and frequency andcis the average input of pollutant concentration.Then, we have from Eq.(31) witha=ω=c= 1

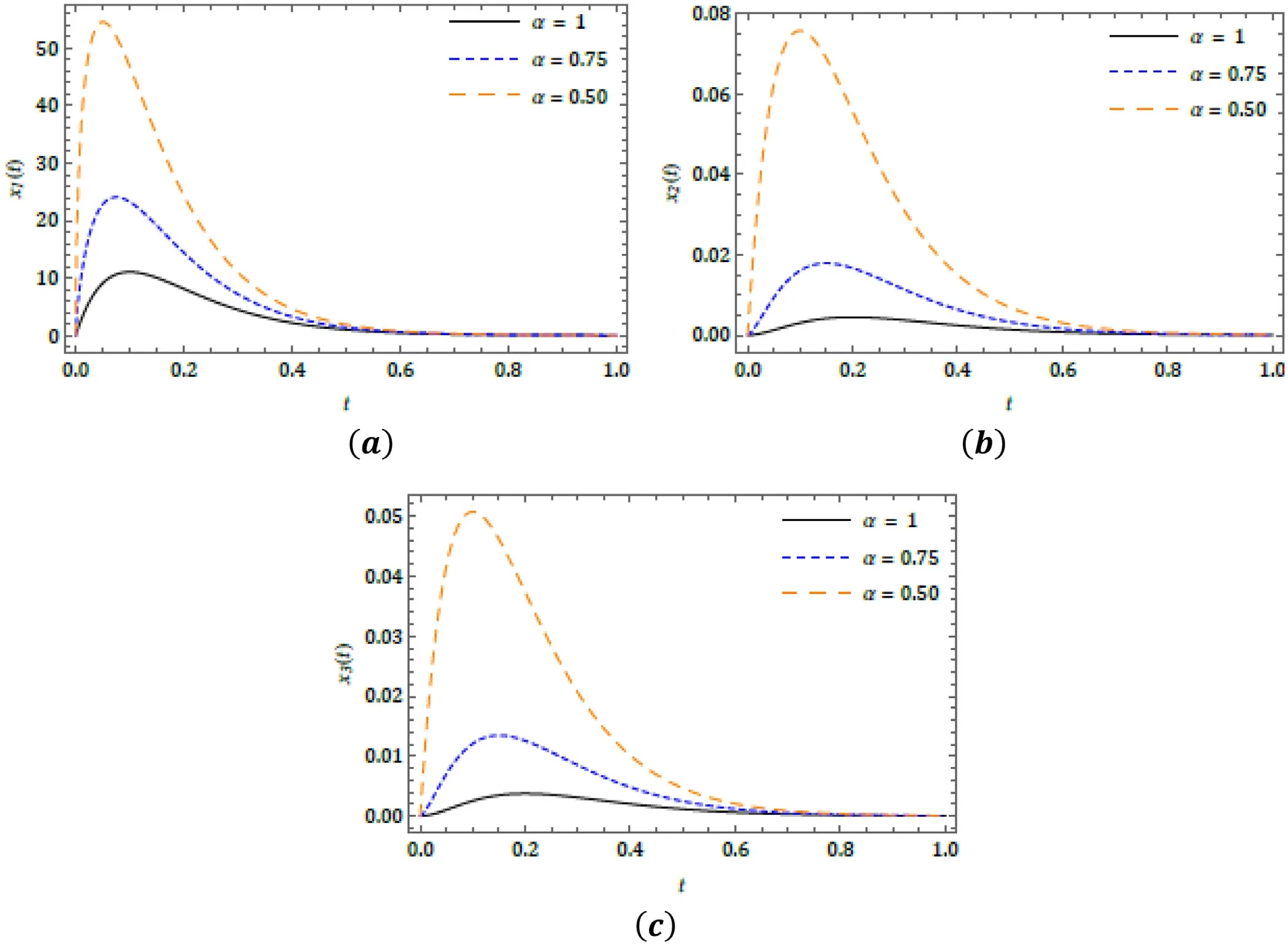
Fig.5.Behaviour of q -HATM solution for ( a ) x 1 ( t ), ( b ) x 2 ( t ) and ( c ) x 3 ( t ) at ˉh = ?1 and n = 1 for the Case 2.

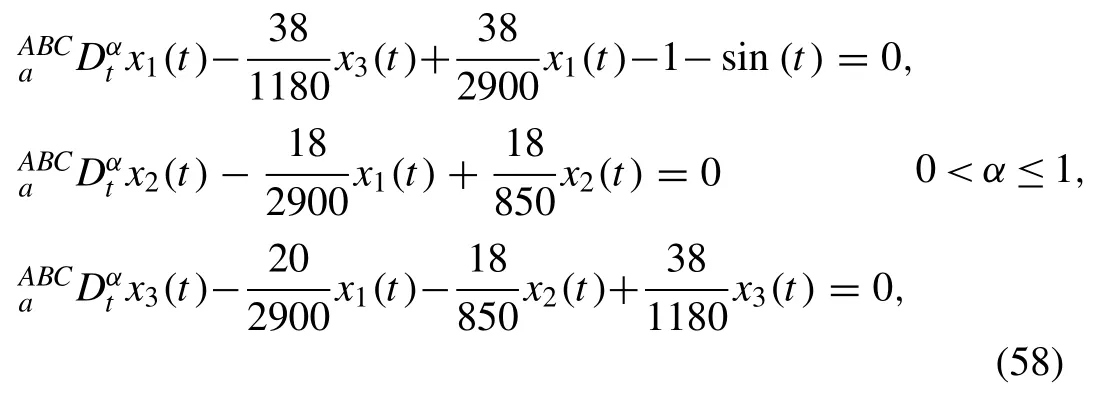
with initial conditions

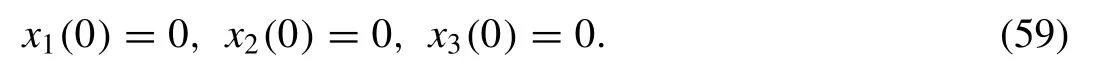
Then, by the help of the above conditions, Eq.(36) and Eq.(58) , the Eq.(37) gives withx1,0= 0,x2,0(0)= 0 andx3,0(0)= 0 as follows

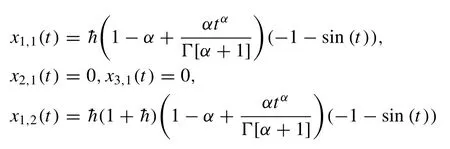
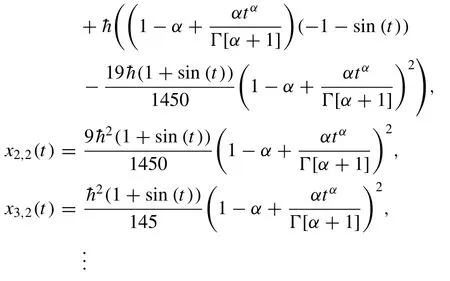
Case 2: Exponentially Decaying Input Model

In this case, the model considered when pollutant with massive dumping.As a particular case, we choseP(t)=ae?bt.Then, we have from Eq.(31) witha= 200 andb= 10

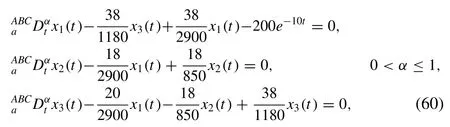
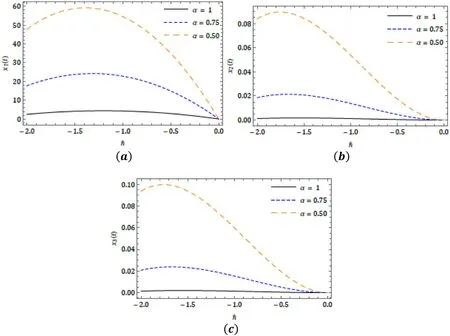
Fig.6.? -curves for ( a ) x 1 ( t ), ( b ) x 2 ( t ) and ( c ) x 3 ( t ) with distinct α at n = 1 and t = 0. 01 for the Case 2.

with initial conditions

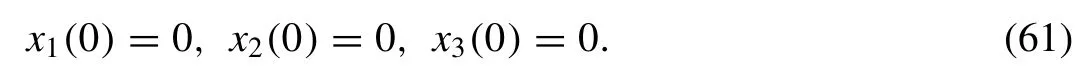
Then, by the help of the above conditions, Eq.(36) and Eq.(60) , the Eq.(37) gives withx1,0= 0,x2,0(0)= 0 andx3,0(0)= 0 as follows

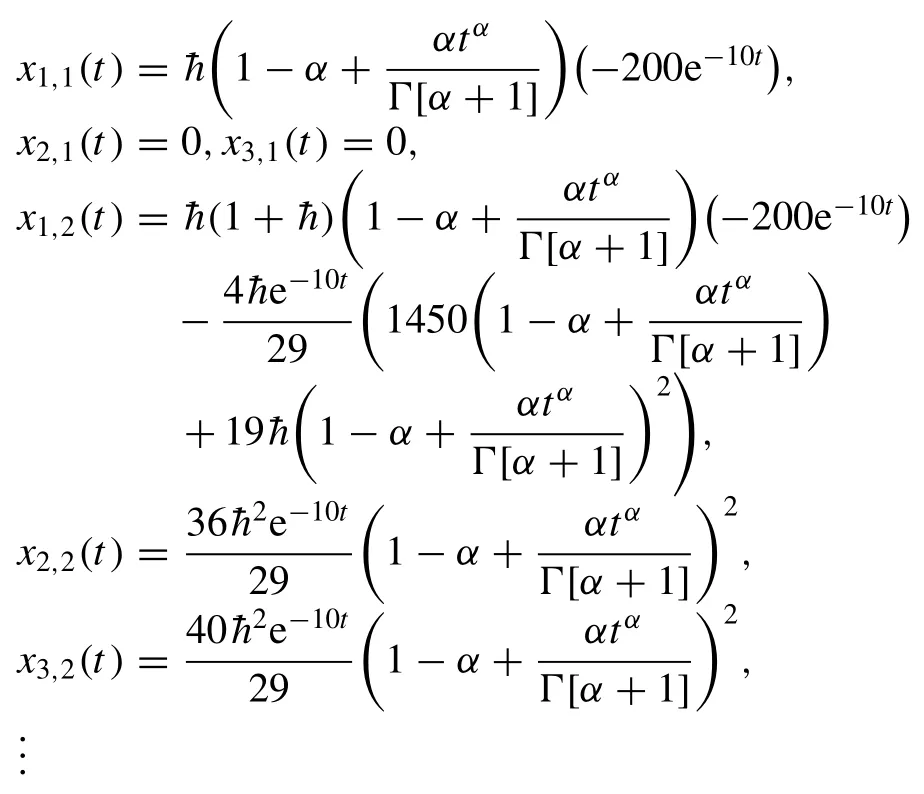
Case 3: Linear Input Model

In this case, the model considered while Lake 1 has a pollutant with a linear concentration.As a particular case, we choseP(t)=at.Then, we have from Eq.(31) witha= 100

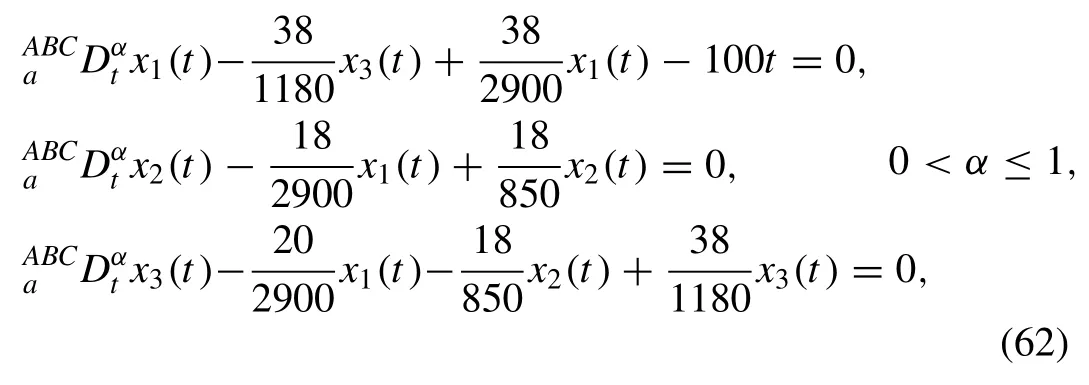
with initial conditions

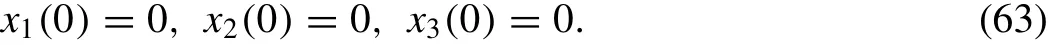
By the help of the above initial conditions, Eq.(36) and (62) , then the Eq.(37) gives withx1,0= 0,x2,0(0)= 0 andx3,0(0)= 0 as follows

Fig.7.Behaviour of q -HATM solution for ( a ) x 1 ( t ), ( b ) x 2 ( t ) and ( c ) x 3 ( t ) at ˉh = ?1 and n = 1 for the Case 3.

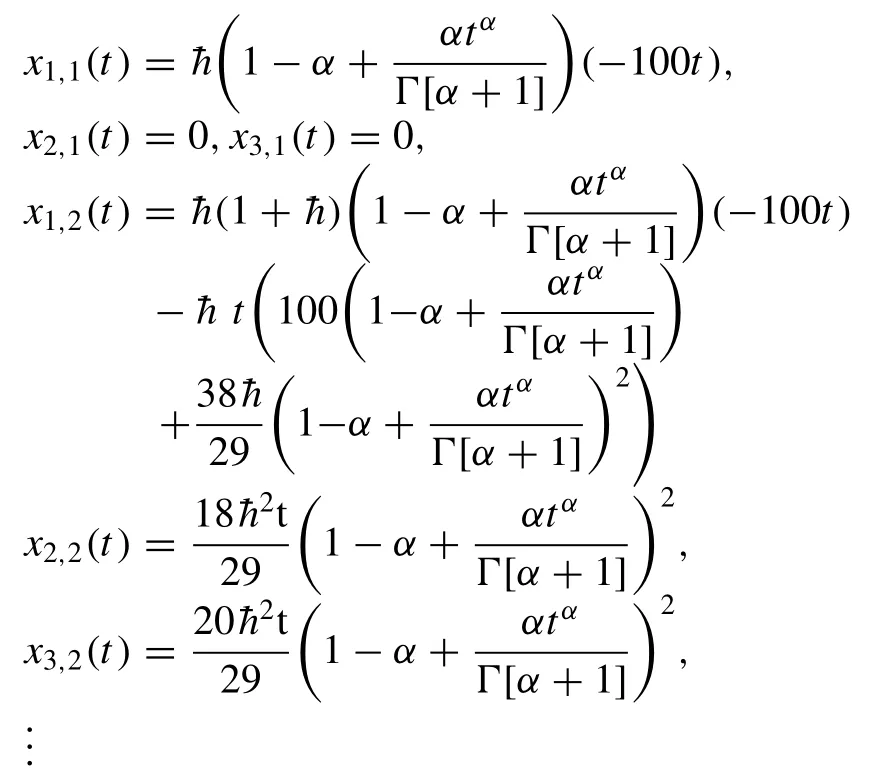
Here, we illustrated the behaviour of theq-HATM solu- tion obtained for the system of fractional order differential equations exemplifying the Lakes pollution model with the aid of the proposed scheme.The fourth-order iterated solu- tion has been considered to present the behaviours and its corresponding consequence.The behaviour of the proposed model cited in Case 1 for distinct fractional order in captured in Fig.2 .The response of the series solution for periodic input model in presented in Fig.3 .For the exponentially de- caying input model, the response ofq-HATM solution for diverseαis illustrated in Fig.5 and similarly for linear input model in presented in Fig.7 .The ? -curves are drowned for diverseμto analyse the behaviour of theq-HATM solution for the considered model cited in three cases with homotopy parameter ( ? ), and which respectively presented in Figs.4 , 6 and 8 .Further, these plots help us to control and regu- late the convergence region for theq-HATM solution.Theq-HATM solution quickly converges to the analytical solu- tion for a suitable value of ? .In this connection, recently authors in [60–63] consider a very effective and simple pro- cedure to evaluate the appropriated value of ? in order to rapid convergence.

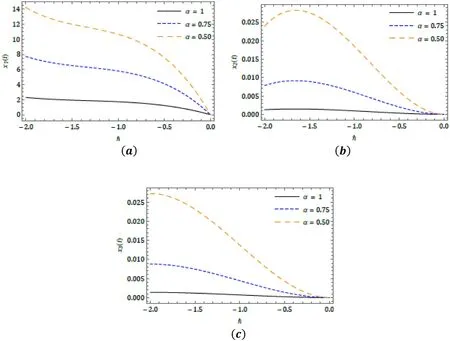
Fig.8.? -curves for ( a ) x 1 ( t ), ( b ) x 2 ( t ) and ( c ) x 3 ( t ) with distinct α at n = 1 and t = 0. 01 for the Case 3.

From all the plots we can see that the illustrated model conspicuously depends on arbitrary order, and further from these plots, we can able capture the dynamical behaviour of the considered system.The small variation in the physical be- haviour in these types of models exhibits the most interesting consequences to understand and predict nature in a systematic and better fashion.From the obtained results, we can see that the considered scheme is very efficient to examine the sys- tem of fractional differential equations describing the Lakes pollution.

7.Conclusion

In this study, we analysed and capture the behaviour of the considered model with the help of a fractional operator.Since the generalized Mittag-Leffler function is non-singular and non-local kernel in nature and it is considered to de- fine fractional-order AB derivatives, the present study proves its efficiency while analysing the real word problems.With the help of fixed point theorem for the obtained solution, we demonstrated the existence and uniqueness.More precisely, the considered technique finds the solution for the proposed system without making any transformations, perturbation or discretization.From the capture plots, we can see that the con- sidered model is highly dependent on the fractional operator and parameters offered by the projected method, and further effectively analysed in the present framework.The results ac- complished by the proposed methods are more interesting as related to already available results.The current study eluci- dates, the proposed Lakes pollution model remarkably depend on time instant and its history, and which can be persuasively exemplified using the fractional concept.The present frame- work can help the young scholars to analyse the behaviour of the various models, and also gives very useful and interesting consequences.