唐保祥, 任 韓

(1. 天水師范學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 甘肅 天水 741001； 2. 華東師范大學(xué) 數(shù)學(xué)系, 上海 200062)

1 引言與預(yù)備知識(shí)

對(duì)于圖完美匹配的計(jì)數(shù), 目前已有一些精巧的計(jì)數(shù)方法[1-4], 但還沒(méi)有一般的方法求一般圖完美匹配的數(shù)目. 文獻(xiàn)[5-8]研究表明, 對(duì)于一些特殊圖, 把所研究的圖按照匹配某個(gè)頂點(diǎn)的完美匹配分類(lèi), 先求出每一類(lèi)完美匹配數(shù)目的遞推關(guān)系式, 即可得所研究圖的完美匹配數(shù)目計(jì)數(shù)公式.

定義1如果圖G有一個(gè)1-正則生成子圖, 則稱(chēng)該生成子圖為圖G的完美匹配.

定義2設(shè)S1,S2是圖G的兩個(gè)完美匹配, 如果S1和S2中有一條邊不同, 則稱(chēng)S1和S2是圖G兩個(gè)不同的完美匹配.

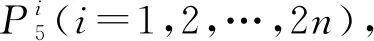
圖1 圖2-2nP5

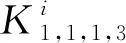
圖2 圖2-nK1,1,1,3

2 主要結(jié)果

定理1令η(2n)是圖2-2nP5的完美匹配數(shù), 則

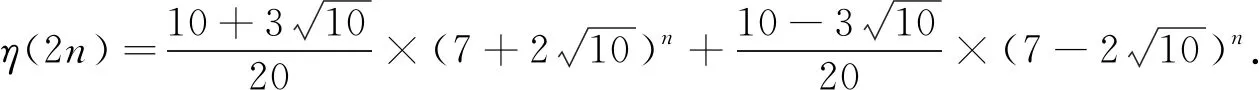
(1)

證明: 圖2-2nP5顯然存在完美匹配. 要求函數(shù)η(2n)的解析式, 先要定義圖G1并求出其完美匹配數(shù)的遞推式. 把路pq的端點(diǎn)p,q分別與圖2-2nP5的頂點(diǎn)u11,u13連接一條邊產(chǎn)生的圖記為G1, 如圖3所示. 由圖3可見(jiàn), 圖G1存在完美匹配, 用μ(2n)表示圖G1的完美匹配數(shù). 設(shè)圖G1完美匹配的集合為P, 圖G1含有邊pq,pu11的完美匹配集合分別為P1,P2, 則P1∩P2=?,P=P1∪P2, 故μ(2n)=|P|=|P1|+|P2|. 因?yàn)閜q∈P1, 所以pu11,qu13?P1, 故由η(2n)的定義知, |P1|=η(2n).

圖3 圖G1

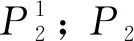
μ(2n)=η(2n)+η(2(n-1))+μ(2(n-1)).

(2)

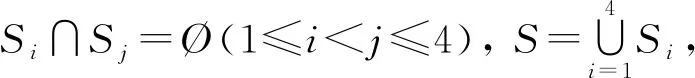
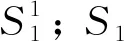
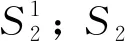
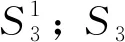
|S3|=4η(2(n-1))+μ(2(n-1)).

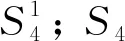
綜上, 有

η(2n)=11η(2(n-1))+2μ(2(n-1)).

(3)

由式(2)得

μ(2(n-1))=η(2(n-1))+η(2(n-2))+μ(2(n-2)),

(4)

把式(4)代入式(3), 得

η(2n)=13η(2(n-1))+2η(2(n-2))+2μ(2(n-2)).

(5)

由式(3)得

η(2(n-1))=11η(2(n-2))+2μ(2(n-2)),

(6)

將式(5),(6)消去μ(2(n-2)), 得

η(2n)=14η(2(n-1))-9η(2(n-2)).

(7)

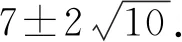
其中c1,c2為待定常數(shù). 圖4為圖2-2×1P5的完美匹配. 由圖4知,η(2×1)=13,μ(2×1)=15. 從而由式(3)得η(2×2)=173. 故式(1)成立.

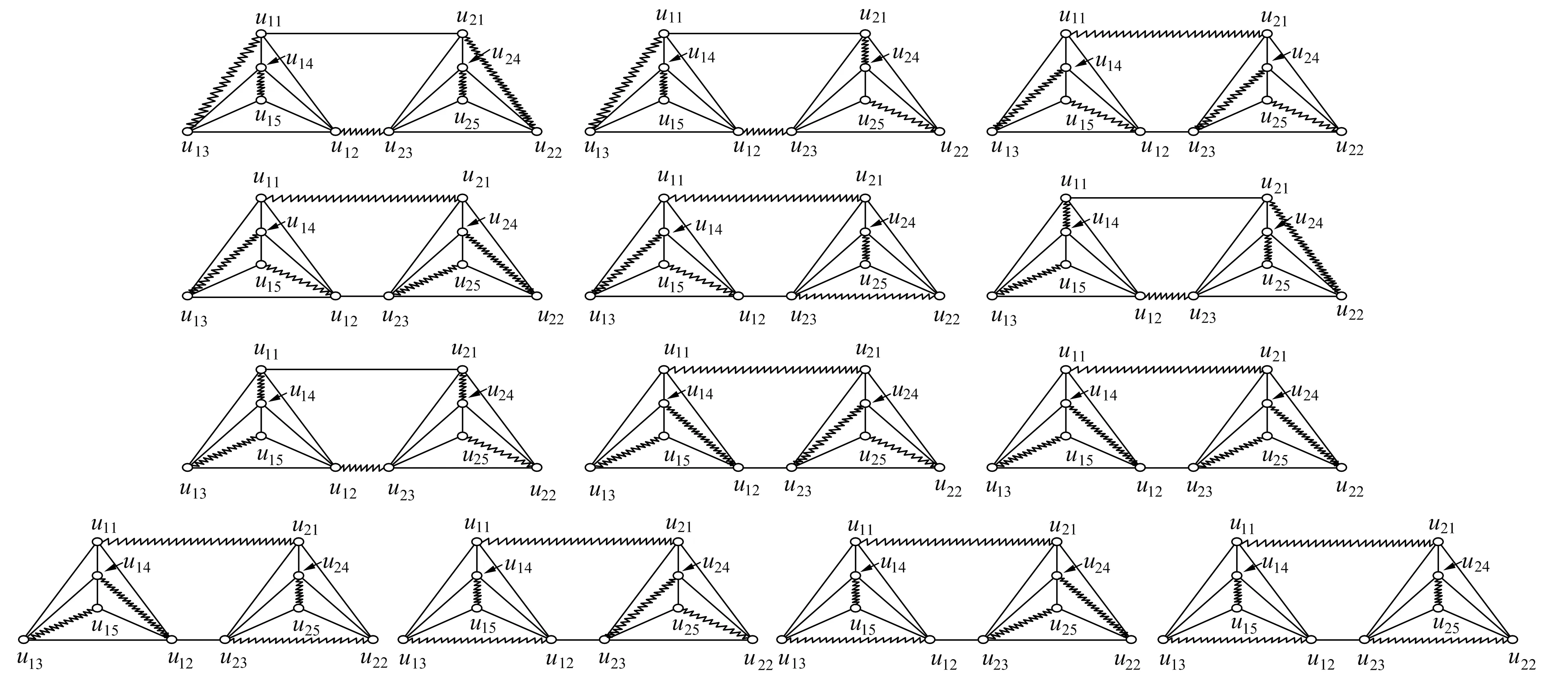
圖4 圖2-2×1P5的完美匹配

定理2令λ(n)為圖2-nK1,1,1,3的完美匹配數(shù), 則

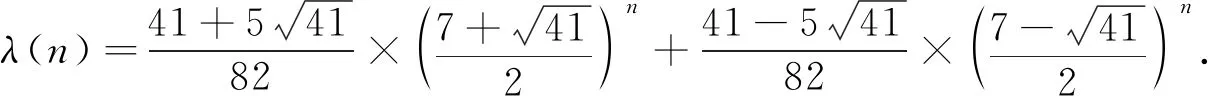
(8)

證明: 圖2-nK1,1,1,3顯然存在完美匹配. 要求函數(shù)λ(n)的解析式, 先要定義圖G2并求出其完美匹配數(shù)的遞推式. 把路wt的端點(diǎn)w,t分別與圖2-nK1,1,1,3的頂點(diǎn)u11,v11連接一條邊生成的圖記為G2, 如圖5所示. 由圖5可見(jiàn), 圖G2有完美匹配, 用π(n)表示圖G2的完美匹配數(shù). 設(shè)圖G2完美匹配的集合為S, 圖G2含有邊wt,wu11的完美匹配集合分別為S1,S2, 則S1∩S2=?,S=S1∪S2, 從而π(n)=|S|=|S1|+|S2|. 因?yàn)閣t∈S1, 所以wu11,tv11?S1, 故由λ(n)的定義知, |S1|=λ(n).

圖5 圖G2

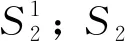
π(n)=λ(n)+λ(n-1)+π(n-1).

(9)

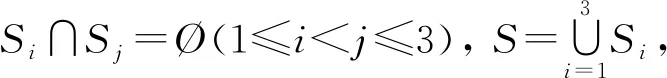
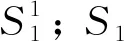
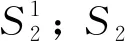
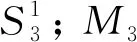
λ(n)=4λ(n-1)+2π(n-1).

(10)

由式(9)得

π(n-1)=λ(n-1)+λ(n-2)+π(n-2),

(11)

把式(11)代入式(10), 得

λ(n)=6λ(n-1)+2λ(n-2)+2π(n-2).

(12)

由式(10), 得

λ(n-1)=4λ(n-2)+2λ(n-2),

(13)

將式(12),(13)消去π(n-2), 得

λ(n)=7λ(n-1)-2λ(n-2).

(14)

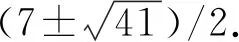
其中c1,c2為待定常數(shù). 圖6為圖2-1K1,1,1,3的完美匹配. 由圖6知,λ(1)=6. 圖7為圖G3的完美匹配, 由圖7知,π(1)=8. 從而由式(10)得λ(2)=40. 故式(8)成立.

圖6 圖2-1K1,1,1,3的完美匹配

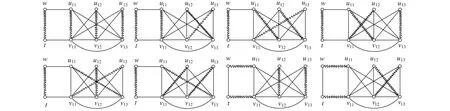
圖7 圖G3的完美匹配