SUN Ding,DING Yanyan,KONG Lingwei,ZHANG Yuhong,GUO Xiujuan,WEI Liming,ZHANG Li,ZHANG Lixin

(1. School of Physics,Nankai University,Tianjin 300071,China; 2. School of Electrical and Computer Engineering,Jilin Jianzhu University,Changchun 130118,China; 3. School of Materials Science and Engineering,Jilin Jianzhu University,Changchun 130118,China; 4. Institute of Photo Electronics thin Film Devices and Technology,Nankai University,Tianjin 300071,China)

Abstract: To date,solar cells with efficiency of 12.6% has been demonstrated via a hydrazine-based solution approach. Despite this progress,performance of Cu2ZnSn(S,Se)4 solar cells remains far lower than the Shockely-Quiser theoretical limit. We performed density functional theory calculations with hybrid functional approach to investigate the Mg-related defects in the kesterite structure of the Cu2ZnSnS4 (CZTS) solar cell material. The substitution energies of Mg atom in CZTS were calculated in consideration of the atomic chemical potentials of the constituent elements of Cu,Zn,Sn,and the doping atom of Mg. From our calculation results,Mg doping in CZTS under certain Sn-rich growth condition is expected to convert the conduction from p-type to n-type. The present study provides a theoretical basis for exploring practical applications of Mg doping in CZTS solar cells.

Key words:kesterite; Mg; first-principle; solar cell

The kesterite Cu2ZnSn(S,Se)4(CZTSSe) based compound solar cells has attracted a great number of attentions because of the non-toxicity and abundance of the constituent elements[1]. To date,solar cells with efficiency of 12.6% was demonstratedviaa hydrazine-based solution approach[2]. Despite this progress,performance of CZTSSe solar cells remains far lower than the Shockely-Quiser theoretical limit[3]. The existence of abundant antisite defects (CuZnor ZnCu) in the CZTSSe absorber are considered to be an important factor that deteriorates the solar cell performances[4]. Therefore,a wide variety of research has been done to find the alternatives for kesterite CZTSSe and an approach to substitute other elements for Cu or Zn to suppress the formation of antisite defects and thus improve the device performance. Substitution of Cd,Fe and Mn for Zn to form Cu2CdSnS4[5],Cu2FeSnS4[6]and Cu2MnSnS4[7]thin film and Cr doping[8]had been experimentally achieved. Whereas,these elements are toxic and may bring undesirable magnetism into device.By contrast,Mg element is environmentally friendly,and Mg-doped ZnO window layer was used in CIGS thin film solar cell to improve short circuit current[9].

Recently,Mg-doped CZTS(Se) materials have been synthesized by many techniques such as ultrasonic co-spray method[10],pulsed laser deposition method (PLD)[11],and a liquid-phase reactive sintering technique[12]. In these works,structural,electronic and optical properties of Mg-doped CZTS(Se) were studied. Nevertheless,Mg-doped CZTS deposited by PLD showed p-type conductivity behavior while Mg-doped CZTSe prepared by reactive sintering technique exhibited n-type electrical conductivity. To the best of our knowledge,no experimental or theoretical work has been done to clarify which element in CZTS(Se) is more likely substituted by Mg and what kind of defects might be introduced into CZTS(Se) by Mg doping. Rapidlydeveloping first-principles calculation methods make it possible to study substitution of Zn in CZTS(Se) theoretically[13-15]. Therefore,in this work we studied the formation energies of Mg impurities in kesterite CZTSviahybrid functional calculations. On the basis of our results,we identified the energetics of the most likely positions in CZTS for the incorporation of Mg extrinsic defects,which may help improving the further application of CZTS(Se) solar cells.

1 Computational details

In the present work,all calculations have been performed based on density functional theory (DFT) as implanted in the VASP code[16]. The interaction between ions and electrons is described by the projector augmented wave (PAW) method[17]with a plane-wave cutoff energy of 400 eV. For defect calculations,a 2×2×1 supercell containing 64 atoms is adopted,as shown in Fig. 1. A 2×2×2 Monkhorst-Pack k-point mesh is used for the Brillouin-zone integration of the 64-atom cell.

Screened Coulomb hybrid functional Heyd-Scuseria-Ernzerhof (HSE06)[18]is used to calculate the electronic structures and defect properties. The range-separation screening parameterμis set to 0.02 nm-1and the amount of Hartree-Fock exchange is set to 0.25 in the HSE06 functional. Our calculations are done in two steps. In the first step we optimize the atomic structure by using GGA in the Perdew-Burke-Ernzerhof (PBE) form[19]. In this step,the lattice parameters were optimized through the minimization of total energy. In the second step we do the static electronic calculation by the HSE06 hybrid functional. All lattice vectors and atomic positions were fully relaxed by minimizing the quantum mechanical stresses and forces. It shows that the band gap obtained by this two-step procedure is in excellent agreement with the experimental value in previous work[20]. These parameters and methods ensure the calculated band gap for CZTS close to the experimental values.

Mg-related point defects including three antisites MgCu,MgZnand MgSnare considered (one Mg atom substitutes Cu,Zn and Sn site,respectively). The defect formation energies are calculated as[21]

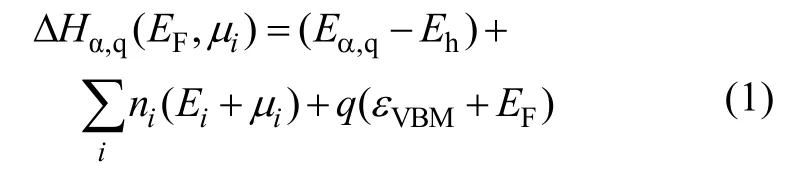
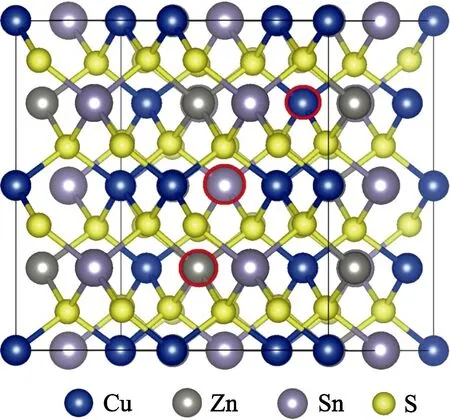
Fig. 1 Supercell used to calculate the defect properties ofMg-doped CZTS,where the red circles denote the locations of the antisite defects

whereEα,qandEhis the total energy of the supercell with and without a defect α,respectively.Eiis the total energy of the component elementiin its pure phase;niis the number of atomsiremoved from the supercell in forming the defect with the chemical potentialμiin forming the defect α. Theμiis referenced to the total energyEiof the elemental solid andμi=0 means the element is so rich that the pure element phase can form.EFis the Fermi energy,which varies from valence band maximum (VBM) of the host,denoted byεVBM,to the conduction band minimum (CBM) for non-degenerate semiconductors. Because of the finite size of supercells,the Lany and Zunger correction method[22]is used to correct the image-charge interaction with a relative dielectric constant (εr) of 8.1[23]of the monopole correction.And potential alignment correction is applied by aligning the core-averaged electrostatic potentials far from the defect[24].

2 Results and discussion

The predicted lattice parameters and bandgap results by using two types of exchange-correlation functionals are presented in Table 1. HSE06 functional predicts a bandgap of 1.45 eV for CZTS,in consistent with the experimental values. By contrast,the PBE functional largely underestimate the bandgap. Therefore,HSE06 is used to calculate the electronic structures and defect properties of Mg-doped CZTS.

A defect often produces states within the band gap,with the stronger the gap states,the more localization of the defect charge distribution. The charge localization feature can be seen from the band structures,as shown in Fig. 2. The charge states of MgCuand MgSnare similar to ZnCuand ZnSnwhich are both charge delocalized defects[26]. For these defects,defect-induced states hybridize with the conduction band or the valence band and are difficult to be separated,thus there is invisible defectinduced levels within the band gap[27]. The electrons on these charge delocalized defects are loosely bounded and easy to be ionized and will not produce deep defect levels within the band gap.

Whether a defect level could significantly affect the solar cell performance also depends on its concentration which is related to the formation energy,a function of the elemental chemical potentials and Fermi level according to eq. (1). And the stable region of chemical potential is needed to be determined before performing the calculationof formation energies of the Mg-related defects. A series of thermodynamic conditions must be satisfied by the chemical potentials:

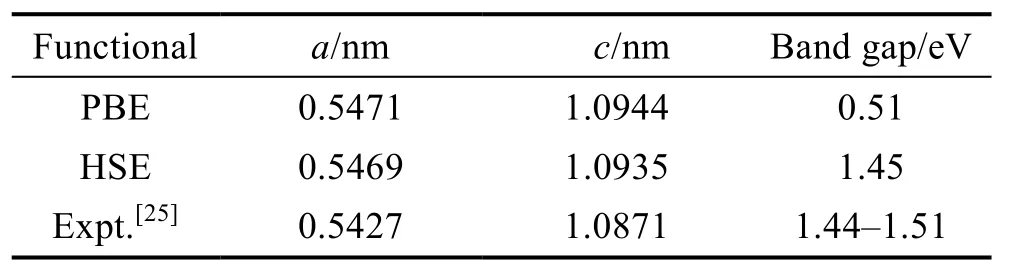
Table 1 Lattice parameters a and c and band gaps of CZTS as obtained using PBE and HSE compared to experimental values

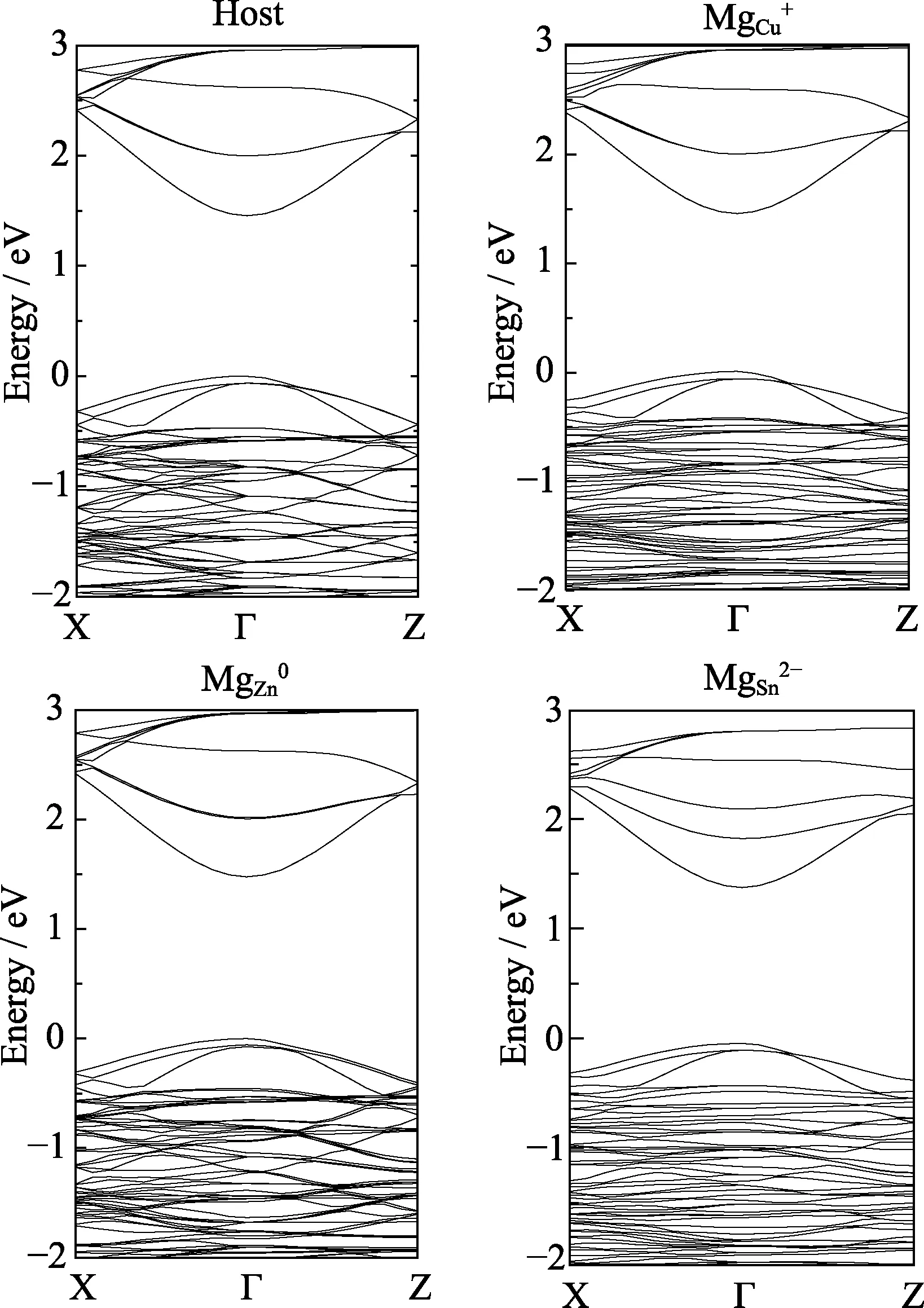
Fig. 2 Band structures of the host CZTS and the MgCu,MgZn and MgSn with different charge states

(I) The sum of the chemical potentials of the component elements should maintain a stable host compound,which means:

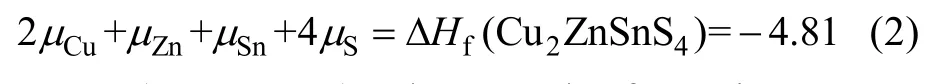
where ΔHf(Cu2ZnSnS4)relates to the formation energy of Cu2ZnSnS4.

(II) The formation of pure elemental phase should be avoided. Thus,the atomic chemical potentials in CZTS should be smaller than that of the corresponding elemental solid. That is:

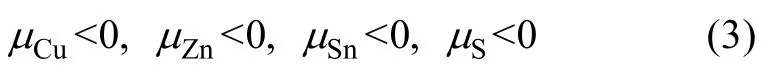
(III) The formation of all other secondary compounds including CuS,Cu2S,ZnS,SnS,SnS2,Cu2SnSe3and MgS should be avoided,as described by the following relations:

With the thermodynamic conditions established,the stable chemical potential region of CZTS is confined in a three-dimensional space. As a result of Equation 2,there can be only three independent variables for CZTS,such asμCu,μZnandμSn. Here we take the chemical potential range determined by Zhanget al.[28]for CZTS. When Mg induced secondary phase MgS is considered,the stable chemical potential region is surrounded by ABCD,as shown in Fig. 3. The chemical potential values for each element at points A-D are listed in Table 2. Point D is more Zn-rich in growth condition compared to that of points A-C.

To figure out the microscopic mechanism of Mg-doping,the formation energies as a function ofEFfor Mg-related defects at points A-D are calculated. Whereas we only show the results at point D since Zn-rich growth condition is preferred by CZTS solar cells with high efficiency.As shown in Fig. 4,the formation energies of MgCu+and MgZn0are lower than 2 eV in the wholeEFrange,which means these defects can exist in large amount in CZTS.By contrast,the formation energy of MgSn2-is higher than 2 eV whenEFis closed to the VBM.

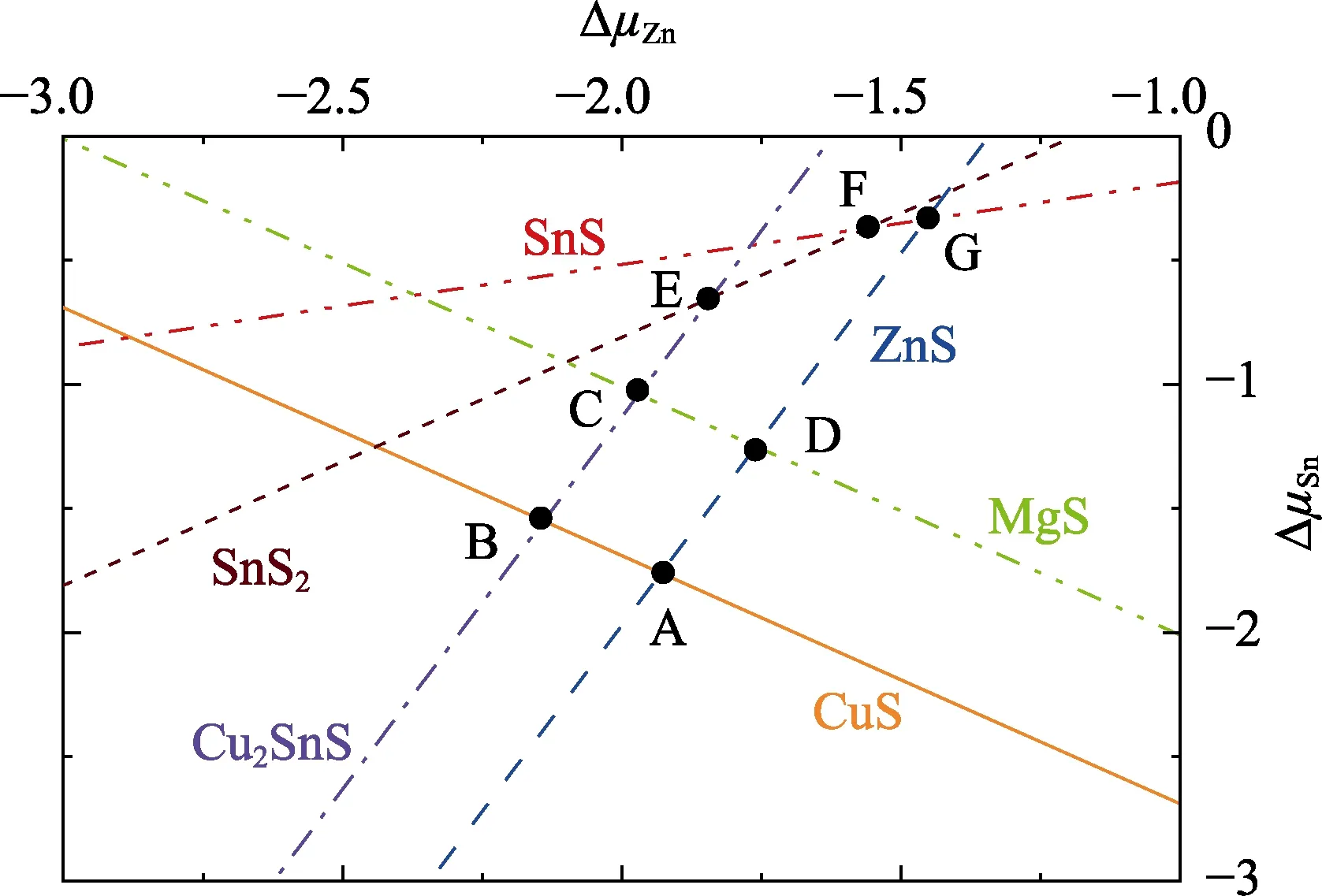
Fig. 3 Stable chemical potential region of CZTS(considering the Mg induced secondary phase MgS) with μCu = -0.5 eV

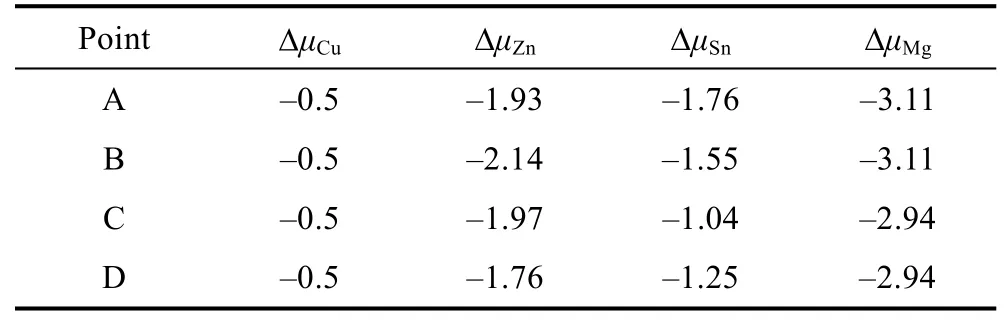
Table 2 Chemical potentials at the A-D points labeled in Fig. 3/eV

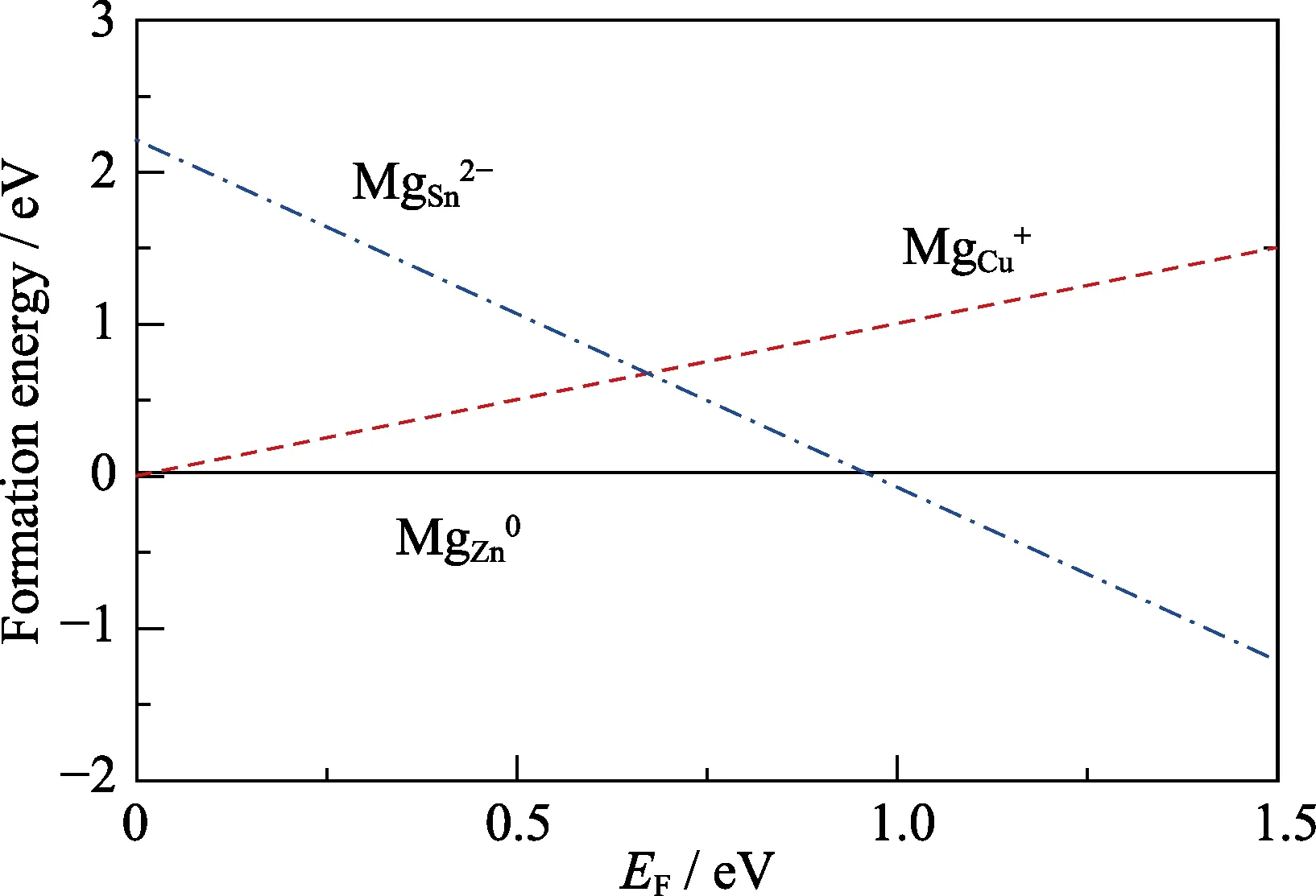
Fig. 4 The formation energies of Mg-related defects as a function of Fermi energy at point D shown in Fig. 3

It is also found that the formation energy of MgZn0is even smaller than that of MgCu+in largeEFrange,which indicates that the Mg atom prefers to substitute the Zn atomic site in CZTS. Since Mg and Zn are isovalent,the MgZnwill not affect the conduction type. Moreover,the existence of MgZnmakes it easy for other Cu atoms to be substituted by Mg atom. The comparison of the formation energy of MgCuin the supercell with and without a Mg dopant on the Zn site is shown in Fig. 5. With Mg dopant,the formation energy of MgCu+decreases by 52 meV than that without Mg atom. The Bader charge shows that the amount of transferred electron from Mg to S is larger than that of Zn in CZTS,as shown in Fig. 6.Thus,it compensates electrons transferred from other Cu atoms to obey the Octet rule which makes the Coulomb attraction between Cu-S weaker than that in pure CZTS.As a result,it is easier for Cu atom to be substituted by Mg atom,and Mg doping promotes the population of MgCudonor.

A buried p-n junction in Cu(InGa)Se2(CIGS) film facilitates electron-hole separation of photogenerated carriers. Some groups attempted doping of Cd into CIGS films to convert the near-interface region from p-type CIGS to n-type to improve the performances[29]. However,intentional doping of CZTS to n-type through extrinsic elements is challenging,and may be one reason CZTS suffers from poor efficiencies[30]. In addition to nontoxicity of Mg element,MgCudonor has a relatively low formation energy which can be further lowered with the existence of MgZn. Therefore,we propose the doping of Mg at the CZTS surface need to be further studied by a theoretical and experimental approach. Besides the Cu-poor and Zn-rich condition which are preferred in the high efficiency solar cells,previous work[26]has discussed that Sn-rich growth condition is important in the CZTS synthesis procedure to suppress CuSn. We propose the Sn-rich growth condition is also important to suppress MgSnwhenEFis close to the CBM. As a result,Mg prefers to substitute the Cu atomic site and acts as shallow donor in CZTS. Hence,Mg is a promising dopant to further improve the performance of Cu2ZnSnS4-based solar cell.

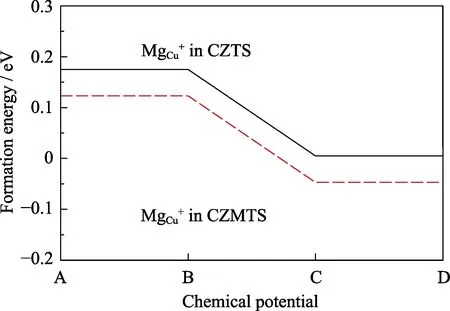
Fig. 5 The comparison of the formation energy of MgCu in pure CZTS and Mg doped CZTS as a function of chemical potential at points A,B,C and D shown in Fig. 3

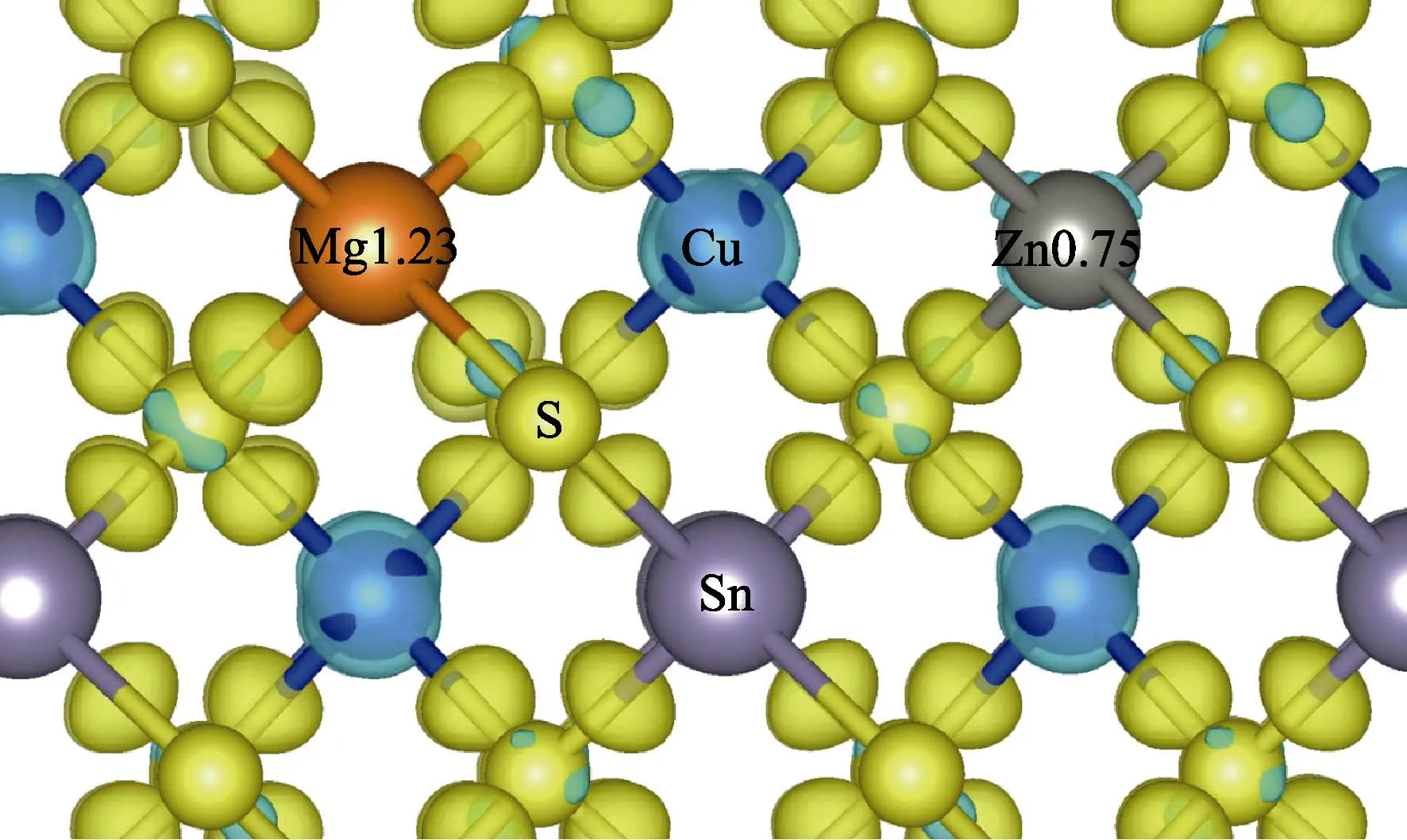
Fig. 6 The difference density charge (including Bader charges)for Mg doped CZTS

3 Conclusions

In this work,we have carried out hybrid functional computations on the Mg-related defect properties in CZTS. According to our results,all Mg-related defects are not charge localized defects and will not produce deep defect levels within the bandgap. Furthermore,MgCuand MgZnhave very low formation energies in largeEFrange. Besides the well-established Cu-poor and Zn-rich growth conditions,Sn-rich growth condition is proposed to suppress MgSn. Under these conditions,Mg prefers to occupy the Cu atomic site and acts as shallow donor. Finally,we suggest that Mg doping on the surface might be an effective method to further improve the efficiency of Cu2ZnSnS4-based solar cells.