Sicong Liu,Xiao Huang

Department of Information&Communication Engineering,School of Informatics,Xiamen University,Xiamen 361005,China

Abstract:The deep convolutional neural network(CNN)is exploited in this work to conduct the challenging channel estimation for mmWave massive multiple input multiple output(MIMO)systems.The inherent sparse features of the mmWave massive MIMO channels can be extracted and the sparse channel supports can be learnt by the multi-layer CNN-based network through training.Then accurate channel inference can be efficiently implemented using the trained network.The estimation accuracy and spectrum efficiency can be further improved by fully utilizing the spatial correlation among the sparse channel supports of different antennas.It is verified by simulation results that the proposed deep CNN-based scheme significantly outperforms the state-of-the-art benchmarks in both accuracy and spectrum efficiency.

Keywords:deep convolutional neural networks;deep learning;sparse channel estimation;mmWave massive MIMO

I.INTRODUCTION

Massive multiple input multiple output(MIMO)has been adopted as a key alternative in 5G wireless communications since it can significantly increase the data rate and spectral efficiency[1].However,channel estimation for massive MIMO and millimeter wave(mmWave)massive MIMO systems[2,3]becomes much more challenging since the overhead of time and frequency resources dramatically increase with the number of antennas[4,5].Exploiting the sparse nature of wireless channels,i.e.the channel impulse response(CIR)is concentrated on only a few dominant taps in the delay domain while most entries are approximately zero[5–7],some compressed sensing(CS)-based methods have been proposed to reduce the overhead and improve the performance for both massive MIMO channels[8]and mmWave massive MIMO channels[9,10].Still in severe conditions,e.g.in the low signal-to-noise ratio(SNR)region or in case of insufficient measurement data,the estimation accuracy is limited.

Inspired by the emerging technology of deep learning,several effective deep neural networks have recently been proposed to solve sparse recovery problems.Based on the conventional recursive method,the conventional iterative recovery algorithms with good interpretability,e.g.the iterative shrinkage thresholding algorithm(ISTA)[11],can eventually obtain the globally optimal solution of sparse approximation problems.By unrolling the iterations of ISTA into a multi-layer neural network,the learned ISTA network(LISTA)[12]is proposed to mimic the repeated sparse approximation process of ISTA.An improved method of ISTA-Net casts the ISTA into an enhanced deep neural network architecture,where the convolutional neural network(CNN)is employed to extract a better sparse representation of the signal of interest[13].

Recently,some deep learning-based methods have been incorporated in the estimation of both massive MIMO and mmWave massive MIMO channels.For massive MIMO systems,deep learning is applied to estimate the uplink channels for massive MIMO with mixed-resolution analog-to-digital converters in[14].A deep learning-based framework is proposed for direction-of-arrival estimation and massive MIMO channel estimation[15].A two-stage massive MIMO channel estimation process is proposed based on deep learning,including pilot-aided and data-aided estimation stages[16].A massive MIMO channel estimator is jointly designed with pilot signals based on deep learning[17].For mmWave massive MIMO systems,on the other hand,a learned denoising-based approximate message passing(LDAMP)network is proposed to estimate the beamspace mmWave massive MIMO channel[18].The frequency correlation among channels at adjacent subcarriers is exploited in[19]for mmWave massive MIMO channel estimation using a CNN network.

In fact,the CNN network can be utilized better to extract the sparse feature of the delay-domain wireless channel supports.Besides,due to the spatial correlation of the sparse structure among the channel supports of different antennas,the CIRs of different antennas share a sparse common support[6,7].Actually,the spatial correlation might bring considerable benefit for the estimation performance of mmWave massive MIMO channels,which remains to be well exploited.Thus in this work,a novel deep learning and deep CNN-based mmWave massive MIMO channel estimation scheme is proposed.The inherent sparse structure of the wireless channel is effectively extracted by the CNN structure in each layer of the deep network.Moreover,the spatial correlation among a large number of antennas is also fully exploited to improve the estimation accuracy and spectrum efficiency.The main contributions of this work are summarized as follows:

? Accurate and efficient channel inference can be achieved using the well-trained deep CNN-based network,which can effectively extract the inherent sparse features of mmWave massive MIMO channels and reconstruct the channel support.

? The estimation accuracy of the sparse channel support is further refined by fully exploiting the spatial correlation among different MIMO subchannels,i.e.a refined common channel support is derived by the intersection of all the inferred supports for different antennas.

Simulation results demonstrate that the proposed scheme can significantly improve the accuracy of mmWave massive MIMO channel estimation,especially in case of low SNR or insufficient measurement data,i.e.frequency-domain pilots,compared with the state-of-the-art benchmark schemes,including the conventional least squares(LS),compressed sensing,and deep learning based methods.Furthermore,since the channel estimation process in practice is conducted by only one feed-forward operation flow exploiting the already well-trained networks,the proposed method is very applicable for practical mmWave communication user equipment.

The structure of this work is as follows.Related works are summarized in Section II.The system model is presented in Section III.The deep CNN-based mmWave massive MIMO channel estimation scheme is proposed in Section IV.Simulation results are given in Section V,followed by the conclusions.

The frequently used abbreviations and terminologies in this paper are listed in Table 1.

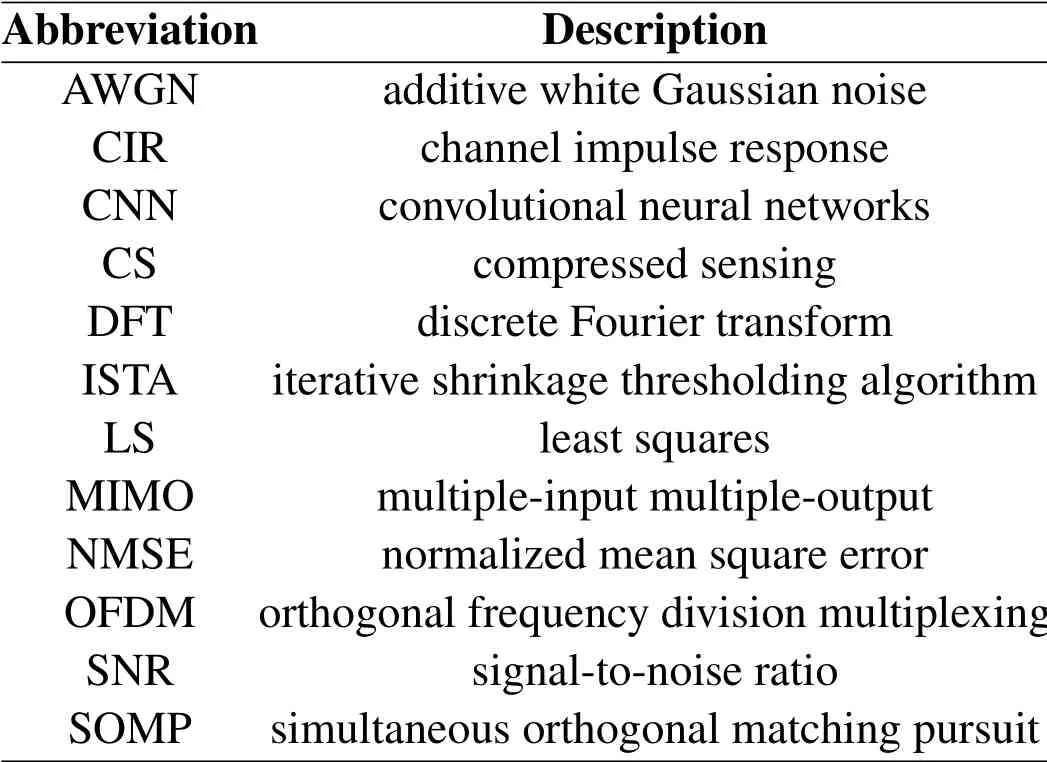
Table 1.List of abbreviations.

Notation:Matrices and column vectors are denoted by boldface letters;frequency-domain and timedomain vectors are denoted by boldface vectors with tildeand without tilde v,respectively;The superscript(t)to a vector v(t)denotes that the vector is related with thet-th transmit antenna;denotes the set of complex number;(·)?,(·)Tand(·)Hdenote the pseudo-inversion,transpose and conjugate transpose operations,respectively;AΠrepresents the sub-matrix comprised of the columns of the matrix A indexed by the set Π.

II.RELATED WORKS

As the number of antennas involved with the channels to be estimated in massive MIMO systems is large,the CS theory has been utilized to decrease the pilot consumption overhead effectively.A spatially non-stationary channel model is adopted to capture the delay-domain sparse characteristics of the massive MIMO channels,and block matching pursuit algorithm is used for massive MIMO channel estimatoin[5].Qiet alprovides an analysis of the block coherence of massive MIMO channels and proposes an improved sparse channel estimation scheme in the framework of CS[20].Based on auxiliary information of the massive MIMO channels,an auxiliary block subspace pursuit algorithm is proposed to reconstruct the massive MIMO channel[21].

To improve the estimation accuracy in massive MIMO systems,some effective sparse channel estimation approaches have been proposed exploiting the spatial correlation,i.e.the sparse common support,among the multiple antennas.The sparse common support property is exploited to estimate the massive MIMO channels in the delay domain in[6].An adaptive channel estimation scheme based on spatially common sparsity is investigated to achieve an enhanced performance of channel state information acquisition for massive MIMO channels[22].A doubly sparse approach for mmWave massive MIMO channel estimation is proposed to improve the estimation accuracy greatly with affordable complexity[23].

Recently,the methods based on deep learning have drawn plenty of attention from the research community,and are also being introduced to the area of channel estimation of massive MIMO to achieve a better performance.A deep learning based scheme focused on massive MIMO channel estimation is proposed in[15],where deep neural networks are utilized to learn the statistics of the wireless channel in the angle domain.A channel estimation algorithm for doubly selective fading channels is proposed,which employs deep neural networks to facilitate channel estimation[24].A deep-learning-based channel estimation scheme called ChanEstNet is designed in[25]for high speed scenarios,where convolutional neural networks are employed to extract the channel response feature vectors,and recurrent neural networks are used to have a better track of the features of the fast varying channels.Besides,since a layer-by-layer training method is employed,only a small proportion of the parameters need to be updated for each new layer of network during training.

III.SYSTEM MODEL

A mmWave massive MIMO transmission system is considered in this work as illustrated in Figure 1.It is equipped withNtantennas at the transmitter,e.g.a base station,andNrantennas at the receiver,e.g.a mobile user equipment,whereNrcan also be one for scenarios like multi-user MIMO(MU-MIMO)[8].The length-LCIR h(t)∈Lbetween thet-th transmit antenna and a certain receive antenna,without loss of generality,can be modeled as

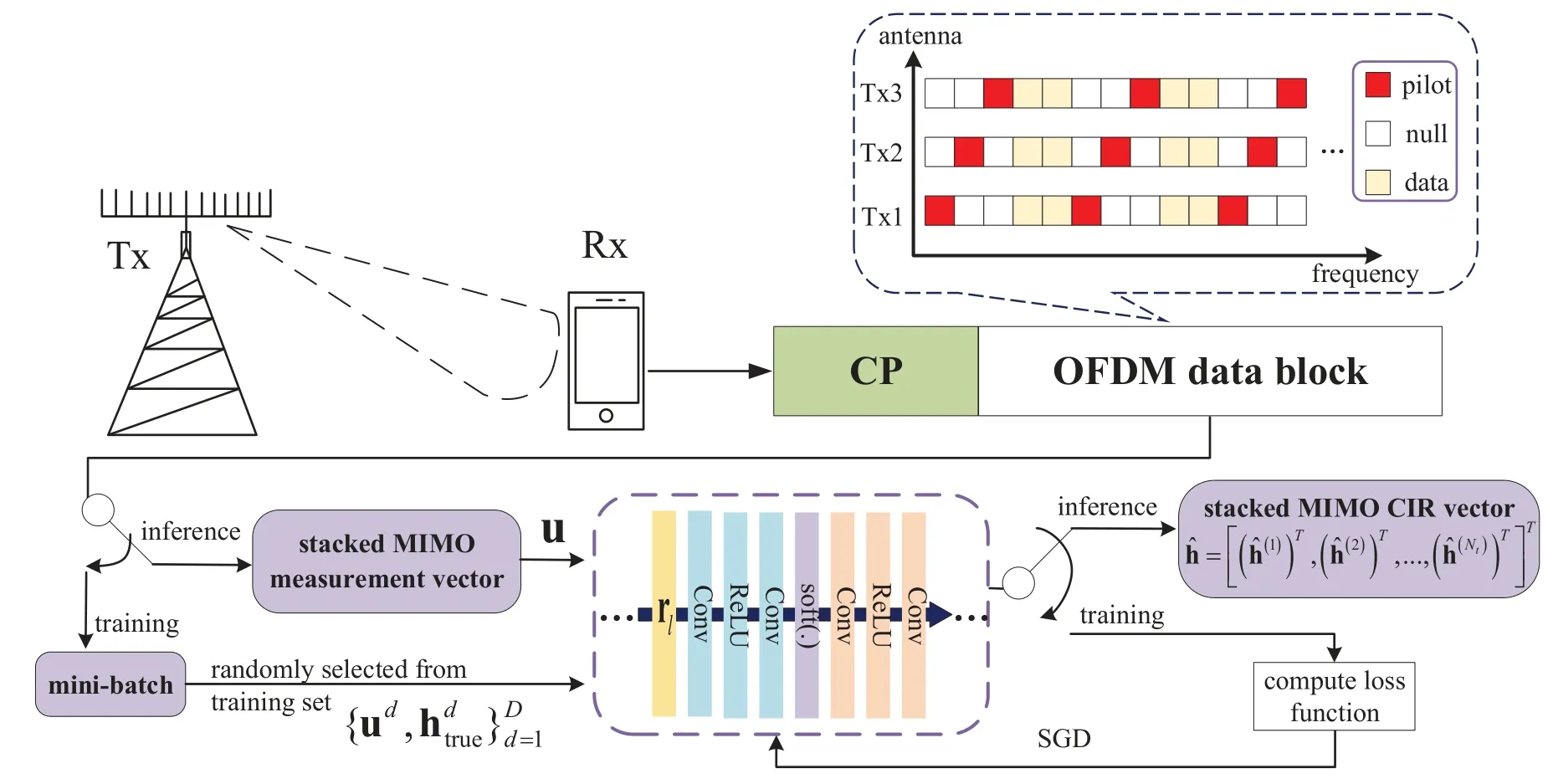
Figure 1.The signal model and architecture of the proposed deep CNN-based channel estimation scheme for a mmWave massive MIMO system.

Due to the propagation characteristics of outdoor environment,most of the energy of a wireless channel is concentrated on a few dominant taps,making the channel CIR a sparse or approximately sparse vector[6,26,27].Note that the sparse channel is modeled in the delay-domain,i.e.the CIR vector h(t)is representing a delay-domain sparse channel.This wireless channel is modeled based on the parametric sparse channel model given in[26].Specifically,the sparsity of the CIR follows a parametric sparsity-promoting Bernoulli-Gaussian prior distribution.That is,the support of the CIR vector,i.e.the location of nonzero entries,is randomly determined and follows an i.i.d.Bernoulli distribution,with each entry of the CIR vector having an identical probability to be nonzero or zero.If a CIR entry is nonzero subject to the Bernoulli distribution,then it contributes a nonzero channel tap,whose amplitude is determined by a zero-mean Gaussian distribution[26].In addition,according to the model[26],the parametric sparse channel with uncorrelated-scattering assumption is effective for specular sparse channels,approximately sparse channels and dense channels.Apart from the delay-domain sparse channel model described above,the Saleh-Valenzuela(S-V)model is also used in many cases for mmWave massive MIMO systems[28,29].The angle-domain sparsity can be conveniently represented by this model and exploited for sparse channel estimation[10,30].The proposed method is also applicable to the problem formulated by this model,which can be conducted similarly by measuring and learning the angle-domain sparsity instead of the delay-domain sparsity of the channel.

A certain OFDM signal model sent by thet-th transmit antenna consists of the length-Mcyclic prefix(CP)and the length-NOFDM data blockgiven by

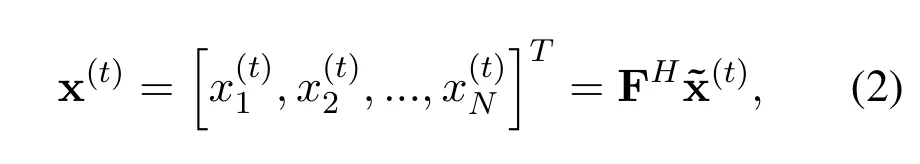
where F is theN × Ndiscrete Fourier transform(DFT)matrix withNbeing the sub-carrier number.denotes the OFDM data block in frequency domain,andNppilots are randomly distributed over the OFDM sub-carriers.The locations of these pilots are denoted by a setD(t)given by

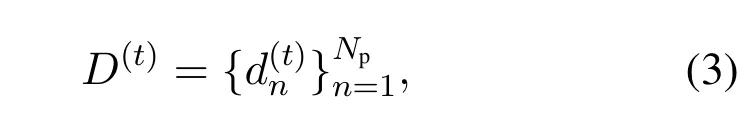
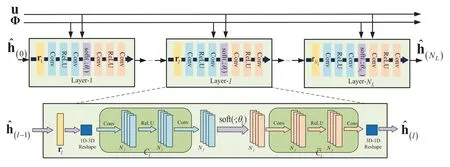
Figure 2.The structure of the l-th layer in the proposed CNN-based network for mmWave massive MIMO channel estimation:Cl (·)denotes a learnable operator for sparse feature compression using CNNs,and l (·)denotes the corresponding inverse operator for decompression.

For a certain receive antenna,i.e.a sub-channel in the MIMO transmission system,the received frequency-domain OFDM data blockcan be represented as

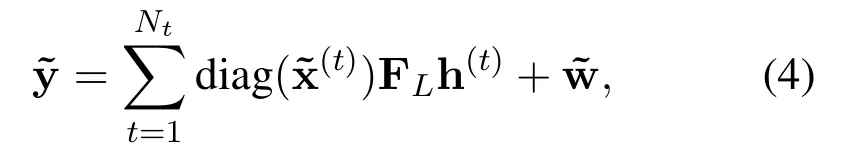
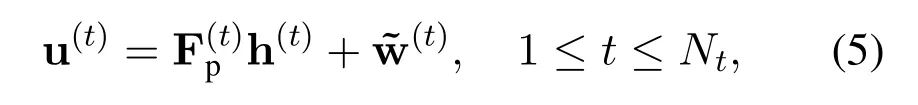
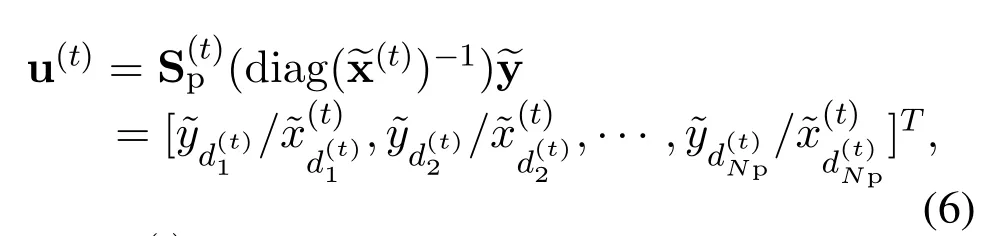
By stacking the CIR vectors of all the transmit antennasinto a single long vector,the deep CNN network can be trained to exploit the inherent spatial correlation among the mmWave massive MIMO channels.This is because one of the most important advantages of CNN is that a convolutional layer uses the same convolution kernel,i.e.parameter sharing,for the data at different spatial locations to extract a higher-level common feature,such as in image processing and pattern recognition applications[31].Then the stacked MIMO CIR vector is given by

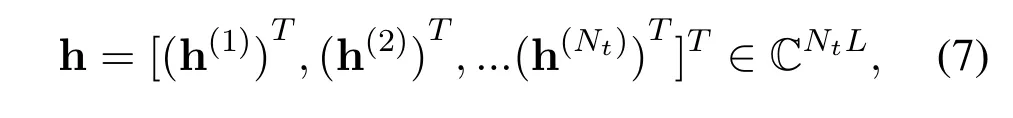
Consequently,the problem of sparse MIMO channel recovery can be formulated as

Due to the spatial correlation of the mmWave massive MIMO system,i.e.the spatial distance between different transmit antennas is much smaller than the propagation distance between the transmitter and the receiver,the CIR vectors of different transmit-receive antenna pairs share a sparse common support[7].More explicitly,the spatial correlation can be explained by the following formula as,

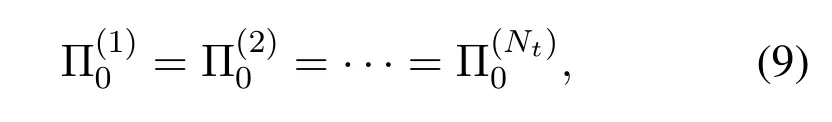
Although the proposed method is presented using a fully digital MIMO structure in this paper,it is also suitable for hybrid precoding structures[32–34],where the measurement model of the sparse MIMO channels can be built up in a way similar to the modeling given by(5)through(8),and the spatial correlation can be exploited to refine the support estimation,too.

IV.PROPOSEDDEEPCNN-BASED MMWAVE MASSIVE MIMO CHANNEL ESTIMATION SCHEME

In this section,the novel deep CNN-based mmWave massive MIMO channel estimation scheme is proposed.The CNN-based scheme is devised based on the classical iterative sparse recovery algorithm of ISTA.Using the ISTA algorithm,the original unknown signal x can be recovered from the measurement vector y=Ax through the iterations given by

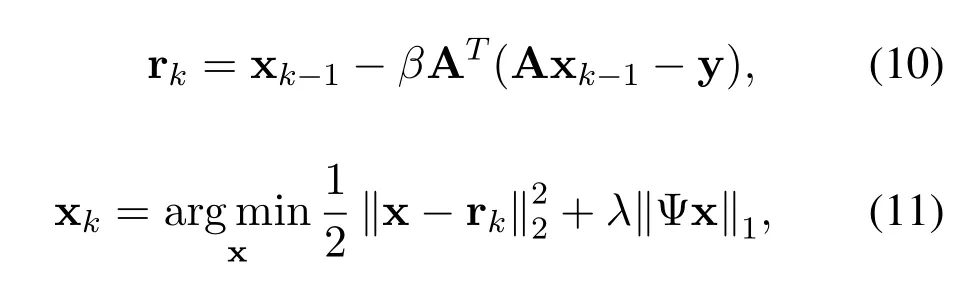
wherekis the iteration index andβis the stepsize.rkdenotes an intermediate proxy of xk,which is updated using the gradient descent of the squared estimation errorThe sparse solution of x can be obtained by minimizing the?1-norm of its sparse representation Ψx using the sparse basis Ψ,andλis a weighting parameter indicating the weight of sparsity on the minimization problem in(11).

In this work,a deep CNN-based sparse recovery network is devised to infer the mmWave massive MIMO channels,which only requires one forward propagation in the practical channel inference phase.The deep CNN network has a large fitting capacity and the sparse features can be effectively extracted to further improve the channel estimation accuracy.

The proposed network structure is illustrated in Figure 2,which consists ofNLidentical cascaded layers.A learnable operator denoted byC(·),which is composed of two convolutional(Conv)layers separated by a rectified linear unit(ReLU),is adopted for sparse representation and sparse feature compression,playing the role of the conventional sparse basis Ψ.Both the two Conv layers inC(·)haveNffeature maps,respectively.Thus,the ability to extract sparse features is greatly improved and the capacity of the network to fit different mappings is substantially extended through using CNNs.

Utilizing the CNN-based operatorC(·)for sparse regularization instead of the?1-norm‖Ψx‖1,the classical optimization problem in(11)can be transferred into a deep network with much better sparse feature extraction capability.Specifically,for thel-th layer of the network,given the stacked received measurement vector u and the observation matrix Φ,the stacked MIMO CIR vector estimated by thel-th layer denoted bycan be estimated by

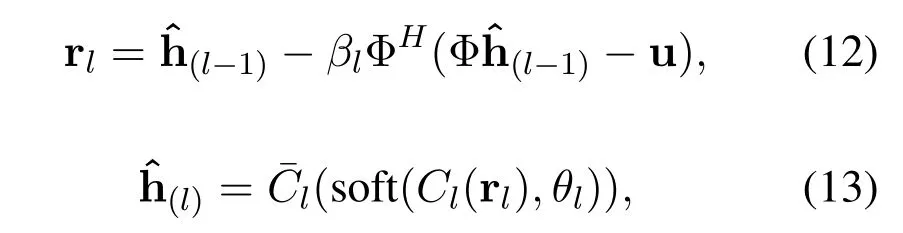
where soft(v;θ)is thesoft thresholdfunction,with soft(v;θ)=0,|v| ≤θ,and soft(v;θ)=sign(v)·is the corresponding inverse operator ofCl(·).Note that the learnable parameters up to layer-lin the network in Figure 2 can be aggregated into a setwhich contains the network weights and parameters associated with all thellayers.It can be learnt and optimized using back-propagation and gradient descent during training.

The training process is described in Algorithm 1,where the network is trained layer-by-layer in a sequential manner.The whole training process is composed of some number of stages indexed byl,andlis increasing sequentially during training.Specifically,in a certain stagel,the current network containsllayers and a corresponding current loss functionLl(Θl)is formulated for thisl-layers network with the parameter set Θl.The number of layers in the network is indicated byl,which should be increased as long as the current loss functionLl(Θl)is still decreasing with the increase ofl.When the loss function does not decrease withlany more,the final number of layersNLcan be determined,i.e.NL=l ?1.The reason is that at this time the halting condition is met,i.e.Ll(Θl)≥Ll?1(Θl?1),so the network withl ?1 layers in the previous stage is the one with the minimum training loss.

The current loss functionLl(Θl)for thel-layers network is composed of two parts:the normalized mean square error contributed by the channel estimation outputof thellayers,and the regularization term to impose symmetry constraints on the operator pairsCi(·)andHence,the loss function of layer-l Ll(Θl)is given by

whereδis the penalty parameter for the symmetric constraints regularization.The parameter setfor thel-layers network is learnt through minimizing the loss functionLl(Θl)over the training setLike the procedures in[19],the complex numbers are divided into real and imaginary parts,and trained separately in two networks with the same structure as shown in Figure 2.Then the output of the two networks are combined to form the estimated channel vector in complex numbers.

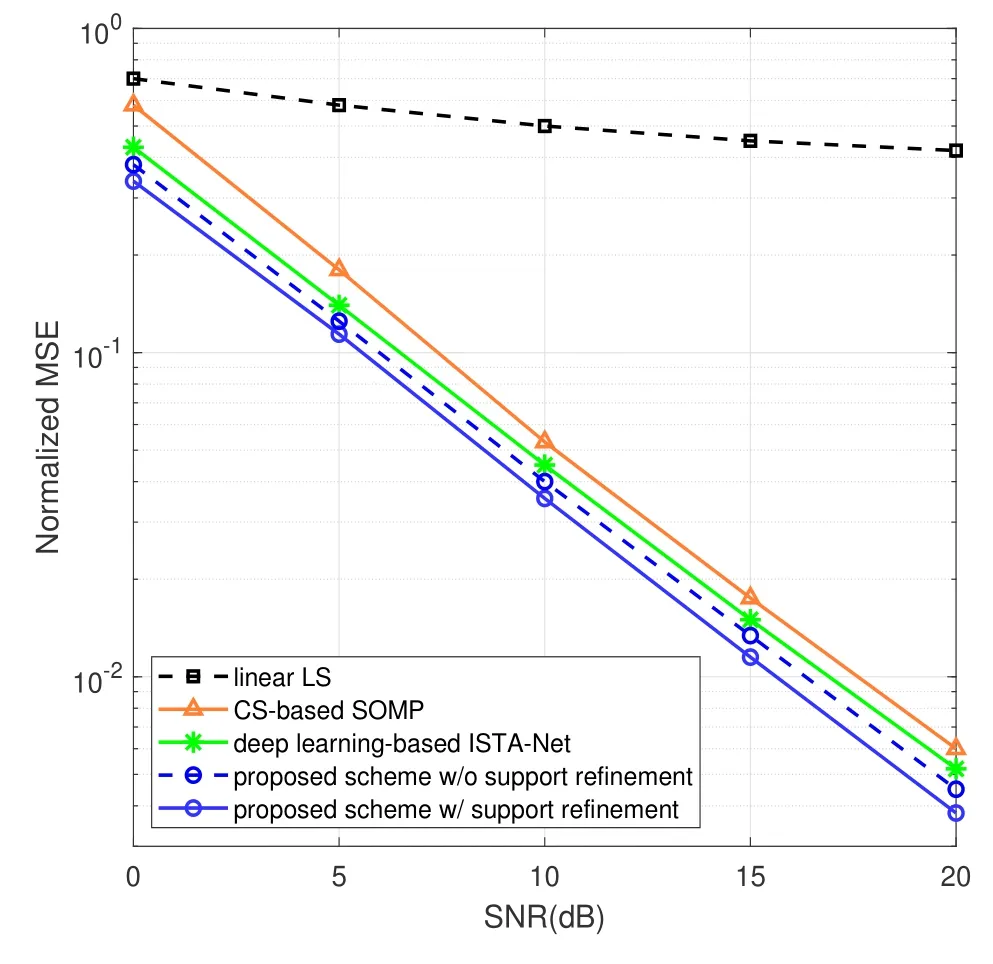
Figure 3.NMSE performance of mmWave massive MIMO channel estimation with respect to SNR.

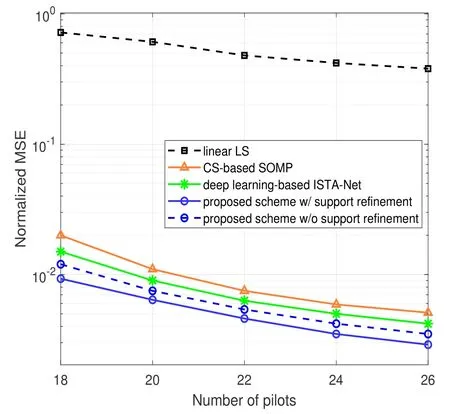
Figure 4.NMSE performance of mmWave massive MIMO channel estimation with respect to the number of pilots Np.

After the network has been well trained,the mmWave massive MIMO channels can be estimated accurately in the inference phase.First,the estimated stacked MIMO CIR vectorcan be obtained through the trained network with the learned parameters ΘNL.The estimated CIR vectorfor thet-th transmit antenna can be extracted from the correspondingt-th length-Lsub-vector of the estimated stacked MIMO CIR vectoras given by

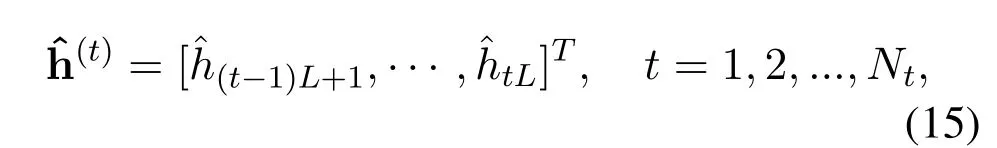
Algorithm 1.Deep CNN-Based Sparse Channel Estimation for mmWave Massive MIMO Systems.Input:Training set with size D:{ud,hdtrue}Dd=1 Initialization:1:h(0) ←0,l ←1 Iterations:2:repeat 3:Compute intermediate proxy rl based on(12)4:Generate the sparse stacked MIMO CIR vector h(l)based on(13)5:Calculate current loss function Ll(Θl)based on(14)and update current network parameters Θl=βi,θi,Ci(·), Ci(·)l i=1 through gradient descent and back-propagation over the training set{ud,hdtrue}Dd=1.6:Increase the number of network layers l ←l+1 7:until loss function does NOT decrease,i.e.Ll(Θl)≥Ll?1(Θl?1)8:Set the final number of network layers as NL ←l ?1 Output:Learned parameters ΘNL=βi,θi,Ci(·), Ci(·)NL i=1

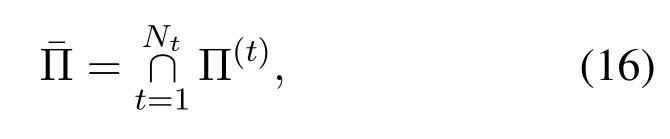
where Π(t)is the support offor thet-th transmit antenna.Finally,the corresponding refined CIR vectorfor thet-th transmit antenna based on the spatial correlation can be obtained by solving the least squares(LS)problem derived from(5)as given by

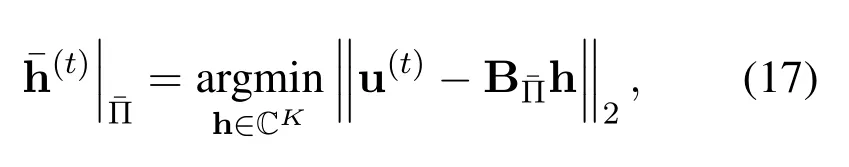
V.SIMULATION RESULTS

The performance of the proposed deep CNN-based sparse channel estimation scheme is evaluated by simulations.The conventional LS-based channel estimation method with linear interpolation[35]and the CSbased algorithm of simultaneous orthogonal matching pursuit(SOMP)[8],are evaluated for comparison.As a deep learning based benchmark,the state-of-the-art method of ISTA-Net[13]is also evaluated.The simulation parameters are configured in a mmWave massive MIMO system with the carrier frequencyfc=30 GHz andNt=Nr=64 antennas.The length of the OFDM data block length and the CP isN=4096 andM=256,respectively.The maximum channel length is set asL=256[26,36],which is the same as the CP length.It is a conservative maximum range of the possible CIR delay spreads generated according to the statistical channel distribution[26,36].Then,the CP length is sufficiently large to cover most of the CIR delay spreads to avoid inter-block interference.The actual sparsity level of the CIR vector is conservatively assumed to beK=12,which denotes the number of dominant CIR taps with much greater amplitude than the other small-scale nonzero taps in the parametric sparse channel model[26].The number of pilots adopted for channel measurements is set asNp=25.The SNR denoted byγused in the simulations is calculated byγ=Pr/σ2,wherePrdenotes the power of the received signal,andσ2denotes the power of the AWGNas in equation(4).

Figure 3 presents the NMSE performance of channel estimation in a mmWave massive MIMO system with multipath fading.It can be noted from Figure 3 that,the proposed deep CNN-based scheme outperforms the LS-based method significantly,since the number of available pilots is much smaller than the channel length,making it an underdetermined problem that LS cannot tackle but the proposed scheme can solve well.An NMSE gain of 2.0 dB over the CS-based method at the NMSE of 10?2is achieved by the proposed deep CNN-based scheme,validating the high accuracy of the proposed scheme.The proposed scheme outperforms the deep learning-based algorithm of ISTA-Net by 1.3 dB,which indicates that the proposed network has been optimized for mmWave massive MIMO channel estimation.Moreover,the gap between the proposed scheme with and without support refinement is about 0.8 dB,which verifies that the spatial correlation is fully exploited by the proposed support refinement method given in(16).

The channel estimation performance with respect to the number of available pilotsNpadopted for channel measurements is reported in Figure 4 at the SNR of 20 dB.It can be observed from Figure 4 that,the proposed deep CNN-based scheme can achieve better accuracy compared with the existing CS and deep learningbased algorithms using the same number of pilots.Meanwhile,the proposed scheme requires much less pilots for channel estimation than the benchmarks to reach the same target accuracy,which saves the subcarrier resource and improves the spectrum efficiency greatly.Besides,the proposed method with support refinement requires much less pilots than that without support refinement,which validates the benefits of utilizing the spatial correlation.

VI.CONCLUSION

In this work,a novel deep CNN-based mmWave massive MIMO channel estimation scheme has been proposed.By exploiting the CNN-based sparse recovery network,the mmWave massive MIMO channel is estimated with higher accuracy and spectrum efficiency than state-of-the-art methods.Simulation results verify that the proposed scheme can significantly improve the accuracy of mmWave massive MIMO channel estimation,especially in case of low SNR or insufficient measurement data,i.e.frequency-domain pilots,compared with the conventional LS-based method and the state-of-the-art CS-based and deep learning-based methods.The proposed deep CNN-based sparse recovery framework is promising to be widely applied in various mmWave massive MIMO scenarios,including indoor mmWave systems and outdoor mobility scenarios.

ACKNOWLEDGEMENT

This work is supported in part by the National Natural Science Foundation of China under grants 61901403,61971366 and 61971365,in part by the Youth Innovation Fund of Xiamen under grant 3502Z20206039,and in part by the Natural Science Foundation of Fujian Province of China under grant 2019J05001.