Jiangtao Li,Xu Bao,Wence Zhang

School of Computer Science and Communication Engineering,Jiangsu University,Zhenjiang 212013,China

Abstract:Driven by the continuous penetration of high data rate services and applications,a large amount of unregulated visible light spectrum is used for communication to fully meet the needs of 6th generation(6G)mobile technologies.Visible light communication(VLC)faces many challenges as a solution that complements existing radio frequency(RF)networks.This paper studies the optimal configuration of LEDs in indoor environments under the constraints of illumination and quality of experience(QoE).Based on the Voronoi tessellation(VT)and centroidal Voronoi tessellation(CVT)theory,combined with the Lloyd’s algorithm,we propose two approaches for optimizing LED deployments to meet the illumination and QoE requirements of all users.Focusing on(i)the minimization of the number of LEDs to be installed in order to meet illumination and average QoE constraints,and(ii)the maximization of the average QoE of users to be served with a fixed number of LEDs.Monte Carlo simulations are carried out for different user distribution compared with hexagonal,square and VT deployment.The simulation results illustrate that under the same conditions,the proposed deployment approach can provide less LEDs and achieve better QoE performance.

Keywords:visible light communication;lightemitting diodes;centroidal Voronoi tessellation;quality of experience;optimal deployment

I.INTRODUCTION

Visible light communication(VLC)utilizes the offthe-shelf Light-emitting diode(LED)as transmitters to emit the information signals and simultaneously provide the indoor illuminations.It has been a hot research topic recently because it can offload data traffic from existing wireless communication networks[1].In the future 6G short-range communication applications and mobile communication networks,VLC will play an important role in gigabit wireless networks underwater,cellular vehicle to everything(C-V2X),THz communication and light-based IoT(Internet of Things)[2,3].These very promising applications open new areas of research for 6G.VLC has some unique advantages compared with the radio frequency(RF)network,e.g.,no health risk,low cost,licensedfree-bandwidth,etc,[4–6].However,due to the lineof-signal(LoS)propagation of the visible light,one LED has a limited coverage area.Hence,multiple LEDs are needed to cover a room,while the indoor illumination quality and data throughput should be guaranteed by deploying LED carefully.

In the modern mobile communication network,small cell concept has been proved to be an efficient way to increase network throughput.Haas borrowed this idea and proposed the atto-cell in indoor VLC network[7].In the atto-cell,each LED is regarded as an optical access point(OAP)and serves users within its coverage area.Although more OAPs can provide the possibilities for accommodating more users and the satisfied illumination,inter-cell interference(ICI)will be increased to degrade the performance.Hence,the deployment of LEDs should be considered by using the appropriate number of atto-cells.

Usually in an indoor environment,the LED deployment schemes are based on the fixed and predefined LED locations,or assume a specific LED distribution and provide coverage analysis.Chen et al.in[8]studied square and hexagon LED deployment schemes based on geometric features,and analyzed the coverage by considering both coverage and interference factors.Chen and Haas[9]studied hexagon,square,poisson point process(PPP)and hard-core point process(HCPP)LED deployments.In[10],Shaima et al.used four different types of LED deployment,these LEDs are placed as diagonal line,horizontal central line,horizontal and vertical line and both diagonal line.In[11],Shashikant et al.proposed different hexagonal LED deployment schemes of VLC nodes for various indoor scenarios.These LED deployments correspond to different interference and overlap requirements between cells.In[12],Rui Guan et al.proposed the single-LED-based and array-LED-based deployment schemes,and in this paper,particle swarm optimization(PSO)was used to minimize the average shutdown area rate to obtain the best LED configuration.However,the above research did not consider user distributions in a room well.Under different scenarios,it may be different and not uniform.When the spatial distributions of LEDs and users are independent,the desired performance may not be achieved.Considering the non-uniform distribution of users,the optimal LED deployments should be adapted to users.

In contrast to the aforementioned schemes,Dastgheib[13]considered the stochastic behavior of mobile users in terms of their stationary distribution in the optimization of LED deployment.Knowledge of the users’ stochastic behavior helps to avoid unnecessarily spread LED light,which results in higher average throughput.Furthermore,an optimized deployment scheme considering a user random waypoint(RWP)model was proposed in[14],as the users continue to move,the distribution of the position of users approaches a stationary distribution.RWP model conforms to the user’s behavior habits in the VLC scenario,and is more conducive to optimizing LED deployment.Vegni and Biagi[15]defined the system model that allows to compute the probability density function(pdf)per user in a given indoor scenario.The pdf depends on the specific environment and user’s position.And[15]presented two techniques for optimal LED deployment,subject to both outage and illumination constraints.However,the above research did not illustrate the relationship between the users and the LEDs from the perspective of the distance.In fact,the distance between the users and the LEDs has a huge impact on the system performance.Given user distribution,we prefer that the average distance between LEDs and users should be minimized.

It is also important to find the appropriate metric to assess the performances of the LED deployment.In[15],Vegni and Biagi use the outage probability as an indicator to evaluate the performances of LED deployment.Stefan and Haas took area spectrum efficiency(ASE)as an indicator to evaluate LED deployment performances in[16].However,the above metrics cannot perceive the overall system performance from the user’s perspective.

In this paper,we utilize quality of experience(QoE)as a metric for evaluating the system performance and propose a new LED deployment that is adapted to the users’spatial distributions.The main contributions of this paper can be summarized as follows.

1.We proposed two techniques based on Lloyd algorithm,i.e.,Number-of-LEDs-minimizationbased LED deployment and QoE-maximizationbased LED deployment,which can solve the two proposed optimization problems,i.e.minimization of the number of LEDs and maximization of the average QoE of all users.The two optimization problems are transformed into the problem of minimizing the horizontal distance between LEDs and users in the cell.

2.Through the analysis of optimization problems,we utilize CVT to generate the optimized LED deployment,which can ensure the minimum distance between the LED and the associated users in each cell,and obtain better QoE and illumination quality.More importantly,CVT deployment can be adapted to different user distributions.

3.As a comparison of CVT deployment,we set up three LED deployments of hexagon,square and Voronoi tessellation(VT),which are simulated under uniform,Gaussian and PPP user distributions.CVT deployment is optimal in terms of satisfying the requirements of minimum number of LEDs,illumination quality and QoE performance.

The remainder the paper is organized as follows.The system model and problem formulation are introduced in Section II and Section III.In Section IV,we propse a detailed description of the methodology.The performance evaluation is presented in Section V.Conclusions are given in Section VI.

II.SYSTEM MODEL

Figure 1a illustrates the downlink configuration of an indoor VLC system,whose tridimensional dimensions aredX,dYanddZ[m].The VLC network consists of multiple LEDs that mounted on the ceiling.The users are equipped with the photodiodes(PDs)as the receivers to detect the VLC signal[17].The transmitter in our model uses a Lambertian optical source,of which the brightness to an observer is the same regardless of the observers angle of view[18].The users scatter randomly in room.

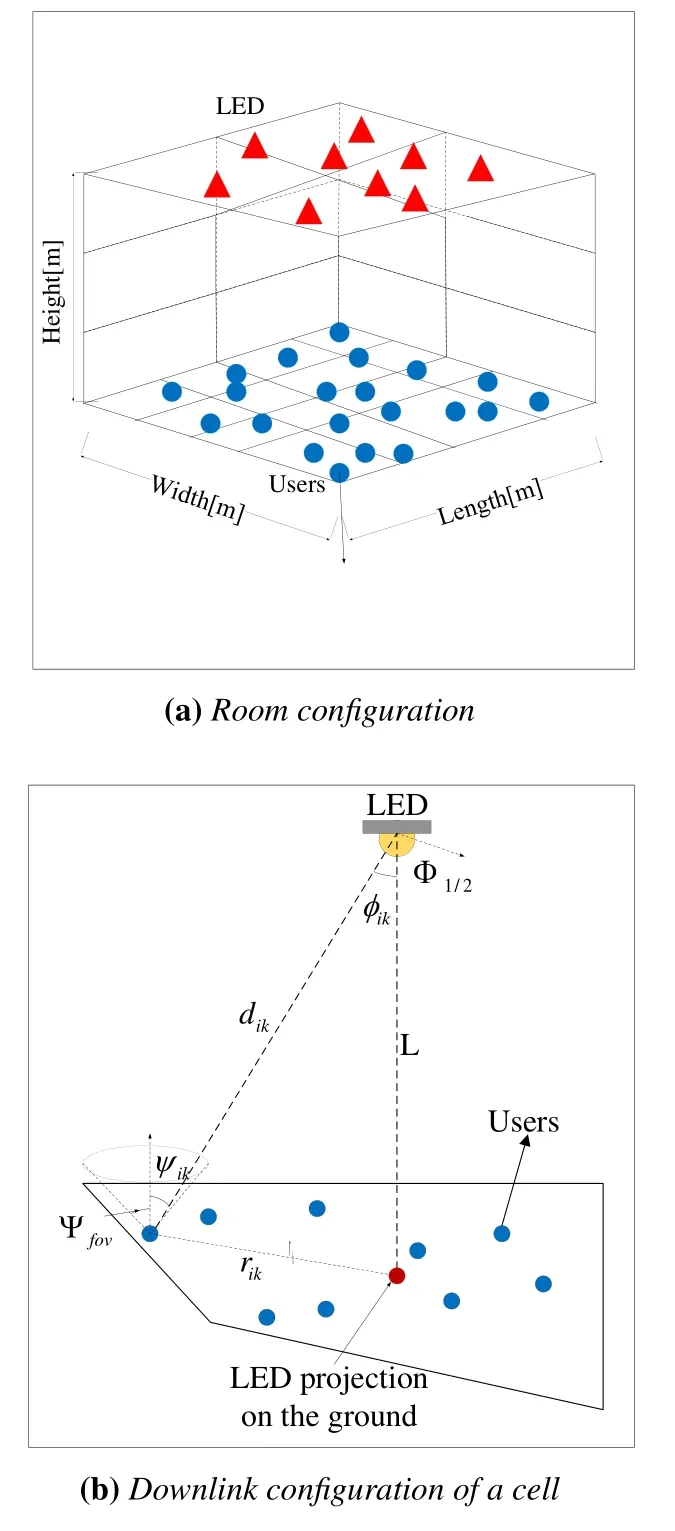
Figure 1.Red triangles represent LEDs and blue dots represent users,each LED provide illumination/connectivity service for users.

2.1 Optical Channel Characteristics

As shown in Figure 1b,the vertical distance between the receiver plane and the LED transmitter isL,which is a constant in this paper.dikis the Euclidean distance between thei-th LED and thek-th user,which is given bywhererikdenotes the horizontal distance between the LED with locationand the user with locationit can be expressed asAt thek-th user,the angle of irradiance and the angle of incidence are denoted byφikandψik,respectively.The direct current(DC)channel gain of the line of sight(LOS)link between thei-th LED and thek-th user,given by[19]

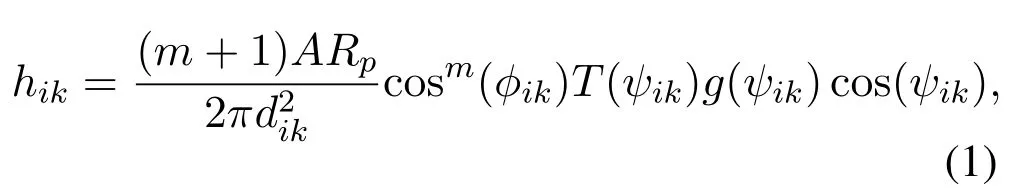
wheremis the order of Lambertian index,depending on the semi-angleφ1/2at half-illuminance of the LED,which is given bym=?1/log2(cosφ1/2),Ψfovdenotes the field-of-view(FOV)of a receiver,Adenotes the detection area of the PD,Rpdenotes the responsivity of the PD,T(ψik)represents the gain of the optical filter used at thek-th user,andg(ψik)represents the gain of optical concentrator,given by[19]:

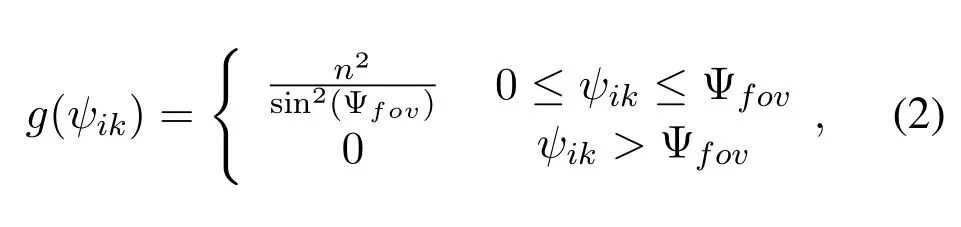
wherenis the reflective index of the optical concentrator used at the receiver front-end.nis typically valued between 1 and 2.Therefore,hikcan be represented as a function of thek-th user and thei-th LED position,given by

2.2 Quality of Experience

QoE is a method to evaluate the overall performance of the network from user’s perspective,which directly reflects users’approval degree of services.QoE can be obtained by using the mean opinion score(MOS)of data traffic[20].Compared with QoS,QoE has different expressions for different services[21,22].This paper mainly considers non-real-time traffic such as file transfer web browsing,and defines the corresponding QoE function as the increasing function of throughputRis given asR=Blog(1+SNR)[23],whereSNR=P|hik|2/N0B,B[Hz]is the available bandwidth,P[W]is the transmitted power,hikis the DC channel response,N0[W/Hz]is the noise power spectral density(Noise PSD).The QoE function is defined as:QoE=b1log(b2R),whereb1andb2can be determined by the required maximal and minimal throughputs[23],which are assumed to be 70 Mbps and 2 Mbps in this paper,respectively.And the resulting parameters are set asb1=0.6476 andb2=0.7503.Combined with Eq.(3),we can get the relationship among

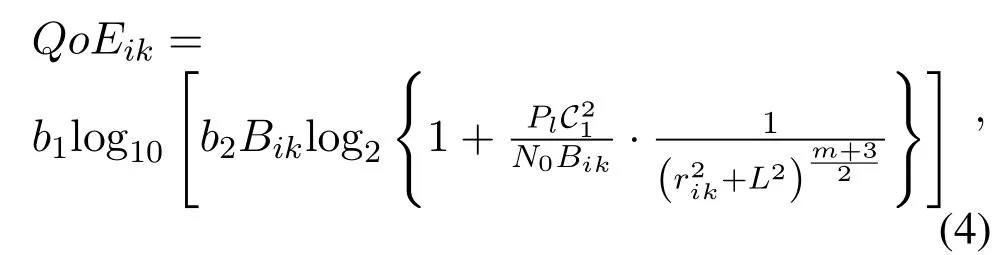
Hence,we can conclude thatQoEikincreases as the horizontal distance between user and LED decreases.

2.3 Illumination of LED Lighting

The illuminance is the most significant parameter when characterizing white-LEDs for illumination purposes.From radiation spectrump(λ)[W/m],one can obtain the luminous flux Φ(lm),of the source by evaluating

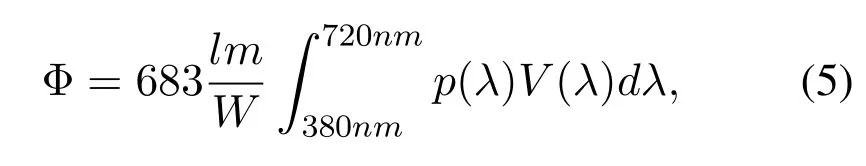
whereV(λ)denotes the eye sensitivity function[24,25].The luminous flux is the optical power of the source as perceived by the human eye.Relevant optical source parameters for data transmission are its radiant power and modulation bandwidth.The source optical powerP[W](radiant flux)is given asThe parameter of interest for us is the illuminance,E(lx),which expresses the brightness of the illuminated surface.According to[24],it is defined as luminous flux per unit area,E=?Φ/?A=I(θ)/dik2,and depends on the source luminous intensityI(θ)[cd],in the directionθ.Eaccounts for the radiation pattern of the light source and the distance to the illuminated surface,dik(see Figure 1b).Assuming a Lambertian radiation pattern,the horizontal illuminance can be calculated as[25]:

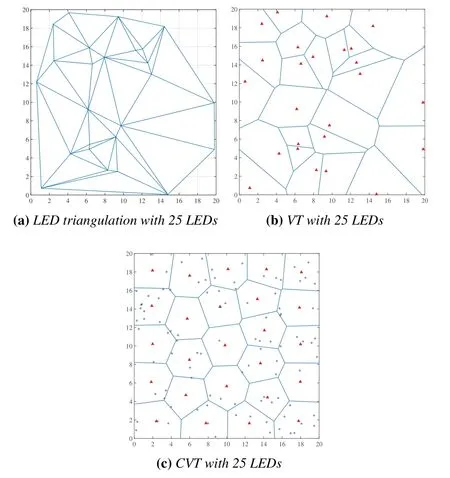
Figure 2.The procedure for generating CVT with 25 LEDs.

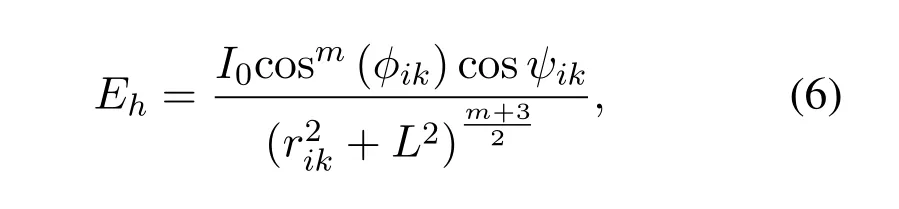
whereI0=I(Φ=0)=(m+1)φ/2πis the maximal luminous intensity[25].Therefore,the horizontal illuminance for thek-th user can be expressed as

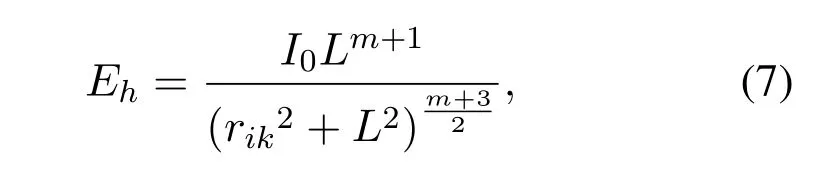
Analogous to Eq.(3)and Eq.(4),the performance of horizontal illuminationEhdepends on the horizontal distance between user and LED.

III.PROBLEM FORMULATION

In this section,we investigate the optimal deployment of LEDs by proposing two problems optimization,focusing on(i)the minimization of the number of LEDs that meet the users’ QoE constraints and the indoor illumination quality,and(ii)the maximization of average QoE under the satisfactory illumination quality.In order to design the generalized LED deployment algorithm,the inter-cell interferences are assumed to be totally eliminated by using the scheduling algorithm with considering the user fairness[26].The edge user between the adjacent cells are also guaranteed to have a satisfied QoE value.Nonetheless,excessive number of LEDs may still induce frequent hotizontal handovers[27].Horizontal handovers still bring a lot of performance losses,such as additional time delay and a drop in transmission rate.Therefore,it makes sense for our optimization purpose to reduce the number of cells.

3.1 Number-of-LEDs-minimization-based LED Deployment

Having too few LEDs leads to share the resource among users and results in data rate reduction.On the other hand,numerous LEDs may induce frequent handovers or serve inter-cell interference.

Hence,we try to solve the following problem(A):

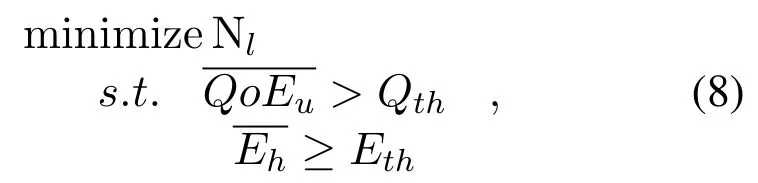
that is the minimization of the number of LEDsNl,subject to(i)the average QoE of all usersis at least equal to or higher than a given thresholdQth,(ii)the horizontal illuminanceis at least equal to or higher than a given thresholdfor the illumination in the room.Thecan be expressed as

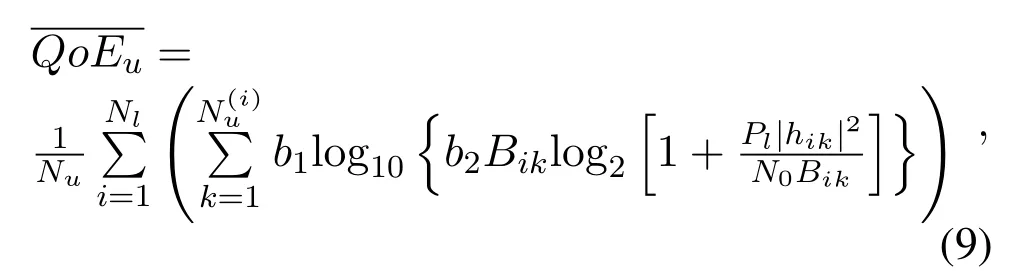
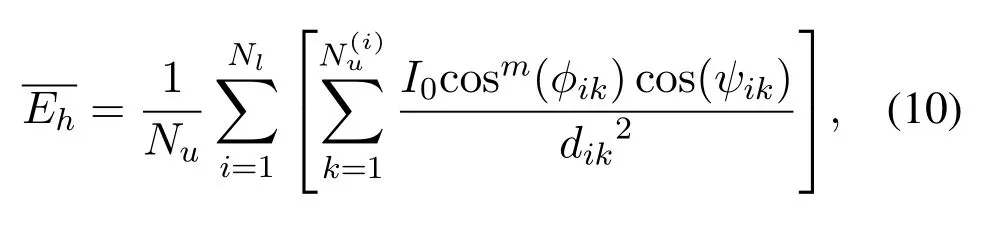
Simultaneously,the constraints of the optimization problem(A)can be transformed into the following expressions.

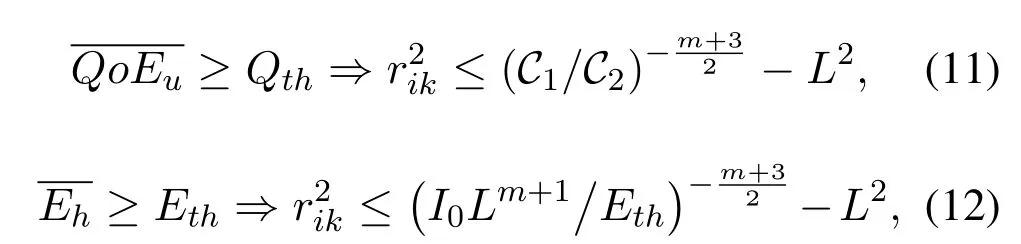
Therefore,the constraints of problem(A)should be

3.2 QoE-maximization-based LED Deployment

The second problem we tackle is the optimal LEDs deployment in the room by considering the constrains(i)satisfactory illuminance requirement,(ii)the fixed number of LEDs.We try to find the optimal LEDs deployment so as to maximize theSpecifically,we can formalize the problem(B)as follows:

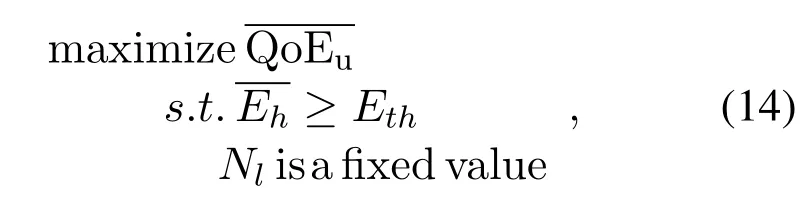
According to Eq.(4)and Eq.(9),can be expressed as a function of the horizontal distance between users and LEDs.Furthermore,maximizingcan be equivalent to minimizing the horizontal distance between users and LEDs,and the horizontal illuminanceis analogous to the previous problem.Therefore,the constraint is similar to Eq.(13).

IV.METHODOLOGY

4.1 Modeling LED Deployment Optimization by Centroidal Voronoi Tessellation

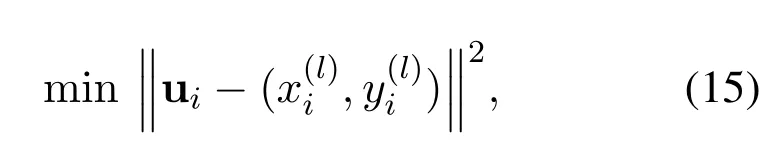
where‖·‖denotes Euclidean distance.According to Eq.(15),the user’s access strategy can be set to proximity access,i.e.,the user accepts the service of the nearest LED,it can be expressed as

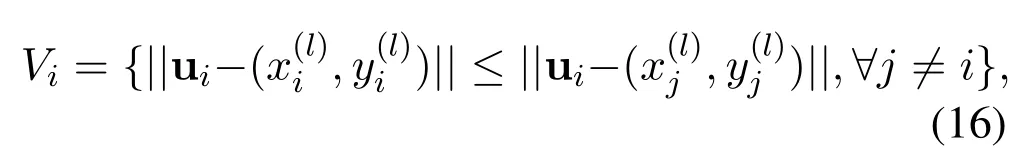
Videnotes i-th cell.If all cellsin the room meet Eq.(16),the setis a Voronoi tessellation or Voronoi diagram,and eachViis referred to as the VT corresponding toi-th LED[28].

Considering the whole room,Nlcells and user spatial distributions densityρ(u).The optimization problem can be converted to minimize the following expression.

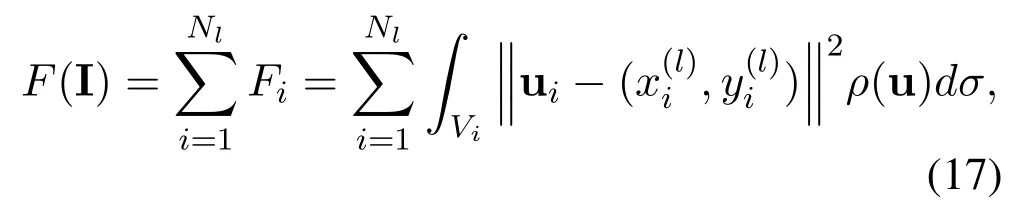
F(I)represents the cost function for users to obtain LED services[29].Define

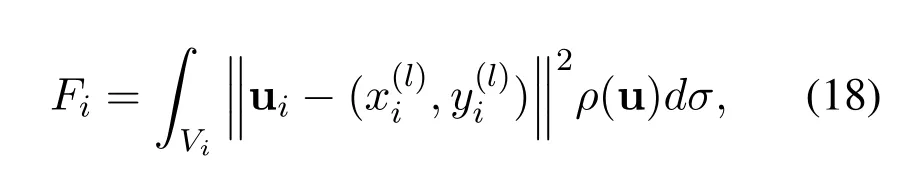
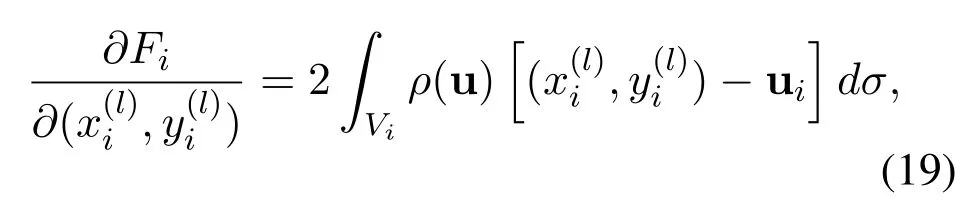
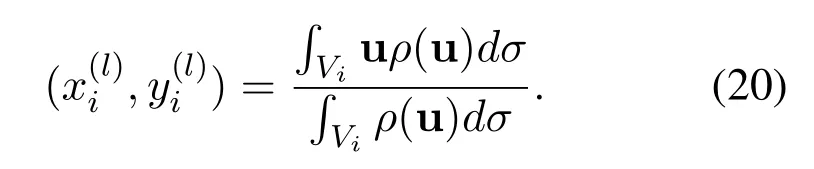
4.2 Construction of CVT

We use Lloyd’s method to construct CVT[31],each cell and LED are considered independent.First,VT is generated by the locations of LEDs.Then fix the VT and move LEDs to the centroidal of each cell,and update them alternately.The following Algorithm 1 is the process for generating the CVT.

1.Before generating CVT,VT should be constructed.The construction of VT is only related to the locations of the LEDs.Let’s take 25 LEDs for example that shown in Figure 2a and Figure 2b,it shows the construction process of VT.Figure 2a represents delaunay triangular network generated by 25 LEDs in the room,it is constructed by triangulation method.Triangulation method first select a LED indoors arbitrarily,connect the nearest LED as the initial baseline,and select the LED closest to the baseline to form triangle,continue to construct triangles according to the sides of the triangle as new baselines until the delaunay triangular network is completed.Simultaneously,calculate the circumscribed circle centers of all triangles,and connect the circumscribed circle centers of adjacent triangles together to form the boundary of VT,if there are triangles without coedges triangles,make perpendicular bisector on the sides.As shown in Figure 2b,when all triangles are iterated,VT construction is completed.

Algorithm 1.Lloyd’s algorithm for generating CVT.1:Input parameters:Nu,Nl,ρ(u),N=0 2:Output:CVT 3:Nu users are distributed in the room based on the probability density function ρ(u),denoted as u 4:The initial Nl LEDs are randomly distributed in the room,denoted as I 5:Initial selection:6:while F(n)?F(n?1) ≤ε do 7:Select an LED(x(l)i,y(l)i)8:Find the LED closest to(x(l)i,y(l)i)and connect to it as baseline,N=2 9:Connect the LED to the LEDs at both ends of the baseline to form the triangle,N=3 10:while N/=Nl do 11:Using the sides of the triangle as new baselines to find n LEDs closest to them 12:if n/=0 then 13:Updata:N=N +n and continue to generate triangles 14:else 15:Delaunay triangular network is completed and record each triangle t={ti}ki=1 16:end if 17:end while 18:Calculate the center of the circumscribed circle of each triangle,record c={ci}ki=1 19:for t do 20:Find the adjacent triangles t1i,t2i and t3i that are co-edge with the three sides of the current triangle ti 21:if t1i,t2i and t3i can be found then 22:Connect the center of the circumscribed circle of t1i,t2i,t3i and ti 23:else 24:Make a perpendicular bisector on the side where ti has no adjacent triangle 25:end if 26:end for 27:Calculate the centroidal of each cell,denoted as I'28:Update:I=I'29:Connect users to the closest LED according to the area divided by CVT 30:Calculate F(I)31:end while

2.After the construction of VT is completed.Calculating the centroid position I′of each cell according toρ(u)and the position uiof the user in the cell.Update the LED locations,i.e.,I=I′,and calculate the cost function according to Eq.(17).WhenFn ?Fn?1≤ε,it means that CVT has converged.Generally speaking,εis set to 8/(3Nl)[26],which means that the sum of the distances between all LEDs and the users has reached the minimum.As shown in Figure 2c,the CVT construction of 25 LEDs is complated.

4.3 LED Deployment Optimization

In order to achieve the minimum number of LEDs that meetandthe initial number of LEDsNlis set to 3,because that fewer than three LEDs cannot constitute a VT After generating CVT,if the number of LEDs can not meet the needs of all indoor users,the number of LEDs will be increased,until the constraints are satisfied.Finally we achieve the minimum number of LEDs.

Algorithm 2.CVT-LEDs minimization.1:Input parameters:Qth,Eth Nu,Nl 2:Output:Nmin l 3:Initial selection:4:while Nl≥3 do 5:Construct CVT according to Algorithm 1 6:Calculate QoEu andEh 7:if QoEu≥Qth and Eh≥Eth then 8:Output Nl 9:else 10:Update:Nl=Nl+1 11:end if 12:end while

The problem(B)can be solved by Algorithm 1 and Algorithm 2.We want to use a fixed number of LEDNlto obtain the maximum user average QoE that needs to meet the illumination conditions of the user,i.e.,Nlshould be greater than the minimum LED value that meets the illumination requirements of the users.The minimum number of LEDscan be obtained by Algorithm 2,only considering.Because CVT has ensured the smallest distance between users and LEDs through Algorithm 1.Finally,obtained is the maximum value.The process is in Algorithm 3.

Algorithm 3.CVT-QoE maximization.1:Input parameters:Eth Nu,Nl 2:Output:QoEu max 3:Initial selection:4:Calculate the minimum LED number Nmin lby algorithm 2 only considering the illuminance constraint Eth 5:When Nl≥Nminlis satisfied,construct CVT according to Algorithm 1 6:Calculate QoEu max

V.PERFORMANCE EVALUATION

In this section we provide numerical simulation results of the two approaches named as CVT-LEDs minimization and CVT-QoE maximization,to solve the optimization problem(A)and(B).The simulation scenario is constructed within a room of 20m×20m×3m(long,wide and height).As a comparison,VT deployment,hexagonal network deployment,square network deployment are simulated in this paper.In order to analyze the robustness of the algorithms,we investigate the effects of different user spatial distributions on the VLC system performances.In this paper,the locations of users follow 2-D homogeneous PPP with density of 6,Gaussian distribution with mean of 10 and standard deviation of 5 and uniform distribution,respectively.The total transmission power and bandwidth of every LED are assumed as 20W and 10MHz,respectively.We assume that the vertical distance of the VLC transmitter plane and the optical receiver plane is 2.5 meters.The detail simulation parameters are summarized in Table 1.

Table 1.Simulation parameters.

5.1 Users Distribution and LED Deployment

In optical Attocell networks,LEDs can be deployed in different ways to meet illumination and communication.Several types of LED deployments for optical attocell networks are considered and discussed below.

5.1.1 CVT Deployment

As shown in Figure 3a,based on Algorithm 1,CVT deployment is related to user distribution and meet the optimization requirements of problem(A)and problem(B).CVT deployment can be optimized by minimizing the distances between the LEDs and the users.It means that the locations of the LEDs can be adapted to the distribution of users.

5.1.2 VT Deployment

As shown in Figure 3b,LED and user distributions are independent of each other.That is to say,VT deployment cannot be adapted optimally to the user distribution.In this paper,the LED in VT deployment is uniform distributed indoors.

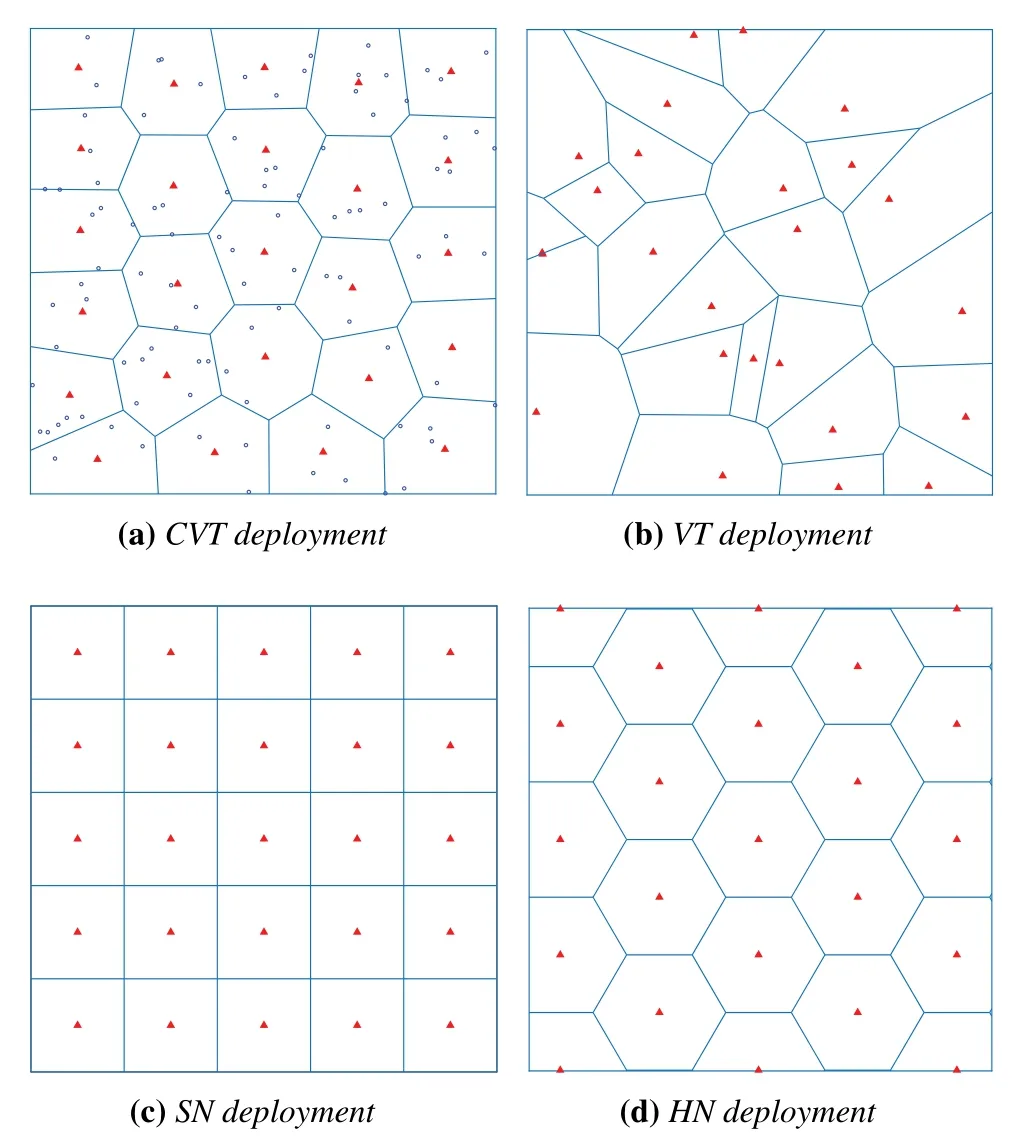
Figure 3.The red triangle in the figure represent the positions of LEDs,the blue circles represent the positions of the users.Blue lines represent the boundaries of cells.Only CVT deployment is related to user distribution,and the other three deployments are independent with user distribution.

5.1.3 Square Network Deployment(SN Deployment)

As shown in Figure 3c,LEDs are deployed so that the service area can be divided into square-shaped networks,which has been widely used in indoor scenes due to its advantages such as uniformity of illumination and simple design.However,this regular topology cannot be adapted to different user distributions,and the number of LEDs in this regular LED deployment is non-prime number..For example,the number of LEDs in square network deployment can be 9,16,25,36,49,etc.Once the user distribution has been changed,it cannot guarantee the stability of the VLC system.

5.1.4 Hexagonal Network Deployment(HN Deployment)

As shown in Figure 3d,similar to the SN deployment,HN deployment has the same advantages and disadvantages.We have considered the following LED numbers through different hexagonal radii,such as 14,23,30,33,42.

5.2 Number-of-LEDs-minimization-based LED Deployment

As shown in Table 2,we set up six sets of different QoE and illuminance constraints to obtain the LED deployment results of problem(A),and obtain the number of minimum LEDs under different conditions.

Table 2.Six sets of constraints.

Figure 4 demonstrates the minimum number of LEDs required for four deployments under different user distributions and constraints.CVT deployment outperforms the remaining schemes with the minimum fluctuation in differentQthconditions underEth=200lx and 400lx constraints.Note that CVT deployment should satisfy inequation Eq.(13),thus it can always be adapted to the user distribution as shown in Figure 5.The minimum LED number of the other three deployments are relatively larger,and it fluctuates greatly when the user distribution has been changed.In the process of constructing VT deployment,the LED distribution and the user distribution are independent of each other,therefore it cannot guarantee the minimum distance between LED and the associated users in each cell,which makes it difficult to achieve expected performance.

Figure 4.We set up six sets of constraints by setting different QoE and illuminance constraints to compare the performance of the four LED deployments,and through the constraints can observe the effect of QoE or illuminance on the number of LEDs under the same Eth or Qth .

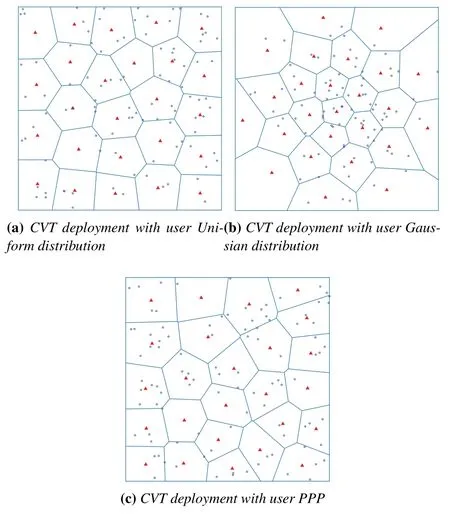
Figure 5.The red triangle and the blue circle indicate the location of the LEDs and users respectively.According to the principle of the CVT,the LEDs can adapt to the distribution of users,so that the LED deployment can minimize the distance between all LEDs and the associated users in each cell and improve the performance of the VLC system.

Besides,VT deployment requires more LEDs under the Gaussian and PPP distributions of users due to the LEDs are uniformly distributed.Compared with the other two user distributions,PPP can be regarded as the worst-case scenario with the maximum number of LED required due to the randomness locations of LEDs[9,32].The following simulations follow this principle.In addition,in HN and SN deployment,the LED location is fixed in advance,which cause the minimum number of LEDs under different user distributions to fluctuate greatly.As shown in Figure 6a and Figure 6b,since users are Gaussian distributed,most users locate in the middle of the room,as a result,the LEDs that distributed on the edge of the room cannot provide effective services for users.The performances of the minimum number of LEDs under the six sets of constraints are also compared in Figure 4.As shown in Figure 4a,under the condition ofEth=200lx,theQthrequirement increases from 3.5 to 4.5.In a scenario where users are uniformly distributed,the minimum LED number in HN and SN deployment can satisfy the requirement ofQth=4.5 providedQth=4 is met.The reason is that the number of LEDs in SN and HN deployment is restricted,the increasing number of LEDs in these two deployments must be able to maintain their regular topology.While in CVT deployment,the minimum LED number only increases by 5 to satisfyQthwhich is elevated from 3.5 to 4.5 and from 4 to 4.5.In the scenario where users are Gaussian distributed,the number of LEDs remains the same regardless ofQth=3.5 orQth=4 in SN and HN deployment since the regular topology provides the service margin withQth=3.5.In the scenario of users’PPP distribution,VT deployment performs the worst,because users are scattered and disordered more randomly while it cannot minimize the distance between users and LEDs and hence results in more LEDs.Figure 4b illustrates the minimum number of LEDs under the condition ofEth=400lx,theQthrequirements also increase from 3.5 to 4.5.It is found that ifQth=3.5 can be achieved in all LED deployments with a certain number of LEDs so doesQth=4.In other words,once the number of LEDs meets the condition ofEth=400lx,it can satisfyQth=4.in addition,for the condition ofQth=4.5,it can be observed that the number of LEDs required is slightly more than the number ofEth=400lx.Comparing Figure 4a and Figure 4b,we can conclude that CVT deployment performs the best among the four deployments,while SN and HN deployment require a larger number of LEDs in the Gaussian distribution scenario,and the performance of VT deployment has the worst performance except in Gaussian distribution scenarios,which requires the largest number of LEDs.

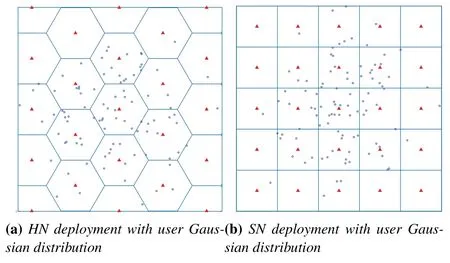
Figure 6.The LEDs Square network and hexagonal network deployments are fixed in advance,which lead to unstable performance of the VLC system if the user distribution is not uniform.When the user distribution is Gaussian,most users are located in the center of the room,which results in the four sides of the LEDs can not effectively provide services.

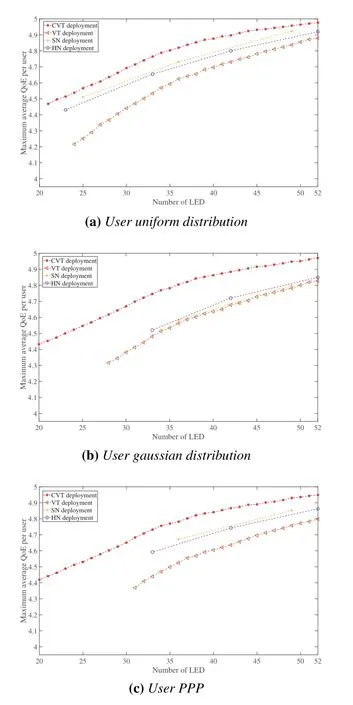
Figure 7.Comparison of maximum average QoE under Eth =400lx.

5.3 QoE-maximization-based LED Deployment

As for the optimization problem(B),we obtain the optimal LED deployment by maximizing the average QoE given a fixed LED number and an illumination constraints.The illumination level in this simulation is assumed to be 400lx according to the European lighting standard[24],the minimum number of LEDs required is different under different LED deployments and user distributions.As shown in Figure 7,we can easily find out that the average QoE obtained by CVT deployment is the highest,as well as the average QoE obtained by adopting the same number of LEDs.The reason has already been given in the result analysis of problem(A),both of which are because CVT deployment can be adapted to different user distribution.In the overall trend,the performance of VT deployment is the worst.As for the influences of the user distribution,the performance of VT deployment with uniform distribution is relative better compared to Gaussian or PPP user distribution.It is because that the LEDs in VT deployment are uniformly distributed,the average distance between the LEDs and the users can be relatively reduced.In Figure 7a and Figure 7b,the performance of SN and HN deployment is slightly better than VT deployment,because the LED positions in SN and HN deployment are restricted and arranged regularly,the average distances between the LEDs and the users are relative small with different user distributions compared to VT deployment.In Figure 7b,considering the Gaussian user distribution scenario,VT,SN and HN deployment have achieved similar performance,however,SN and HN deployment performed poorly when compared with the other two user distribution scenarios,this is because the LEDs in the middle of the room are not enough to serve the highly dense users in the middle,and it’s beyond the grasp of those LEDs which are located at the edge of the room.

VI.CONCLUSION

In this paper,we discussed and evaluated the optimal LED deployment scheme in indoor VLC network by taking QoE as the evaluation metric and considering the distribution of users.We proposed two approaches which based on Lloyd’s Algorithm that are adopted to solve the two optimization problems(i.e.,the minimization of the number of LEDs to be installed in order to meet illumination and average QoE constraints,and the maximization of the average QoE of users to be served with a fixed number of LEDs).These two optimization problems are transformed into the problem of minimizing the horizontal distance between the LED and the users in the cell.We proposed CVT that is used to optimize LED deployment.Through the simulation results obtained,the proposed CVT deployment can use a smaller number of LEDs and better QoE than other LED deployments,thereby improving the performance of the VLC system.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China(No.61772243);Jiangsu Provincial Key Research and Development Program(BE2018108);Six talent peak high level talent plan projects of Jiangsu Province(XYDXX-115).